子母管结构中海缆涡激振动特性研究

潘 盼，蔡炳余，谭爱林，郭朝阳，谢书鸿

(中天科技海缆有限公司，江苏 南通 226010)

子母管结构中海缆涡激振动特性研究

潘 盼，蔡炳余，谭爱林，郭朝阳，谢书鸿

(中天科技海缆有限公司，江苏 南通 226010)

采用流固耦合分析方法，对某海洋石油开采项目采用的子母管结构进行涡激振动特性研究，并与相同海缆在自由悬跨状态下振动特性进行比较。数值仿真结果显示，受母管影响，子母管中海缆由于涡街效应产生的升力振幅随时间变化不一致，而单根海缆升力幅值稳定；子母管中海缆产生的拖曳力高出单根海缆65%，振动幅值加大，并且沿整根海缆尾流中湍动能分布呈现随机性，导致水动力沿整根海缆分布不均匀。提取海缆升力与垂直水流方向振幅进行比较，发现涡激升力是导致垂直方向振动的主要原因。子母管中海缆在水流阻力和涡激升力共同作用下产生较大的位移和应变，应进一步调整夹具间距和剩余张力来减缓海缆疲劳损伤。

子母管；涡激振动；自由悬跨；流固耦合；湍流动能

随着陆上可用资源日益短缺和近海资源开发日益成熟，海上资源勘探、开发和利用正迅速向深海领域发展。作为勘探和输送海洋油气资源的海底电缆和柔性管道在布放过程中，若不能充分被沙土掩盖，便存在大量悬跨状态。波浪和洋流绕过悬跨段的海底电缆或管道时，在两侧周期性地脱落旋转方向相反、排列规则的双列线涡，即卡门涡街，使得结构表面在垂直于流动方向生成交变水动力，造成涡激振动。若振动频率与海缆或柔性管道的整数倍自振频率接近，便发生共振。涡激振动是造成海洋管道、海底电缆疲劳破坏的主要因素[1-3]。

为提高海洋油气田开发的经济效益，海洋技术人员开发了管束结构，将主管道和附属管道捆绑于一体，即子母管(piggy-back)，其中主管道用于输送碳氢化合物，附属管道或海缆用于传输化学试剂、电能或控制信号[4]，如图1(a)所示。

相对于单根海底管道，子母管周围流场和水动力特征分布更为复杂，大管和小管之间的相互干扰更增加了整体结构的设计、安装难度。近年来，许多学者对子母管水动力特性开展了广泛的理论分析和模型试验研究。Chung等[5]试验观察了深海管束结构中海缆绑捆方式对涡抑制能力的影响；Kalahatgi等[6]研究发现子管的存在使得母管拖曳力强度增加了50%～100%；Zang等[7-8]采用水槽试验和粒子图像测试技术研究了温流下子母管拖曳涡流抑制因素和涡激振动特性，并指出了尾流结构中涡强与子管振幅之间的联系；成小飞等[9]通过物理试验研究了子母管结构分别在规则波和不规则波作用下的水动力特性，并基于“等效直径法”分析得到了子母管各水动力系数。

依据科威特某海洋石油开采项目，提取子母管结构中关键结构参数如图1(b)所示，其中，海底与母管间隙e根据实际地理勘测设定，约为1.54 m。海缆与母管夹具间隔为4 m。

图1 子母管结构Fig. 1 Piggy-back structure

1 计算模型

为分析子母管在真实工作环境下的结构性能，采用MFX-ANSYS/CFX流固耦合计算方法，依据子母管结构的海洋环境实地勘察资料，提取10年回归期的波浪和洋流参数如表1所示，计算其在波流共同作用下的流场分布特征和涡激振动特性，并与单根海缆在相同海洋环境下的工作性态进行比较。

表1 环境参数Tab. 1 Environment parameters

1.1数值计算模型

母管相对刚度较大，在计算过程中被设定为刚体。海缆为双层铠装钢丝绞合结构，根据力学设计指标，提取等效弹性模量为7.59×1010N/m2。建立子母管中海缆有限元模型如图2(a)，图中海缆长度为12 m，对四处夹具位置截面节点进行全约束，模型考虑重力影响。子母管长方体流体域计算模型如图2(b)所示，设定尺寸约为12 m×20 m×80 m。整个计算域采用结构化网格划分方法，为了体现边界层黏性流动特征，对子母管附面层网格进行加密处理，第一层网格厚度Δy[10]由式(1)确定。

其中，L为特征长度，值为管的直径;y+为壁面无量纲量，值为1；Re为雷诺数;V为流体速度;υ为运动黏性系数。根据子母管所处海洋环境，Δy约为10-2mm，整个计算域网格单元为210万。

图2 子母管计算模型Fig. 2 Meshing model of piggy-back structure

1.2控制方程

子母管中海缆在水流作用下的涡激振动计算过程包括流场的非定常计算和结构的瞬态动力分析。海缆振动计算采用ANSYS中瞬态动力分析方法，流动介质采用CFX中Water模块。选用可压缩的连续方程和雷诺平均的N-S方程，采用二阶迎风后插方法，对整个计算域进行瞬态模拟，并使用动网格技术。在笛卡尔坐标系下，三维可压缩雷诺时均N-S方程：

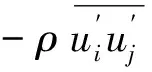
海缆在瞬态分析过程中，其结构动力学方程：

式中：Mg为质量矩阵；Cg为阻尼矩阵；Kg为刚度矩阵；Fg为利用CFD法计算得出的外表面流体压强分布。

海缆涡激振动计算过程中，结构和流场采用相同的时间步长，基于弱耦合求解方式，在每个时间步长内，先求解三维瞬态流场分布，再将流体载荷耦合至结构模型上，分析振动特性。湍流模型选取剪切应力运输模型(SST)，该模型整合了k-ε模型和k-ω模型的优势，充分利用了k-ω模型在低雷诺数时无需壁面函数的优势，而在主流区域内采用标准的k-ε模型，壁面了k-ω模型对来流的敏感型，模型表达式和参数见文献[11]。

1.3边界条件

在计算域上游入口位置，速度分布考虑波浪和洋流的共同影响。根据DNV设计规范[12]，波浪对海底管道位置处的流速采用线性波理论，洋流的速度分布需考虑海床边界层的影响，见式(5)：

图3 子母管高度处水流速度廓线分布Fig. 3 Current velocity profile around piggy-back structure

式中:V(zr)为参考高度处的速度，θc为洋流方向与管道方向夹角，通常取值为90°。计算域下游出口给定平均静压，子母管结构外表面及计算域底面设定为无滑移边界，计算域其余外表面设定为对称边界。

2 计算结果与分析

将表1工况下，海缆高度处合成水流速度输入计算域Inlet边界，其速度廓线分布如图3所示。由于海床边界层效应，此处水流降至0.31 m/s，而远离海床位置处合成水流速度约为0.75 m/s。设定时间步长为0.01 s，进行瞬态模拟，收敛准则选取计算域内所有控制体积的平均残差(RMS)，残差目标设定值为5.0×10-5。

由于海缆尾流中拖曳涡系影响其展向水动力分布，本文提取计算域整根海缆(12 m)上水动力随时间变化，即与水流方向垂直(Cross_line)升力和与水流方向平行(In_line)拖曳阻力，如图4所示。由图可见，受到母管影响，子母管结构中海缆水动力随时间呈现杂乱无章变化特征。相比于单独海缆状态下，子母管结构中海缆拖曳阻力振幅加大，最大峰值约为325 N，对应振幅约为40 N。而单独海缆在相同水流条件下最大拖曳阻力为200 N，对应振幅为5 N，由此，海缆在母管影响下，拖曳阻力增加了62.5%。子母管结构中海缆垂直水流方向升力在自身涡激励作用下，还受到母管的交替涡激影响，水动力峰值约为143 N，谷值约为-58 N，幅值为201 N，整个计算过程平均值为正值，起到提升海缆的效果。单独海缆的升力交替变化分布均匀，峰值为98 N，受到速度廓线影响，谷值为-93 N，幅值为191 N，与子母管中海缆升力幅值接近。与此同时，子母管结构中海缆拖曳阻力和升力交替频率接近，约为0.13 s。而单独海缆顺水流方向水动力交替频率约为0.07 s，垂直水流方向交替频率为0.15 s。

图4 海缆上水动力时程分布Fig. 4 Hydrodynamic variation with time along the cable

图5为子母管结构在17.71 s时沿展向各个截面流线分布图，各截面以管中心截面对称分布。由图可见，波浪和洋流合成水流流经母管后，在母管上下两侧形成速度增强区域，处于该位置的海缆生成了相对于单根海缆较高的水动力。从该12 m长子母管结构的各个截面可看到，母管后方生成的涡系具有较大的差别，涡系进而影响局部位置海缆的水动力特性，使得其沿展向分布呈不对称性，且偏差较大，在r=1 m、-1 m、5 m和-5 m截面，海缆顶部生成速度增强区，而在r=3 m和-3 m时，海缆底部生成速度增强区。各个截面对应的水动力参数见表2所示，其中，整根缆上的拖曳阻力分布大致相同，可见该方向的水动力主要是由水流阻力造成的。

图5 子母管各截面流线分布Fig. 5 Streamlines of different sections of the piggy-back structure

截面位置r/m135-1-3-5Cross＿line/N22．7854-25．252331．968225．8741-2．361127．4771In＿line/N27．065733．877828．755630．298828．743727．8650

图6为子母管结构中海缆和单根海缆在相同工况下，生成最大升力时尾流中湍流动能分布。湍流动能是流体力学中一个重要变量，是湍流强度的度量[13]，其表达式：

由图6可见，由于母管的影响，使得结构中海缆尾流中的湍流动能分布沿展向存在较大的差异，使得海缆整体水动力呈现不均匀的特征。而单根海缆，如图6(b)所示，由于不受外界干扰，其尾流中湍流动能呈现对称分布特征。

图6 海缆湍流动能分布Fig. 6 Turbulence kinetic energy distribution

图7为子母管结构中海缆中间截面受到升力和沿升力方向的位移时程变化，海缆在洋流和波浪联合作用下发生沿洋流方向和垂直方向的耦合振动。提取垂直方向位移变化可看出，海缆中间截面升力和位移变化在计算一段时间后，保持稳定状态，峰值大于谷值绝对值，海缆的振动频率与海缆升力保持一致，约为0.15 s。由于海缆自重，其向上振动最大位移值约为4.23 mm，向下振动最大位移值约为7.01 mm。由此可见，涡激水动升力是造成海缆竖向振动的首要原因。

图7 海缆中间截面升力和位移时程变化Fig. 7 Lift force and displacement of the middle section of cable

图8为海缆结构模型在第14.32 s和14.37 s时，受到涡激水动力发生位移形变示意图。由图8(a)，由于4个截面位置节点被全约束，其最大位移发生在约束截面中间位置，在14.32 s时刻，最大位移r=0 m处，约为10.54 mm，而在r=±4 m截面处，位移相对变化较小。0.05 s后，截面位移出现相反的情况，最大值发生在r=±4 m截面处，约为11.67 mm。

图8 海缆结构模型位移变化Fig. 8 The displacement of cable FEM model

图9为海缆在第14.32 s和14.37 s时，截面分别在r=0，±4 m处位移变化和周围流线分布示意图。与图8中海缆位移变化分布一致，在第14.32 s时，最大位移发生在海缆中间截面(r=0 m)，而在14.37 s时，位移发生最大位置为r=±4 m处。由图可见，海缆在发生上下振动的同时也伴随着顺着水流方向的位移。海缆截面一侧流体流速的增加，降低了该处的压强，迫使海缆向该处移动。在图9(b)中，r=0 m位置，海缆截面上下水流流速大致相同，因此位移表现不明显。涡街的形成带来海缆两侧交替变化的压强降，在水流阻力作用下，形成交替变化的振动。在该工况下，海缆被夹具约束的4 m长海缆中间截面出现了较大的振动位移，该振动位移势必带来较高频率变化的循环应力，因此应进一步调整子母管夹具间距，并增强其中海缆的铺设张力，以缓解疲劳损伤。

图9 海缆结构模型各截面位移和流线分布Fig. 9 Streamlines and displacement of each section of cable model

3 结 语

通过流固耦合分析方法，分析了子母管结构中海缆在洋流和波浪联合作用下的涡激振动特性，得到以下结论：

1) 在10年回归期的波浪与洋流条件作用下，22 m水深处子母管中12米长海缆水动力幅值变化呈现不稳定特性，而单根海缆在相同条件下，水动力幅值变化保持一致；

2) 受母管影响，海缆所在位置出现水流流速增强区域，使得该结构中海缆产生拖曳力值相对于相同条件下单根海缆高出65%，升力高出45.9%，并且升力峰值为143 N，而单根海缆为98 N；

3) 结构中海缆尾流中湍流动能分布沿展向存在较大的差异，使得海缆整体水动力呈现不均匀分布的特征；

4) 涡街的形成带来海缆两侧交替变化的压强降，伴随着水流拖曳力作用下，使得海缆形成交替变化的振动。应进一步调整夹具间距和海缆剩余张力，以缓解海缆疲劳损伤，提升使用寿命。

[1] Recommended Practice DNV-RP-F105, Free spanning pipelines[S]. 2006.

[2] YANG Bing, GAO Fuping, WU Yingxiang, et al. Experimental study on vortex-induced vibrations of submarine pipeline near seabed boundary in ocean currents[J]. China Ocean Engineering, 2006,20(1):113-121.

[3] CHEN Weimin, ZHENG Zhongqin, LI Min. Multi-mode vortex-induced vibration of slender cable experiencing shear flow[J]. Procedia Engineering, 2010(4):145-152.

[4] JAKOBSEN M L, SAYER M L. Hydrodynamic forces on piggyback pipelines[C]//Proceedings of the Fifth International Offshore and Polar Engineering Conference. 1995.

[5] CHUNG J S, CONTI R J. Flow-induced torsional moment and vortex suppression for a circular cylinder with cables[C]//Proceedings of the Fourth International Offshore and Polar Engineering Conference, ISOPE. 1994(3):447-459.

[6] KALAHATGI S G, SAYER P G. Hydrodynamic forces on piggyback pipeline configurations[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1997, 123(2):16-22.

[7] ZANG Zhipeng, GAO Fuping, CUI Jinsheng. Physical modeling and swirling strength analysis of vortex shedding from near-bed piggyback pipelines[J]. Applied Ocean Research, 2013,40:50-59.

[8] ZANG Zhipeng, GAO Fuping. Steady current induced vibration of near-bed piggyback pipelines: Configuration effects on VIV suppression[J]. Applied Ocean Reasearch, 2014,46:62-69.

[9] 成小飞, 王永学, 王国玉. 波流共同作用下海底子母管线水动力的物理模型试验研究[J]. 海洋学报, 2012,34(4):172-180. ( CHENG Xiaofei, WANG Yongxue, WANG Guoyu. Physical model experimental study of hydrodynamic forces on submarine piggyback pipeline under wave-current coexisting action[J].Acat Oceanlolgica Sinica,2012,34(4):172-180.(in Chinese))

[10] APOSTOLOS T P. Investigation of boundary layer suction on a wind turbine airfoil using CFD[D]. Technical University of Denmark,2010.

[11] MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model turbulence[R]. Heat and Mass Transfer 4, 2003.

[12] Recommended Practice DNV-RP-F109, On-bottom stability design of submarine pipelines[S]. 2010.

[13] TILDEN P M, DENNIS D B. The budgets of turbulent kinetic energy and reynolds stress within and above a deciduous forest[J].Agricultural and Forest Meteorlogy, 1991,53:207-222.

Research on vortex induced vibration of cable in piggy-back configuration

PAN Pan, CAI Bingyu, TAN Ailing, GUO Chaoyang, XIE Shuhong

(Zhongtian Technology Submarine Cables Co., Ltd., Nantong 226010, China)

The vortex-induced vibration characteristic of the piggy-back configuration adopted in the oil production was studied with the FSI method, and the results were compared with the single cable vibration under free span condition. The numerical simulation revealed that the amplitude of the lift force caused by the vortex street of the secondary cable varied over time due to the main pipe’s influence, but the lift force of the single cable was constant. The drag force of the cable in piggy-back was about 65% higher than the single cable with larger amplitude, and the turbulent kinetic energy in the wake along the cable showed random feature, thereby impacted the hydrodynamic force. By comparing the lift force and amplitude of the vibration perpendicular to the flow direction of the middle section of the cable, it revealed that the lift force due to vortex was the main reason for vertical vibration. The flow drag force combined with the vortex induced lift caused significant displacement and strain of the cable, and much effort must be taken to adjust the interval of the clamps and residual tension to relieve the fatigue damage of the cable in the piggy-back configuration.

piggy-back; vortex-induced vibration; free span; fluid-structure interaction; turbulence kinetic energy

P754

A

10.16483/j.issn.1005-9865.2015.06.006

1005-9865(2015)06-045-07

2014-08-19

国家高技术研究发展计划(863计划)(2012AA09A401)

潘 盼(1986-)，男，江苏句容人，博士，从事海洋柔性立管和脐带缆的研发。 E-mail:panp@chinaztt.com