不完备信息系统下基于分辨度的属性约简算法

李长清，张燕兰

（1.闽南师范大学数学与统计学院，福建漳州363000；2.闽南师范大学计算机学院，福建漳州363000）

不完备信息系统下基于分辨度的属性约简算法

李长清1，张燕兰2

（1.闽南师范大学数学与统计学院，福建漳州363000；2.闽南师范大学计算机学院，福建漳州363000）

针对不完备信息系统问题，引入容差关系下分辨度的概念，并由此提出一种基于分辨度的不完备信息系统属性约简算法，该算法更符合实际应用的需要.文章通过实例比较，证明该方法可行、有效.

不完备信息系统；容差关系；分辨度；属性约简

波兰学者Pawlak Z.于1982年提出的经典粗糙集理论［1］是一种处理不精确、不确定和模糊知识信息的数学工具，已经被成功应用于模式识别、人工智能、决策与分析、机器学习、智能信息处理［2-7］等领域.这种经典的粗糙集理论研究是限制严格的等价关系下的完备信息系统.而在应用中，由于数据测量和获取的限制，大量的数据存在缺失现象，信息系统普遍都不完备，因而，为处理这种不完备现象进行的研究引起广泛的关注.

1997年，Krysckiewcz M.［8］利用容差关系代替经典粗糙集中的等价关系，提出了一种不完备信息系统下基于容差关系的粗糙集拓展模型.随后，很多学者对不完备信息系统的处理进行了深入研究.例如，Meng等人［10］通过所研究对象关于属性得到的各种划分，给出了一种快速的属性约简算法；Wu［11］结合证据理论得到了不完备决策信息系统的属性约简方法；于海燕等人［12］在不完备决策信息中将决策表进行分解，然后按决策表提供的确定信息进行分层提取而得到确定规则；黄兵等人［13］研究了相容矩阵和分配决策矩阵，通过矩阵间的相互关系得到了不完备信息系统的一种有效处理方法；李长清［14］等人针对容差关系存在的局限性，给出一种基于重要度相似关系的粗糙集模型；汪凌［15］引入相容关系下条件属性矩阵和决策属性矩阵的相关概念，并由此提出一种基于矩阵的不完备信息决策系统规则获取算法；胡峰等人［16］提出了一种基于决策熵的不完备信息处理方法.

为了推进不完备决策信息系统的进一步研究，参照Krysckiewcz M.在文献［8-9］中提出的不完备信息系统的属性约简，本文从不完备信息系统中基于容差关系的分类特点，给出分辨度的概念，借助这个概念给出了一种有效的属性约简算法.

1　不完备信息系统

定义1［4］设S=〈U，A∪｛d｝〉为一个信息系统，其中U是论域，A∪｛d｝是非空有限属性集，A为条件属性集合，｛d｝为决策属性集合，且A∪｛d｝≠∅.∀a∈A∪｛d｝，有a∶U→Va，其中Va为a的值域.若存在u∈U，a∈A，使a（u）=*，则称S是不完备信息系统；否则称S是完备信息系统.

定义2［4］设S为不完备信息系统，∅≠B⊆A，B上的容差关系定义为：

2　基于分辨度的约简算法

定义6设U为论域，A=｛A1，A2，…，Am｝和B=｛B1，B2，…，Bn｝为U上的两个分类，若对∀Ai∈A，∃Bj∈B，使Ai⊆Bj，则称A细于B.

根据定义5和定义6，容易得到下面的这个定理.

定理1设S为不完备信息系统，∅≠B⊆A，a∈A，若U/TB细于U/T｛a｝，则LB细于U/T｛a｝，从而KB（a）=0.

定理2设S为不完备信息系统∅≠B⊆A， b∈B，若满足KB-｛b｝（b）＞0，则b为属性集B的核.

证明由于KB-｛b｝（b）＞0，故U中至少存在两点x1和x2在B-｛b｝中不可分辨，而对属性b可分辨.于是属性集B-｛b｝和B对论域U的分类情况不相同，因此b是核.

根据定理1，若某个属性对属性集分类情况不产生变化，则可知分辨度是0，于是该属性冗余，从而可删除.现在通过定理1与定理2，便得到一种约简算法.

在不完备信息系统S中，从核开始，逐步增加核以外相对分辨度最大的属性，验证所得属性集与原属性集的分辨度相等情况，一直到分辨度相等时，算法终止，从而得属性约简集.

算法具体过程如下：

输入：一个不完备信息系统S=〈U，A∪｛d｝〉，其中U为论域，A为条件属性集，d为决策属性.

输出：A的约简集Red.

步骤1：求出A的分辨度KA；步骤2：求出核属性集

令Red=core.验证是否满足KRed=KA，若满足，则转步骤5，否则转步骤3；

步骤3：若a∈A-Red满足

则令Red=Red∪｛a｝；

步骤4：验证是否满足KRed=KA，若满足，则转步骤5，否则转步骤3；

步骤5：输出Red，算法结束，所得到的Red就是系统的约简集.

我们以一个实例来分析此算法.

在一个不完备信息系统S=〈U，A∪｛d｝〉中，U=｛u1，u2，…，u6｝为论域，A=｛a1，a2，a3，a4｝为条件属性集，d为决策属性，见表1.

步骤1：计算A的分辨度KA：

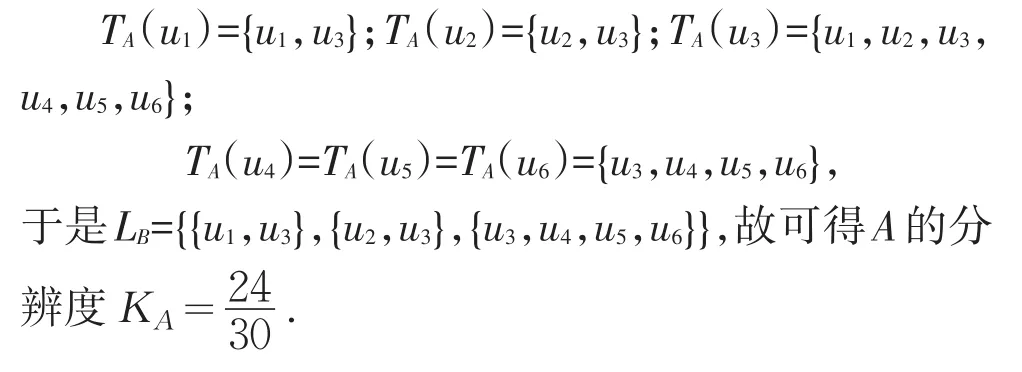
步骤2：求核core：

容易求得各属性的相对分辨度为：

3　实例分析

表1　不完备信息系统Tab.1Incomplete information system

步骤5：输出Red=｛a2，a3｝，于是｛a2，a3｝就是约简集.

在经典的不完备信息系统S=〈U，A∪｛d｝〉中，一个集合B⊆A称为此不完备信息系统的一个约简，若TB=TA，且∀C⊂B，TC≠TA.

对于上例给定的不完备信息系统，由经典的不完备信息系统的约简定义可以通过逐步验证得到约简集为｛a2，a3｝.

以上两种约简方法得到的约简集是一样的.由比较可以看出，用经典的约简方法只考虑了约简集与原条件属性集分类能力的一致性；而用相对分辨度进行约简时，不但简化了容差类，而且兼顾了各条件属性间的依赖关系，更符合实际应用的需要.

4　小结

属性约简一直以来都是粗糙集理论的热点课题.在前人已有成果的基础上，本文在不完备信息系统容差关系下进行研究，通过简化容差类进行属性约简，同时兼顾了各条件属性集间的依赖关系，比经典的约简方法更符合实际应用的需要.有关结论对不完备信息系统的研究具有一定的参考价值.

［1］Pawlak Z.Rough sets［J］.International Journal of Comput⁃er and Information Science，1982，11：341-356.

［2］Pawlak Z，Busse J G，slowinski R，et al.Rough sets［J］. communications of the ACM，1995，38（11）：89-95.

［3］王国胤.Rough理论与知识获取［M］.西安：西安交通大学出版社，2001.

［4］张文修，仇国芳.基于粗糙集的不确定决策［M］.北京：科学出版社，2005.

［5］王超，罗可.不完备信息系统中基于限制容差关系的属性约简方法［J］.计算机应用，2011，31（12）：3236-3239.

［6］莫京兰，吕跃进，郭恒.广义不完备信息系统中一种拓展粗糙集模型［J］.计算机工程与应用，2012，48（19）：126-130.

［7］陈家俊，苏守宝，金萍.一种对象完备度优先填补的决策树规则提取算法［J］.计算机应用与软件，2014，31（5）：264-267.

［8］Kryszkiewicz M.Rough set approach to imcomplete infor⁃mation systems［J］.Information Sciences，1998，112：39-49.

［9］Kryszkiewicz M.Rules in imcomplete information systems［J］.Information Sciences，1999，113：271-292.

［10］Meng Z Q，Shi Z Z.A fast to attribute reduction in incom⁃plete decision systems with tolerance relation-based rough sets［J］.Information Sciences，2009，179：2774-2793.

［11］Wu W Z.Attribute reduction based on evidence theory in incomplete decision systems［J］.Information Sciences，2008：1355-1371.

［12］于海燕，王道平，张霞.基于粒计算的不完备信息系统的规则提取方法［J］.计算机工程与应用，2009，45（8）：143-145.

［13］黄兵，周献中.不完备信息系统分配约简与规则提取的矩阵算法［J］.计算机工程，2005，31（17）：20-22.

［14］李长清，李克典.不完备信息系统下基于重要度相似关系的粗集模型［J］.海南师范大学学报：自然科学版，2008，21（4）：401-403.

［15］汪凌.不完备决策系统规则获取的相容矩阵算法［J］.计算机工程与应用，2015，51（1）：130-142.

［16］胡峰，陈曦，王小燕.基于决策熵的不完备信息系统的知识约简方法［J］.计算机工程与设计，2013，34（1）：289-292.

责任编辑：刘红

An Attribute Reduction Algorithm Based on Discernibility in Incomplete Information Systems

LI Changqing1，ZHANG Yanlan2
（1.School of Mathematics and Statistics，Minnan Normal University，Zhangzhou 363000，China；2.College of Computer，Minnan Normal University，Zhangzhou 363000，China）

For incomplete information systems，the concept of discernibility under tolerance relation was introduced.More⁃over，an attribute reduction algorithm in incomplete information systems based on discernibility was presented.Dependency relation between attributes can be known from the reduction gained by the algorithm.It is more suited to the needs of practi⁃cal application.An example was used to illustrate that the algorithm was feasible and more effective through comparison.

incomplete information systems；tolerance relation；discernibility；attribute reduction

TP 18

A

1674-4942（2015）04-0359-03

2015-09-17

国家自然科学基金项目（11471153，11526109）；福建省自然科学基金项目（2015J05011，2013J01029）；福建省中青年教师教育科研基金项目（JA14200，JA13198）；福建省省属高校专项计划资助项目（JK2014028）