一类p-Laplace型方程非平凡解的存在性

曲军恒，张进虎，陈风仪

（1.佛山科学技术学院信息科学与数学系，广东佛山528000；2.华南理工大学数学学院，广东广州510460）

一类p-Laplace型方程非平凡解的存在性

曲军恒1，张进虎2，陈风仪2

（1.佛山科学技术学院信息科学与数学系，广东佛山528000；2.华南理工大学数学学院，广东广州510460）

通过变量代换，将非线性p-Laplace问题转变为半非线性问题，然后利用山路引理及Cerami序列证明了此问题非平凡解的存在.

p-Laplace型方程；山路引理；Cerami序列；非平凡解

1　引言

现实科研与工程中，偏微分方程非常重要，特别是在物理领域与工程领域.它们中有很多问题都集中在如何解微分方程，线性微分方程因其特殊的形式，现阶段研究思路比较清晰，解决的比较彻底，但是非线性偏微分方程比较麻烦，研究下面一类非线性p-Laplace型方程解的存在性

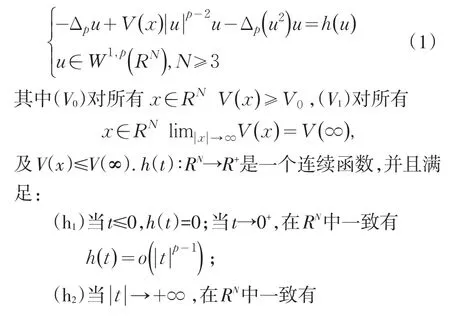
2　定理的证明

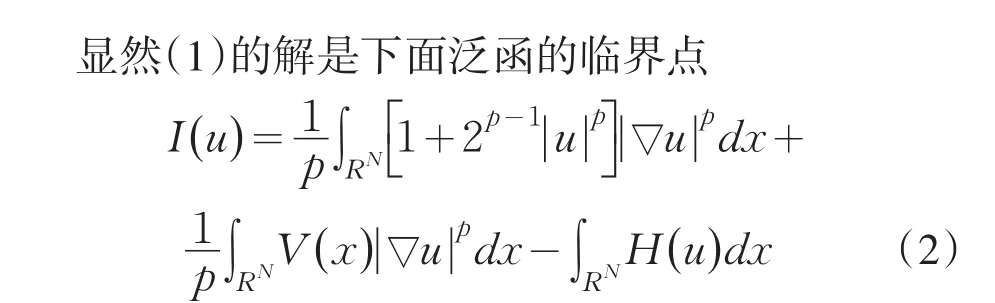
由于泛函I（u）在一般的Sobolev空间W1，p（RN）没有定义，进行如下的变量变换

证明见文献［1］.

接下来，我们建立山路引理的几何条件［2］.

引理2存在ρ0，a0＞0使得对所有的‖‖v=ρ0有

所以，当‖v‖=ρ0时，选择很小的ρ0，结论成立.引理3存在v∈W1，p（RN）使得J（v）＜0.

事实上，因为G-1（v）≤v由（h3），（h4）和引理1当t→+∞时，有

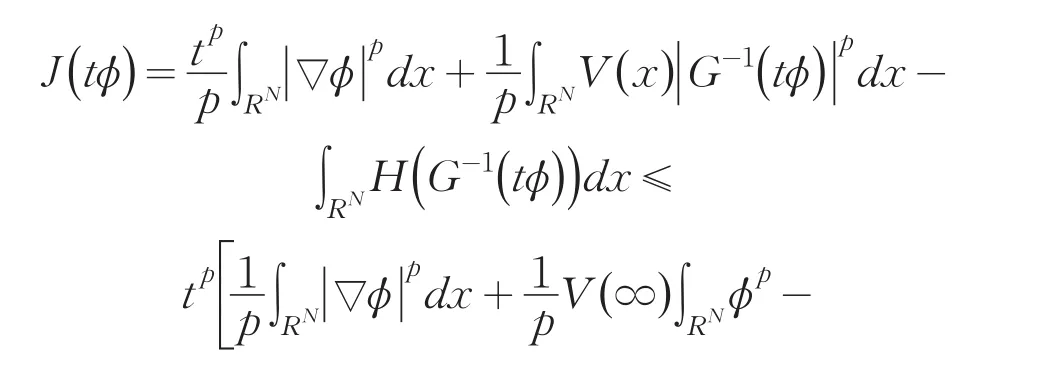
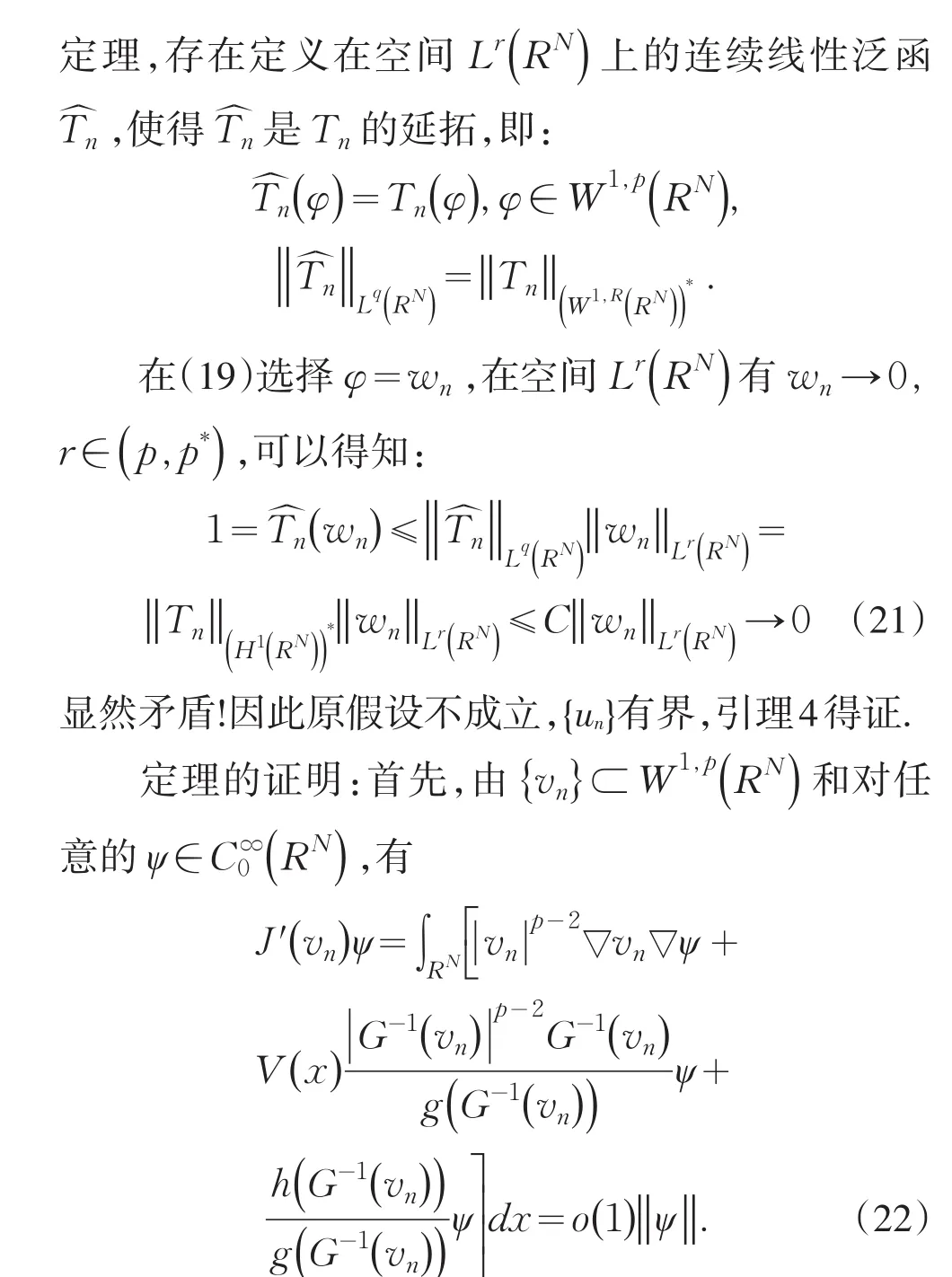
因为｛vn｝是一个Cerami序列，根据引理4知｛vn｝有界.所以存在v∈W1，p（RN）使得在W1，p（RN）中，有vn→v.由Lebesgue控制理论，可得

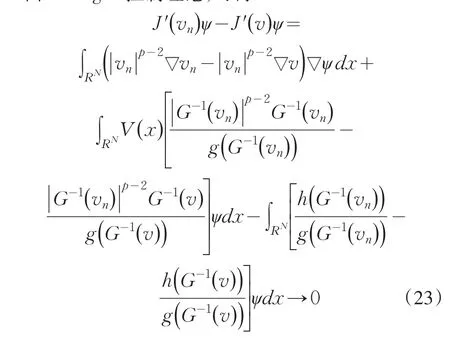
所以，v是（1）的一个弱解.

下面证明v≢0，反证法：假设v=0，我们声明｛vn｝也是定义的泛函～J∶W1，p→R的一个Cerami序列，其中

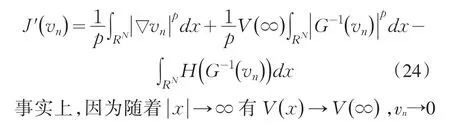
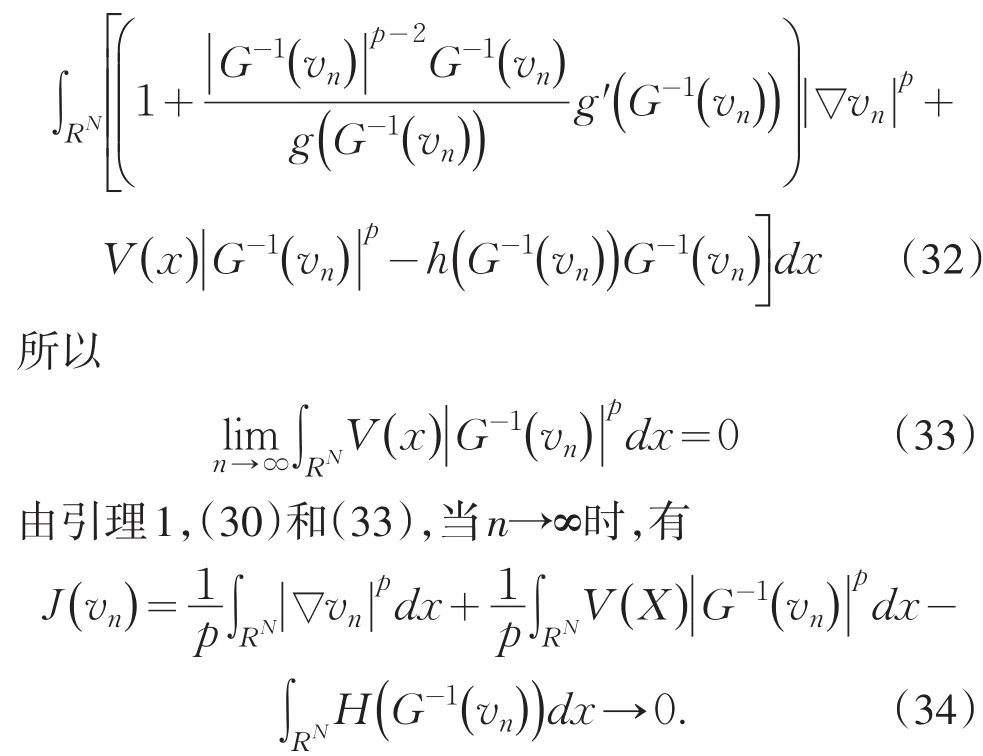
这样得到了一个矛盾的结果J（vn）→c＞0.所以，｛vn｝不会消失且存在k，R＞0，和｛yn｝⊂使得

这矛盾.所有v是一个非平凡解.

［1］Shen Y，Wang Y.Soliton solutions for generalized quasilin⁃ear Schrödinger equations［J］.Nonlinear Anal，2013，80：194-201.

［2］Yang J，Wang Y J，Abdelgadir A A.Soliton solutions for quasilinear Schrödinger equations［J］.J Math phy，2013，54（7）：1502-1507.

［3］Cheng Y K，Yang J.Positive solution to a class of relativistic nonlinear Schrödinger equation［J］.J Math Anal Appl，2014，411（2）：665-674.

［4］Silva EAB，Vieira G F.Quasilinear asymptotically periodic Schrödinger equations with subcritical growth［J］.Nonlinear Anal，2010，72：2935-2949.

责任编辑：刘红

The Existence of Nontrivial Solution to a Class of p-Laplace Type Equation

QU Junheng1，ZHANG Jinhu2，CHEN Fengyi2
（1.Information Science and Mathematics Department，Foshan University，Foshan 528000，China；2.School of Mathematics，South China University of Technology，Guangzhou 510640，China）

Using variable substitution，we converted a nonlinear p-Laplace type equation into a nonlinear elliptic equation. By Mountain Pass Lemma and Cerami sequence we showed the existence of nontrivial solution for a class of p-Laplace type equation.

p-Laplace type equations；Mountain pass theorem；Cerami sequence；Nontrivial solution

O 175.25

A

1674-4942（2015）04-0362-05

2015-10-17

国家自然科学基金项目（11461014）