求解随机二阶锥线性互补问题的一种光滑化SAA方法

王欢，张杰，洪志曼

（辽宁师范大学数学学院，辽宁大连116029）

求解随机二阶锥线性互补问题的一种光滑化SAA方法

王欢，张杰*，洪志曼

（辽宁师范大学数学学院，辽宁大连116029）

研究了随机二阶锥线性互补问题的收敛性问题并基于收敛性分析进行了数值实验.文章利用Chen-Harker-Kanzow-Smale（CHKS）光滑函数和SAA方法，提出了求解随机二阶锥线性互补问题的光滑化SAA方法.基于P性质，建立了收敛性分析，然后通过数值实验验证了算法的有效性.

随机二阶锥线性互补问题；CHKS光滑函数；Cartesian P性质

考虑如下随机线性锥互补问题：寻找到一个向量x∈K，使得：

其中F（x）=E［M（ξ（ω））］x+E［q（ξ（ω））］，M（·）∶Rm→Rn×n，q（·）∶Rm→Rn是随机映射，ξ∶Ω→Ξ⊂Rm是定义在概率空间（Ω，F，P）上的随机变量，E表示数学期望，K是Rn中的闭凸锥，表示为

是二阶锥（SOC），也称为冰激凌锥，定义为

其中‖·‖表示欧几里得范数.如果ni=1，则Kni是非负实数集R+.在本文中，假设M（ξ（ω）），q（ξ（ω））满足

由于问题（1）含有随机变量，称问题（1）随机二阶锥线性互补问题（SSOCLCP）这个模型属于随机均衡模型，在经济、力学、控制领域等中有重要的应用，尤其是当ni=1，i=1，2，…，m时，这个问题退化为如下的随机线性互补问题（SLCP）：寻找x∈Rn使得Gürkan、Özge和Robinson［1］在随机变分不等式的框架下提出了样本路径优化（SPO）方法求解SLCP，并通过数值试验验证了此方法的收敛性.Xu［2］提出了样本均值近似（SAA）方法求解SLCP问题，研究了样本平均近似问题的解的存在性和收敛性，并应用到求解带有随机约束的随机规划问题中.Zhang等［3］提出了一类光滑化SAA方法求解SLCP问题.如果期望值可以准确得到，则可用求解确定性二阶锥互补问题的方法如内点法［4-5］，光滑化牛顿法［6］等进行求解.但在实际问题中准确得到期望值的代价很大，很多学者建议采用SAA方法来求解，如Xu［2］，Wang［7］等.SAA方法的主要思想是产生一组独立同分布样本ξ1，…，ξn构造样本均值近似期望值.本文提出一种求解SSOCLCP的方法，这种方法的基本思想是首先利用SAA方法和光滑化函数，把SSOCLCP转化为光滑的无约束优化问题，然后通过求解一系列的光滑优化问题来得到SSOCLCP的解.利用若当代数和Car⁃tesian P性质对这种方法的收敛性进行了分析，并分别利用matlab工具箱和非精确牛顿法进行了数值实验，验证了方法的有效性.

为了建立方法的收敛性分析，首先介绍一下欧几里得若当代数［8］.欧几里得若当代数（H0，∘，〈·，·〉）是定义在实数域上的有限维内积空间，（x，s）→x∘ s∶H0×H0→H0是双线性映射，并满足下列几个条件：

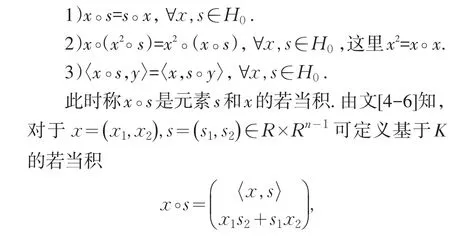
其中〈·，·〉表示欧几里得内积.此时记x2≔x∘x，x+s为通常的向量加法，则可知对所有的x∈Rn，x2∈K，而且如果x∈K，则存在K中的唯一向量使得

1　光滑化SAA问题构造

定义WL是问题（2）的解.是问题（3）的解且W0是SSOCLCP的解.为了确保解的近似程度比较好，这里考虑样本容量充分大时的情形.

2　收敛性分析

3　数值实验

结合上面的收敛性分析给出两个例子，并分别用Matlab中的fminsearch函数和非精确牛顿法对光滑化的SAA问题进行求解，下面给出非精确牛顿法求解

如果上述系统不兼容或者下面情况

ξ=（ξ（1ω），ξ（2ω），ξ（3ω）），ξ（1ω），ξ（2ω），ξ（3ω）是独立随机变量，并且ξ（1ω）是服从EXP（λ=2.5）的指数分布，ξ（2ω）是服从［0，1］的均匀分布，ξ（3ω）是服从N（μ，σ2）的正态分布，μ=0.5，σ=0.1.对于上述问题在Mat⁃lab中采用fminsearch函数进行求并取光滑化参数t= 0.01，并用N，，Obj，liter分别表示光滑SAA问题的样本量，最优解集，最优值及迭代次数.计算结果见表1.

表1　例1的计算结果Tab.1Calculation results of case 1

通过简单计算可知这个问题有唯一解s*=（1.0000，1.0000）T.表1的实验结果表明本文的方法可以得到问题的一个很好的近似解.

例2考虑随机二阶锥线性互补问题（1），其中

q（ξ（ω））=（-4ξ3（ω），-1，0，-5ξ1（ω）），ξ=（ξ1（ω），ξ2（ω），ξ3（ω）），ξ1（ω），ξ2（ω），ξ3（ω）是独立随机变量，ξ1（ω）是服从EXP（λ=2.5）的指数分布，ξ2（ω）是服从［0，1］的均匀分布且ξ3（ω）是服从N（μ，σ2）的正态分布，μ=0.5，σ=0.1.对于上述问题，分别用Matlab中的fminsearch函数和非精确牛顿法LSINA来进行求解，实验中取t=0.01，计算结果见表2.

通过简单计算可知这个问题有唯一解s*=（2.0000，1.0000，0.0000，1.0000）T.表2的实验结果表明本方法可以得到问题的一个很好的近似解.通过表2，发现在采用fminsearch函数所得的解更精确，但非精确牛顿方法迭代次数相对较少.

表2　例2的计算结果Tab.2Calculation results of case 2

4　结论

本文提出了一个求解随机二阶锥线性互补问题的光滑化样本均值近似方法，建立了算法的收敛性理论并通过数值实验验证了方法的有效性.

［1］Gurkan G，Ozge A，Robinson S.Sample-path solution of stochastic variational Inequalities［J］.Mathematical Program⁃ming，1999，84：313-333.

［2］Xu H.Sample average approximation methods for a class of stochastic variational inequality problems［J］.Asia-Pacific Journal of Operational Research，2010，27：103-119.

［3］Zhang J.A class of smoothing SAA methods for a stochastic linear complementarity problem［J］.Numerical algebra，Control and optimization，2012，2：145-156.

［4］Monteiro R，Tsuchiya T.Polynomial convergence of pri⁃mal-dual algorithms for the second-order cone programs based on the MZ-family of directions［J］.Mathematical Programming，2000，88：61-83.

［5］Chen J，Tseng P.An unconstrained smooth minimization re⁃formulation of the second-order cone complementarity problem［J］.Mathematical Programming，2005，104：293-327.

［6］Pan S，Chen J.A regularization method for the second-or⁃der cone complement-arity problem with the Cartesian P0-property［J］.Nonlinear Analysis，2009，70：1475-1491.

［7］Wang M，Lin G，Gao Y，et al.Sample average approxima⁃tion method for a class of stochastic variational inequality problems［J］.Systems Science and Complexity，2001，24：1143-1153.

［8］Faraut J，Korabyi A.Analysis on symmetric cones［M］.Ox⁃ford：Clarendon Press，1994.

［9］Chen C，Mangasarian O.A class of smoothing functions for nonlinear and mixedcomplementarity problems［J］.Compu⁃tational Optimization and Applications，1996，5：97-138.

［10］Fukushima M，Luo Z，Tseng P.Smoothing functions for second-order-cone complementarity problems［J］.SIAM J Optim，2002，12（2）：436-460.

［11］Facchinei F，Fischer A，Kanzow C.Inexact Newton meth⁃ods for semismooth equations with applications to variation⁃al inequality problems［J］.Di Pillo G，Giannessi F.Nonlin⁃ear Optimization and Applications.New York：Plenum Press，1996：125-139.

责任编辑：刘红

A Smoothing SAA Method for a Stochastic Second-order Cone Linear Complementarity Problem

WANG Huan，ZHANG Jie*，HONG Zhiman
（School of Mathematics，Liaoning Normal University，Dalian 116029，China）

In this paper，we studied the convergence of the random second-order cone linear complementary problems and experiments were carried out based on convergence analysis.Based on the Chen-Harker-Kanzow-Smale（CHKS）smooth⁃ing function and sample average approximation（SAA）method，a smoothing SAA method was proposed for solving a stochas⁃tic second-order cone linear complementarity problem.Convergence analysis was established by the P property.At last，the efficiency of the method was verified by some numerical tests.

stochastic second-order cone linear complementarity problem；CHKS smoothing function；Cartesian P property

O 221

A

1674-4942（2015）04-0355-04

2015-09-17

国家自然科学基金项目（11201210）；辽宁省高等学校杰出青年学者成长计划（LJQ2015059）