基于多目标有效全局优化算法的直线感应电动机优化设计
宫金林 王秀和
(山东大学电气工程学院 济南 250061)
基于多目标有效全局优化算法的直线感应电动机优化设计
宫金林王秀和
(山东大学电气工程学院济南250061)
直接针对有限元模型的电机优化设计周期长、效率低。多目标有效全局优化算法基于Kriging代理模型引导采样,从而可以减少优化过程中有限元模型的迭代次数,缩短优化设计周期,并且保证了优化结果的准确度。同时将并行计算的方法与多目标有效全局优化算法相结合,进一步提高了算法的效率。最后成功地将该算法应用于直线感应电动机的三维有限元模型的优化设计中,得到了经过有限元模型分析值组成的二维Pareto最优前沿解集,为基于有限元模型的直线感应电动机优化设计提供了新方法。
多目标有效全局优化Kriging代理模型三维有限元模型直线感应电动机
0 引言
由于直线电动机及其系统具有结构简单、加速度大、传动零部件间机械损耗少、噪声低等优点,使得直线电动机技术在最近几十年来得到了迅速的发展,其研究也更加的深入和广泛,应用效果也越来越好。因此越来越多的科研机构、高校加入到直线电动机技术研究的行列中,同时更多的公司开始开发、制造和采用直线电动机技术[1]。
随着计算机辅助设计技术的不断完善和发展,一些数值分析方法,为电机设计及控制提供了新的途径,大大缩短了产品的设计周期并降低了开发成本。有限元分析方法可以应用于任何微分方程所描述的各类物理场中,并且在电磁场问题的求解中取得了很好的效果,也是现今电机设计中应用最为广泛的方法之一[2]。相比于二维有限元方法,用三维有限元方法对直线电动机进行分析,不但可以考虑所用材料的非线性、纵向边端效应,还可以同时考虑横向边端效应,获得较高的计算准确度[3]。
电机优化设计是一个分析—修改—再分析的循环迭代过程,需要多次调用仿真模型对性能进行比较和评估。三维有限元模型计算准确度高,但是分析时间长,从而导致整个优化设计周期长。此外,有限元模型在网格的离散化和网格的自适应划分过程中会产生数字化噪声,这样会影响优化算法的收敛性。解决上述计算准确度和优化时间之间矛盾的一个可行方法是采用基于代理模型的优化方法,即根据有限元模型的分析结果构造一个计算量小,但计算结果与有限元数值分析结果相近的数学模型来“代理”相应的有限元模型,而原优化问题在代理模型上来实现。这样可以减少有限元模型的调用次数,从而减少优化时间[4,5]。然而直接基于代理模型的优化结果是代理模型的预测值,存在近似误差,所以这种方法十分依赖于最初所建立的代理模型的准确度,且优化算法容易陷于局部最优解。针对此问题,M. Schonlau等[6]提出以Kriging模型为代理模型的单目标有效全局优化算法(Efficient Global Optimization,EGO)算法,该算法在选取校正点时综合考虑了Kriging模型的预测值和预测准确度,以期望提高(Expected Improvement, EI)为加点准则,避免了优化过程局部收敛的风险。该方法是综合考虑预测值和预测误差估计值来增加样本点,提高代理模型的近似准确度并进行序列优化设计的优化方法[7,8]。为了解决工程设计中的多目标优化问题,Kreuawan Sangkla[9]将PI(Pseudo distance)准则引入到EGO算法当中,提出了基于Kriging模型引导采样的多目标有效全局优化算法MEGO,优化得到的Pareto解集均为高准确度模型的评估值。本文将并行计算的方法与MEGO算法相结合,进一步提高了MEGO算法的效率,并将算法成功地应用于直线感应电动机的三维有限元模型的优化,得到经过有限元模型分析值组成的Pareto最优解集。
1 三维有限元模型分析
1.1直线感应电动机基本结构
双边直线感应电动机的结构如图1所示。电机有两个完全一样的面对面放置的初级和一个次级组成。初级线圈采用同心式绕组,次级由一定厚度的铝制导轨组成。电机是为轨道交通用的牵引电机,初级作为动子安装在机车上,次级(铝制导轨)作为定子安装在钢轨中间。当在初级绕组中通入三相对称正弦电流后,在气隙中产生了一个行波磁场。次级导条在行波磁场切割下,将会产生感应电动势及感应电流,并和气隙磁场相互作用产生电磁推力。在这个电磁推力的作用下,初级就顺着行波磁场运动方向推动目标前进。

图1 直线感应电动机基本结构Fig.1 Basic structure of linear induction motor
1.2三维有限元模型分析
直线电动机与旋转电机本质的区别在于前者的铁心是长直的、两端开断的铁心,从而会引起各相绕组互感不相等以及存在脉振磁场、反向磁场的现象,这种现象称为直线感应电动机的静态纵向边端效应。直线电动机气隙内磁场的分布是不均匀的,并且随着电机速度的增加,这种不均匀性更加明显,这种现象被称为直线电动机的动态纵向边端效应[10,11]。此外,由于直线感应电动机初级和次级的宽度都是有限的,次级电流以及次级板对气隙磁场均会产生影响,这种影响称为直线电动机的横向边端效应。利用传统的解析方法很难对这两种边端效应进行分析,然而三维有限元方法可以同时考虑纵向和横向两种边端效应以及材料的非线性,从而得到准确度较高的模型。
利用商业有限元软件Vector Fields[12]建立了如图2所示的三维有限元模型。

图2 三维有限元模型及t=0时刻磁通分布情况Fig.2 3D finite element model flux distribution at t=0
图3所示为直线电动机在一定速度下气隙磁场的磁通密度幅值的分布情况。直线电动机的纵向边端效应会在次级进入端和滑出端产生涡流,且仅在初级覆盖的范围内存在。次级进入端的表面磁场从零增大到气隙合成值,滑出端是从气隙合成值衰减到零,而且两端磁场的不对称性会随着初级速度的增大而增大[13,14],从而验证了直线电动机的纵向边端效应。
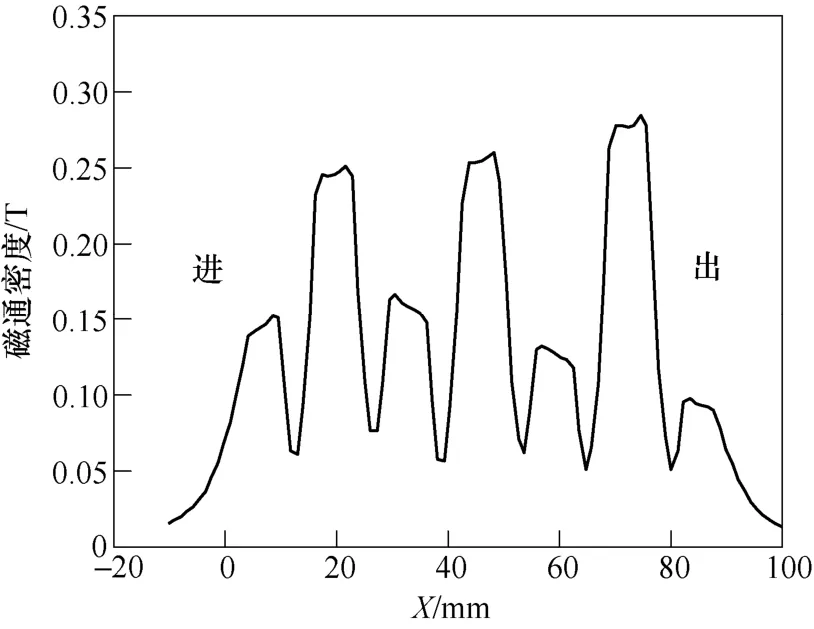
图3 气隙磁通密度振幅分布Fig.3 Amplitude of flux density in the air gap
2 多目标有效全局优化算法
有效全局优化算法是基于Kriging代理模型引导采样的算法。它可以同时利用Kriging模型的计算速度和有限元模型的分析准确度。
2.1Kriging模型基本理论
Kriging模型具有良好的高度非线性近似能力、在训练样本点处无偏估计,并且能够对未知样本点处的误差估计其值,非常适合作为代理模型[15]。
有效全局优化算法利用Kriging模型分别替代目标函数和约束函数。利用Kriging模型方法,一个未知函数y( x)可以表示为[16]

式中,B( x)为回归模型,一般为多项式模型,可以给出未知函数y( x)的全局近似;Z( x)为随机分布的误差,提供对未知函数局部偏差的近似,其具有如下统计特性
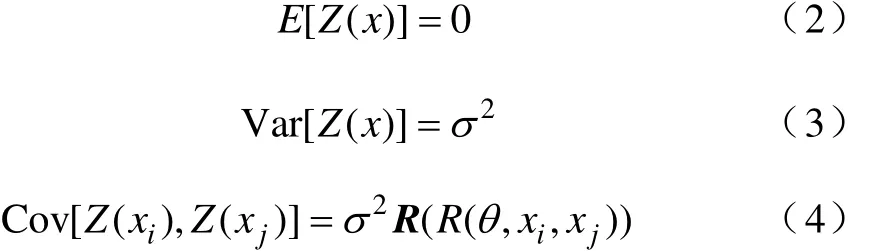
式中,R(θ,xi, xj)是以θ为参数关于xi、xj的相关函数;R(R(θ,xi, xj))为相关函数矩阵。Kriging模型中常用的核函数为高斯函数。

式中,nv为变量的数量;pk∈[0,2]可以控制未知函数y( x)的平滑度;θk通过极大似然估计法获得θk≥0且θk的大小决定着Kriging模型的平滑度及准确性的选择:当θk数值较小时(比如θ=10-3),Kriging模型具有较好的平滑度,当θk数值较大时(比如θk=20),Kriging模型在已知样本点处具有无偏估计,但是在未知点会有较大的误差。
Kriging代理模型的预测值表示为

相比于其他代理模型,Kriging模型最大的优势在于可以给出函数在未知点的预测值与实际值的误差估计值
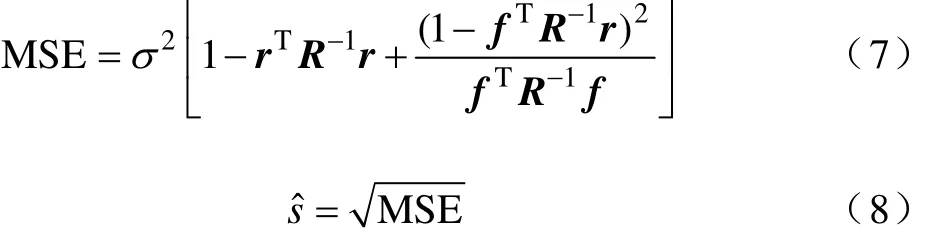
2.2有效全局优化算法
图4为采用并行计算的有效全局优化算法的流程图。此算法采用了多点加点准则和并行计算的方法,在保证优化结果准确度的前提下,显著地缩短了优化时间,提高了算法的有效性。
2.2.1初始样本点的选择
优化算法开始于初始样本点的选取。有效全局优化算法对初始Kriging代理模型准确度没有很高的要求。优化过程中,算法选取的样本点会逐渐逼近实际的Pareto最优解集,因此Kriging模型的准确度在最优解集周围不断提高。针对有限元模型的特点,采用空间填充的方法[4]——拉丁超方体方法选取30个初始样本点。根据有限元模型的评估值,对每个目标函数和约束函数建立初始Kriging模型。
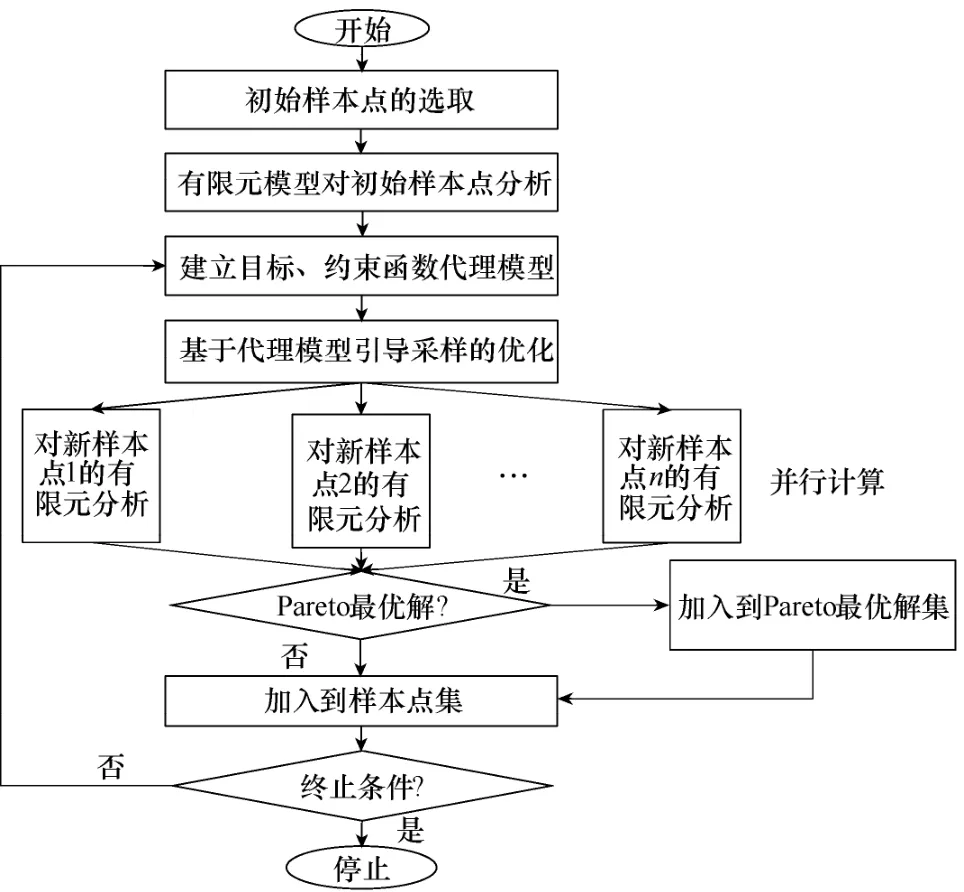
图4 采用并行计算的多目标有效全局优化流程Fig. 4 Flowchart of multi-objective efficient global optimization
2.2.2基于代理模型引导采样的加点准则
利用Kriging代理模型中提供的预测值的标准误差的估计值构建的多目标PI(Pseudo distance)加点准则。新的样本点的选取是通过对PI的最大值的求取来确定的。基于Pareto最优解集中非支配性的概念,PI由两部分组成:支配距离Dd(dominated distance)和相邻距离Dn(neighboring distance),其表达式为式(9)~式(11)。

式中,m为目标函数的个数;ndom为具有非支配性的点的个数;fi_min、fi_max分别代表当前迭代第i个目标函数的最大值和最小值;)为Kriging代理模型对第i个目标函数的预测值;i(x)为与相关的标准差;为距离Pareto最优解集所有点最近点的第i个目标函数值。
图5中给出了两个例子,用来解释如何利用PI准则选取新的样本点。图5a给出了具有最大非支配性距离Dd的样本点的选取。假设当前得到Pareto最优解集是由P1、P2、P3、P4和P5五个点组成的,那么迭代新产生的T1、T2两点中,将会选取T1点为新的样本点。因为T1点到其他五个点的非支配性距离大于T2点。图5b中,根据相邻距离Dn的定义,如何选取新的样本点。Dn的距离的目的是为了使得Pareto最优解集在解空间中具有良好的覆盖性,所以选取T3点为新样本点而不是T4点。

图5 PI准则Fig.5 PI criteria
2.2.3并行计算方法
利用并行计算的方法,可以充分利用多核计算机的计算能力,提高优化算法的效率,减少优化时间,其具体步骤如下。
(1)首先根据加点准则选取样本点。
(2)利用Kriging代理模型对新样本点的预测值来重新构造新的代理模型。
(3)以上两步循环,直到新选取的样本点数等于计算机核数。
利用Matlab中的并行计算工具箱,将上述方法中选取的多个样本点用有限元方法在多核计算机上同时分析,然后对分析结果进行判断,进行到流程图4的下一步,直到满足算法终止条件,优化过程结束。
3 基于三维有限元模型的直线电动机多目标优化
针对直线感应电动机的特点,提出了多目标优化问题,利用多目标有效全局优化算法对电动机的三维有限元模型进行优化。
3.1多目标优化问题
直线感应电动机的多目标优化问题的数学描述如式(12)所示。优化问题中含有两个目标函数和两个约束函数,目的是尽可能地减少电动机的质量和降低电动机的损耗。根据直线电动机中三相电流的不平衡性,设计了Eq≤10%的约束。
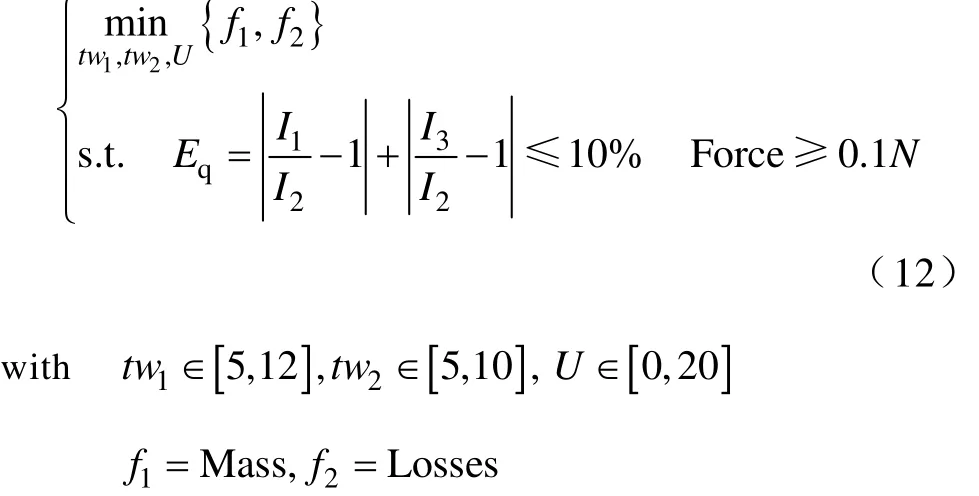
式中,Mass为电动机的重量;Losses为电动机的总损耗(铁耗+铜耗);Force为电机产生的推力;Eq为电机绕组三相电流平衡性;tw1为电机铁心两端齿的宽度;tw2为同心式绕组中心齿的宽度;U为施加的初级电压有效值。
优化问题中涉及到的电机的几何参数如图6所示。
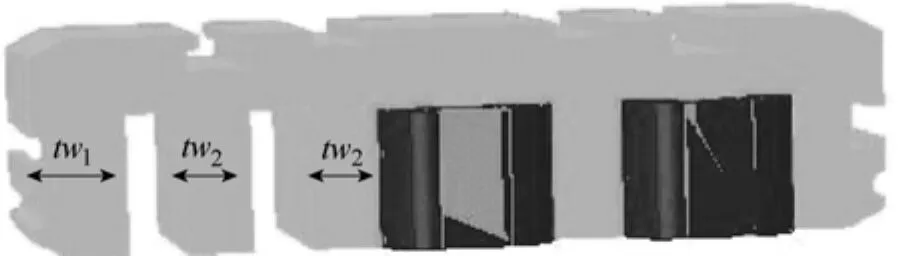
图6 优化问题中的几何参数Fig.6 Geometrical variables of the optimization problem
3.2优化结果
优化算法共设置选取100个样本点用于有限元模型分析。其中前30个样本点采用拉丁超方体方法选取,用于构建初始Kriging代理模型,后70个样本点采用多目标有效全局优化算法中介绍加点准则选取。整个优化过程共耗时大约一个星期的时间,得到了如图7中所示“●”组成Pareto最优前沿解集。此外,为了和传统的基于代理模型的优化算法相比较,还利用NSGA-II遗传算法直接对初始的Kriging代理模型进行优化,为初始种群个体随机选定100个,共交叉选取100代,此优化过程共耗时半个小时。优化结果为图7中“*”组成的Pareto最优前沿解集。图7中“◆”表示直线电动机的初始设计方案,与多目标有效全局优化算法得到的Pareto最优前沿解集相比较,无论是电动机的损耗,还是电动机的质量都有可以改善的空间。
用传统的基于代理模型的直接优化设计周期短,但是得到的Pareto最优解是代理模型的预测值,十分依赖初始代理模型的准确度。采用多目标有效全局优化算法优化设计周期相对较长,但是对初始Kriging代理模型准确度依赖性小,得到Pareto最优解均是三维有限元模型的分析值,准确度高,可以为进一步的样机设计提供更可靠的选择。
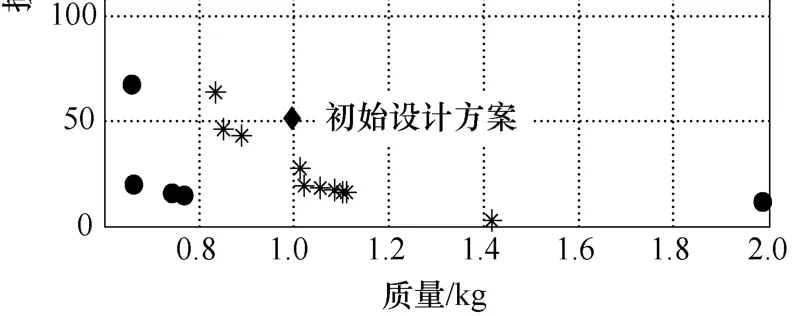
图7 Pareto最优前沿解集Fig.7 Pareto front solution
4 结论
本文首先利用三维有限元方法对双边直线感应电动机进行分析,验证了直线电动机的边端效应。其次将并行计算方法和多目标有效全局优化算法相结合,成功应用于直线感应电动机的三维有限元模型的优化,得到了经过有限元模型分析值组成的Pareto最优前沿解集。该方法不但降低了对代理模型准确度的依赖性,而且进一步减少了有限元模型分析环节的时间,缩短了优化周期。优化结果与初始设计方案相比,无论是电动机的重量,还是电动机的损耗都可以得到很大的改善。因此本文为针对电动机有限元模型的多目标优化设计提供了新方法。
[1] Ye Y, Lu Q. Research and development of linear motor technology in China during recent decade[C]. The 8th Symposium on Linear Drives for Industry Applications (LDIA2011), Eindhoven, Netherlands, 2011.
[2] Bianchi N. Electrical machine analysis using finite elements[M]. Taylor & Francis Group: CRC Press, 2005.
[3] SelÇuk A H, Kürüm H. Investigation of end effects in linear induction motors by using the finite element method[J]. IEEE Transactions on Magnetics, 2008, 44(7): 1791-1795.
[4] Wang G, Shan S. Review of meta-modeling techniques in support of engineering design optimization[J]. Journal of Mechanical Design, 2007, 129(4): 370-380.
[5] 王雅玲, 徐衍亮, 刘西全. 双定子永磁同步发电机(I)——结构原理及其响应面法设计[J]. 电工技术学报, 2011, 26(7): 167-172.
Wang Yaling, Xu Yanliang, Liu Xiquan. Dualpermanent magnet synchronous generator(I)—schematic structure and design based on response surface method[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 167-172.
[6] Schonlau M. Computer experiments and global optimization[D]. Waterloo: University of Waterloo, Ont., Canada, 1997.
[7] Jones D R. A taxonomy of global optimization methods based on response surfaces[J]. Journal of Global Optimization, 2001, 21(4): 345-383.
[8] 王红涛, 竺晓程, 杜朝晖. 基于Kriging代理模型的改进EGO算法研究[J]. 工程设计学报, 2009, 16(4): 266-270.
Wang Hongtao, Zhu Xiaocheng, Du Zhaohui. Research on improved EGO algorithm based on Kriging surrogate model[J]. Journal of Engineering Design, 2009, 16(4): 266-270.
[9] Kreuawan S. Modelling and optimal design in railway applications[D]. France: Ecole Centrale de Lille, 2008.
[10] Gieras J. Linear induction drives[M]. London: Oxford Science Publications, 1994.
[11] 叶云岳. 直线电机技术手册[M]. 北京: 机械工业出版社, 2005.
[12] Vector fields software: 2D AC, 3D Electra/SS manuals.
[13] 鲁军勇, 马伟明, 李朗如. 高速长初级直线感应电动机纵向边端效应研究[J]. 中国电机工程学报, 2008, 28(30): 73-78.
Lu Junyong, Ma Weiming, Li Langru. Research on longitudinal end effect of high speed long primary double-sided linear induction motor[J]. Proceedings of the CSEE, 2008, 28(30): 73-78.
[14] Gong J, Gillon F, Brochet P. Magnetic and thermal 3D finite element model of a linear induction motor[C]. IEEE Vehicle Power and Propulsion Conference (VPPC2010), Lille, France, 2010: 1-6.
[15] Simpson T W, Poplinsk J D, Koch P N, et al. Metamodels for computer-based engineering design: survey and recommendations[J]. Engineering and Computers, 2001, 17(2): 129-150.
[16] Kriging model toolbox, available online: http://www2. imm.dtu.dk/~hbn/dace/
Optimal Design of a Linear Induction Motor Using Multi-Objective Efficient Global Optimization
Gong JinlinWang Xiuhe
(Shandong UniversityJinan250061China)
Integration of finite element models (FEM) in the optimal design process of electrical machine is complex and time-costly. The multi-objective efficient global optimization (MEGO) algorithm uses Kriging surrogate model as a guide on the optimization problem. The computationally expensive FEM is replaced by Kriging surrogate model, which can reduce the iterations of the FEM in the optimal design process. A Parallel strategy is integrated with MEGO in order to further save the time of optimization. A multi-objective optimization is achieved, by applying the MEGO algorithm to a 3D FEM of the linear induction motor. A 2D Pareto set composed of 3D FEM solutions is obtained with an affordable time-cost. This paper provides a new method for the optimal design of linear induction motor with FEM.
Muti-objective efficient global optimization, Kriging Surrogate model, 3D finite element model, linear induction motor
TM351
宫金林男,1983年生,博士,讲师,研究方向为直线电机优化设计。
王秀和男,1967年生,教授,博士生导师,研究方向为电机优化设计。
国家自然科学基金青年项目(51307099)和山东大学自主创新基金项目(2013HW002)资助。
2013-11-21改稿日期 2014-05-30

