异步电机新型占空比直接转矩控制方案
李政学 张永昌 李正熙 班晓娟 杨海涛
(1. 北京科技大学计算机与通信工程学院 北京 100083
2. 北方工业大学 北京市电力电子与电气传动工程研究中心 北京 100144)
异步电机新型占空比直接转矩控制方案
李政学1张永昌2李正熙2班晓娟1杨海涛2
(1. 北京科技大学计算机与通信工程学院北京100083
2. 北方工业大学 北京市电力电子与电气传动工程研究中心北京100144)
传统的基于矢量表的异步电机直接转矩控制(ST-DTC)存在较大的稳态误差以及转矩脉动等问题。目前已经提出了一些通过优化有效电压矢量占空比来减小转矩脉动的方法,然而,这些方法不仅计算复杂而且严重依赖电机参数。通过深入分析每个电压矢量引起的转矩和定子磁链变化率的基础上,提出一种简单且非常有效的占空比控制方法。该方法在占空比的计算中考虑了电机转速的影响,能同时减小输出转矩脉动及其稳态误差,并且尽可能保持了传统DTC结构简单和鲁棒性强的优点。仿真和实验结果验证了所提方法的有效性。
直接转矩控制异步电机脉动减小占空比稳态误差
0 引言
Depenbrock和Takahashi在20世纪80年代中期各自提出了直接转矩控制理论[1,2]。发展至今,矢量控制(Field Oriented Control,FOC)和直接转矩控制已经成为高性能交流调速领域中最为常用的两种方法[3]。相比于矢量控制,传统基于矢量表的直接转矩控制(Switching-based Direct Torque Controlled,ST-DTC)在静止的定子坐标系中进行计算,无需旋转坐标变换、电流调节器和脉宽调制模块[1-4];它使用两个滞环比较器和一个矢量表,根据磁链和转矩的瞬时误差选择使定子磁链和转矩向各自的给定值变化的电压矢量,因此具有非常简单的结构和快速的动态转矩响应能力。另外,DTC在运算中使用的电机参数非常少,大大减小了电机参数波动对控制性能的影响[5]。然而,在数字控制中,由于使用固定的采样频率以及存在数据处理引起的时间延迟,因此数字控制方式下的磁链和转矩脉动会超出所设定的容差范围,产生不期望的转矩和磁链脉动及较大的转矩稳态误差[6,7]。
为了解决上述问题,国内外众多学者已经提出了许多方法,空间矢量调制直接转矩控制(Space Vector Modulation-Direct Torque Controlled,SVMDTC)技术就可以很好地解决这个问题[8-11]。SVM-DTC技术的基本思想是,在每一个控制周期中,通过计算得到一个能够恰好补偿当前定子磁链和转矩误差的电压矢量。该电压矢量可以用两个相邻的有效电压矢量和零电压矢量合成得到。这种基于SVM技术的DTC算法可以极大地减小输出转矩的脉动,同时获得了恒定的开关频率。但是,它的计算量非常大,而且使用了更多的电机参数。虽然控制性能有所提高,却丧失了DTC控制结构简单的优点。
模型预测直接转矩控制(Model Prediction-Direct Torque Controlled,MP-DTC)技术也获得了广泛研究和关注[12-16]。这种方法与ST-DTC的相似之处是都直接选择最终电压矢量,但MP-DTC选择矢量时是依赖于系统模型和评价函数,而非ST-DTC中的矢量表。例如文献[12]通过对每个可能开关状态代价函数的评估,选择最能满足性能要求的电压矢量输出。文献[13]提出一个三电平逆变器馈电的DTC方案,它使用多步预测取得开关频率减小,同时控制转矩、磁链和中点电位在各自的滞环带内的效果。MP-DTC相比ST-DTC有更好的稳态性能,但是计算量很大,对模型和参数的准确度要求较高。
另一种减小转矩脉动的方法是采用占空比控制技术,该方法与SVM-DTC技术相比复杂性有所降低。它的基本思想是,在每个采样周期中,有效电压矢量只作用该周期的一部分时间,而剩余时间选择零电压矢量。根据获得有效电压矢量占空比的优化方法不同,可以分为[17-20]:无差拍控制、平均转矩控制和转矩脉动最小控制等。另外,还可以采用模糊逻辑自适应方法[21,22]来获得占空比。以上这些方法[17-22]都取得了很好的控制性能,但是计算量较大,并且严重依赖电机参数。因此文献[18]针对永磁同步电机提出一个简单占空比确定方法,能同时减小转矩和定子磁链的脉动,获得了优良的性能,然而该方法在占空比的确定中没有考虑电机转速的影响,导致转矩的稳态误差比较大,同时也没有获取关键控制参数的简单解析方法。
本文在深入研究每个电压矢量引起的转矩和定子磁链变化率的基础上,针对异步电机提出一种简单且非常有效的占空比确定方法。该方法保持了传统DTC的结构简单性,在占空比计算中考虑了电机转速的影响,能同时减小输出转矩脉动和其稳态误差。为了进一步改善系统性能,使用基于全阶观测器的方法观测定子磁链,可以在全速域范围内准确地观测磁链[23]。仿真和实验结果证明了本文所提方法的可行性和在减小转矩脉动方面的有效性。
1 异步电机DTC稳态性能分析
1.1直接转矩控制原理
标准的两电平电压源逆变器(VSI)的输出只有8种电压矢量,包括6个有效电压矢量(V1~V6)和2个零电压矢量(V0,V7)。根据有效电压矢量的空间位置,坐标平面分为6个扇区,如图1所示。

图1 传统基于矢量表的DTC工作原理Fig.1 Conventional ST-DTC operating principle
假定定子磁链矢量落在第1扇区,电机转速为逆时针方向。应用电压矢量V2、V3可以增大转矩,而V5、V6可以迅速减小转矩。同理,V2、V6可以增大磁链幅值,而V3、V5则减小磁链幅值。当V0或V7作用时,定子磁链幅值保持不变,转矩将减小。
1.2定子磁链和转矩变化率的深入分析
对于电压源逆变器馈电的DTC系统,电压矢量是唯一可控制的输入变量,因此希望解析推导出转矩和定子磁链变化率与电压矢量之间的关系。
在αβ静止坐标系中,利用空间矢量表示的电机方程为
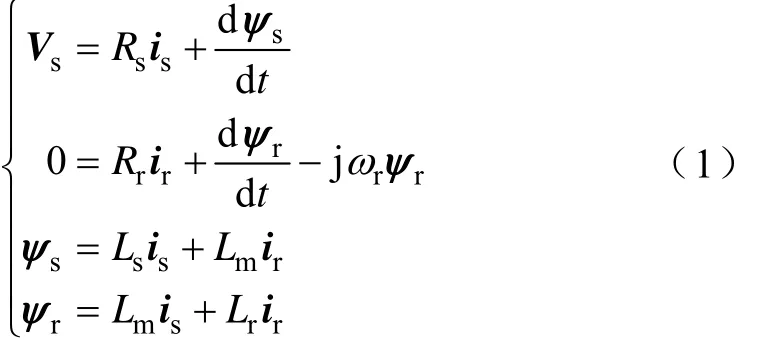
式中,Ψs和Ψr为定子和转子的磁链矢量;Vs为定子电压矢量;is为定子电流矢量;ωr为转子的电角速度;Ls和Lr为定子和转子的自感;Lm为互感;Rs和Rr为定子和转子的电阻。
由式(1)导出使用定子和转子磁链矢量作为状态变量的异步电机状态方程为

电磁转矩可以使用定子和转子磁链矢量的叉积表示为

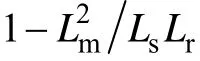
由式(3)求解转矩对时间t的微分可得

将式(2)代入式(4)中,经过推导最终得到转矩微分为

式中,⊙表示矢量点积。从式(5)可以看出转矩微分由三部分构成:第一部分与负载转矩成反比,第二部分与转速相关,最后一部分反映了定子电压矢量对转矩的影响。
当选择零电压矢量时,转矩微分变为
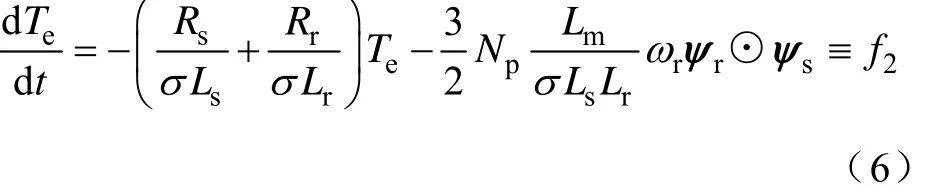
同时定子磁链的幅值可以表示为

对式(7)求导得磁链幅值对时间t的微分为
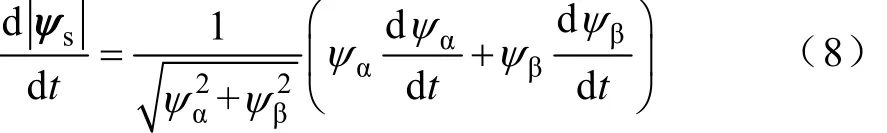
将式(2)代入式(8),推导得到磁链幅值微分为

由式(5)和式(9)可以看出,定子磁链和转矩的变化率不仅受到电压矢量的影响,而且还受到负载转矩以及电机转速的影响。基于此本文提出一个简单且非常有效的占空比确定方法,该方法对电机参数的变化具有很强的鲁棒性,并且在占空比的计算中考虑了电机转速的影响,获得了同时减小转矩脉动和其稳态误差的优良性能。

图2 逆变器电压矢量导致的转矩和定子磁链变化率Fig.2 Torque and stator flux variation rates by using each inverter voltage vector
根据式(5)和式(9)利用Matlab软件绘制在图1中给出的逆变器每个电压矢量对转矩和定子磁链变化率的影响,如图2所示,测试的异步电机参数在下表中列出。图2中电机运行在额定转矩14N·m,半额定转速750r/min状态。从图2a可以看出零电压矢量对磁链的变化率影响很小,磁链变化率为-6.552 3Wb/s,可以认为有效电压矢量增加或减小磁链变化率几乎相等。然而,对于转矩的影响比较大,为-25 094N·m/s并且总是使转矩减小,同时有效电压矢量转矩变化量为-84 643N·m/s,远远大于其增加量34 456N·m/s,如图2b所示。

表 仿真和实验参数Tab. Simulated and experimental parameters
为了深入研究转矩变化特性,根据式(5)绘制运行于不同定子磁链矢量位置,电机转速和负载条件下的转矩变化率如图3所示。以定子磁链矢量落在第1扇区为例,采样周期为100μs。

图3 定子磁链矢量位置角对应的转矩变化Fig.3 Torque variation versus stator flux vector position
从图3可以看出,转矩的变化受到电机转速的影响非常大,而受到负载变化的影响较小。甚至运行在高速区时,如图3a所示,定子磁链矢量在-30°~0°区间变化时,有效电压矢量V3引起的转矩变化率为负值,这与传统认为的有效电压矢量的作用效果恰好相反;有效电压矢量V2在定子磁链矢量在0°~30°区间变化时表现相同。零电压矢量减小转矩变化率在整个扇区都很显著,并且同样受到电机转速的影响较大。
1.3转矩稳态性能恶化的原因
在传统DTC中,滞环比较器不区分转矩和磁链误差的大小,从矢量表中选出的电压矢量将作用于整个采样周期。在转矩误差较小的周期中,转矩很快达到参考值,之后继续增大或减小,导致了较大的转矩脉动。占空比控制技术的应用可以解决这个问题。在占空比控制中,所选的有效电压矢量只在该采样周期中作用一部分时间,而剩余的时间选择零电压矢量。有效电压矢量作用时间占采样周期时间的比率称作占空比d,其取值范围是0~1。
2 新的改善转矩性能的DTC策略
综上所述,导致转矩脉动大的主要原因是滞环比较器低控制区分度和缺乏对电机转速影响的充分考虑。许多改进的DTC方法已经很好地解决了滞环比较器低控制区分率的问题[8-22],然而,这些方法或增加了系统的复杂性和参数依赖,或使转矩的稳态误差更大[18]。因此本文基于转矩脉动最小DTC方法[20]的原理,提出一个简单且非常有效的占空比确定方法,该方法在占空比计算中充分考虑电机转速的影响,获得了减小转矩脉动、同时使转矩的稳态误差更小的优良性能。
文献[20]致力于使转矩脉动的方均根值在一个采样周期中最小,如图4所示,表达式为
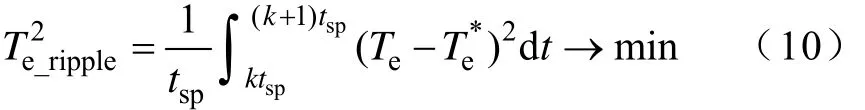

图4 经典占空比确定方法Fig.4 Principle of typical duty ratio determination method
在一个很小的采样周期tsp内,因为磁链和转速的变化相对很慢,可以假设由式(5)和式(6)计算出的有效电压矢量的上升斜率f1和零电压矢量的下降斜率f2为常数。在这种假设条件下,通过求解式(10)可得最小转矩脉动DTC占空比确定方法中有效电压矢量的作用时间为
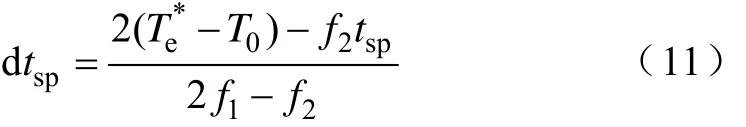
式中,f1和f2的计算非常复杂,并且严重依赖电机参数。为了消除这些缺点,期望提出一个简单占空比计算方法,该方法不仅对参数变化具有强鲁棒性,同时考虑电机转速的影响。
从图3可以看出,转矩的变化受到电机转速的影响非常大,而受到负载变化的影响较小,因此本文为了降低算法复杂性,忽略了转矩变化中负载对转矩的影响。该新型占空比确定方法的原理如下。
当εT=1时,需要增加电磁转矩,此时有效电压矢量斜率f1+和零矢量斜率f2+引起的转矩变化可以表示为
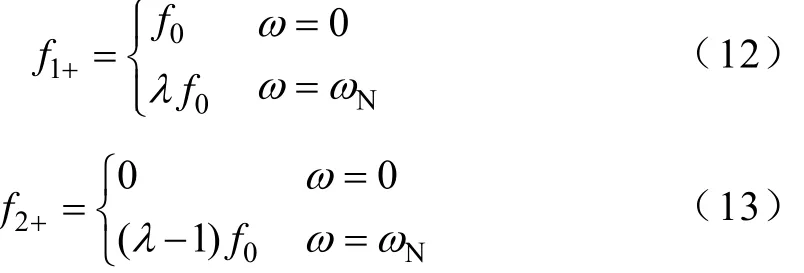
式中
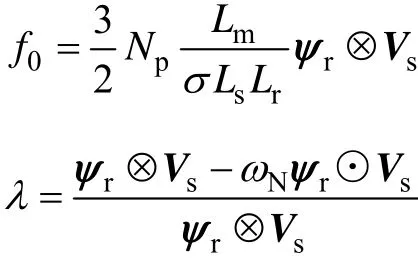
合并式(12)和式(13)得到通用表达式为

把式(14)代入式(11),得εT=1时的有效电压矢量作用时间为
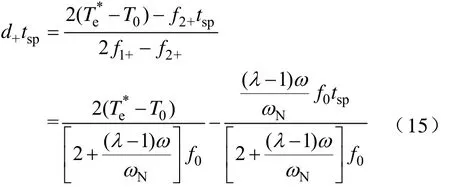
同理可得εT=-1时的通用表达式为

把式(16)代入式(11),得εT=-1时的有效电压矢量作用时间为
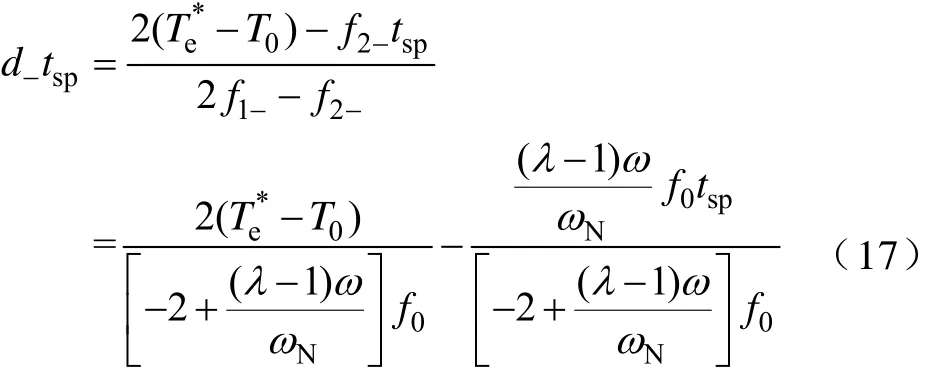
式(15)和式(17)仍然很复杂并且严重依赖电机参数,简化式(15)和式(17),得到本文提出的新型占空比确定方法表达式为

式中,λa、λb是两个正的常数,且λa=2f0tsp,λb=(1-λ)f0tsp/ωN;ΔTe为转矩误差。

确定λa的值是关键,结合图2,使用表1所列的系统参数,可得f0的取值范围为
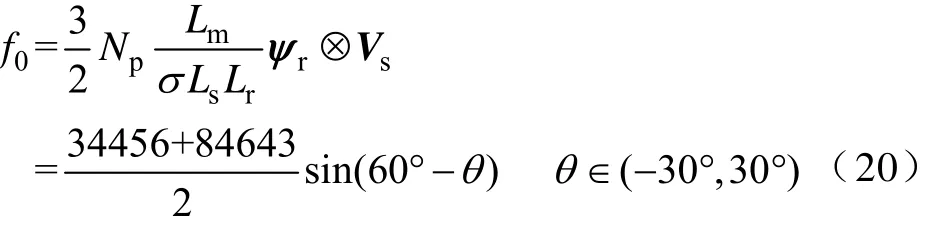
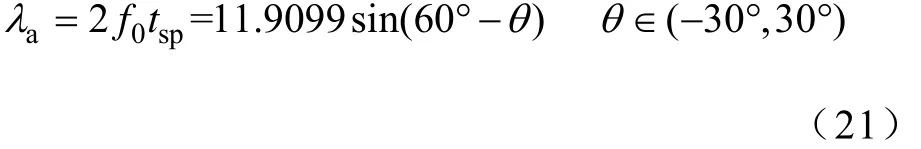
解得λa∈(5.954 95,11.909 9),一旦调制好,λa和λb就是两个固定的常数,占空比便根据转矩误差和电机转速自动调整。通过使用固定的常数λa和λb,希望新占空比确定方法受到转矩斜率计算的影响更小。需要注意的是,当转矩不处于稳态时,由式(18)计算出的d值可能超出0~1范围。当d+>1时,令d=1;当d-<0时,令d=0。
因此,可得λa的取值范围为
3 定子磁链估计
在DTC中通常使用电压模型估计定子磁链,在低速时定子电压值较小,若定子电阻值不准确,定子电阻压降的偏差对积分结果的影响会增大。本文使用基于全阶观测器的方法估计定子磁链,可以在全速域范围内准确的观测磁链。
由式(1)可构造异步电机全阶观测器的模型为

式中,Ts=Ls/Rs;Tr=Lr/Rr;G是反馈增益矩阵,G=(G1G2);上标“^”表示观测值。在观测器设计中,反馈增益矩阵G的选择是一个难点,它直接关系到观测器的收敛性和稳定性,此处将G选择为文献[23]中提出的常数增益矩阵,计算简单却很有效,即

式中,b为负的常数。
4 仿真和实验研究
4.1仿真结果
为了验证控制算法的有效性,本文首先在Matlab/Simulink中对已有方法和本文所提新方法进行仿真比较研究,以考察所提新占空比确定方法的性能。控制系统在1 050r/min运行,采样频率为10kHz,系统的外环使用PI速度控制器产生转矩参考值。转矩和磁链滞环比较器的宽度均设为零,其输出仅表明转矩和磁链误差的正、负。为了减小开关损耗,当选出的有效电压矢量是V1(100)、V3(010)和V5(001)时,紧随其后的零电压矢量为V0(000),其他情况下为V7(111)。基于新占空比控制的DTC控制系统框图如图5所示。异步电机和控制系统参数在上文表中列出。
图6给出了各种占空比控制方法与传统DTC方法的比较结果。在图6中,采用预励磁措施,电机从静止先起动至1 050r/min,并在0.3s时突加半额定负载7N·m。各种方法中转矩无论是在起动时刻还是在负载转矩突变时刻,都表现出相同迅速的转矩动态响应。其中,在稳态运行时传统DTC方法的转矩脉动最大,几乎达到了6N·m,其次是转矩脉动最小DTC方法,转矩脉动为3N·m左右,而其占空比的计算式要复杂得多。新方法与转矩和磁链同时优化DTC方法表现出相同的减小转矩脉动性能,且转矩的稳态误差更小,转矩脉动都为2N·m左右,并且通过对零电压矢量的合理选择减小了开关损耗。
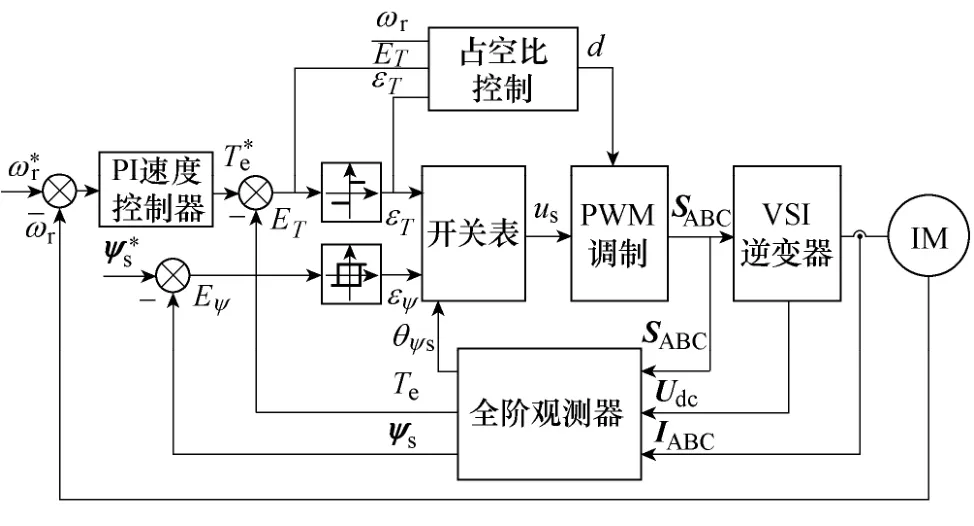
图5 新的基于占空比控制的DTC控制系统框图Fig.5 Basic block diagram of the proposed DTC system

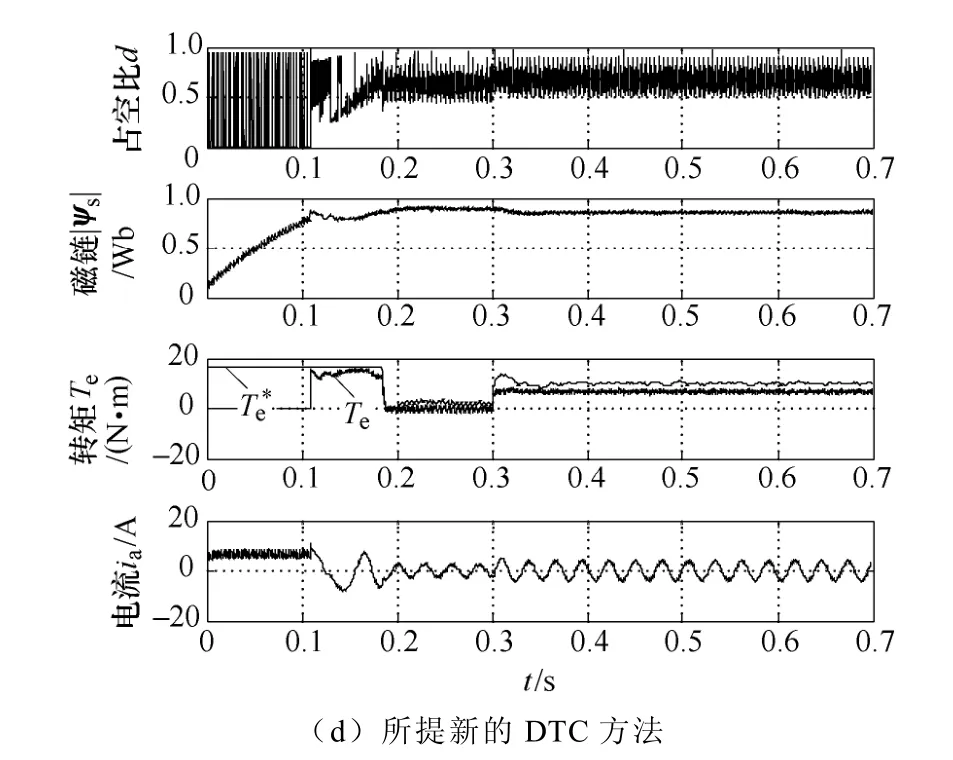
图6 各种占空比控制方法与传统DTC方法的比较Fig.6 Comparative study of various duty ratio control methods with conventional DTC
4.2实验结果
为了进一步验证本文所提新占空比控制DTC方法的可行性,在两电平逆变器馈电的异步电机驱动系统中进行了实验。为了获得较好的比较效果,实验中传统DTC方法采样频率使用20kHz,而新方法使用的采样频率为10kHz。控制器采用32位浮点DSP(TMS320F28335),可以方便地实现本文的控制算法。另外控制板上还扩展了四通道的DA输出,用于内部变量观测。实验中除电流采用电流探头直接测得外,其他变量都通过12位DA输出到示波器上显示。异步电机和控制系统参数与上表中所列相同。
首先研究系统在不同转速时的稳态性能。图7给出了传统DTC和本文所提新方法在10%额定转速和100%额定转速满载时的稳态响应波形。图中曲线从上到下依次为电机转速、电磁转矩、定子磁链和定子电流。可以看出,不论是在高速还是在低速时,基于新型占空比控制的DTC相比传统DTC的转矩脉动都有明显减小,证实了新方法的有效性。

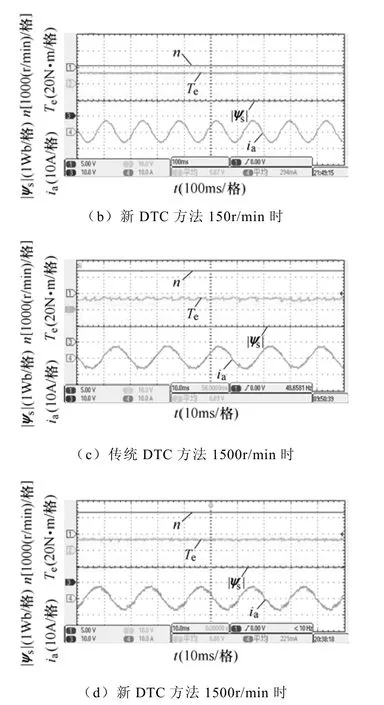
图7 电机带额定负载时稳态波形Fig.7 Steady state waveforms of 1500r/min with 100% rated load
图8给出了传统DTC和新方法在空载时从静止到1 500r/min的起动波形,比较发现两者的动态响应过程没有明显的差别,起动时间都大约为260ms,从而证明新方法保持了传统DTC方法动态响应迅速的优点。另外从图8还可以看出采用预励磁措施后起动电流峰值不超过10A,与仿真结果一致。
图9给出了电机从正转1 500r/min运行至反转1 500r/min时的实验波形,从图中转矩波形可以看出正反转响应迅速,转矩从0到100%额定转矩都约为1ms,整个正反转切换过程约持续400ms左右。证明本文所提新方法同样具有良好的动态性能。

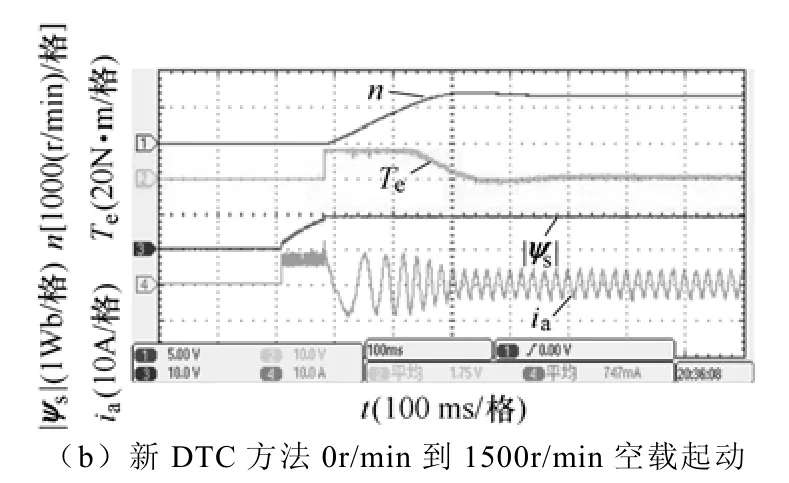
图8 0~1500r/min空载起动波形Fig.8 Experinental waveforms of starting response from 0 to 1 500r/min without load
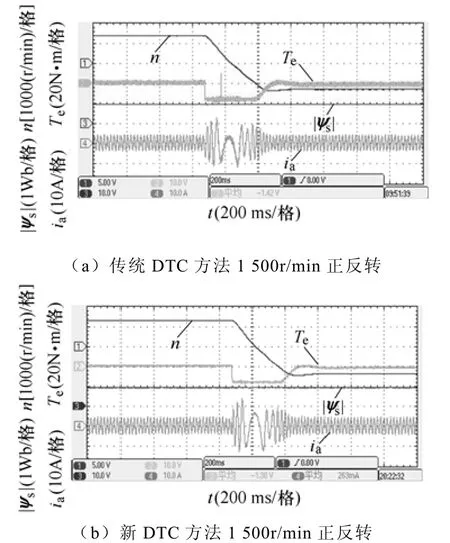
图9 电机1 500r/min正反转实验波形Fig.9 Experinental waveforms of reverse to forward operation at 1 500r/min
为考察系统对负载转矩的抗干扰能力,进行了突加、减载实验。电机先空载运行在1 500r/min,然后突加额定负载,接着又卸去全部负载,实验结果如图10所示。可以看出输出转矩响应迅速,新方法对外部负载变化同样表现出很强的抗干扰能力。
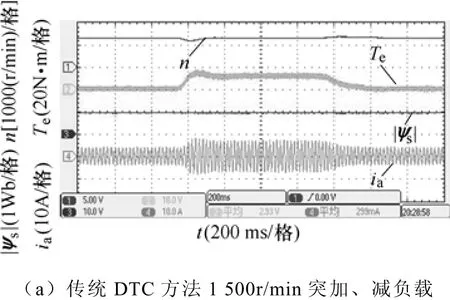
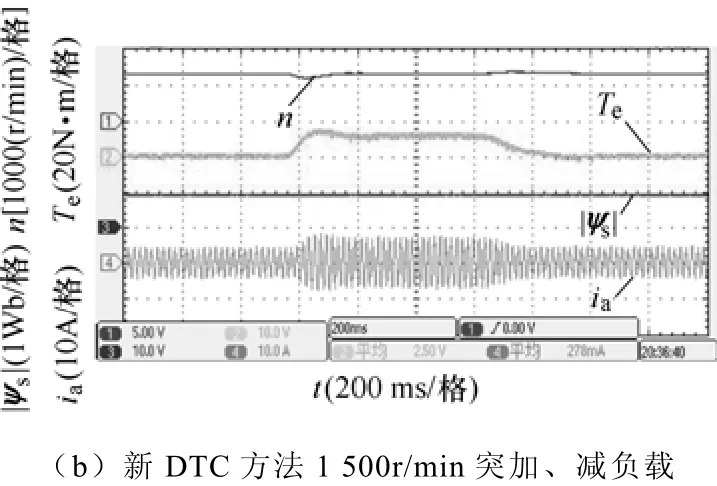
图10 负载转矩变化时的实验波形Fig.10 Experinental waveforms of response to external load disturbance
5 结论
本文在深入分析每个电压矢量导致的转矩和磁链变化率的基础上,提出一种简单且非常有效的占空比确定DTC方法,该方法保持了传统DTC的结构简单和鲁棒性强的特点。为了进一步改善系统性能,使用基于全阶观测器的方法估计定子磁链,可以在全速域范围内准确的观测磁链。仿真和实验结果表明,基于新型占空比控制的DTC方法,能明显减小转矩脉动;由于在占空比计算中考虑电机转速的影响,使输出转矩的稳态误差更小,而且保持了传统DTC响应迅速、控制简单的优点,改善了传统DTC的控制性能。
[1] Depenbrock M. Direct self-control (DSC) of inverterfed induction machine[J]. IEEE Transactions on Power Electronics,1988,3(4): 420-429.
[2] Takahashi I,Noguchi T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications,1986,22(5): 820-827.
[3] Casadei D,Profumo F,Serra G,et al. FOC and DTC:two viable schemes for induction motors torque control[J]. IEEE Transactions on Power Electronics,2002,17(5): 779-787.
[4] Buja G S,Kazmierkowski M P. Direct torque control of PWM inverter-fed AC motors—a survey[J]. IEEE Transactions on Industry Applications,2004,51(4):744-757.
[5] Tiitinen P,Surandra M. The next generation motor control method,DTC direct torque control[C]. Proceedings of the International Conference on Power Electronics,Drives and Energy Systems forIndustrial Growth,1996,1: 37-43.
[6] Ambrozic V,Buja G S,Menis R. Band-constrained technique for direct torque control of induction motor[J]. IEEE Transactions on Industry Applications,2004,51(4): 776-784.
[7] Kang J K,Sul S K. Analysis and prediction of inverter switching frequency in direct torque control of induction machine based on hysteresis bands and machine parameters[J]. IEEE Transactions on Industry Applications,2001,48(3): 545-553.
[8] Lai Yenshin,Chen Jianho. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction[J]. IEEE Transactions on Energy Conversion,2001,16(3): 220-227.
[9] Lascu C,Trzynadlowski A. Combining the principles of sliding mode,direct torque control,and spacevector modulation in a high performance sensorless ac drive[J]. IEEE Transactions on Industry Applications,2004,40(1): 170-177.
[10] Zhang Yongchang,Zhu Jianguo,Xu Wei,et al. A simple method to reduce torque ripple in direct torque-controlled permanent-magnet synchronous motor by using vectors with variable amplitude and angle[J]. IEEE Transactions on Industry Applications,2011,58(7): 2848-2859.
[11] 廖永衡,冯晓云,王珍. 基于定子磁链滑模观测器的异步电机空间矢量调制直接转矩控制[J]. 中国电机工程学报,2012,32(18): 88-97.
Liao Yongheng,Feng Xiaoyun,Wang Zhen. Induction motor direct torque control based on stator flux sliding mode observer and space vector pulse width modulation[J]. Proceedings of the CSEE,2012,32(18): 88-97.
[12] Kouro S,Cortes P,Vargas R,et al. Model predictive control—a simple and powerful method to control power converters[J]. IEEE Transactions on Industry Applications,2009,56(6): 1826-1838.
[13] Geyer T,Papafotiou G,Morari M. Model predictive direct torque control part I: concept,algorithm,and analysis[J]. IEEE Transactions on Industry Applications,2009,56(6): 1894-1905.
[14] Drobnic K,Nemec M,Nedeljkovic D,et al. Predictive direct control applied to AC drives and active power filter[J]. IEEE Transactions on Industry Applications,2009,56(6): 1884-1893.
[15] Miranda H,Cortes P,Yuz J,et al. Predictive torque control of induction machines based on state-space models[J]. IEEE Transactions on Industry Applications,2009,56(6):1916-1924.
[16] Zhu Hao,Xiao Xi,Li Yongdong. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors[J]. IEEE Transactions on Industry Applications,2012,59(2): 871-877.[17] Habetler T G,Profumo F,Pastorelli M,et al. Direct torque control of induction machines using space vector modulation[J]. IEEE Transactions on Industry Applications,1992,28(5): 1045-1053.
[18] Zhang Yongchang,Zhu Jianguo. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J]. IEEE Transactions on Power Electronics,2011,26(1):235-248.
[19] Flach E,Hoffmann R,Mutschler P. Direct mean torque control of an induction motor[C]. Proceedings European Power Electronics and Applications (EPE),Trondheim,Norway,1997: 672-677.
[20] Kang J K,Sul S K. New direct torque control of induction motor for minimum torque ripple and constant switching frequency[J]. IEEE Transactions on Industry Applications,1999,35(5): 1076-1082.
[21] Romeral L,Arias A,Aldabas E,et al. Novel direct torque control (DTC) scheme with fuzzy adaptive torque-ripple reduction[J]. IEEE Transactions on Industry Applications,2003,50(3): 487-492.
[22] 杨家强,黄进. 异步电动机直接转矩控制转矩脉动最小化方法研究[J]. 电工技术学报,2004,19(9): 23-29.
Yang Jiaqiang,Huang Jin. Research on torque ripple minimization strategy for direct torque control of induction motors[J]. Transactions of China Electrotechnical Society,2004,19(9): 23-29.
[23] Zhang Yongchang,Zhu Jianguo,Zhao Zhengming,et al. An improved direct torque control for three-level inverter-fed induction motor sensorless drive[J]. IEEE Transactions on Power Electronics,2012,27(3):1502-1513.
A Novel Direct Torque Control Strategy of Induction Machine Drives with Simple Duty Ratio Calculation
Li Zhengxue1Zhang Yongchang2Li Zhengxi2Ban Xiaojuan1Yang Haitao2
(1. University of Science and Technology BeijingBeijing100083China
2. Power Electronics and Motor Drivers Engineering Research Center of Beijing North China University of TechnologyBeijing100144China)
The traditional switching-based direct torque controlled (ST-DTC) induction motor drive is usually affected by large torque ripple and steady-state error of torque. The existing literature has proposed some methods to reduce torque ripple by optimizing the duty ratio of the active vector. However,these methods are usually complicated and depend heavily on motor parameters. Based on the analysis in instantaneous variation rates of stator flux and torque caused by each voltage vector,a simple and effective method considering the effect of machine velocity is proposed to acquire the duty ratio. The proposed scheme is able to reduce the torque ripple and steady-state error of torque significantly,while maintaining the simplicity and robustness of the traditional DTC at the most. Simulations and experimental results validate the proposed scheme.
Direct torque control,induction motor,ripple reduction,duty ratio,steady-state error
TM343;TM921
李政学男,1976年生,博士研究生,讲师,研究方向为电力电子与电机控制。
张永昌男,1982年生,博士,副教授,硕士生导师,研究方向为电力电子变换器、电机控制和新能源发电。
国家自然科学基金资助项目(51207003、51347004)。
2014-04-09改稿日期 2014-04-30

