运算式电容测微仪解调滤波器动态特性优化
赵树忠,李 科
(河北联合大学,河北 唐山 063009)
0 引 言
基于变极距式电容传感器的电容测微仪具有分辨率高、准确度高、非接触测量等诸多优点,因此在各种工业领域及科学研究领域得到了广泛的应用,适用于位移的静态测试以及振动、跳动、回转运动误差的动态测试。运算式电容测微仪采用运算式测量电路,不仅从理论上极大地改善了输入与输出的非线性关系,并且通过幅值调制使整机易于实现不失真测试,因此目前国内外大部分电容测微仪均采用运算式原理[1]。国外的同类电容测微仪如英国Queensgate Instruments公司生产的纳米定位系统SYSTEM 2000中的NS2000电容测微仪,其动态测量范围已达5kHz。为了改善国产电容测微仪的动态特性,扩展动态测量范围,在对整机动态特性影响最大的解调滤波器进行动态特性理论分析的基础上,优化滤波器的参数,使其动态特性在指定的频率范围内基本满足不失真测试条件,动态测量的频率范围得到扩展。
1 仪器工作原理

图1 运算式电容测微仪的工作原理
图1为运算式电容测微仪的工作原理示意图[1]。变极距式电容传感器将被测信号的变化转换成传感器电容CT的变化,传感器电容CT作为调制信号,与放大器A、参比电容C0、高频稳幅交流电源ui(载波)一起对被测信号进行幅值调制,输出uo为高频调幅信号。由于CT的变化是单极性的,因此其解调通过精密整流和低通滤波两个环节即可实现。
其工作原理的主要特点是:交流放大器的零漂小,有利于信号的精确转换与调制;通过比例运算使放大器输出调幅信号的幅值与被测信号幅值(传感器两极板间距)在理论上呈线性关系,有利于提高整机的线性范围,改善线性度和测量精度;解调电路简单,不需要相敏检波,有利于获得所需的动态特性。
2 解调滤波器的动态特性分析
2.1 解调滤波器的组成
图2为运算式电容测微仪中的解调滤波器,它由一个带阻(陷波)滤波器和两个低通滤波器串联而成[2-3]。这几个滤波器不仅要滤除精密整流后信号中的高频载波以及其他干扰成分,其动态特性还要最大限度地接近不失真测试条件,为整机提供足够的通频带。

图2 解调滤波器
2.2 带阻滤波器的动态特性
带阻滤波器的作用是最大限度地滤除高频载波。由于使用无限增益多路负反馈型电路不能构成带阻滤波器,因此带阻滤波器在结构上采用了压控电压源型二阶有源滤波电路[4]。在双T网络后增加了一个小电容C4(接地),可以使中心频率附近的幅频特性值较小、通带内的相频特性值较小。通过输出的反馈,可以使阻带沿较陡、带宽较小,有利于提高滤波器的选择性和品质因数[5]。
对于由双T网络与C4构成的带阻滤波器[6],反馈系数F=R5/(R4+R5),若取R1=R2=R,C1=C2=C,则其传递函数为


2.3 低通滤波器的动态特性
两个低通滤波器[4]的作用是进一步滤除残余的高频成分,使整机具有一定的通频带。考虑到它们应具备较好的稳定性且结构应尽可能简单,因此采用了结构相同的无限增益多路负反馈二阶有源滤波电路。利用多路负反馈来削弱反馈电阻(R7和R11)在其固有频率处的反馈作用,再通过匹配两个滤波器的参数,使滤波器的特性更接近理想滤波器。两低通滤波器的传递函数分别为


其中 R02=R6‖R7‖R8,R03=R10‖R11‖R12。它们的固有频率fn1和fn2、阻尼比ξ1和ξ2分别为

3 解调滤波器动态特性的优化
以上述滤波器动态特性的理论分析为基础,针对仪器的实际工作条件(被测信号频率范围0~2 kHz,载波频率21kHz)[7]对与滤波器动态特性有关的元件参数进行初步设计。在选择滤波器元件的具体参数数值时,做了如下考虑:
1)解调滤波器总体的幅、相频特性应尽可能接近不失真测试条件。
2)精密整流后信号中交流成分的基频约为42 kHz,因此带阻滤波器的中心频率也应设定在此频率左右[8]。由于该中心频率远远高于所需要的低通滤波器的上截止频率,故整个解调滤波器的动态特性基本取决于两个低通滤波器的动态特性。
3)为使两个低通滤波器串联的效果接近于理想的低通滤波器,将低通滤波器1设计成ξ1>0.707,低通滤波器2设计成ξ2<0.707,使两低通滤波器的幅频特性相乘后具有通带较宽、在通带内的幅频特性较平坦、相频特性值与频率接近比例关系、过渡带的衰减速率大、选择性好等特性(见图3)。将低通滤波器1设计成ξ1>0.707是为避免仪器工作时放大器A2饱合。通过适当设置两个滤波器的固有频率、阻尼比,可以达到此目的[9-10]。

图3 低通滤波器的频率特性
4)由式(5)及式(6)可知,两个低通滤波器的固有频率和阻尼比分别取决于 R6、R7、R8、C5、C6和 R10、R11、R12、C7、C8。通过调整这些参数可以优化解调滤波器的动态特性。值得注意的是,这些参数同时对固有频率和阻尼比产生影响,存在相互矛盾的现象。因此,在初步设计出的参数数值基础上,根据式(5)及式(6),采取边调整参数数值、边用Matlab仿真观察幅频和相频特性结果的技术路线,同时通过对特性的实际测试验证优化的效果。图4为动态特性测试实验的框图。

图4 动态特性测试实验框图
从图中可知,先由信号发生器提供某一频率的正弦信号作为滤波器的输入ui(幅值为3V),然后用精密数字电压表测出输出uo的幅值,输出与输入的幅值比即为滤波器在该频率下的幅频特性值A(f)。如此,在0~42kHz的频率范围内对若干个频率点的幅频特性值进行测试,就得到了在目前参数组合下滤波器的动态特性。经过反复的参数调整、动态特性测试实验,最终确定使滤波器动态特性接近预期特性的优化参数组合:

最终测试出的滤波器动态特性如表1所示。
根据实测结果可知,由于元件参数的分散性和运算放大器的非理想性,滤波器的实际特性与理论特性存在一定差异。实际电路的截止频率约为6kHz(归一化后的幅频特性为 1.120/1.576≈0.71),其后幅频特性衰减很快,在42kHz处基本上已经接近零。在频率低于2 kHz的范围内,幅频特性的波动不超过3%,基本满足了不失真测试条件的要求。
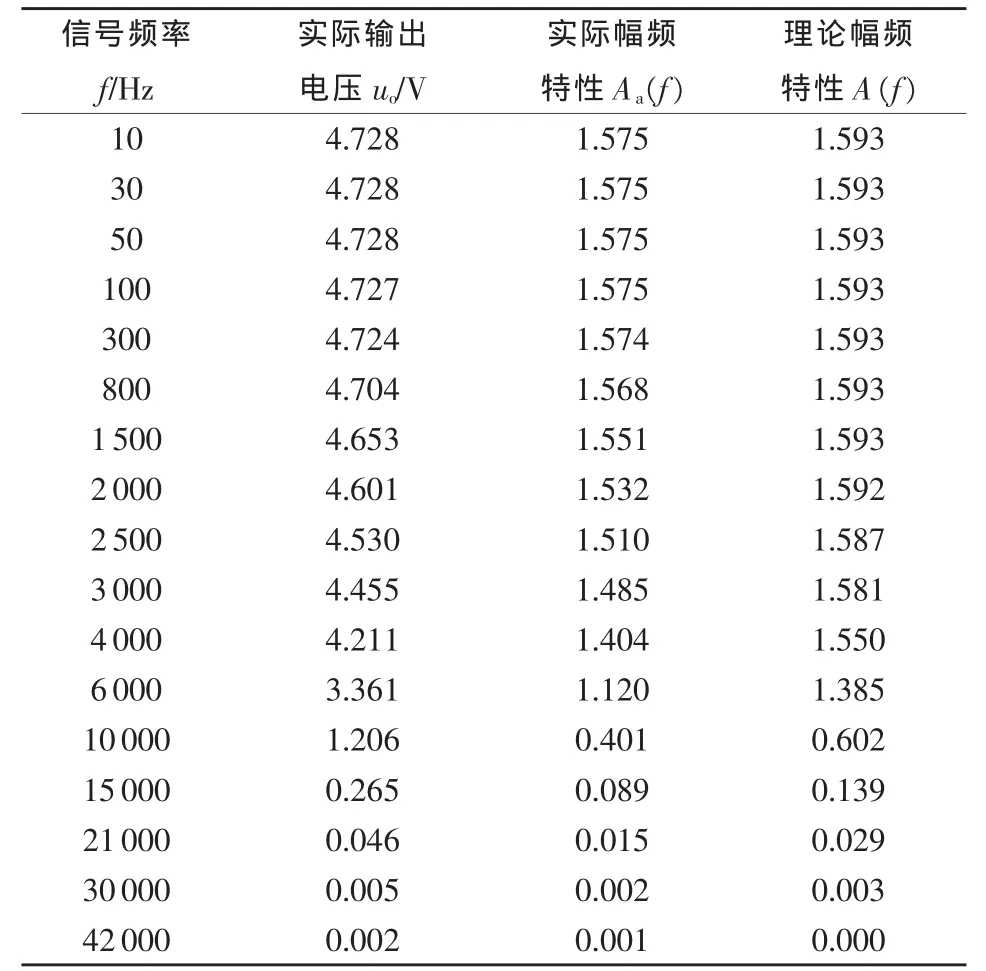
表1 动态特性测试结果
4 结束语
解调滤波器位于运算式电容测微仪的最后环节,其动态特性对整机的动态特性有着很大的影响,通过对其动态特性的理论分析并借助Matlab仿真、实验测试,确定出了优化的元件参数,使解调滤波器的动态特性达到预期的要求,实现扩展运算式电容测微仪的动态测试范围、改善线性度、提高仪器精度的目的。
[1]赵树忠,郑义忠.改进电容测微仪稳定性的技术措施[J].中国测试技术,2003,29(5):7-9.
[2]张宇华,王晓琳.电容测微仪动态特性的改进及标定方法[J].北京理工大学学报,1999(1):87-91.
[3]赵晋云,樊玉铭,张国雄.智能电容测微仪系统[J].电子测量技术,2005(4):11-12.
[4]张国雄.测控电路[M].北京:机械工业出版社,2000:19-97.
[5]刘宇.微型化数字式电容测微仪的研究[D].天津:天津大学,2007.
[6]赵晋云.智能电容测微仪系统关键技术的研究[D].天津:天津大学,2005.
[7]李建文,刘书亮,郑义忠.高精度电容测微仪关键技术[J].天津大学学报:自然科学版,2004,37(9):787-791.
[8]张洪刚.高精度电容测微仪关键技术的研究[D].天津:天津大学,2000.
[9]朱义强,邓湘,崔桂利.精密振动测量用动态滤波器设计[J].电子测量与仪器学报,2009,23(1):52-57.
[10]Testuya O,Hirofumi M.Analysis of dynamic characteristics for the Partially Resonant Active Filter with the DSP[J].IEICE Transactions on Communications,2007,E90-B(9):2562-2570.

