三自由度液压伺服机械手轨迹优化

刘湘琪，蒙 臻，倪 敬，朱泽飞

（1.浙江理工大学机械与自动控制学院，浙江杭州310018；2.杭州电子科技大学机械工程学院，浙江杭州310018）

三自由度液压伺服机械手轨迹优化

刘湘琪1，2，蒙 臻1，倪 敬2，朱泽飞2

（1.浙江理工大学机械与自动控制学院，浙江杭州310018；2.杭州电子科技大学机械工程学院，浙江杭州310018）

采用闭链矢量运动学模型，引入5阶B样条曲线插值逼近理论，提出一种基于非轴系驱动空间的液压机械手运行轨迹规划算法.针对当满足运动学约束时机机械手的总运行时间优化问题，引入改进型粒子群优化算法，优化求解时间步长，从而实现时间最优连续运动轨迹曲线.实际应用的实验结果显示：可以将实际工具中心点（TCP）轨迹和期望轨迹的绝对误差控制在25 mm以内，为液压机械手运动控制提供较理想的轨迹曲线.该研究较好地解决了非关节驱动液压机械手系统运动规划问题，提高了针对复杂路径规划算法的效率.

闭链模型；轨迹规划；B样条曲线；粒子群优化算法

基于电液伺服控制的多自由度液压机械手，具有负载刚性大、功率重量比大、耐温性强、使用维护方便等特点，广泛应用于大功率负载搬运的场合［1］.在应用过程中，对于液压伺服机械手运行精度和生产效率的要求愈加提高，即机械手高速、精确的运动变得十分重要［2］，因此，为了实现液压机械手高效、高精度的运转，同时保证其运行平稳性，研究液压伺服机械手轨迹规划算法具有重要的实际意义.

机械手的轨迹规划问题即根据给定的几何路径寻求运动学模型［3］.Abe［4］基于两连杆串联机构的运动学模型，研究了机械手执行末端轨迹规划问题.朱世强等［5］基于六自由度串联机械手的运动学模型，研究了速度、加速度和脉动均连续的关节轨迹.周芳等［6］基于六自由度检修机械手的运动学模型，研究了所规划轨迹的安全性.在上述研究中，国内外学者主要基于常规开链式结构的机械手，采用De-navit-Hartenberg（D-H）法构造轨迹运动学模型.在实际应用研究中，由于多自由度液压机械手的闭链式结构和非独立轴系驱动形式，导致各关节的运动学空间具有较强的耦合作用，采用常规轨迹运动学模型较难求解液压机械手运动轨迹，研究适用于液压机械手的轨迹运动学模型显得十分必要.

关于机械手的轨迹规划算法不断涌现.Gasparetto等［7］同时采用了三次样条插值函数与5阶B样条插值函数推导轨迹算法，并探讨了轨迹执行时间最优与轨迹光滑性最优的权重问题.Tian等［8］采用基于Hermite三次样条插值函数的方法规划机械手轨迹，并基于遗传算法优化轨迹插值函数.Bauml等［9］研究了机器人实现抓取任务的问题，提出了基于梯形速度曲线的空间轨迹规划方法.Saravanan等［10］使用NURBS曲线规划运动轨迹.徐海黎等［11］采用三次多项式曲线构建机器人轨迹，通过使用加权系数的代价函数，计算优化轨迹总动作时间和总消耗能量的权重.杨玉维等［12］基于拉格朗日原理构建系统动力学模型，通过线性迭代法（iterative linear programming，ILP），规划出运动时间最优化轨迹.史也等［13］采用量子粒子群优化算法，基于参数化的关节轨迹函数，实现空间机器人轨迹规划目标.Guo等［14］采用量子粒子群算法进行平面冗余机械臂避碰轨迹规划.张书涛等［15］提出基于Tau理论的仿生轨迹规划方法.戈新生等［16］基于傅里叶基函数，通过对其系数组成的向量进行优化，提出了一种应用粒子群优化的最优运动规划数值算法.上述研究所涉及的应用模型主要集中于常规机械手，其驱动空间通常位于相对独立的关节轴系上，可通过D-H法将末端位置矢量转化到驱动空间上.在实际研究中，液压机械手驱动空间位于非关节轴系的组合连杆上，通过闭链式机构驱动末端动作，采用常规轨迹规划方法较难解出平滑的运动轨迹，因此研究适用于多自由度液压机械手的轨迹规划方法显得十分必要.

本文以三自由度（degrees of Freedom，DOF）的液压伺服机械手系统为例，基于闭链矢量运动学模型，引入非轴系驱动空间的5阶B样条插值方法构建轨迹，采用改进型粒子群优化算法来优化轨迹的总动作时间，并通过实验结果说明该轨迹规划方法的有效性.

1 机械手机构运动学模型

三自由度液压伺服机械手主要由回转系统、俯仰系统和推拉系统组成，如图1所示.其中：回转系统主要由回转液压马达实现机械手工具中心点（tool center point，TCP）绕Z轴转动（O-X-Z为侧视坐标系，O-X-Y为俯视坐标系）；俯仰系统由俯仰液压缸驱动，可实现TCP沿Z轴运动，附带沿着X轴运动；推拉系统由推拉液压缸驱动实现TCP沿X轴运动，附带沿着Z轴运动.

图1 三自由度液压机械手结构图Fig.1 Configuration of hydraulically driven 3DOF manipulator

为了精确描述工作空间中的TCP位置矢量，同时考虑机械手运动学分析的完备性，可将3DOF液压伺服机械手的运动模型简化为如图2所示，Ob-Xb-Yb-Zb为机械手基座坐标系，Ot-Xt-Yt-Zt为机械手工具坐标系，其中基座标系原点Ob与机械手基座回转中心重合，工具坐标系原点Ot与TCP重合.各杆件的铰接点由Pi表示（i＝1，2，…，10）.如图2所示的机械手系统具有闭式连杆机构特性和非轴系驱动的运动特性，若采用常规D-H法求解运动学问题会因冗余铰接点产生非唯一解，因此采用几何矢量解析法求解3DOF液压伺服机械手运动学问题.

根据杆件封闭矢量方程可得

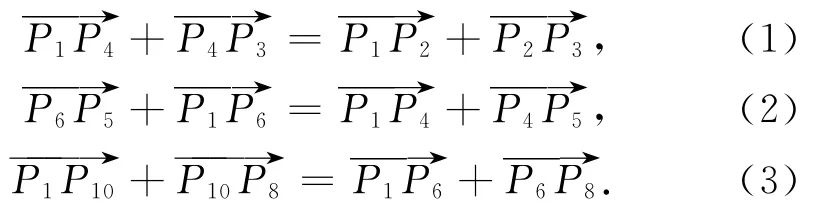
基于矢量平行或共线的特性可得

图2 3DOF液压机械手立面图Fig.2 Elevation of hydraulically driven 3DOF manipulator

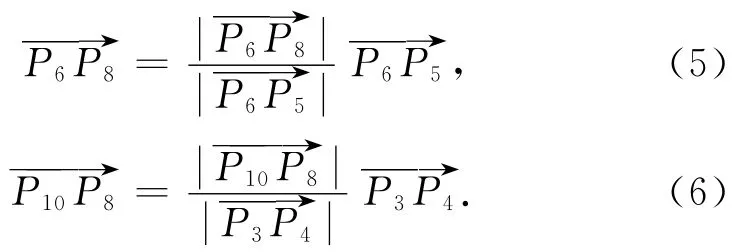
TCP位置矢量与基座标系的矢量关系为

将式（1）～（6）代入式（7）可得

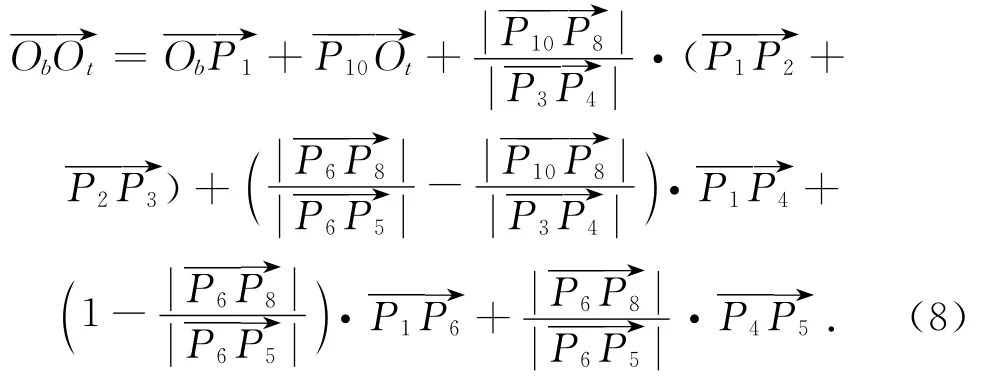
将式（8）用复数形式可表示为

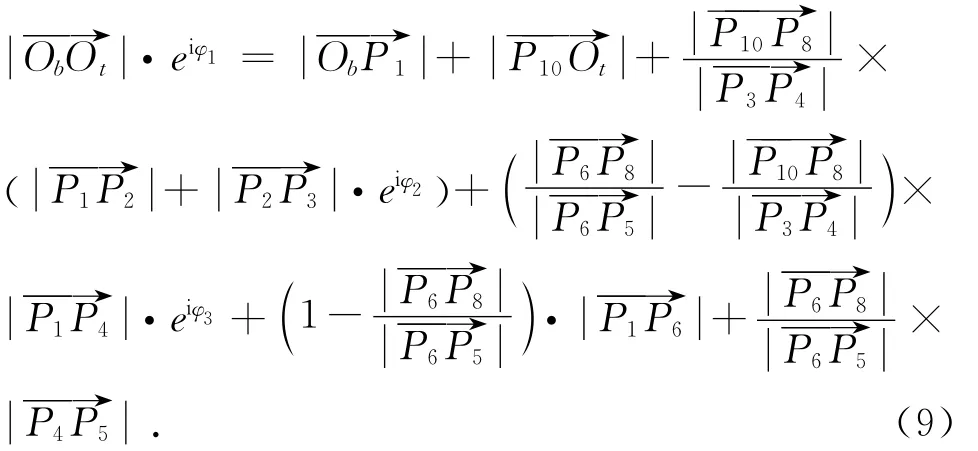
将式（9）按欧拉公式展开可得

式中：

令r＝［xt，yt，zt］T，x＝［x1，x2，θ］T，其中x1为推拉系统的输出位移，x2为俯仰系统的输出位移，θ为回转系统的输出位移，则TCP空间位置r可根据式（8）表示为

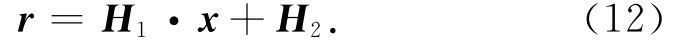
式中：

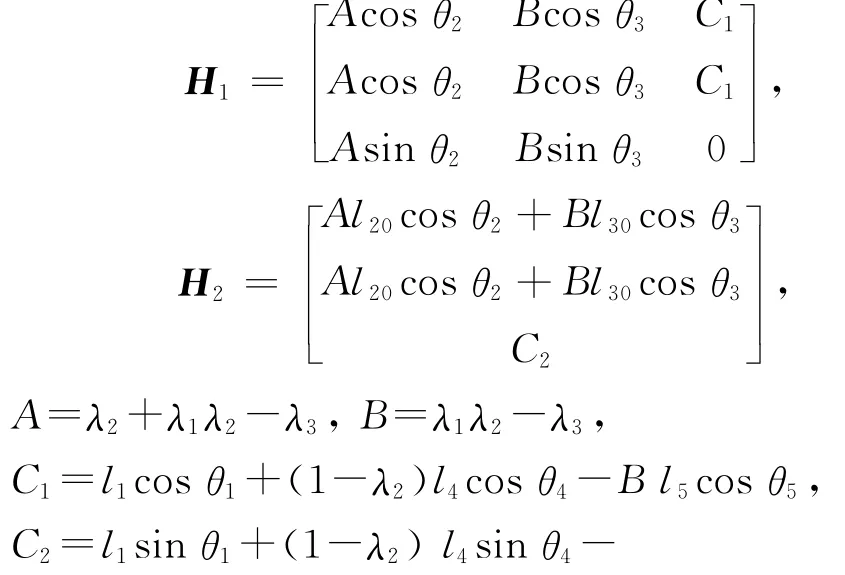
B l5sinθ5，l20、l30分别为l2、l3的初始长度.

2 机械手轨迹优化

2.1 基于B样条的轨迹规划

液压机械手的轨迹S由工作空间中一系列离散的TCP空间位置序列rp和相应的时间节点序列tp组成.为了精确描述驱动输入x与轨迹S的映射关系，根据TCP空间位置模型，通过逆运动学求解，将TCP空间位置序列rp转换为驱动空间节点位置序列xp，k，进而构成驱动节点-时间序列：

式中：p＝0，1，…，n，k＝0，1，2.

基于轨迹S的连续性要求，用C3连续的4次（5阶）B样条曲线构造驱动节点轨迹.所有节点轨迹曲线统一描述为

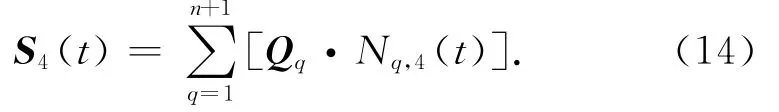
式中：Qq∈RN×1为控制顶点矢量，q＝1，2，…，n＋1，t为通过相邻控制顶点所用的时间维度，Nq，4（t）为4次B样条基函数：

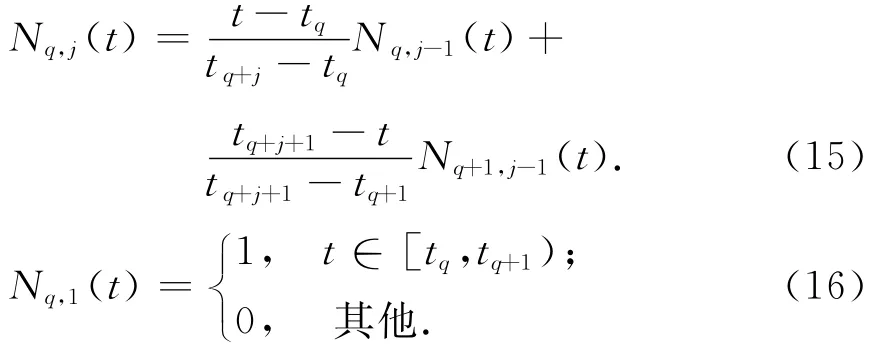
其中，j＝2，3，4.

基于De Boor递推关系［6］，t（t∈［tq，tq＋1］）处的节点速度、加速度和脉动分别与B样条轨迹曲线的l阶导数（t）对应，l＝1，2，3.

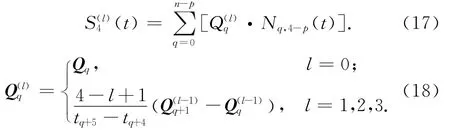
由式（17）、（18）可知，节点速度轨迹曲线V4（t）、加速度轨迹曲线A4（t）和脉动轨迹曲线J4（t）可分别表示为

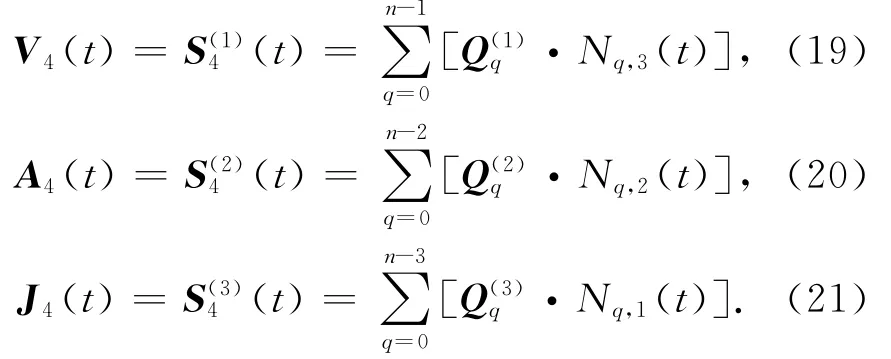
根据样条插值特性，节点轨迹插值函数满足以下条件：

由式（19）可以列出3（n＋3）个方程，为了求解式（14）中产生的3（n＋4）个未知控制顶点矢量Qq，还需3个边界条件，假设节点初始条件为

式中：t0为上述时间维度的起点.联立式（14）～（22），以矩阵方程的形式描述第k个驱动节点的轨迹曲线控制顶点矢量反求方程：

式中：系数矩阵Mk∈R（n＋4）×（n＋4），控制顶点矩阵

Qk＝［Qk，0，Qk，1，…，Qk，n＋3］T，位置序列矩阵xk＝［xk，0，xk，1，…，xk，n，v0，a0，J0］T.

由式（24）可以求出4次B样条轨迹曲线的控制顶点矢量，进而求出驱动节点在时刻ti经过位置xi的C3连续节点轨迹.

2.2 基于粒子群的轨迹优化

在轨迹规划过程中，通常既要满足运动学约束，保证轨迹的平滑性，又要降低轨迹的总运行时间，保证机械手运行效率.为了综合权重轨迹的平滑性和执行时间，采用B样条轨迹的通用优化目标函数［4］：

式中：hq表示相邻节点步长，hq＝tq＋1－tq；tf表示轨迹总执行时间；kT表示时间权重系数，kJ表示脉动权重系数（kT＝0，可得到最平滑的轨迹；kJ＝0，可得到执行最快的轨迹）.式（23）中脉动平方的积分项其结构复杂，较难解析，通常直接采用数值积分程序（如Matlab中的Quadl函数），或者可先通过递归De Boor公式确定基函数的解析表达式，再积分求解，最终获得积分表达式.

实际上，在优化求解过程中，为了降低计算量，可将kT、kJ及脉动平方积分项设定为确定值，因此，可将B样条轨迹的优化问题转化为对hi的优化.

受改进型粒子群算法的启发，将时间步长hi视作粒子，通过修改惯性权重参数追踪最优粒子，迭代搜索全局最优解，从而求解式（25）描述的路径点时间步长hi优化问题，具体优化过程如下［17-18］.

1）选取相邻节点时间步长hu为粒子，第u个粒子的位置矢量为xu＝［hu1，hu2，…，huD］T，其速度矢量为vu＝［vu1，vu2，…，vuD］T.它的个体极值为Pu＝［Pu1，Pu2，…，PuD］T，种群的全局极值为Pg＝［Pg1，Pg2，…，PgD］T，D为粒子维度，其中，粒子群的优化方向可由式（25）表示.

2）初始化粒子的位置和速度，所选择的位置和速度具有一定的随机性.

3）根据式（26），更新每个粒子的速度和位置：

式中：u＝1，2，…，N，N为粒子总数；d＝1，2，…，D；为第k次迭代粒子u速度矢量的d维分量；为第k次迭代粒子u位置矢量的d维分量；pud为粒子u在d维的个体极值点位置pbestu；pgd为群体在d维的全局极值点位置gbest；c1、c2为加速因子；rand（）为［0，1.0］的随机数；w为惯性因子.

4）获得最优解.按照如图3所示的程序流程依次迭代得到最优解h，根据式（26）调整粒子的速度和位置，如果达到最大迭代次数M或最优解停滞不再发生变化，则终止迭代；否则回到步骤2）.

图3 粒子迭代优化程序Fig.3 Particle iterative optimization procedure

3 实验与分析

3.1 仿真实验

为验证上述方法的有效性，以如图2所示的机械手模型为基础，采用Matlab／Sim Mechanics建立机械手运动学模型，以对液压机械手轨迹规划方法进行仿真验证.机械手TCP经过的空间位置序列及逆解驱动节点位置序列如表1所示，驱动节点动力学约束条件如表2所示.表中，x1为推拉系统的输出位移，x2为俯仰系统的输出位移，θ为回转系统的输出位移.

表1 空间位置序列及驱动节点位置序列Tab.1 Space position sequence and position sequence of drive node

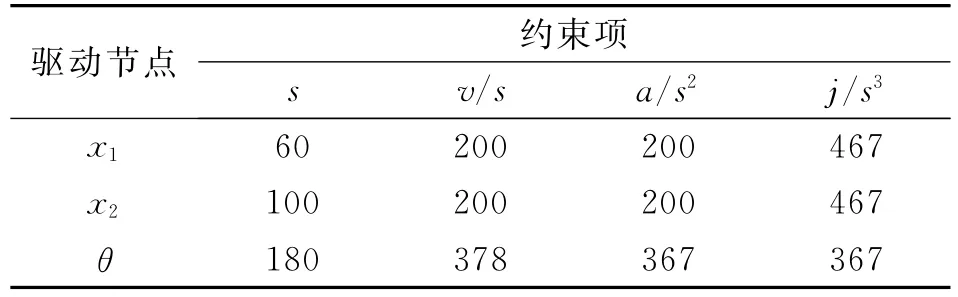
表2 机械手运动学约束条件Tab.2 Manipulator kinematics constraint conditions

采用2.1节的插值轨迹规划及时间步长优化算法，经过33次迭代规划后，终止迭代.其中，时间步长hi的优化过程如图4所示；第0次、第10次及第23次迭代后，时间步长hi的优化结果如表3所示.各驱动节点轨迹迭代优化前、后，机械手仿真TCP轨迹如图5所示.

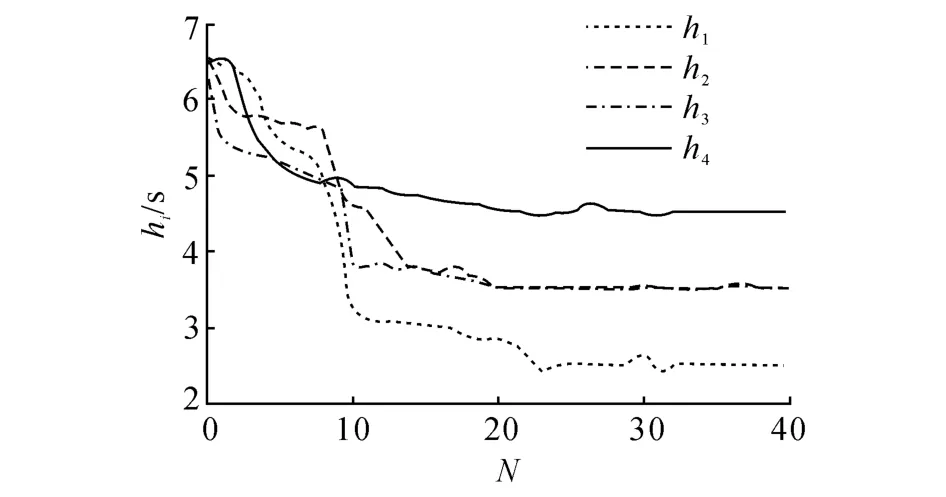
图4 各时间步长粒子优化过程Fig.4 Particle optimization process of each time step

图5 迭代前、后的TCP轨迹图Fig.5 TCP trajectory before and after iteration

表3 各节点运动时间对比Tab.3 Comparison of movement time period of each joint s

3.2 系统实验

实验用3DOF液压机械手系统如图6所示，主要工况及元件包括液压油源工作压力（8 MPa）、工作流量（100 L／min）、液压马达A2FM56／61W、液压缸Φ50／（36～100）mm、绝对位置旋转编码器E6B2-C、力士乐比例伺服阀4WRZE10-75、脉冲计数模块、DA模块以及研华工控机，具体实验步骤如下.

1）实验工况选取.实际3DOF液压机械手系统的运行参数与表1、表2所示一致.为了便于观测，设定机械手TCP起点为r0＝［790，0，425］T，目标点为rg＝［0，1 268，755］T.

2）机械手轨迹规划及优化.采用插值轨迹规划及时间步长优化算法，基于3.1节中的轨迹规划及优化步骤拟合系统实验所需的驱动节点轨迹.

3）运行结果分析.为了观测轨迹规划效果，本实验采用常规PID控制（只选取了比例参数为1.8.基于3.1节中第23次迭代后的期望轨迹，对各驱动节点轨迹进行跟踪控制，最终实现如图7所示的TCP轨迹.由图7可知，由于液压伺服系统的非线性因素及实际机构装配间隙等，实际TCP轨迹相比期望轨迹球面绝对误差小于25 mm.本方法所规划的机械手轨迹相对平滑，有利于机械手的控制；而且规划的路径中考虑机械手位置、速度、加速度和脉动的限制，使算法更具有实用价值.

图6 3DOF液压机械手现场实物图Fig.6 Picture of hydraulically driven 3DOF manipulator

图7 液压机械手TCP运行轨迹Fig.7 TCP trajectory of hydraulically driven manipulator

4 结 论

（1）提出了基于闭链矢量机构的液压机械手运动学模型，将机械手TCP空间位置矢量解析为驱动节点空间位置矢量，使液压机械手运动学建模方法更具实效性.

（2）提出了基于5阶B样条插值曲线的液压机械手轨迹规划方法，应用C4连续性特性，推导了液压机械手驱动节点轨迹规划公式，令液压机械手的运动学约束转化为轨迹曲线的控制顶点约束，提高了液压机械手轨迹规划方法的通用性.

（3）提出了基于改进粒子群优化算法的液压机械手轨迹时间最优规划问题，改进了常规轨迹规划算法难以保证全局收敛、收敛速度慢等问题，可以较快地找到最优解，在解决复杂优化问题方面计算效率更高.

（4）仿真和应用实验表明：所提出的液压机械手轨迹规划方法，可以较好地解决非关节驱动液压机械手系统运动规划问题，验证了轨迹规划算法的有效性.同时，本研究对于工业液压机械手运动控制及轨迹优化有参考意义.

（References）：

［1］潘楚滨.液压与气压传动［M］.北京：机械工业出版社，2010：108- 110.

［2］GASPARETTO A，LANZUTTI A，VIDONI R，et al.Experimental validation and comparative analysis of optimal time-jerk algorithms for trajectory planning［J］.Robotics and Computer-Integrated Manufacturing，2012，28（2）：164- 181.

［3］GASPARETTO A，ZANOTTO V.Optimal trajectory planning for industrial robots［J］.Advances in Engineering Software，2010，41（4）：548- 556.

［4］ABE A.Trajectory planning for residual vibration sup-pression of a two-link rigid-flexible manipulator considering large deformation［J］.Mechanism and Machine Theory，2009，44（9）：1627- 1639.

［5］朱世强，刘松国，王宣银，等.机械手时间最优脉动连续轨迹规划算法［J］.机械工程学报，2010，46（3）：47- 52.

ZHU Shi-qiang，LIU Song-guo，WANG Xuan-yin，et al.Time-optimal and jerk-continuous trajectory planning algorithm for manipulators［J］.Journal of Mechanical Engineering，2010，46（3）：47- 52.

［6］周芳，朱齐丹，赵国良.基于改进快速搜索随机树法的机械手路径优化［J］.机械工程学报，2011，47（11）：30- 35.

ZHOU Fang，ZHU Qi-dan，ZHAO Guo-liang.Path optimization of manipulator based on the improved rapidlyexploring random tree algorithm［J］.Journal of Mechanical Engineering，2011，47（11）：30- 35.

［7］GASPARETTO A，ZANOTTO V.A new method for smooth trajectory planning of robot manipulators［J］.Mechanism and Machine Theory，2007，42（4）：455- 471.

［8］TIAN L F，COLLINS C.An effective robot trajectory planning method using a genetic algorithm［J］.Mechatronics，2004，14（5）：455- 470.

［9］BAUML B，WIMBOCK T，HIRZINGER G.Kinematically optimal catching a flying ball with a hand-arm-system［C］∥IEEE／RSJ International Conference on Intelligent Robots and Systems（IROS）.Taipei：IEEE／RSJ，2010：2592- 2599.

［10］SARAVANAN R，RAMABALAB S，BALAMURUGAN C.Multi-objective trajectory planner for industrial robots with payload constraints［J］.Robotica，2008，26（6）：753- 765.

［11］徐海黎，解祥荣，庄健，等.工业机器人的最优时间与最优能量轨迹规划［J］.机械工程学报，2010，46（9）：19- 25.

XU Hai-li，XIE Xiang-rong，ZHUANG Jian，et al.Global time-energy optimal planning of industrial robot trajectories［J］.Journal of Mechanical Engineering，2010，46（9）：19- 25.

［12］杨玉维，赵新华，孙启湲，等.基于多体动力学特性的机械手时间最优轨迹规划［J］.机械工程学报，2014，50（7）：8- 14.

YANG Yu-wei，ZHAO Xin-hua，SUN Qi-yuan，et al.Trajectory optimization of manipulator for minimum working time based on multi-body dynamic characters［J］.Journal of Mechanical Engineering，2014，50（7）：8- 14.

［13］史也，梁斌，王学谦，等.基于量子粒子群优化算法的空间机器人非完整笛卡尔路径规划［J］.机械工程学报，2011，47（23）：65- 73.

SHI Ye，LIANG Bin，WANG Xue-qian，et al.Cartesian non-holonomic path planning of space robot based on quantum-behaved particle swarm optimization algorithm［J］.Journal of Mechanical Engineering，2011，47（23）：65- 73.

［14］GUO J C，WANG X J.Trajectory planning of redundant robot manipulators using QPSO algorithm［C］∥Proceedings of the 8th World Congress on Intelligent Control and Automation.Jinan：［s.n.］，2010：403- 408.

［15］张书涛，张震，钱晋武.基于Tau理论的机器人抓取运动仿生轨迹规划［J］.机械工程学报，2014，50（13）：42- 51.

ZHANG Shu-tao，ZHANG Zhen，QIAN Jin-wu.Bioinspired trajectory planning for robot catching movements based on the Tau theory［J］.Journal of Mechanical Engineering，2014，50（13）：42- 51.

［16］戈新生，孙鹏伟.自由漂浮空间机械臂非完整运动规划的粒子群优化算法［J］.机械工程学报，2007，43（4）：34- 38.

GE Xin-sheng，SUN Peng-wei.Particle swarm optimization algorithm of the non-holonomic motion planning for mechanical arm in free floating space［J］.Journal of Mechanical Engineering，2007，43（4）：34- 38.

［17］倪敬，邵斌，蒙臻，等.液压拉床双缸IPSO-PID伺服同步驱动控制研究［J］.中国机械工程，2013，24（11）：1494- 1500.

NI Jing，SHAO Bin，MENG Zhen，et al.IPSO-PID servo synchro control on hydraulic broaching machine with dual cylinder［J］.China Mechmical Engineering，2013，24（11）：1494- 1500.

［18］黄进，胡英，马孜，等.基于量子粒子群优化算法的工业机器人与外部轴标定［J］.机械工程学报，2009，45（7）：63- 67.

HUANG Jin，HU Ying，MA Zi，et al.Industrial robot and external axle calibration based on particle swarm optimization［J］.Journal of Mechanical Engineering，2009，45（7）：63- 67.

Trajectory planning algorithm for hydraulic servo manipulator of three freedom

LIU Xiang-qi1，2，MENG Zhen1，NI Jing2，ZHU Ze-fei2
（1.School of Mechanical Engineering and Automation，Zhejiang Sci-Tech University，Hangzhou 310018，China；2.School of Mechanical Engineering，Hangzhou Dianzi University，Hangzhou 310018，China）

A hydraulic manipulator trajectory planning algorithm based on non-axis driving space was proposed by introducing the closed chain vector kinematics model and the 5-order B-spline curve interpolation approximation theory.For the optimization problem of the total running time of the manipulator when met the kinematic constraints，the improved particle swarm optimization was introduced to optimize the solving step，so as to realize the time optimal continuous trajectory curve.The experimental results of practical application showed that the absolute error was less than 25 mm between the actual tool center point（TCP）trajectory and the desired trajectory.The research can solve the motion planning of the non-joint driving hydraulic manipulator and improve the efficiency of complex path planning algorithm.

closed-chain model；trajectory planning；B-splines；particle swarm optimization

10.3785／j.issn.1008-973X.2015.09.022

TP 241.2

A

1008- 973X（2015）09- 1776- 07

2014- 11- 03. 浙江大学学报（工学版）网址：www.journals.zju.edu.cn／eng

刘湘琪（1975－），女，博士生，从事机械设计及理论研究.ORCID：0000-0001-8782-566X.E-mail：lxiangqi＠hdu.edu.cn

朱泽飞，男，教授，博导.ORCID：0000-0002-6876-8257.E-mail：zzf.3691＠163.com