直行、左转车道占用所造成排队长度、事故持续时间、事故横断面实际通行能力间的关系
张丽娟等
【摘 要】本文就车道因交通事故被占用,导致道路横断面通行能力在单位时间内降低引起车辆排队,出现交通阻塞的问题进行统计分析,估算车道被占用对道路通行能力的影响程度,估算结果可为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设计路边停车位等提供重要理论依据。
【关键词】排队论;流波动理论;基本通行能力;实际通行能力;拥挤消散时间
0 引言
车道被占用对城市交通能力有着很大的影响,其中造成车道被占用的因素包括交通事故、路边停车、占道施工等,这些因素都会导致路段各车道通行能力有所下降。由于目前我国城市道路具有交通流密度大、连续性强等特点,往往一条车道被占用,就会影响该路段所有车道的通行能力,即使占用时间很短,也会引起车辆排队,造成交通堵塞。
通过本文分析,将为交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等提供理论依据。
1 问题分析
本文主要分析事故发生在直行和左转车道时,所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系。针对此问题我们运用排队论相关知识和车流波动理论结合交叉口信号控制的相关知识建立模型。首先讨论事故横断面实际通行能力、路段上游车流量与车辆排队长度的关系,然后绘制出车辆累计及消散过程图,讨论随着事故持续时间的变化,事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量三者间的关系。
2 问题的假设
1)所有的车都是匀速行驶的;
2)所有司机遵循交通规则;
3)各道路每天通过关口的流量都相等;
4)通往关口的所有车辆完全相同;
5)在进行实际通行能力计算时,该路段所有通过车辆均为标准车型,车身长度为6m;
6)在进行路段上游车流量计算时,选取1.2和2.0分别作为中型客车和大型客车的标准车型换算系数;
7)车辆到达服从泊松分布,服务服从负指数分布;
8)计算横断面实际通行能力的假设:
(1)修正系数为0.96;
(2)侧向净空修正系数为0.94;
(3)该路段纵坡小于7%,不予修正;
(4)不需要进行视距不足的修正;
(5)横向干扰修正时拥挤情况下修正系数为0.6,不拥挤情况下为0.75;
(6)驾驶员熟悉路况程度的修正系数为0.95;
(7)在事故发生后被占用的两车道无服务能力。
3 模型的建立
3.1 排队论模型
3.2 车流波动理论模型
传统的排队论理论单纯使用需求量和通行能力推算排队长度,由于未考虑车流波动的影响,从而使估算结果与实际出入很大。现用车流波动理论分析发生交通事故后路段上车辆排队的形成和消散过程,推导出估算排队长度与消散时间的公式[3]。
车流波动:假设上游交通需求量大于事发路段现有通行能力,到达车流在事故地点陆续减慢速度甚至停车而集结成密度较高的队列,事故解除后,由于路段畅通,通行能力恢复,排队车辆又陆续加速而疏散成一列具有适当密度的车队,车流中两种不同密度部分的分界面经过一辆辆车向车队后部传播的现象。当车流密度由低密度向高密度转变时,所体现的车流波为集结波[1-3]。
4 算例
4.1 数据处理
根据某240米长三车道路段发生的占用直行、左转车道的真实事故经过简化,代入数据,在求解过程中,将事故横断面实际通行能力看做该段道路的服务率(μ),路段上游车流量作为该段道路的平均到车率(λ)。
4.2 问题分析求解
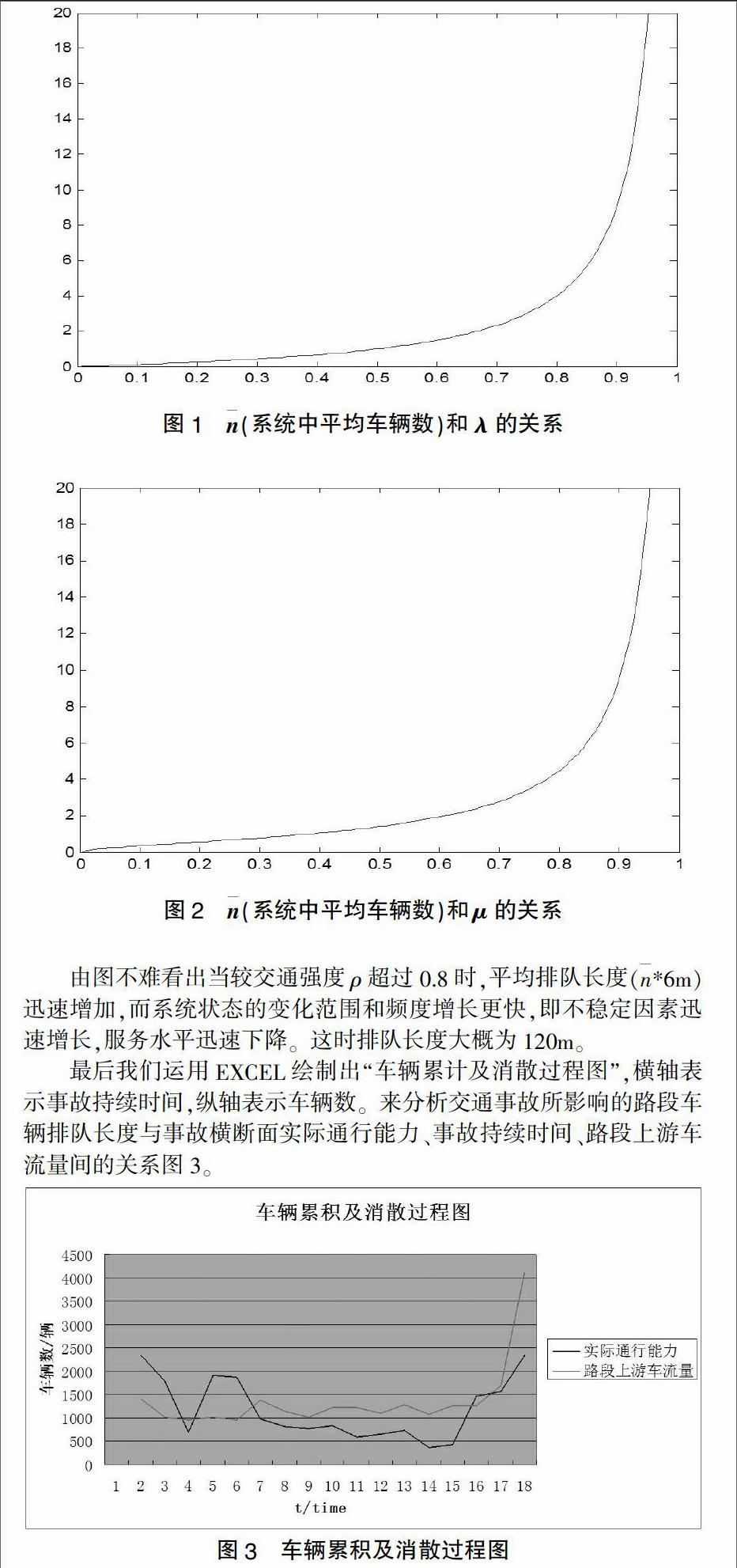
最后我们运用EXCEL绘制出“车辆累计及消散过程图”,横轴表示事故持续时间,纵轴表示车辆数。来分析交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系图3。
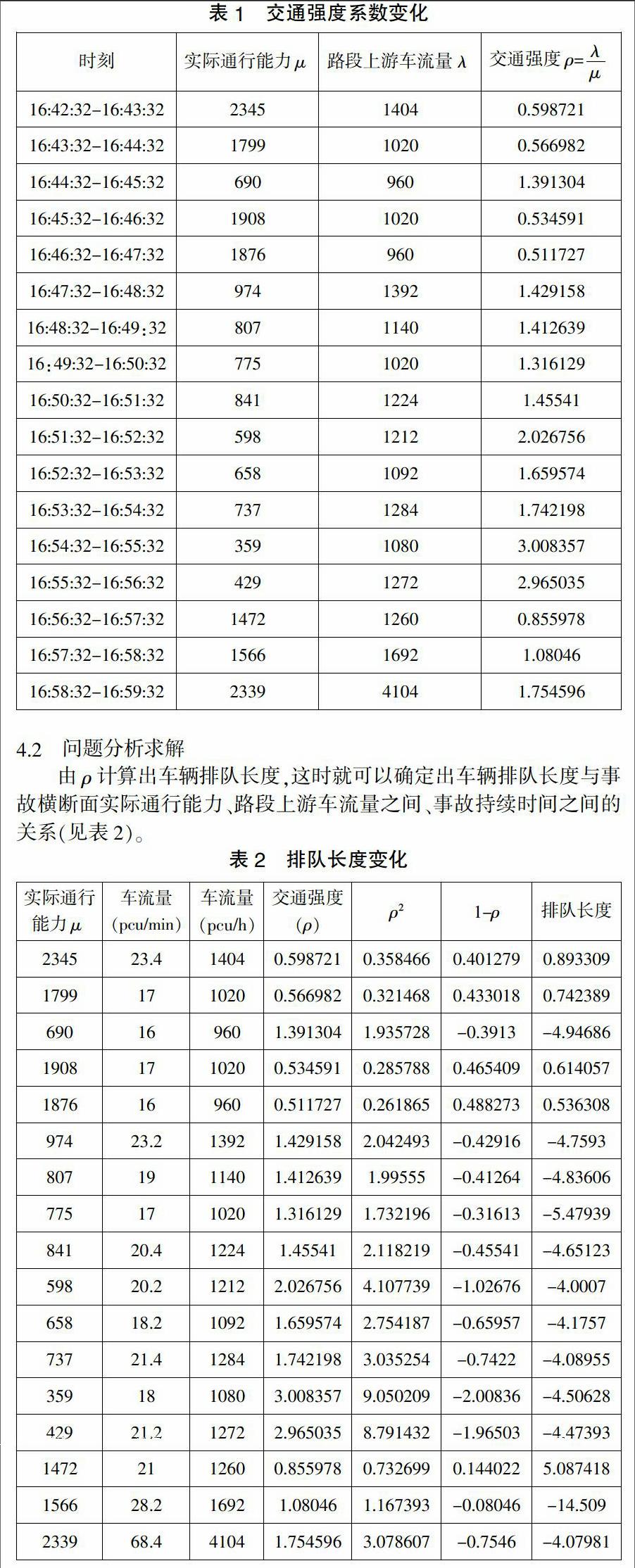
分析上图可知,在事故发生后的前3分钟,实际通行能力μ大于路段上游车流量λ,系统稳定,ρ<1,车辆排队长度大约为6m;从事故发生后的第3分钟开始到事故发生后第13分钟这段时间,实际通行能力μ小于路段上游车流量λ,系统不稳定,ρ<1,排队长度迅速增加,大约排队长度为120m;从事故发生后的第14分钟开始,事故撤离,拥堵情况得到缓解,实际通行能力增强,路段车辆恢复正常行驶。
5 结论
在城市道路具有交通流密度日益增大大、连续性强、新手驾驶增多等特点的今天,车道被占用的情况种类繁多、复杂,本模型的建立可正确估算车道被占用对城市道路通行能力的影响程度,对交通管理部门正确引导车辆行驶、审批占道施工、设计道路渠化方案、设置路边停车位和设置非港湾式公交车站等有重要意义。
针对该模型出现的拥挤情况,我们可以采取一定的措施进行车流的疏散,比如在距事故发生横断面一定距离处设置警示标志,告知上游到达车辆前方发生交通事故,以便驾驶员提早选择插车时机汇入优先车道。这样可减少拥挤持续时间和系统中的排队车辆数。
【参考文献】
[1]徐吉谦,陈学武.交通工程总论[M].北京:人民交通出版社,2012,11.
[2]张伯生,张丽.运筹学[M].北京:科学出版社,2012,6.
[3]孔惠惠,秦超,李新波,李引珍.交通事故引起的排队长度和消散时间的估算[J]. 铁道运输与经济,2005,27(5).
[4]马健霄,吕志英,王大明.城市道路交通能力分析和改善技术[J].南京林业大学学报:自然科学版,2001.25(2).
[5]龚曙明.应用统计学[M].北京:清华大学出版社,2005,8.
[责任编辑:杨玉洁]

