德州市地下水运动数值模拟研究

王希科等

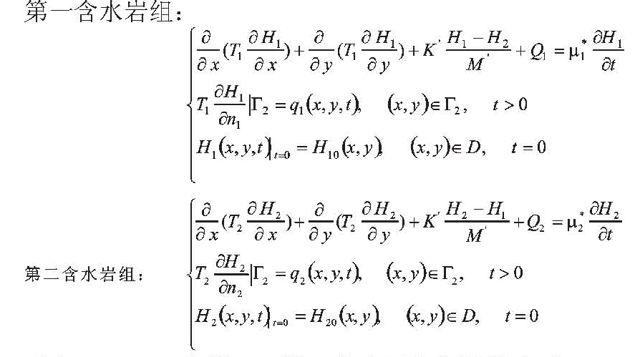
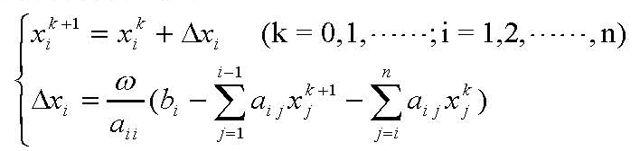
摘 要：根据德州市区水文地质条件，将含水层概化为非均质、有越流向的二维承压水流模型，根据水量均衡原理建立三角网格剖分节点的差分方程，采用逐次超松弛迭代方法解系数矩阵；根据实测资料对模型进行识别与调试，采用识别后的有关数据，进行地下水量均衡计算和资源量计算，发现补给量小于排泄量，年超采量为393万m3/年，对未来地下水动态进行了预测，不同条件下地下水位降深达5.6～61.3m。研究发现随着超采时间的延长及超采量的加大，地下水位将持续下降，地下水漏斗面积不断扩大，导致地面沉降、水质恶化等环境地质问题进一步恶化。为防止地下水超采引起的环境地质问题进一步恶化，提出了科学的防治措施及建议。

关键词：地下水运动；数值模拟；地下水漏斗；地面沉降；环境地质问题

1 数学模型

近年来，德州市地下水开采量大于补给量，地下水位处于持续下降状态。根据深层水水资源概念，不仅将补给资源全部开采了出来，还利用了一部分储存资源。本文在充分研究德州市水文地质条件的基础上进行了模型概化与计算。

1.1 数学模型的建立

根据研究区水文地质条件，将主要开采含水层分为两个含水岩组，上部称为第一含水层（埋深300～500米以上），下部称为第二含水层（埋深500～800米），中间为一越流层（见图1）。第一、第二含水岩组均可概化为非均质、有越流项的二维承压水流模型，数学模型如下：

式中：H1、H2为第一、第二含水层水位标高（m）；H10、H20为第一、第二含水层初始水位标高（m）；T1、T2为第一、第二含水层导水系数（m2/d）；μ1*、μ2*为第一、第二含水层贮水系数（无量纲）；K 为弱透水层渗透系数（m/d）；M 为弱透水层渗透系数（m/d）；B= K/ M为越流系数（无量纲）；Γ2为渗流区域上的第二类边界；q1、q2为第一、第二含水层为第二类边界上的单宽流量（m3/d·m）；n1、n2为第一、第二含水层为第二类边界某点的外法线方向；Q1、Q2为第一、第二含水层汇源项（m/d）；x、y为平面坐标（m）；t为时间（d）；D为渗流区域（m2）。

1.2 数值解法

数学模型第一式的物理意义为：在区域面积和时刻均趋于无限小时含水层中地下水的均衡方程。基本方程左侧的第一、二项表示侧向流入和流出含水层流量的差值（单位时间单位面积含水层而言）；第三项为越流项；第四项为源汇项，表示单位面积含水层上垂向补给或排泄流量；右侧表示单位时间、单位面积含水层贮水量的变化率。若面积和时段不取无限小而采用有限值，则可以用近似方法逼近方程各项的极限值，根据水量均衡原理可建立三角网格剖分节点的差分方程。节点i的差分方程如下：

第一含水岩组：

第二含水岩组：

式中：Cij为侧向水量的水位系数；H1、H2为第一、第二含水层水位标高；B 为越流系数；Q1（i）、Q2（i）为第一、第二含水层垂向水量；Fi为贮存量的水位系数；j为节点i周围的节点号（i，j=1， …n，节点个数）；t为时间步长；k为计算时刻（k =1， …m，时段数）。

若用X表示未知数的列向量： ；用A表示方程组的系数矩阵，b表示常数项列阵，则上述数值方程组可写为矩阵形式：AX=b。

用水量均衡原理推导出的不规则网格有限差分方程，其系数矩阵A是一个具有对角线优势的高度稀疏的对称正定矩阵，对于大型稀疏矩阵（A的阶数n较大，但零元素较多），利用迭代法求解是较合适的。由逐次超松弛迭代方法SOR（Successive Over Relaxation Method）收敛的判别定理知：如果A为对称正定矩阵且0<ω<2，则解AX=b的SOR方法收敛。因此，本文选择SOR方法，它是高斯—塞德尔迭代方法的一种加速方法，是解大型稀疏矩阵方程组的有效方法之一，它具有计算公式简单，程序设计容易，占用计算机内存少等优点。下面对其迭代公式作一简述。

现状开采量条件下，随开采时间的增加，地下水水位降深愈来愈大，t=10年時，第一含水层水位降深s为15.06～33.66m，第二含水层水位降深s为22.38～31.32m；第二含水层开采量增加20%条件下，相同时间与节点的降深大于现状开采量下的降深，t=10年时，第一含水层水位降深s为17.75～36.62m，第二含水层水位降深s为23.12～36.24m。

3结论

①根据德州市区地下水运动数值模拟，发现现状地下水年超采量为393万m3/年，连年超采已引起区域地下水位降落漏斗，并已引起地面沉降、水质恶化等一系列的环境地质问题，如1991年至2006（15年）德州市累计地面沉降总量为710.5mm，年均沉降量为47.4mm/a，沉降中心累计沉降量为992mm，沉降范围已与周边的河北省衡水、沧州地面沉降连为一片。

②为防止地下水超采引起的环境地质条件进一步恶化，建议总体规划、合理利用水资源，施行最严格的水资源管理制度，建立地下水环境监测网络，建立有效的节水措施及地下水保护措施，实现水资源的可持续利用。

参考文献

[1] 陈崇希，唐仲华.地下水流动问题数值方法[M].中国地质大学出版社.2002.

[2] 孙讷正.地下水流的数学模型和数值方法[M].地质出版社.1981.

[3] 朱学愚，钱孝星，刘新仁.地下水资源评价[M].南京大学出版社.1987.

[4] 李庆扬，王能超，易大义.数值分析[M].华中科技大学出版社.2005.

[5] 薛禹群.地下水动力学[M].地质出版社.1986.

[6] 张蔚榛.地下水非稳定流计算和地下水资源评价[M].科学出版社.1983.

[7] 德州市水文地质调查研究报告[R].德州市水文地质勘察院.2006.

[8] 陆金甫，关治.偏微分方程数值解法[M].清华大学出版社.1987.

[9] 王大纯，张权，史毅虹等.水文地质学基础[M].地质出版社.1994.

[10] 蔡文晓.德州市深层地下水开采与地面沉降关系研究[D].吉林大学.2009.

[11] 张缨，周家权，任绪伟.德州市地下水漏斗引发生态问题及应对措施[C].

[12] 赵全升，冯娟，安乐生.德州市深层地下水水质演化研究[J].地理科学，2009，29（5）.

[13] 冯娟.德州市深层地下水动态变化与模拟研究[D].青岛大学.2008.

[14] 卢文喜.地下水运动数值模拟过程中边界条件问题探讨[J].水利学报，2003，（3）.

[15] 王元行，王吉良，王华敏.华北地区沧县出现的地下水环境问题与对策[J].水资源保护，2003，（4）.