大气中PM2.5浓度的空间表征方法研究
刘妍月 李军成

摘要:针对大气中PM2.5浓度的空间表征问题,提出了一种基于距离反比加权法的克里金插值模型进行PM2.5浓度空间表征的方法。该方法根据各浓度监测站点公布的PM2.5浓度实时数据以及谷歌地球、百度地图中的地理信息,建立能够表征整个城市PM2.5浓度的空间连续曲面,从而获得整个城市各个角落的PM2.5污染情况。实例表明,基于距离反比加权法的克里金插值模型是一种有效的PM2.5浓度空间表征方法,从而为大气中PM2.5污染的防控提供一定的决策依据。
关键词:
PM2.5浓度;空间表征;克里金插值;距离反比加权法
DOI: 10.14068/j.ceia.2015.06.019
中图分类号:X513文献标识码:A文章编号:2095-6444(2015)05-0084-05
PM2.5虽然在大气成分中含量很少,但对空气质量和能见度等有重要的影响,因此已成为我国环境污染防控最重要的对象之一[12]。2013年1月14日,亚洲开发银行和清华大学发布的一份名为《迈向环境可持续的未来:中华人民共和国国家环境分析》[3]中指出,世界上污染最严重的10个城市之中有7个城市位于中国,中国500个大型城市中,只有不到1%达到世界卫生组织空气质量标准。可见,中国的环境污染已经到了相当严重的地步。
近年来,针对大气中PM2.5浓度的空间表征问题,国内外学者先后采用了反距离权重插值、多项式插值、克里金插值等传统空间插值方法进行城市PM2.5浓度的空间表征研究[45]。为了进一步提高精度,Liao等人[6]运用3种克里金插值方法对PM2.5浓度进行了空间表征并对其模型精度进行了评价;Wu等[7]使用反距离权重插值、克里金插值和协同克里金插值等3种方法研究美国南加州森林大火前后空气中的PM2.5浓度变化,结果显示火灾之前反距离权重插值方法预测效果较克里格插值方法好;王敏等[8]在肯定BP人工神经网络预测模型可用于揭示PM2.5浓度空间变异特征的同时,也证实了其相对于普通克里格插值方法在固定空间点位准确预测PM2.5浓度方面的优势。
目前国际上普遍采用大气环境定点监测的方式来获取各城市的污染状况,而各监测点观测结果只可以表征监测点周边一定半径范围内的浓度情况,无法表征整个城市的污染状况及其空间差异,因此,如何基于离散监测站点的监测浓度数据准确地获取整个城市污染连续空间曲面也成为一个亟待解决的关键问题。为此,本文试图以普通克里金插值模型为基础,结合距离反比加权法来进一步优化插值模型,提出一种基于距离反比加权法的克里金插值模型进行PM2.5浓度空间表征的方法,为解决基于稀疏监测数据准确来获取城市PM2.5污染空间分布规律这一问题提供一种有效的方法。
1模型的建立
基于距离反比加权法的克里金插值模型进行PM2.5浓度的空间表征研究的基本流程如图1所示。
1.1数据采集
建立PM2.5浓度空间曲面之前需要收集某地区各监测站点的地理位置数据以及各站点公布的PM2.5浓度数据。本文采用的PM2.5浓度观测数据来源于政府环境保护部门网站公布的PM2.5浓度实时数据。为了确保普通克里金插值方法预测PM2.5浓度的精度及后续精度评价工作的开展,数据将选用多组不同日期不同时刻的PM2.5浓度数据。地理信息数据是以经纬度坐标为基础的特殊数据。在利用经纬度計算距离时,两点之间的过球心大圆距离最接近实际距离,所以在计算时使用的是球面距离,计算公式为:
d=2Rarcsinsin2△φ2+cosφscosφfsin2△λ2(1)
式中,φs、φf代表两点的纬度;△φ和△λ分别代表纬度和经度之间的差值;R为地球半径。
在克里金插值模型中,考虑到计算的复杂性,本文是直接将纬度、经度对应直角坐标的X轴,Y轴,假定每度经度和纬度之间的距离都看成是相等的。直接用坐标点之间的欧式距离代表现实中两地的距离。每度代表的距离为111.32 km。这也相当于使用了地图投影中的圆柱投影。谷歌地球和百度地图使用的就是圆柱投影。
1.2建立普通克里金插值模型
克里金(Kriging)方法[911]又称空间局部插值法,是一种以变异函数理论和结构分析为基础,在有限区域内对区域化变量进行无偏最优估计的一种方法。空间数据通常是一系列采样观测值,分布往往很不规则,但用户在某些情况下需要获知相同区域内未知观测点的数据,根据空间相关性原则,这些未知点与采样点之间存在着空间上的相关性,通常情况下,距离越近的点,其特征值越相似,反之亦然,因此空间插值算法应运而生,是通过已知点推求未知点的计算方法[1213]。克里金插值的核心所示变异函数,其定义为[11]:
[HJ0][QH0][HT5”SS]环境影响评价第37卷[HT][KH-*8D][HJ]
[HJ0][QH0]第6期
刘妍月等:大气中PM2.5浓度的空间表征方法研究
[HT][KH-*8D][HJ]
γh=12Nh∑Nhi=1Zμa-Zμa+h(2)
式中,Nh为距离相隔h的点对数;Z是特征值;γh表示变异函数值。
由式(2)可知变异函数的核心思想是按照点对间的距离大小分组,对每一个组中的每一个点对进行插值计算,求算平均值,即可得到变异函数值。在普通克里金插值模型中,待测点的特征值是根据周围的已知点的线性组合推求得出,可表示为:
Z*x=∑ni=1λiZxi(3)
式中,Z*x表示待测点x的估计值;Zxi表示x周围观测点xi的特征值;n为参与计算的观测点的个数;λi为权重系数,表示各空间样本点处的观测值对估计值Zxi的贡献程度,区域化变量Zx的数学期望E=Zx=m可以是已知的或未知的。因此,克里金插值方法可以简单地表达为:
Zs=μs+s(4)
式中,s为不同位置的点,本文为经纬度表示的坐标;Zs为s处的变量值,它可以分解为确定趋势值μs和自然相关随机误差εs。
1.3基于距离反比加权法的克里金插值
距离反比加权法[14]可表示为:
Zx0=∑ni=1Zxiγxi,x0∑ni=11γxi,x0(5)
式中,Zxi为xi处的平稳过程值;γxi,x0为x0与xi之间的变异函数值,用两点之间的距离代替。
1.4获取PM2.5浓度的空间曲面
获取PM2.5浓度的空间曲面时,首先将整个区域划分为网络,以某一顶点的浓度估计值代替整个网络区域的PM2.5浓度值,根据关注区域内已知点的坐标及其浓度值,采用距离对数反比加权法计算已知点对未知点浓度值的影响因素,在此基础上计算未知点的PM2.5浓度值。
2应用实例
本文选取的研究范围为湖南省长沙市,位于东经111°53′~114°15′,北纬27°51′~28°41′,包括岳麓区、天心区、雨花区、望城区等长沙市区,虽然未覆盖长沙市全部地区,但人口密度非常大。长沙市的面积为11819.5平方公里,但仅有10个PM2.5浓度监测点,具体分布如图2所示。
注:图片来源于长沙市环境保护局网站。
图2长沙市PM2.5浓度监测站点分布
Fig.2Monitoring sites of PM2.5 concentration in Changsha city
依据PM2.5浓度以及污染指数可以大致将污染等级分为六级,如表1所示。
2.1长沙市PM2.5浓度数据与地理信息采集
本文采用的PM2.5浓度观测数据来源于长沙市环境保护局网站公布的10个监测点数据,分别收集了2015年2月23日11:00时、2015年2月24日18:00时以及2015年2月25日15:00时三个不同日期不同时段的PM2.5浓度数据,并从谷歌地球和百度地图中逐个收集长沙市10个监测站点的经纬度,PM2.5浓度与座标数据如表2所示。
2.2长沙市PM2.5浓度空间曲面的建立
2.2.1绘制监测站点位置散点图
利用采集的10个PM2.5浓度监测站点的经纬度数据可以绘制出其位置散点图,如图3所示。
2.2.2绘制PM2.5浓度空间曲面
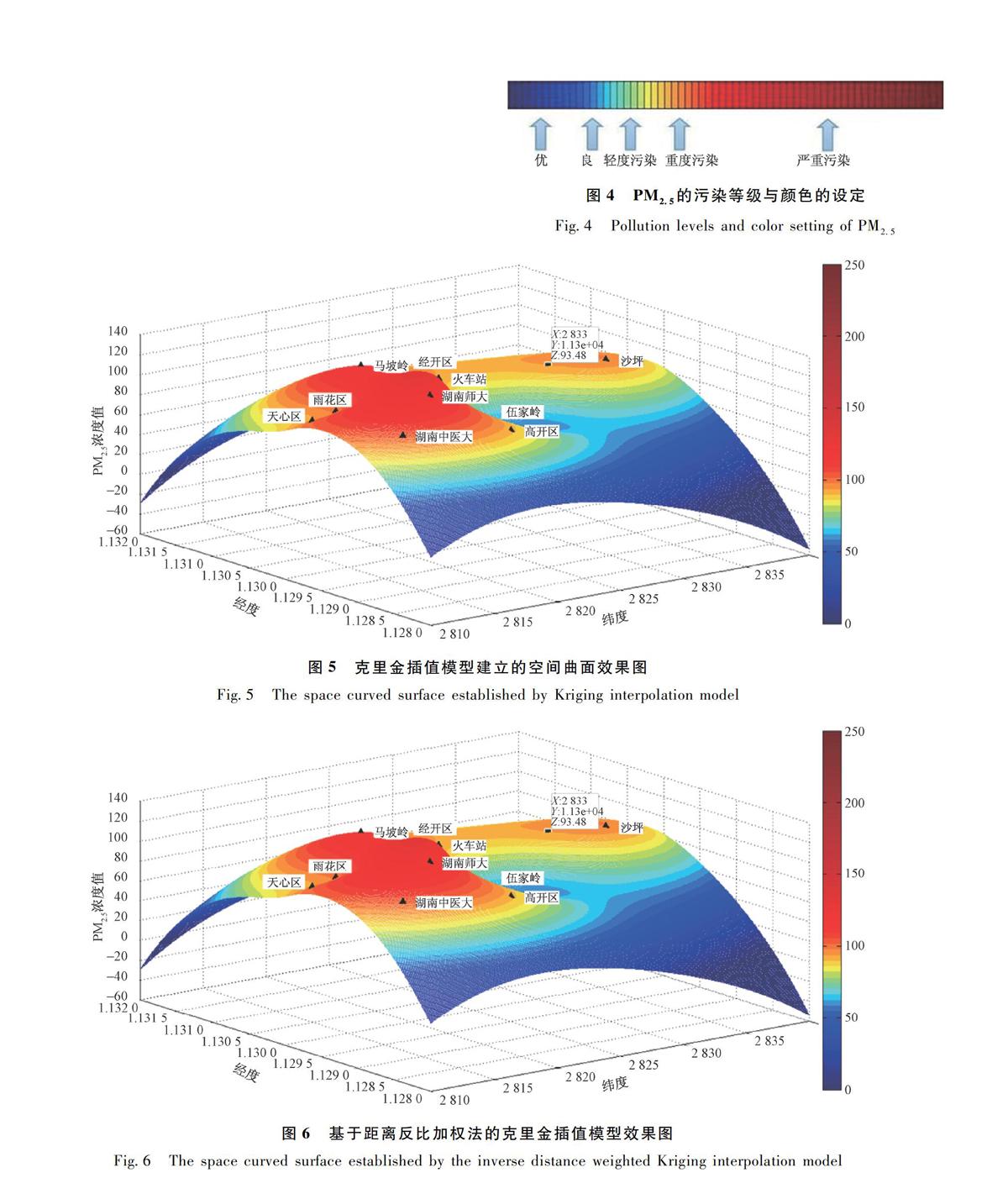
利用采集的某时刻的PM2.5浓度实时数据结合克里金插值模型建立PM2.5浓度空间分布曲面,选取的数据为长沙市2015年2月23日11:00时的PM2.5实时浓度数据,曲面上的每一个点都有一个(X, Y, Z),X, Y分别表示此点的纬度和经度,Z表示此点的PM2.5浓度值,可以通过点击鼠标在任意位置查看,如图4所示;图5为克里金插值模型建立的空间曲面效果图;图6为基于距离反比加权法的克里金插值模型效果图。
2.3误差分析
假设研究变量为Z(x),依次删去Z(x)在采样点xi(i=1,2,…,N)处的属性值Z(xi)(i=1,2,…,N),其他点的属性值保持不变,利用剩下的N-1个点的属性值,插值被删除的采样点上的属性值Z*(xi),并对N个插值计算结果与实际的结果进行比较,进行误差的统计学分析,具体误差分析方案如下:
方案1:根据2015年2月23日11:00时的浓度数据,去掉湖南中医药大学站点的浓度数据,实际浓度为102 μm/m3。
方案2:根据2015年2月23日11:00时的浓度数据,去掉伍家岭站点的浓度数据,实际浓度为73 μm/m3。
方案3:数据改为2015年2月24日18:00时浓度数据,去掉火车站点的浓度数据,实际浓度为126 μm/m3。
方案4:数据改为2015年2月24日18:00时浓度数据,去掉沙坪点的浓度数据,实际浓度为93 μm/m3。
方案5:数据改为2015年2月25日15:00时浓度数据,去掉高开区点的浓度数据,实际浓度为110 μm/m3。
方案6:数据改为2015年2月24日15:00时浓度数据,去掉经开区点的浓度数据,实际浓度为107 μm/m3。
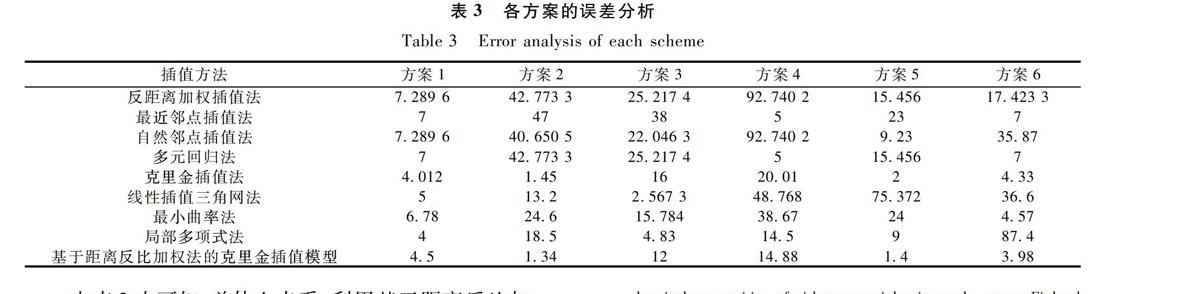
用PM2.5浓度数据对各种插值方法进行交叉验证,其结果见表3。
由表3中可知,总体上来看,利用基于距离反比加权法的克里金插值模型进一步提高了插值精度。但是也要注意到,该模型在某些情况下仍存在相对较大的误差,这是因为监测站点的实时监测数据本身存在一定的误差,另外还存在着诸多影响PM2.5浓度的因素,如机动车尾气、施工扬尘、火电厂分布等,这些因素都对PM2.5浓度数据存在一定的影响。适当地考虑这些因素对PM2.5浓度的影响可逐渐提高插值模型的精度。
3结语
本文提出了一种基于距离反比加权法的克里金插值模型进行PM2.5浓度空间表征的方法。该方法能在稀疏监测数据输入条件下获得城市内部PM2.5污染的空间分布规律。通过与其他一些方法进行比较发现,本文提出的方法是一种有效的PM2.5浓度空间表征方法,从而为环境保护部门的工作、人们日常的生活出行提供了一定的参考依据。
参考文献(References):
[1]邵龙义, 时宗波, 黄勤. 都市大气环境中可吸入颗粒物的研究[J]. 环境保护, 2000, 1: 2429.
[2]Makkonen U, Hellen H, Anttila P, et al. Size distribution and chemical composition of airborne particles in southeastern Finland during different seasons and wildfire episodes in 2006[J]. Science of the Total Environment, 2010, 408(3): 644651.
[3]张庆丰. 迈向环境可持续的未来:中华人民共和国国家环境分析[M]. 北京: 中國财政经济出版社, 2012.
[4]Jerrett M, Burnett R T, Ma R J, et al. Spatial analysis of air pollutionn and mortality in Los Angeles[J]. Epidemiology, 2005, 16(6): 727736.
[5]Bayraktar H, Turalioglu F S. A kringing based approach for locating a sampling site in the assessment of air quality [J]. Stochastic Environmental Research and Risk Assessment, 2005, 19(4): 301305.
[6]Liao D, Peuquet D J, Duan Y, et al. GIS approaches for the estimation of residentiallevel ambient PM concentrations [J]. Environmental Health Perspectives, 2006, 114(9): 13741380.
[7]Wu J, Winer A M, Delfino R J. Exposure assessment of particulate matter air pollution before, during, and after the 2003 Southern California wildfires [J]. Atmospheric Environment, 2006, 40(18): 33333348.
[8]王敏, 邹滨, 郭宇, 等. 基于BP人工神经网络的城市PM2.5浓度空间预测[J]. 环境污染与防治, 2013, 35(9): 6366.
[9]孙洪泉. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社, 1990.

