多间隙高重合度齿轮传动系统动力学分岔与稳定性分析*

李发家 朱如鹏 靳广虎 鲍和云 叶福民

(南京航空航天大学 机电学院，江苏 南京210016 )

高重合度(HCR，重合度＞2)直齿圆柱齿轮传动同时啮合的轮齿对数较多，单对轮齿承受的载荷小，啮合刚度变化幅值较小，传动系统具有承载能力大、传动平稳等优点，因此高重合度齿轮传动备受关注.

许多学者对齿轮传动的动力学特性进行了研究.Tuplin［1］最先提出采用集中质量法计算齿轮动态载荷系数，采用齿轮的冲击解释齿轮的动态激励，开创了齿轮研究的新思路.Retting［2］对HCR 齿轮的噪声与普通重合度(NCR)齿轮的噪声进行了试验对比，结果表明HCR 齿轮的噪声要低于NCR 齿轮.Harris［3］采用试验方法得到齿轮的刚度，提出采用提高重合度的方法来减小刚度的波动，并对轮齿的动载荷进行了求解;Ozguven 等［4］分析了时变啮合刚度的单自由度齿轮传动系统的扭振响应;Benton［5］采用相平面法对齿轮的稳态响应和共振稳定性进行了分析;Kahraman 等［6-9］分析了含轴承径向支承和齿侧间隙的三自由度直齿轮传动系统的非线性动力学特性，建立了齿轮系统分析模型，但该模型仅考虑了沿啮合线方向的支承.Liou 等［10］采用拉格朗日法建立了考虑输入、输出轴扭转位移的四自由度齿轮动力学模型.

许多学者采用有限元法对高重合齿轮的弯曲应力和载荷分配进行了计算和研究［11-12］. 渠珍珍等［13-14］对高重合度齿轮的实现方法和动态特性进行了研究，分析了高重合度行星齿轮传动系统的动态特性;方宗德等［15］对高重合度齿轮的载荷分配、刚度计算、动态特性和优化设计进行了计算和研究;王三民等［16］研究了高重合度齿轮的动力学特性，并提出了齿轮齿廓修形的方法;刘梦军［17］建立了含齿侧间隙的单对齿轮副非线性动力学模型，利用模型的分段线性特点对模型的动态特性进行了研究.

由文献可知，国内外学者对单对齿轮传动系统的动态特性进行了大量研究，但针对多间隙的高重合度齿轮传动系统的动力学分岔和稳定性研究较少.当齿轮系统运动状态处于混沌运动、跳跃和分岔状态时，会对系统的噪声、运行平稳性和可靠性造成严重的影响，严重时会直接导致齿轮系统的破坏.因此，有必要对HCR 齿轮的分岔、跳跃、混沌等动力学特性进行深入研究，这对保证HCR 齿轮传动的高可靠性、高承载性能等优点具有重要意义.

文中对HCR 齿轮传动系统的啮合刚度进行计算，采用能量法建立了考虑轴承间隙、齿侧间隙和时变啮合刚度的齿轮传动系统的6 自由度动力学模型，研究间隙高重合度齿轮传动系统的分岔和跳跃特性，以期为高重合度齿轮传动系统的设计提供理论支撑.

1 多间隙、时变刚度齿轮传动系统的动力学模型

图1 为考虑轴承径向支承间隙和齿侧间隙的齿轮传动系统动力学模型.

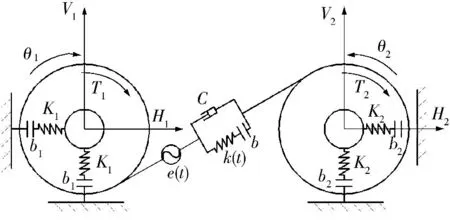
图1 多间隙齿轮传动系统动力学模型Fig.1 Dynamic model of gear transmission system with multiple clearances

图1 中，T1和T2分别为输入和输出扭矩;θ1和θ2为两齿轮的转动自由度;K1和K2分别为齿轮Z1和Z2的支承刚度;k(t)为啮合齿轮副的时变啮合刚度;C 为啮合齿轮副的啮合阻尼;e(t)为传动误差;b1和b2为轴承支承间隙的一半;b 为齿侧间隙的一半.

该系统共有6个自由度，其广义坐标X 可表示为

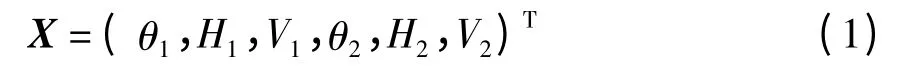
式中，V1和V2分别为齿轮Z1和Z2的纵向位移，H1和H2分别为齿轮Z1和Z2的横向位移.

2 高重合度齿轮的啮合刚度、啮合力和阻尼力

2.1 高重合度齿轮时变啮合刚度

齿轮重合度是表征同时啮合轮齿对数变化状态的参数，重合度对刚度的变化幅值具有较大影响［18］.文中采用改变齿顶高系数方式实现齿轮的高重合度，其齿轮参数如表1 所示，外啮合齿轮副的重合度为2.1.

表1 高重合度齿轮的基本参数及重合度Table 1 Basic parameters and contact ratio of HCR gear system

建立表1 参数所示的齿轮副有限元模型，对其刚度进行计算，齿轮平均刚度km=3.85 ×108N/m.采用六阶Fourier 级数对综合啮合刚度进行傅里叶变换，得到齿轮啮合刚度拟合曲线，如图2 所示.

图2 HCR 齿轮啮合刚度Fig.2 Meshing stiffness of HCR gear

拟合刚度的各次谐波参数Aki如表2 所示. 其中，Aki，sin为傅里叶拟合方程中各阶正弦项的系数，Aki，cos为傅里叶拟合方程中各阶余弦项的系数.

表2 各次谐波参数表Table 2 Coefficients of each harmonic

2.2 啮合力和阻尼力

啮合齿轮间的啮合力由啮合线上的相对位移和啮合刚度确定.啮合线上的相对位移由3 部分位移沿啮合线投影的等效位移组成，即各种误差的等效位移、齿轮中心横向与纵向位移的等效位移、齿轮啮合线上的相对转动等效位移［19］.

由误差引起的在啮合线上的等效位移e(t)为

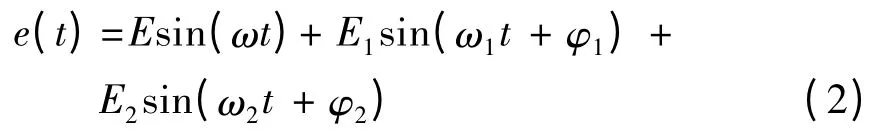
式中:E 为齿频误差;E1和E2分别为齿轮Z1和Z2的安装误差;φ1和φ2分别为齿轮Z1和Z2安装误差的初相位;ω1和ω2分别为齿轮Z1和Z2的转动角速度.

齿轮转动引起的齿轮副啮合线方向的相对位移Xr为

式中:rb1和rb2分别为齿轮Z1和Z2的基圆半径;α 为实际啮合角.则齿轮副的啮合力P(t)为

间隙函数f(Xn，bi)为

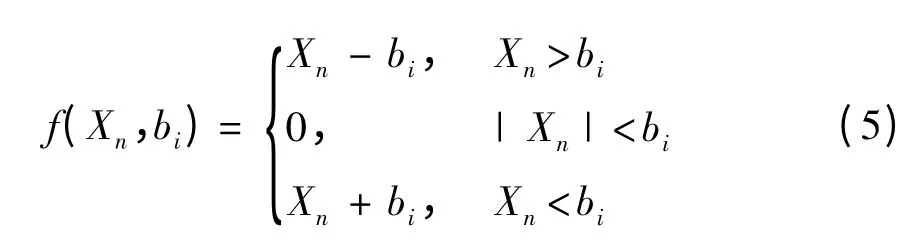
式中:Xn为间隙变量;Xn=Xr，H1，H2，V1，V2;bi为间隙;bi=b，b1，b2.

齿轮副的啮合阻尼力D(t)为

3 齿轮传动系统的动力学微分方程

根据图1 所示的传动系统动力学模型来分析齿轮Z1和Z2的能量变化，则由齿轮传动系统各方向上的能量守恒定律得到传动系统能量方程:

式中:M1和M2分别为齿轮Z1和Z2的质量.

设x1和x2分别为齿轮Z1和Z2的转动自由度θ1和θ2沿啮合线方向的当量位移，x1= θ1rb1，x2=θ2rb2.根据式(7)-(12)，对变量θ1、H1、V1、H2、V2、θ2求导并化简，可得整个系统的能量变化率［18］，如式(13)所示:

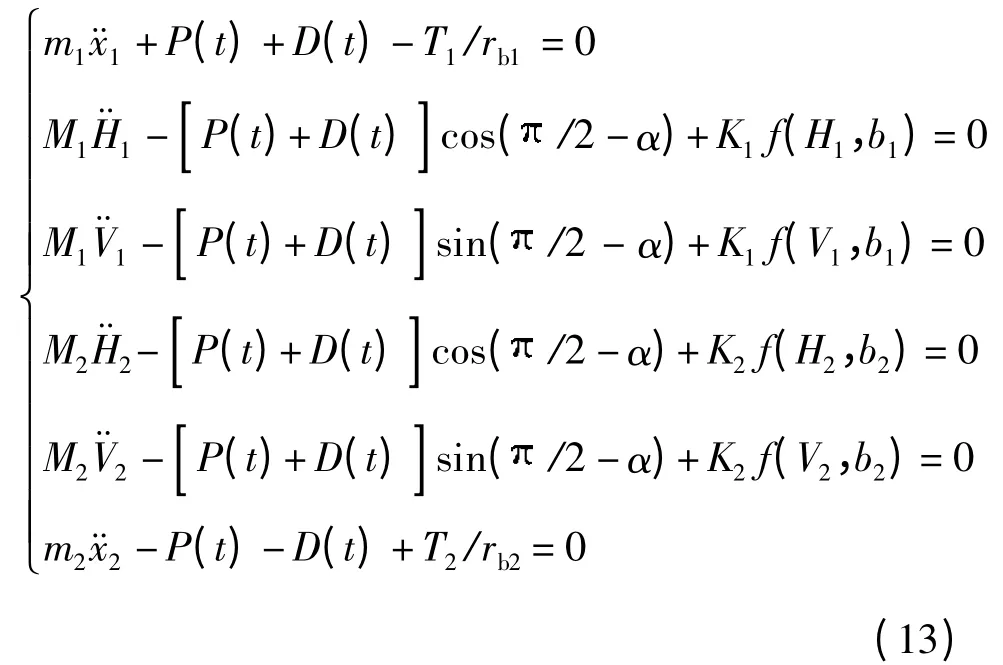
4 齿轮传动系统的分岔特性分析

多间隙高重合度齿轮传动系统的齿轮参数如表1所示，其余参数为:输入功率200 kW，齿侧间隙b=40 μm，齿频误差E =5 μm，偏心误差E1=E2=10 μm，支撑间隙一半b1=b2=10μm，支承刚度K1=2.0 ×108N/m，支承刚度K2=3.5 ×108N/m，位移标称尺度bc=10 μm，阻尼比ζ =0.043.采用变步长4 阶Runge-Kutta 求解无量纲方程(14)- (19)，并对计算结果进行处理，获得了不同参数对多间隙高重合度齿轮传动系统分岔特性的影响.

4.1 转速对传动系统分岔特性的影响

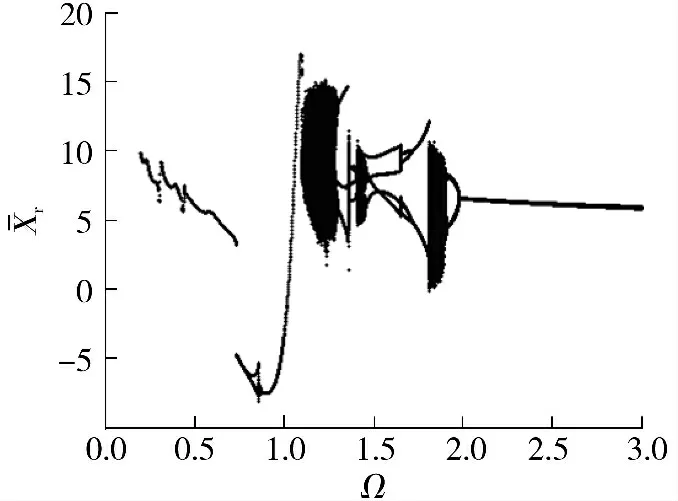
图3 系统随转速变化的全局分岔图Fig.3 Global bifurcation of system changing with speed

图4 平衡点分岔Poincaré 图Fig.4 Poincaré map at equilibrium piont

无量纲转速Ω 为1.1 ～2.0 时，系统具有丰富的分岔特性，其典型的Poincaré 图如图5 所示.当无量纲转速Ω 为1.1 时，系统由单周期运动突然跳跃进入混沌运动，呈现典型的激变特征. 在共振区域，高重合度齿轮通过激变途径进入混沌，这与其他齿轮传动系统具有相似的特点［20］.

图5 转速Ω 为1.0 ～2.0 时系统Poincaré 截面Fig.5 Poincaré map when Ω= 1.0 ～2.0

由于激变途径进入混沌多发生于含间隙系统［16］，因此在共振区域，间隙对高重合度齿轮的运行状态有较大影响. 当无量纲转速Ω 增大至1.29时，系统由混沌状态进入多周期运动状态;当无量纲转速Ω 增大至1.31 时，系统进入3 周期运动，无量纲转速Ω 继续增大，系统再次进入了混沌运动状态;在Ω 为1.46 时，系统跳出混沌运动状态进入4周期运动;当Ω 为1.61 时，系统短暂进入两周期运动，随之重复进入4 周期运动;当Ω 增大至1.72 时，系统进入两周期运动，随着无量纲转速的增加，系统又由两周期运动进入混沌运行状态;当Ω 为1.92时，系统激变进入稳定的两周期运动;在Ω 为1.98以后系统为稳定的单周期运动.

齿轮传动系统处于混沌运行区域，微小的波动会造成齿轮传动系统运行轨道的剧烈跳跃，其运行平稳性差，对系统的振动和寿命造成不利影响，因此设计齿轮时，系统的运动转速应尽量避开混沌运动区域的位置，使齿轮传动系统处于周期运行区域.

4.2 齿侧间隙对传动系统分岔特性的影响

根据图3 所示的高重合度齿轮传动系统啮合线位移随转速分岔的计算结果，取混沌和周期解的跳跃点附近位置，即无量纲转速Ω=1.35，除齿侧间隙外其他参数保持不变，研究传动系统啮合线位移随齿侧间隙变化的分岔现象，计算结果如图6 所示.

图6 无量纲啮合线位移随齿侧间隙变化的分岔图Fig.6 Bifurcation diagram of non-dimensional action line displacement changing with backlash

由图可见:齿侧间隙在0. 5 × 10-5～3. 35 ×10-5m 之间时，系统为单周期运动;当齿侧间隙在3.35 ×10-5～3.75 ×10-5m 时，系统为两周期运动;当齿侧间隙在3.75 ×10-5～3.85 ×10-5m 时，系统通过倍周期分岔做4 周期运动，之后系统通过激变进入混沌运动，如齿侧间隙在3.85 ×10-5～8.21 ×10-5m 区间时，系统的振动突然增大，且系统运动没有规律;当齿侧间隙在8.21×10-5～9.92×10-5m 之间时，系统具有丰富的分岔特性，包含倍周期倒分岔、长周期运动，且齿侧间隙为9.92 ×10-5m 时，系统发生激变进入混沌运动，并且一直持续下去.

研究结果表明，高重合度齿轮传动系统在较小的齿侧间隙内做周期运动，系统运行平稳.进行高重合度齿轮传动系统设计时，在保证齿轮润滑的同时应选择适当的齿侧间隙，对降低齿轮传动系统的振动和噪声具有重要的意义.

4.3 阻尼比对传动系统分岔特性的影响

图7 为无量纲啮合线位移随啮合阻尼比变化的分岔图，其中齿侧间隙b=4×10-5m，转速Ω=1.35.

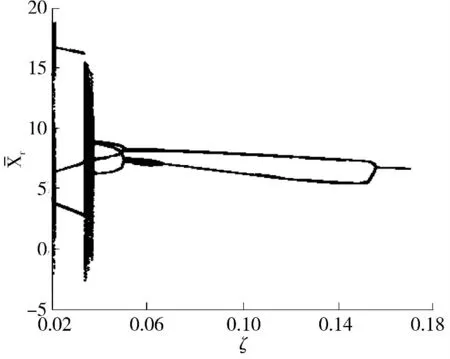
图7 无量纲啮合线位移随阻尼比变化的分岔图Fig.7 Bifurcation diagram of non-dimensional action line displacement with the change of damping ratio

由图可见，随阻尼比的增加，高重合度齿轮传动系统出现了倒分岔、周期运动和混沌运动间的激变现象.当阻尼比ζ 为0.020 ～0.036 时，齿轮传动系统经短暂混沌运动后通过激变进入3 周期运动，然后通过激变重新进入短暂的混沌运动状态. 当阻尼比ζ 为0.037 ～0.170 时，系统表现为周期运动，系统由4 周期运动经3 次倒分岔进入稳定的单周期运动，可知该阻尼比范围内系统运动状态的变化较平缓.因此，大阻尼HCR 齿轮传动系统具有较高的周期运动稳定性，增加阻尼比可降低传动系统的振动和噪声.

4.4 支撑间隙对传动系统分岔特性的影响

无量纲转速Ω=1.34，当b1=0 时，无量纲啮合线位移随从动齿轮的支撑间隙变化的分岔图如图8(a)所示，图8(b)为b2=0 时无量纲啮合线位移随主动齿轮的支撑间隙变化的分岔图.

从动齿轮的支撑间隙对齿轮的分岔特性影响较大.在较小的支撑间隙作用下，系统做3 周期运动，当间隙超过3.3 ×10-6m 时，系统通过激变进入混沌运动，而主动间隙的变化对系统运动状态的影响较小，其一直做稳定的3 周期运动.

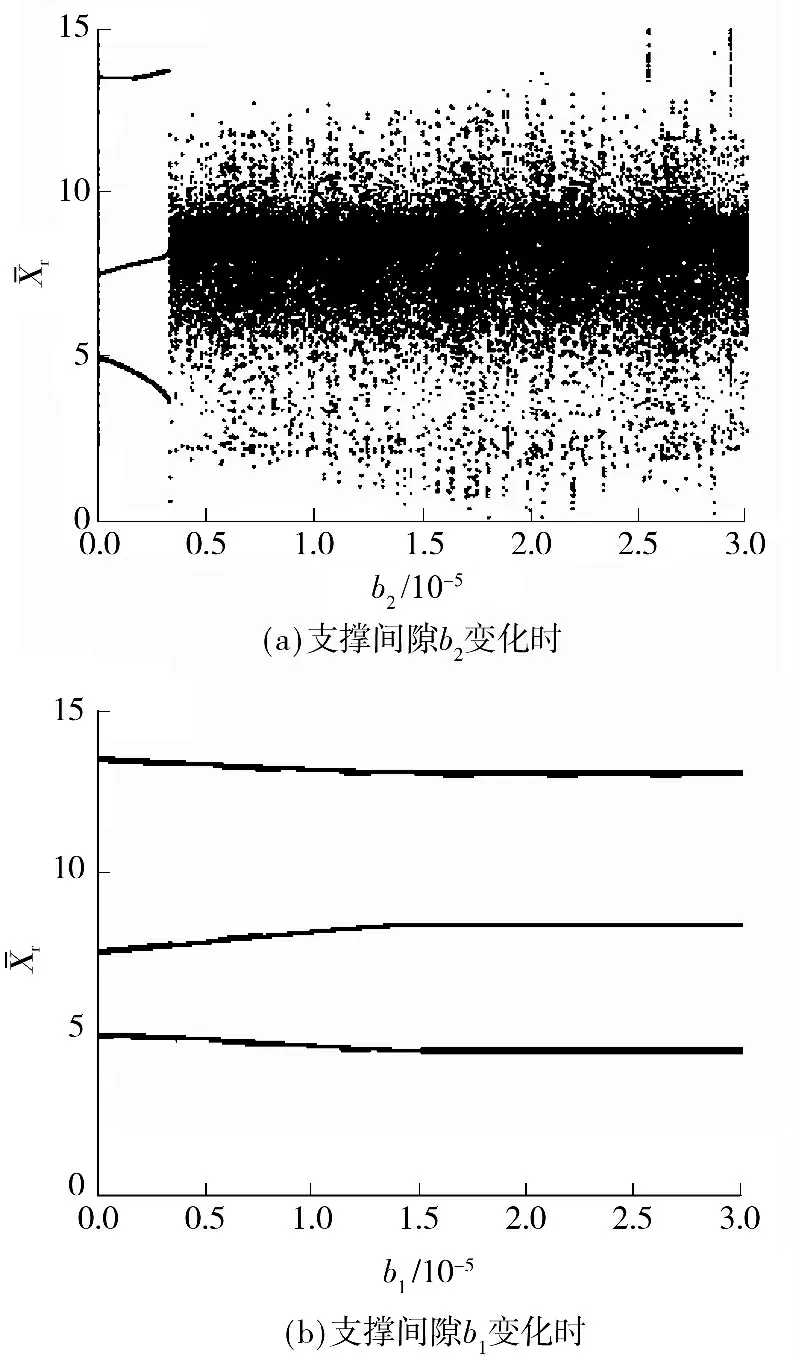
图8 支撑间隙b2、b1 变化时的分岔图Fig.8 Bifurcation diagram of system changing with b2 and b1

主动齿轮的轴承支承间隙对系统动力学的影响比从动齿轮轴承支承间隙的影响要显著. 在满足轴承润滑的同时，选择较小的轴承支承间隙，可以使系统在周期范围内运行，有效减小齿轮传动系统的振动和噪声.

5 齿轮传动系统的稳定性

齿轮传动系统运动状态复杂，当系统处于跳跃点转速附近运行时，即使系统运行参数发生轻微的波动，系统也很容易进入失稳状态［20］，图9 为啮合线位移的跳跃变化，参数同4.1 节.

由图9 可见:当Ω 为0.30 和0.44 时，系统的解发生了较小的跳跃，图3 对应位置出现了少量离散点;当Ω 为0.68 ～0.74 时，系统发生了两个稳态解的跳跃，对应的分岔图为两周期运动;当Ω 为1.07 ～1.40 时，系统发生了复杂的跳跃行为，这表明在该转速下，啮合线位移受初始参数影响较大，系统运行轨道不可预见;当Ω 为1.68 ～1.90 时，啮合线位移具有多周期性和混沌性;当Ω 大于1.90 时，其运行规律与图3 所示分岔特性相吻合.

图9 啮合线位移跳跃图Fig.9 Jump phenomenon on action line

高重合度齿轮传动系统在单周期运动下运行稳定连续，在混沌区域发生剧烈的跳跃，在多周期区域发生跳跃后运行于某一周期轨道. 系统的跳跃与相同参数下的分岔图具有较好的对应关系，齿侧间隙变化和阻尼变化对系统造成的跳跃影响将不再做分析.

当转速运动于跳跃点附近和混沌运行区域时，高重合度齿轮传动系统的运动参数发生轻微改变，系统的啮合线位移解¯Xr发生剧烈跳跃，从而增加齿轮传动系统振动的不确定性和强度，因此在设计齿轮运行参数时，需避开系统的跳跃点和混沌运行区域的位置.

6 结论

文中建立了含轴承支撑间隙的HCR 齿轮传动系统的动力学模型，基于功能原理建立了齿轮传动系统的能量方程，并对方程进行了无量纲化处理，采用4 阶Runge-Kutta 对方程进行求解，研究了HCR齿轮传动系统的动力学分岔和跳跃特性，主要结论如下:

(1)HCR 齿轮传动系统在时变啮合刚度、间隙、弯扭耦合等因素影响下，具有丰富的分岔特性，随着运动参数的变化出现了单周期、倍周期、多周期和混沌等运动状态;系统通过激变途径进入混沌运动.

(2)随齿侧间隙增加，系统经历了单周期运动、倍周期运动、混沌运动.小齿侧间隙对高重合度齿轮传动系统运动状态影响较小，齿轮传动系统处于周期运动，系统运行平稳.

(3)小阻尼比情况下，系统处于混沌和周期运动的激变区域，期间要经过两次混沌运行区域;较大阻尼比下，系统运转较为平稳，系统由4 周期运动经3 次倒分岔进入稳定的单周期运动.

(4)从动齿轮支撑间隙对系统运动状态的影响较大，主动齿轮支撑间隙影响较小.

(5)在混沌区域，系统啮合线位移解发生严重的跳跃现象，因此应选择合适的运动转速，避开系统的混沌运动区域和跳跃点位置，从而有效降低齿轮传动系统的振动.

［1］Tuplin W A.Gear tooth stresses at high speed［J］.Proceedings of Institution of Mechanical Engineers，1950，16(9):162-167.

［2］仙波正莊.高强度齿轮设计［M］.北京:机械工业出版社，1981.

［3］Harris S L.Dynamic loads on the teeth of spur gears［J］.Proceedings of the Institution of Mechanical Engineers，1958，172:87-112.

［4］Ozguven H N，Houser D R.Mathematical models used in gear dynamics:a review［J］.Journal of Sound and Vibration，1988，121(3):383-411.

［5］Benton M.Simulation of resonances and instability conditions in pinion-gear systems［J］.ASME Mech Des，1978，100:26-35.

［6］Kahraman A，Blankenship G W.Interactions between commensurate parametric and forcing in a system with clearance［J］. Journal of Sound and Vibration，1996，194(3):317-336.

［7］Kahraman A，Singh R.Nonlinear dynamics of a spur gear pair［J］.Journal of Sound and Vibration，1990，142(1):49-75.

［8］Tamminana V K，Vijayakar S，Kahraman A.A study of the relationship between the dynamic factors and the dynamic transmission error of spur gear pairs［J］. Journal of Mechanical Design，2007，129(1):75-84.

［9］Li Shuting. Effect of addendum on contact strength，bending strength and basic performance parameters of a pair of spur gears［J］. Mechanism and Machine Theory，2008，43:1557-1584.

［10］Liou Chuen-Huei，Lin Hsiang His，Oswald Fred B，et al.Effect of contact ratio on spur gear dynamic load［R］.［S.l.］:Memphis State Un:versity，1992.

［11］Thirumurugan Rama，Muthuveerappan G.Critical loading points for maximum fillet and contact stresses in normal andhigh contact ratio spur gears based on load sharing ratio［J］.Taylor ＆ Francis，2011，39:118-141.

［12］Wang Jiande，Howard Ian.Finite element analysis of high contact ratio spur gears in mesh［J］.ASME，2005，127:469-483.

［13］渠珍珍.高重合度行星齿轮传动系统设计及动力学分析［D］.南京:南京航空航天大学机电学院，2011.

［14］渠珍珍，鲍和云，朱如鹏，等.高重合度行星齿轮传动系统动态特性分析［J］. 机械科学与技术，2012，31(7):1174-1179.Qu Zhen-zhen，Bao He-yun，Zhu Ru-peng，et al. Dynamic characteristics analysis of high contact ratio planetary gear transmission［J］.Mechanical Science and Technology for Aerospace Engineering，2012，31(7):1174-1179.

［15］方宗德，蒋孝煜，宋镜瀛. 大重合度齿轮的性能研究［J］.齿轮，1987，11(1):27-32.Fang Zong-de，Jiang Xiao-yu，Song Jing-ying. Performance study of high contact ratio gear［J］.Gear，1987，11(1):27-32.

［16］王三民，纪名刚.高速大重合度直齿圆柱齿轮的齿廓最佳修形研究［J］.航空学报，1996，17(1):121-124.Wang San-min，Ji Ming-gang. Study on the best profile modification of high-speed spur gears with high contact ratio ［J］. Acta Aeronautica Et Astronautica Sinica，1996，17(1):121-124.

［17］刘梦军.单对齿轮系统间隙非线性动力学研究［D］.西安:西北工业大学机电学院，2002.

［18］胡海岩.应用非线性动力学［M］.北京:航空工业出版社，2000.

［19］李发家，朱如鹏，鲍和云，等.行星齿轮系动力学特性分析及试验研究［J］.南京航空航天大学学报，2012，44(4):511-519.Li Fa-jia，Zhu Ru-peng，Bao He-yun，et al.Study on dynamic characteristics and experiment research of planetary gear system ［J］. Journal of Nanjing University of Aeronautics ＆ Astronautics，2012，44(4):511-519.

［20］李同杰，朱如鹏，鲍和云，等.行星齿轮系扭转非线性振动建模与运动分岔特性研究［J］.机械工程学报，2011，21(47):76-83.Li Tong-jie，Zhu Ru-peng，Bao He-yun，et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train［J］.Journal of Mechanical Engineering，2011，21(47):76-83.