数形结合,让算理与算法交融
王芳


算理和算法在计算教学中相辅相成,缺一不可。算理和算法又十分抽象,对于以直观形象思维为主的小学生来说是学习的难点。数形结合思想是通过数与形的相互转化,将抽象的数学语言与直观的图形结合起来解决问题的思想方法。有效运用数形结合的思想方法可以化抽象为直观,帮助学生理解算理和掌握算法,提高计算教学效率。下面以“分数乘分数”一课为例谈谈具体的做法。
一、以形解数,感知算理
基于学生的生活经验和思维,分数乘分数计算的算理和算法对于他们来说很抽象、难以理解的。所以,为分数找对应的图形,以图形来表达分数,解释其中的算理,使学生在直观操作中理解算理。
【片断一】
1.探究1/2 ×1/4
师:像1/2 ×1/4 这样的分数乘分数问题怎样研究呢?如果用一个长方形表示“1”,那么怎样画图表示出算式中的分数?请同学们试一试。
师:画图时先分了什么,表示了哪个分数?
生:先把单位“1”平均分成2份,取这样的1份。
师:接着怎么分的?又取了几份?
生:再把这一份平均分成4份,取其中的1份。
课件演示:
师:通过画图我们知道了1/2 ×1/4 实际上是求1/2 的1/4 是多少。那1/2 的1/4 到底是多少呢?是怎么知道的?
生:只要把刚才平均分的虚线画下去,也就是把空白部分一起平均分,就能看出是1/8 。
师:8在哪里?1在哪里?
2.探究1/2 ×3/4
师:怎样在长方形图中表示出1/2×3/4?请大家画画看。
学生反馈:
师:1/2 的3/4 积是多少呢?怎样修改这幅图?
生:只要把整个大长方形竖着平均分成4份,整个大长方形一共平均分成了8份,所以1/2×3/4 =3/8 。
【教学分析】
在探究算理的过程中,以长方形作为探究材料。第一次让学生尝试画图,理清画图的方法,得出“分了取,再分再取”的画法,“以形助数”,使学生理解1/2×1/4 = 1/8 是怎样得到的;第二次画图则更注重以形解数,在追问中让学生感知1/2×3/4 = 3/8 中3/8 的算理。两次经历从数到形,再从形抽象出数的过程,学生初步感知了算理。因此,在探究算理时,先教给学生准确的画图方法,再引导学生以形解数,层层递进来感知算理。
二、以数思形,深化算理
画图操作初步理解算理后,常会发现学生很难用完整的数学语言对操作的结果加以提炼和概括,主要是因为学生由动手操作到抽象概括缺少了“表象”这一支撑点。儿童的认识规律,一般是从直接感知到表象,再到形成科学概念的过程,表象介于感知和形成科学概念之间,所以需要帮助学生建立这个支撑点,引导学生由具体思维合理地向抽象思维转化,从而深化算理。
【教学分析】
在深化算理的环节中,教师让学生静静地“想一想,先画什么?再画什么?”看似多余的一个过程却非常有必要。因为“分数乘分数”算理模型的构建从具体思维向抽象思维转化,对于学生来说是具有难度的,如果没有留给学生一个思考的空间,没有借助“在脑中画图”这种半具体半抽象的表象操作,那么一些学生难以实现从形象思维到抽象思维的有效转化。
三、以数质形,向算法过渡
算理是算法的依据,它保证了计算的合理性和正确性;而算法是算理的概括,它为计算提供了快捷的操作方法。学生只有真正理解了算理和算法,才能灵活、准确地进行计算。因此,在对算理有了较深的理解后,要帮助学生从算理过渡到算法。
四、数形互释,生成算法
算理和算法是计算教学中不可分割的两个方面,只有实现算理和算法的相互交融,才能促进算法的有效生成。那么如何沟通“数”与“形”之间的联系,促进算理和算法的交融,让学生更进一步明晰“分母相乘、分子相乘”这一算理,从而有效生成算法呢?
【片断二】
1.师:如果按照刚才的想法,3/5×4/7 怎样计算?
生:5乘7作分母,3乘4作分子,积是12/35 。
师:我们利用长方形图来验证一下,该怎么分怎么取?
生:先把这个长方形横着平均分成5份,取3份;再竖着平均分成7份,这样一共平均分成了35份。
师:再取4份,最终取了多少份?
生:最终取了12份。所以3/5 ×4/7 的积是12/35
2.师:只验证一题,还不能够说明。换一题再试一试,行吗?
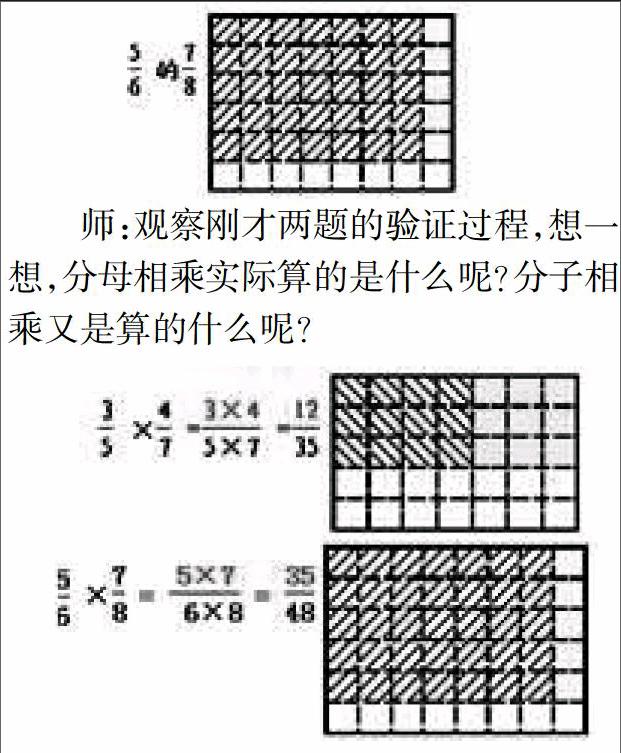
出示:5/6 ×7/8
师:从图中你知道了什么?
生:6×8算的是把整个长方形一共平均分成了多少份,5×7算的是最终取了多少份。
师:观察刚才两题的验证过程,想一想,分母相乘实际算的是什么呢?分子相乘又是算的什么呢?
生:分母相乘是求把单位“1”平均分成的份数,分子相乘就是取的份数。
师引导学生自主归纳出“分母相乘就一共分了多少份,分子相乘表示一共取了多少份”。
【教学分析】
上述教学中教师紧紧抓住引导学生验证的过程,通过数形互释,打通了算理和算法之间的联系,有效促进算理和算法的相互交融。用“数解释形” ,让学生明白一共35份是指把整个长方形平均分成了5行7列,5×7就是35份;最终取了3×4=12份。由“形解释数” ,使学生清晰了6×8算的是把整个长方形一共分成了48份,5×7算的是最终取的35份,从而自然得出“分数乘分数,分母相乘的积作分母,分子相乘的积作分子”的计算方法。学生再次经历了自主验证的过程,通过观察、比较、验证、归纳,在算法形成与巩固的过程中进一步明晰算理,在真正理解算理的基础上掌握算法,从而形成计算技能。再次利用图形来沟通算理和算法的联系,在数形互释中进一步理解算理和掌握算法,使学生对计算方法做到知其然,更知其所以然。
在计算教学中,有的放矢地运用数形结合思想方法,为学生构建一个算理算法交融的课堂,引导学生在算法探究中理解算理,在理解算理的基础上形成算法,那么计算课堂同样会是精彩的。
【作者单位:太仓市城厢镇第四小学 江苏】

