考虑邻道干扰条件下的Ad Hoc网络性能分析及优化

颜伟光，李文泽

(1.江苏食品药品职业技术学院信息工程系，江苏淮安223003;2.河南广播电视大学理工学院，河南郑州450008)

连续相位频移键控(Continuous Phase Frequency Shift Keying，CPFSK)［1］和跳频(Frequency Hopping，FH)频谱扩展技术［2］经常同时使用于 Ad Hoc网络中［3］。在 CPFSK跳频Ad Hoc网络中，尽管CPFSK信号具有频谱紧凑的特征，依然有部分信号功率不可避免地散射到相邻的频率信道上，从而造成邻道干扰(Adjacent Channel Interference，ACI)问题［4］。因此，分析网络性能时需要考虑ACI问题对网络的影响。

传输容量是分析网络性能的主要指标，主要衡量网络空间频谱利用效率［5］。文献［6］分析了系统最大传输容量与调制指数、编码速率和信道数目等参数的关系。其中，CPSFK的频谱效率以带宽内能量的百分比作为衡量标准。关于CPFSK调制方式的频谱效率，文献［6］提出频率信道带宽内含有99%的信号功率，这意味着1%的信号功率散射到相邻信道带宽，即产生了ACI问题，但现有相关文献并未深入分析ACI对系统性能的影响。

此外，当信道带宽固定时，增加比特传输速率会降低部分带内功率，增加散射到相邻信道上的信号功率。尽管ACI会严重影响性能，但可以通过增加比特传输速率以获得较低速率的纠错编码，进而获得部分性能增益。因此，在分析网络传输容量时，量化部分带内功率对系统性能的增益也需要考虑ACI问题。

针对CPFSK跳频Ad Hoc网络，在阴影和Nakagami衰落条件下，本文提出了一种考虑ACI问题的网络性能分析方法，并建立了相应的网络模型。通过该方法推导出了条件中断概率、空间平均中断概率和传输容量等性能标准的数学表达式。最后，基于ACI分析模型，使用Nelder-Mead单纯形方法优化网络传输容量，给出了网络的最优传输容量参数配置。优化结果验证了该分析方法的有效性。

1 Ad Hoc网络模型

本节假设Ad Hoc网络发送节点和接收节点均使用CPFSK调制方式和跳频模式。设Ad Hoc网络中包含M+2个移动节点，其中有1个参考接收节点位于原点，还有一个参考发送节点X0和M个干扰节点X1，X2，…，XM。变量Xi表示移动节点i和其位置，并且 Xi表示节点Xi距接收节点的距离。干扰节点位于内半径为rex和外半径为rnet的环形区域内，环形区域面积为在参考接收机端，Xi节点功率［7］为

式中:d0表示参考距离;Pi表示发射功率;gi指衰落功率增益;ξi指阴影系数;α＞2为衰减功率指数，并且有表示参数为mi的Nakagami分布。

网络采用适用于慢跳频系统的信道接入协议［8］。设每跳持续周期内衰落功率增益{gi}为恒定值，并且跳与跳之间相互独立，每个发送节点到接收节点的信道均有一个独立的Nakagami参数mi。可用频谱带宽B划分为L个连续的频率信道，信道带宽为B/L。发送节点以相等概率选择发送信道，其中源节点X0选择位于频谱边缘的信道发送信号的概率为2/L，而选择非边缘信道的概率则为L-2/L。且有Di≤1表示Xi的占空因子，为节点发送信号的概率。

设pc和pa分别表示同信道冲突和邻道冲突［9］发生的概率，每个节点的Di=D均为常数。如果干扰节点Xi发送信号时，其选择和发送节点使用相同频率的概率为1/L。因此，干扰节点Xi引入相同信道干扰冲突的概率为pc=D/L。当源节点x0使用边缘信道时，干扰节点Xi选择与之相邻信道的概率为1/L，而当源节点使用非边缘信道时，其相邻信道有2个，则干扰节点选择相邻信道的概率为2/L。因此，对于一个随机选择的信道，节点Xi引入邻道冲突的概率为

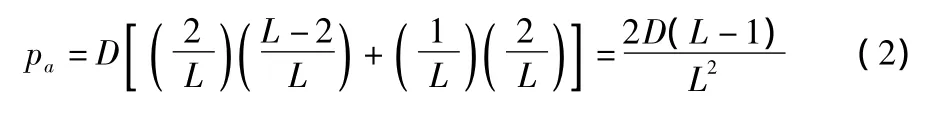
信号发送过程会有部分功率散射在所选择信道之外，设ψ为部分带内功率，一般满足0.95≤ψ≤0.99。文中假设邻道功率散射比Ks(1-ψ)/2，表示散射到发送信道相邻信道的信号功率。根据上述模型，接收机端的瞬时信干噪比(Signal Interference Noise Ratio，SINR)［10］为

式中:n0是白噪声功率，离散随机变量Ii为

式中:pI为Ii对应取值的概率，不发生冲突的概率pn满足pn=1-pc-pa=1-D(3L-2)/L2。将式(1)带入式(3)，则

2 中断概率性能分析

基于上述网络模型，本节分别推导出了CPFSK跳频Ad Hoc网络的条件中断概率和空间平均中断概率的数学表达式。

2．1 条件中断概率

设β为分组可靠接收需要的最小SINR值，Ω={Ω0，Ω1，…，ΩM}则表示所有发送节点Xi的归一化接收功率集合。当SINR小于β时则会产生中断，故当条件为Ω时，中断概率有

其次，定义变量Z有

故条件中断概率为

式中:Γ-1为条件为Ω时Z的累积分布函数 CDF。同时，设表示条件为Ω时Z的互补累积分布函数，并设整数m0表示信号独立衰落，据文献［11］可得

其中，β0=βm0/(ψΩ0)，且有 Hk(Ω)为

式(10)中，Gli(Ωi)为

其中，fYi(y)为Yi=IigiΩi的概率密度函数PDF。考虑Nakagami衰落和Ii统计数，Yi的概率密度函数为

其中，u(y)为单位阶跃函数，δ(y)是Dirac delta函数。将式(12)代入(11)，得

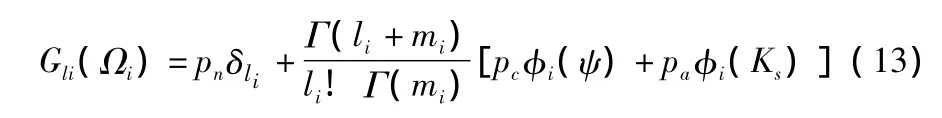
其中δli是Kronecker delta函数，并且有

2．2 空间平均中断概率

假设干扰节点位置在干扰区域内服从独立和均匀分布，且干扰节点服从密度λ=M/A的二项点过程(Binomial Point Process，BPP)过程［12］。设 ε(λ)为相应的空间平均中断概率，是关于Ω的Fz(Γ-1Ω)函数的期望，为

首先，设系统没有阴影，即对于所有i有ξi=0和固定位置X0，故而β0和Ω0均为常数。基于式(15)，Z的互补累积分布函数为

其中，EΩ{Hk(Ω)}为

由于所有干扰节点均在环形区域内均匀分布，因此对于{Ωi}，i=1，2，…，M，有概率密度函数为

其中，有 ci=(Pi/P0)。结合式(17)，(18)，有

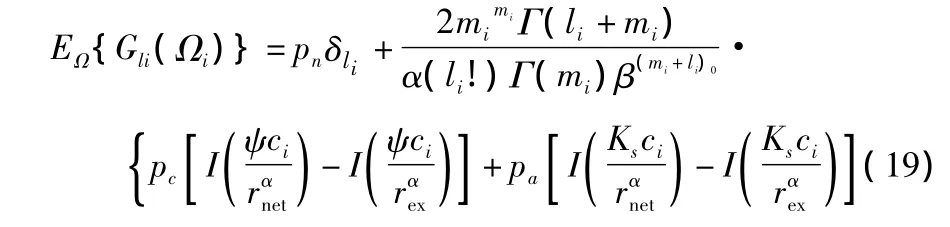
其中，有I(x)为

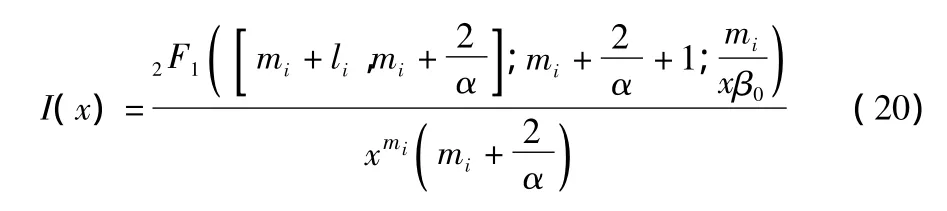
其中:2F1(·)是高斯超几何函数［13］。

3 基于CPFSK调制受限的传输容量分析

空间平均中断概率 ε(λ)通常满足 ε(λ)≤ζ，且 ζ∈［0，1］。因此，使用传输容量(Transmission Capacity，TC)表示最大传输密度［14］。TC代表空间频谱利用效率，例如单位区域内传输成功的数据速率。空间平均TC可由λ和 ε(λ)表示，有

如文献［15］中所述，传输容量是SINR门限的β函数，并且计算时不需要假设调制类型和信道编码。实际中，β是系统使用的调制方式和信道编码的函数。设C(γ)为最大可获得速率，由瞬时SINR，即γ和所选择的调制方式决定。如果使用系统可达到最大速率R的编码，则当C(γ)≤R会产生中断。当信道为块衰落信道，SINR门限为 β=C-1(R)的中断概率能够提供码字错误速率的精准预测。文献［16］给出了非相干接收CPFSK对于不同h的对称信息速率值，其通过计算非相干AWGN信道输入和输出的平均互信息获得。

最大数据传输速率由信道带宽B/L、部分带内功率ψ、调制方式的频谱效率和编码速率等确定。设η表示调制方式的频谱效率，单位为symbol·s-1·Hz-1，由符号速率除以调制方式功率带宽100ψ%获得。为了强调η相对于h和ψ的相关性，用η(h，ψ)表示CPFSK频谱效率。结合速率为R的编码，频谱效率为 Rη(h，ψ)，单位 bit·s-1·Hz-1，其中 R 是信息比特和码字符号比率。由于信号带宽效率为100ψ%，并且带宽为B/L(单位Hz)，故在占空因子为D的单链路支持条件下的最大数据速率为

将式(22)代入式(21)并除以系统带宽B得到归一化的空间平均调制受限传输容量(Modulation Constrained Transmission Capacity，MCTC)

和式(21)相比，此式的传输容量表达式精准考虑了编码速率R、调制方式的频谱效率和频率信道数目等参数。

4 Ad Hoc网络优化

4．1 仿真平台环境

本节使用 θ=(L，R，h，ψ)，C(θ)，表示单目标优化函数，求解具有最小值目标函数值条件下的最优θ。文中设定λ为固定值，用 τ'(θ)表示归一化 MCTC，这里求最小 C(θ)=-τ'(θ)以获得归一化MCTC最大化。本节使用MATLAB 2012对系统性能进行数值计算，并使用OPNET14.5网络仿真软件构建Ad Hoc网络。其中，4.2和4.3节部分性能参数设置相同，具体如下:网络环形区域内半径rex=0.25，M=50为潜在干扰节点数目，D=1，源节点和接收节点距离 X0=1，路径损耗指数α=3，信噪比Γ=10 dB。

4．2 全面评估

以某典型参数配置为依据，示例系统余下参数设置如下:环形区域外半径rnet=2，阴影方差σs=8 dB，干扰节点分布位置服从分布密度为λ=50/(π(22-0.252))≈4的BPP分布，混合衰落模型参数m0=4，且mi=1，i≥1。频谱散射考虑3种情况:无散射，最小频谱散射(ψ=0.99)和适度频谱散射(ψ=0.96)。当不考虑频谱散射时，计算η时使用CPFSK的99%功率带宽，pa=0。当考虑频谱散射时，计算η时使用CPFSK的100ψ%功率带宽，同时利用式(2)计算pa。MCTC性能仿真时，主要自变量范围满足 L∈［1，200］，R∈(0，1)，单位增量 ΔR=0.01，h∈(0，1］，Δh=0.01。

因为τ'(θ)参数是4维，图1给出了MCTC在不同ψ时随信道数目L变化的性能曲线，其中参数R和h取最大化τ'(θ)条件下的值。为了突出优化结果与个别自变量之间的函数关系，有目标优化函数τ'opt(Lψ)为

图1 网络MCTC性能随信道数目L变化曲线示意

由图1可知，当考虑频谱散射且ψ=0.99，系统性能有一定下降。但是当频谱散射程度增加，即ψ=0.96，性能反而有所提升。这说明了联合优化ψ和其他参数将获得潜在系统增益。此外，当时30≤L≤50，系统能够获得最大化MCTC。

4．3 基于单纯形的网络性能优化

当离散化θ集合很大时，τ'(θ)的全面评估计算非常密集，特别是当Nakagami因子m0取值很大时，并且由于τ'(θ)是基于θ的非线性函数，很难推导出理论公式。因此，本节使用Nelder-Mead单纯形优化方法［17］寻优。

在四维优化问题寻优中，使用Nelder-Mead方法构造五维单纯形作为初始解集。每次迭代过程中，计算每个顶点的目标函数值，然后反复替换单纯形中目标函数值最大的顶点。本文问题寻优中，单纯形第一个顶点初始化(Le，R，h，ψ)=(20，0.5，0.5，0.975)，其他顶点距第一个顶点距离分别为 1，0.025，0.025 和 0.005。设 θ1，θ2，…，θ5表示单纯形的各个顶点，有:C(θ1)≤C(θ2)≤…≤C(θ5)。迭代过程中，通过沿着单纯形表面反射θ5来产生备用顶点θr并计算其目标函数值。如果有 C(θ1)≤C(θr)≤C(θ4)，则用 θr代替顶点 θ5。所有顶点将再次根据目标函数值进行排序并再次使用上述迭代流程。如果C(θr)≤C(θ1)，则通过将θr到其他4个顶点定义的表面之间的距离双倍以实现单纯形扩展操作，进而产生另一个备用顶点 θs。如果 C(θs)≤C(θr)，则用 θs替换 θ5来完成扩展操作，否则仍用 θr代替顶点 θ5。如果 C(θs)≤C(θr)，则通过将Max(θ5，θr)和其他4个顶点构成的表面之间的距离缩小一半的方法完成压缩操作，如果新顶点的目标函数值小于当前值则接受压缩操作。否则，如果上述条件均不满足，则最小值必然存在于单纯形内，通过依次减小各边长度寻找到最优解。

通过使用Nelder-Mead单纯形优化算法，得到了干扰节点服从λ密度BPP分布条件下的最优化结果。除和4.2部分参数设置相同以外，其他参数设置如下:环形区域外半径取值rnet=2，4，分别对应不同节点分布密度λ≈4，1。同时考虑3种衰落模型和2种阴影环境:瑞利衰落模型(mi=1，i≥1)，Nakagami衰落(mi=4，i≥1)，和混合衰落(m0=4，mi=1，i≥1)，无阴影环境(σs=0 dB)，阴影环境(σs=8 dB)。

图2给出了rnet=2和σs=8 dB条件下3种不同衰落模型中最优传输容量随ψ的变化曲线，其中(L，R，h)参数取最优结果相应的值。据图2可知，3种衰落模型条件下，当ψ=0.96时能够取得最优网络传输容量。在混合衰落模型环境下，当 ψ =0.96 时，有{L，R，h}={38，0.64，0.81}。当由于频谱散射造成的ACI忽略并使用99%的带宽功率时，混合衰落环境下有优化参数值为{L，R，h}={24，0.68，0.59}。因此，当考虑由频谱功率散射引起的ACI邻道自干扰时，较大的频率信道数目L和调制因子h将提供更优的网络传输容量。

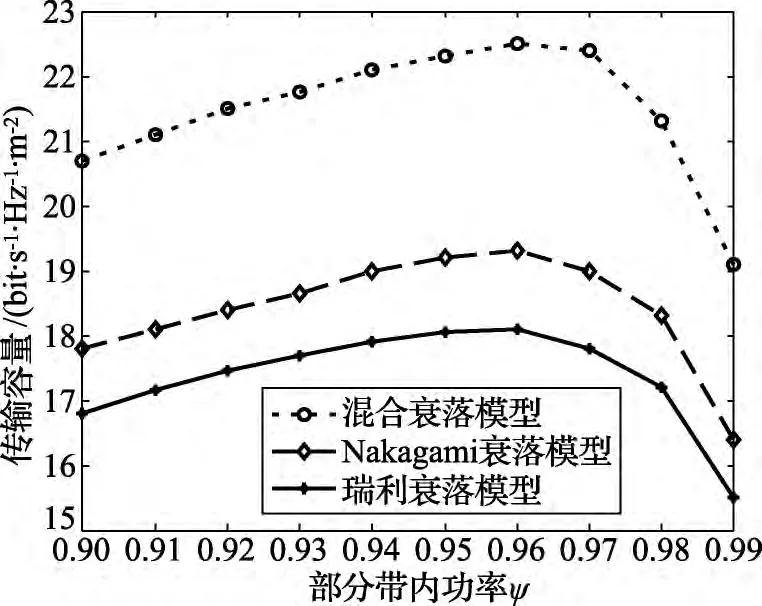
图2 网络传输容量随部分带内功率的变化曲线

表1给出了2种网络覆盖区域、3种衰落模型和两种阴影环境下的优化参数和结果数值。据表1可知，rnet=2和rnet=4网络性能最大化时最优部分带内功率分别为ψ=0.96和ψ=0.95。对于瑞利信道，轻微阴影环境可以提升网络性能，但对于Nakagami和混合衰落模型而言，轻微阴影环境会降低网络性能。此外，增加网络节点布密度，可以增加传输容量，但需要更大的L，R和ψ，以及更小的h。

表1 不同条件下的网络优化结果和参数值

5 结束语

CPFSK跳频Ad Hoc网络中，网络性能主要取决于调制因子、编码速率、频率信道数目和部分带内功率等因素。本文提出了一种考虑邻道干扰条件下的CPFSK跳频Ad Hoc网络性能分析方法，给出了网络模型、中断概率和传输容量数学表达式。并在考虑阴影、衰落等环境的基础上利用单纯形优化方法给出了网络传输容量最大时的参数配置。优化结果验证了分析方法的有效性。

［1］沙楠，高媛媛，益晓新，等.基于连续相位频移键控调制的物理层网络编码检测及性能分析［J］.电子与信息学报，2014，36(6):1453-1459.

［2］李苏阳，全厚德，崔佩璋.图样匹配跳频系统的性能及图样码型选择［J］.计算机工程与设计，2013，34(7):2367-2371.

［3］ OLUWATOSIN A，JOHN M.Iterative channel estimation and partially coherent demodulation of CPFSK in Time-selective fading channels［C］//Proc.2011 Military Communication Conference.［S.l.］:IEEE Press，2011:323-328.

［4］ MATTHEW C V，SHIC，DON T.Iterative multi-symbol non-coherent reception of coded CPFSK［J］.IEEE Trans.Communications，2010，58(7):2046-2054.

［5］唐菁敏，倪晨泉，杨孟，等.具有保护区域的无线Ad Hoc网络传输性能研究［J］.电子科技大学学报，2014，43(4):519-523.

［6］ VALENTI M，TORRIERI D，TALARICO S.Optimization of a finite frequency-hopping Ad Hoc network in Nakagami fading［C］//Proc.IEEE Military Communication Conference. ［S.l.］:IEEE Press，2012:1204-1216.

［7］倪志，李道本.非理想信道估计和相关Nakagami信道条件下空时发送分集的性能分析［J］.北京邮电大学学报，2004，27(5):37-40.

［8］高章飞，蒋正义，朱善安.基于多信道跳频的Ad Hoc网络MAC层协议研究［J］.自动化仪表，2005，26(12):5-8.

［9］ MOHAN R A，RAJAN B，MOISESS，et al.Cellular network configuration with co-channel and adjacent-channel interference constraints［J］.Computer＆Operations Research，2012，35(2):3738-3757.

［10］张豪，杨育红，朱义君，等.一种基于最大化信干噪比的通信混合信号多通道盲分离算法［J］.信息工程大学学报，2013，14(4):461-503.

［11］ TORRIERI D，VALENTI M C.The outgage probability of a finite Ad Hoc network in Nakagami fading［J］.IEEE Trans.Communications，2012，60(12):3509-3518.

［12］ DEXTER O C，FEDERICO P.On a fractional binomial process［J］.J.Stat Phys.，2012，146(3):646-662.

［13］ WOLTER G，ERIK K.A hypergeometric function transform and matrix-valued orthogonal polynomials［J］.Constr.Approx.，2013(38):277-309.

［14］孙晓惠，尹长川.基于双变量泊松点过程的无线Ad Hoc网络的保密广播传输容量分析［J］.电子学报，2014，42(9):1847-1851.

［15］ WEBER S，YANG X，ANDREWS J，et al.Transmission capacity of wireless Ad Hoc networks with outage constraints［J］.IEEE Trans.Information Theory，2005(51):4091-4102.

［16］ TORRIERI D，CHENG S，VALENTI M.Robust frequency hopping for interference and fading channels［J］.IEEE Trans.Communications，2013(56):1343-1351.

［17］高献坤，姚传安，高向川，等.解析法-Nelder Mead单纯形算法确定太阳电池参数［J］.农业工程学报，2014，30(6):97-106.