带积分边界条件的共振边值问题正解的存在性

江卫华，杨彩霞

（河北科技大学理学院，河北石家庄 050018）

1 问题提出

对常微分方程多点边值问题的研究起源于BITSADZE［1］，之后，许多学者研究了非线性多点边值问题。对多点边值问题解和正解的研究已经取得了大量的结果［2-10］。众所周知，相比非共振问题，求解共振边值问题正解的存在性相关文献报道比较少。

有学者利用Cremins半线性映射不动点指数定理［11-12］，研究了二阶常微分方程3点共振边值问题：

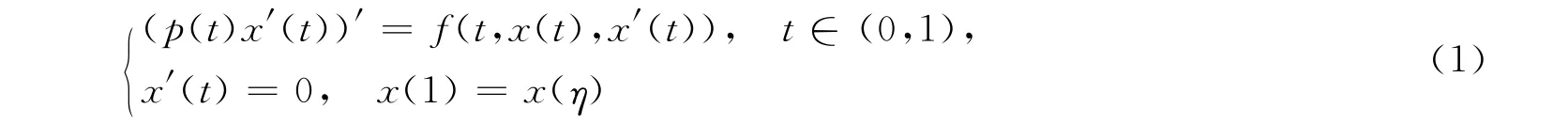
正解的存在性结果。INFANTE等［13］给出了如下共振多点边值问题：

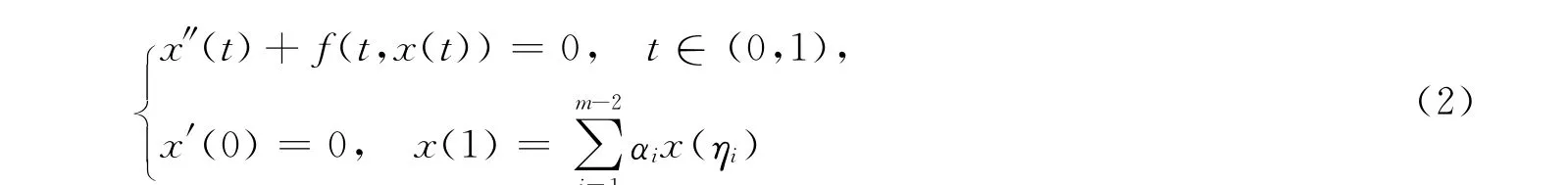
受上述文献启发，考虑如下具有积分边界条件的二阶共振边值问题：

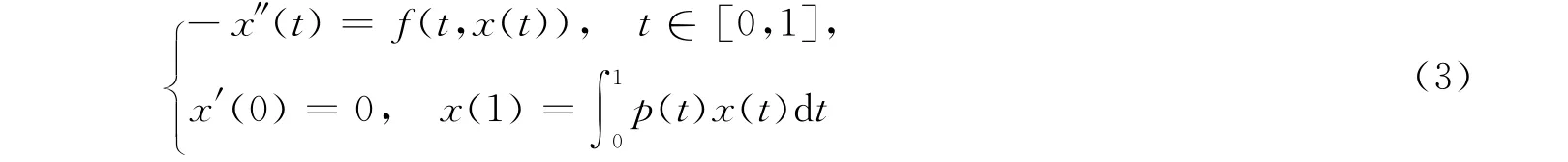
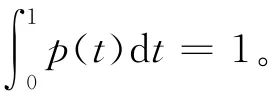
2 预备知识

为方便读者理解，在本部分开始，列出了一些基本知识以及在证明过程中必要的引理。

定义1 设X是实Banach空间。一个非空凸闭集合C⊂X如果满足：

1）λx∈C，对任何x∈C，λ≥0；

2）若x，-x∈C，则有x=θ，则称C为锥。

由C可得到X中的一个半序x≤y，当且仅当y-x∈C。

设X，Y是Banach空间，L：domL⊂X→Y是指数为零的Fredholm算子，即ImL是闭集且dim KerL=codim ImL＜∞。此时存在连续投影算子P：X→X和Q：Y→Y，使得ImP=KerL，KerQ=ImL。此外，由于dim ImQ=dim KerL，因此存在同构J：ImQ→KerL，若限制L在KerP∩domL上，记为Lp，则它的逆算子存在，记为Kp：ImL→KerP∩domL。

这样（见文献［11］、文献［12］、文献［15］和文献［16］），方程Lx=Nx等价于x=（P＋JQN）x＋Kp（IQ）Nx。

引理1［17］设C为X中一个锥，则对每个u∈C＼｛θ｝，存在1个正数σ（u）使得‖x＋u‖≥σ（u）‖x‖，对∀x∈C。

令γ：X→C为保核收缩，即γ为一连续映射，且γx=x，x∈C。并记

定理1［14］设C为X中的锥，Ω1，Ω2为X中有界开子集，且¯Ω1⊂Ω2，C∩（¯Ω2＼Ω1）≠∅。假设L：domL⊂X→Y是指数为0的Fredholm算子，且

1）QN：X→Y连续有界，Kp（I-Q）N：X→X在X的任意有界子集上是紧的；

2）对任何x∈∂Ω2∩domL，λ∈（0，1），Lx≠λNx；

3）γ将¯Ω2中子集映射为C中有界集；

4）dB（［I-（P＋JQN）γ］|KerL，KerL∩Ω2，0）≠0，其中dB代表Brouwer度；

5）存在u0∈C＼｛0｝使得∀x∈C（u0）∩∂Ω1，都有‖x‖≤σ（u0）‖Ψx‖，其中C（u0）=｛x∈C：μu0≤x，μ＞0｝，σ（u0）满足对∀x∈C，不等式‖x＋u0‖≥σ（u0）‖x‖ 都成立；

6）（P＋JQN）γ（∂Ω2）⊂C；

7）Ψγ（¯Ω2＼Ω1）⊂C。

则方程Lx=Nx在C∩（¯Ω2＼Ω1）中有1个解。

为表达简单，令易知，G（t，s）≥0，t，s∈（0，1）。令

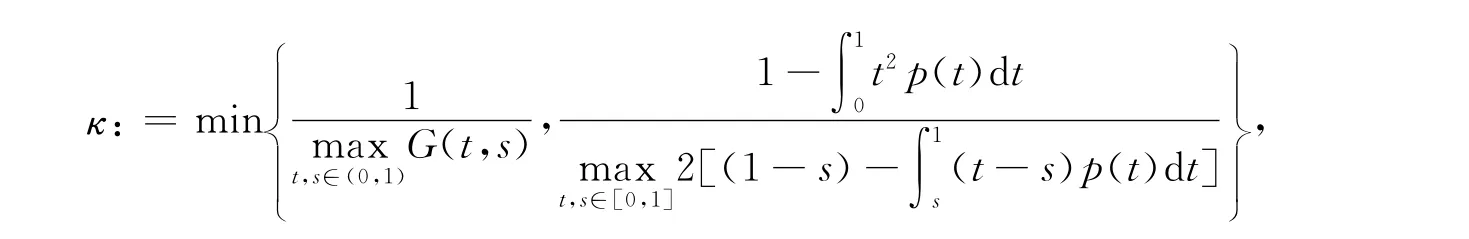
显然κ＜1。

3 主要结论

定理2 设存在R∈（0，∞）使得f：［0，1］×［0，R］→R连续且

H1）f（t，x）＞-κx，对任何（t，x）∈［0，1］×［0，R］，

H2）f（t，R）＜0，对任何t∈［0，1］，

H3）存在r∈（0，R），t0∈［0，1］，a∈（0，1］，M∈（0，1）和连续函数g：［0，1］→［0，∞），h：（0，r］→［0，∞）使得对［t，x］∈［0，1］×（0，r］，总有f（t，x）≥g（t）h（x），且h（x）／xa在（0，r］上非增并满足：

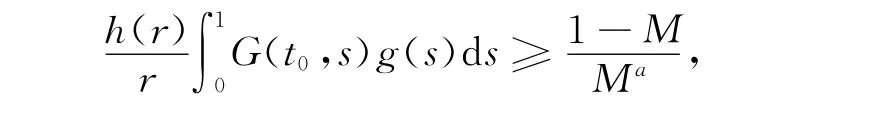
则边值问题（3）在［0，1］上至少有1个正解。

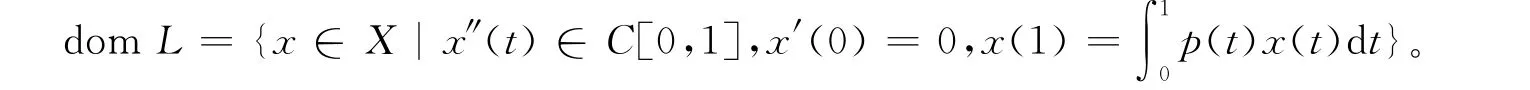
定义算子N：X→Y且（Nx）（t）=f（t，x（t）），t∈［0，1］。

显然有 KerL=｛x∈domL：x（t）=c，t∈［0，1］｝且

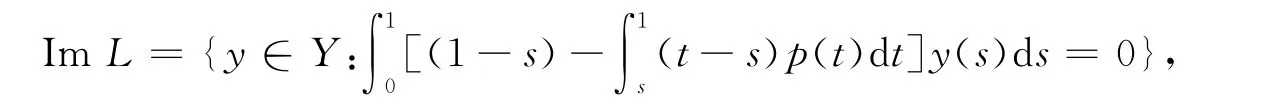
显然，dim KerL=1，ImL是闭集。

定义投影算子P：X→X，Q：Y→Y分别为

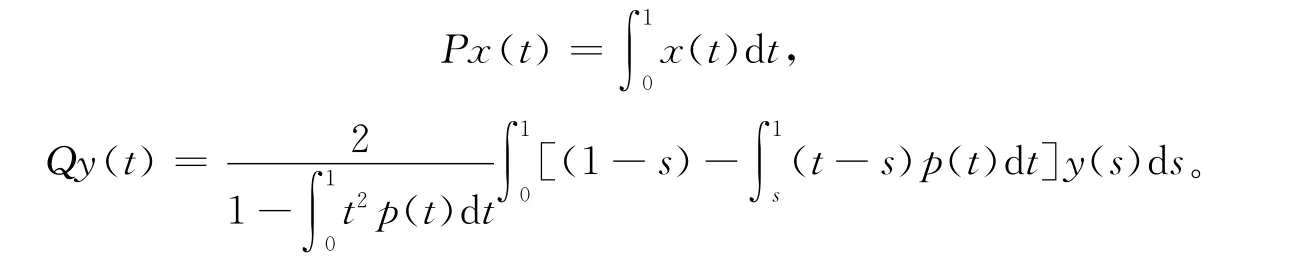
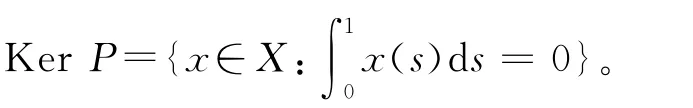
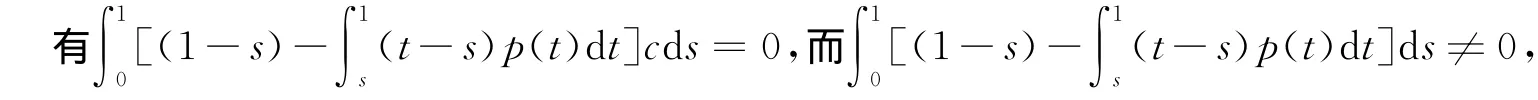
对任一y∈ImL，Lp的逆算子Kp由下式给出：

其中：

考虑到f可连续延拓至［0，1］×（-∞，＋∞），因此定理1中条件1）成立。

定义锥C= ｛x∈X：x（t）≥0，t∈ ［0，1］｝。

令Ω1= ｛x∈X：r＞|x（t）|＞M‖x‖，t∈ ［0，1］｝和Ω2= ｛x∈X：‖x‖ ＜R｝。

容易验证Ω1，Ω2为有界开集。

此外，C∩（¯Ω2＼Ω1）≠∅。定义同构J：ImQ→KerL为J=I，算子γ：X→C为（γx）（t）=|x（t）|，x∈X。在此定义下，γ是一个保核收缩且将¯Ω2中子集映射为C中有界子集，这说明定理1中条件3）成立。

下面说明定理1的条件2）成立。为此，假设存在x0∈C∩∂Ω2∩domL以及λ0∈（0，1）使得Lx0=λ0Nx0，即对t∈ ［0，1］有：

设t1∈ ［0，1］满足x0（t1）=R，有：

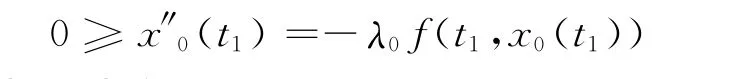
与条件H2）矛盾，所以定理1的条件2）成立。

下面证明条件4）成立。

对x∈KerL∩Ω2，有x（t）=c，t∈［0，1］，定义

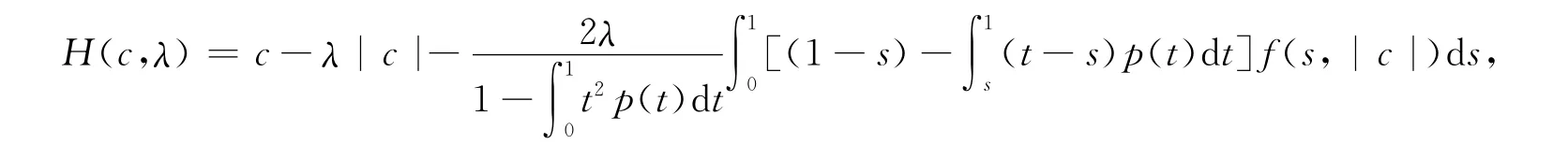
其中c∈［-R，R］，λ∈［0，1］。

假设H（c，λ）=0，则：

如果H（R，λ）=0，即

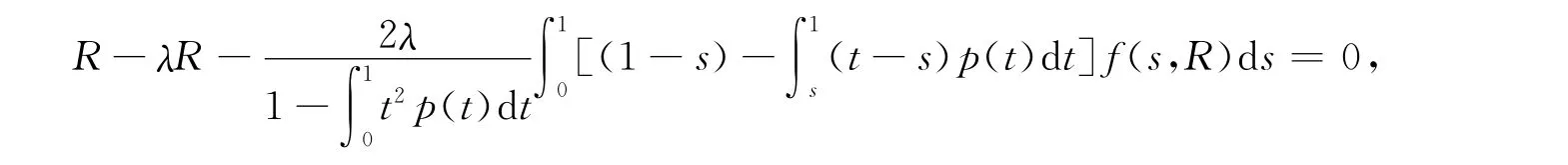
因此有：

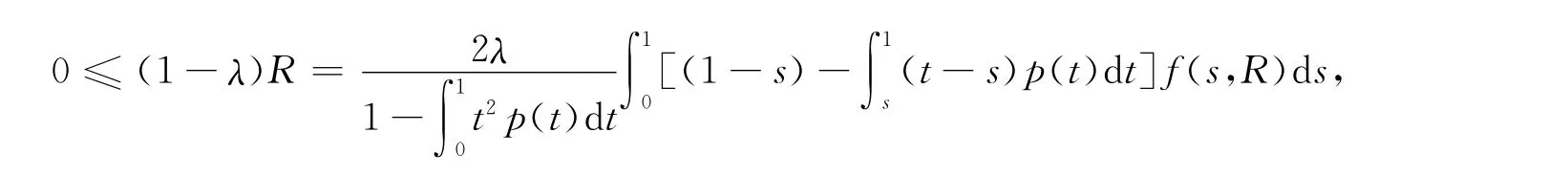
与条件H2）矛盾。

对x∈∂Ω2∩ KerL，λ∈ ［0，1］，有H（R，λ）≠0，因此有dB（H（c，0），KerL∩Ω2，0）=dB（H（c，1），KerL∩Ω2，0）。然而dB（H（c，0），KerL∩Ω2，0）=dB（I，KerL∩Ω2，0）=1。所以有：dB（［I-（P＋JQN）γ］|KerL，KerL∩Ω2，0）=dB（H（c，1），KerL∩Ω2，0）≠0。

对于x∈∂Ω2有：

因此定理1中条件6）成立。设x∈¯Ω2＼Ω1，t∈［0，1］，则有：

由条件H1）可得：

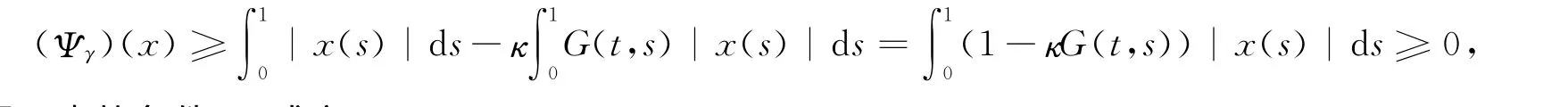
因此定理1中的条件7）成立。

最后，证明定理1中条件5）成立。

取u0（t）≡1，t∈ ［0，1］，显然有u0∈C＼｛0｝，C（u0）= ｛x∈C|x（t）＞0，t∈ ［0，1］｝。

取σ（u0）=1，设x∈C（u0）∩∂Ω1，有x（t）＞0，t∈ ［0，1］，0＜ ‖x‖ ≤r，x（t）≥M‖x‖，t∈ ［0，1］。

考虑到条件 H3），对所有x∈C（u0）∩∂Ω1，

所以对于x∈C（u0）∩∂Ω1，有‖x‖≤σ（u0）‖Ψx‖，即定理1中条件5）成立。由定理1可知，方程Lx=Nx在C∩（¯Ω2＼Ω1）中有1个解。

4 例 子

考虑如下共振边值问题：

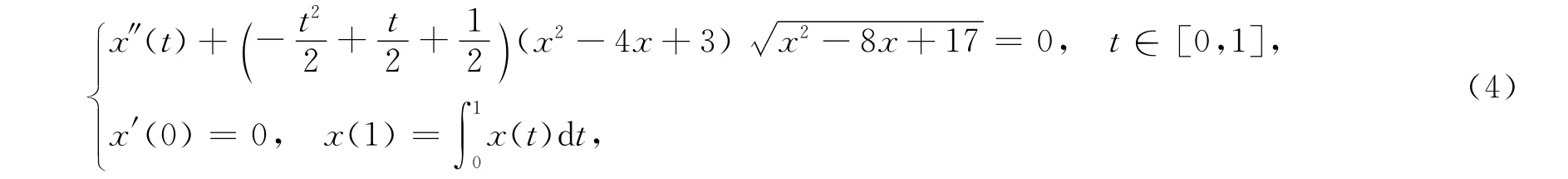
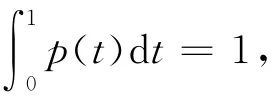
容易验证：

A2）f（t，R）＜0，对任意t∈ ［0，1］；

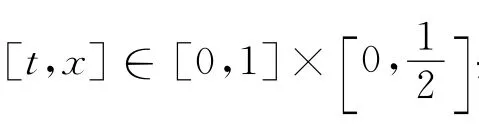
满足定理2的所有条件，因此，边值问题（4）在［0，1］上至少有1个正解。

［1］ BITSADZE A V，SAMARSKIĬA A.Some elementary generalizations of linear elliptic boundary value problems［J］.Doklal Akad Nauk SSSR，1969，185：739-742.

［2］ MOISEEV E I，IL’IN V A.Nonlocal boundary value problem of the second kind for a Sturm-Liouville operator［J］.Differential Equations，1987，23：979-987.

［3］ MA Ruyun.Positive solutions of a nonlinear three-point boundary value problem［J］.Electron Journal of Differential Equations，1999，34：1-8.

［4］ YANG Liu，LIU Xiping，JIA Mei.Multiplicity results for second-order m-point boundary value problem ［J］.Journal of Mathematical Analysis and Applications，2006，324（1）：532-542.

［5］ HAN Xiaoling.Positive solutions for a three-point boundary value problem at resonance［J］.Journal of Mathematical Analysis and Applications，2007，336（1）：556-568.

［6］ MA Ruyun.Multiplicity results for a three-point boundary value problem at resonance［J］.Nonlinear Analysis，2003，53（6）：777-789.

［7］ HENDERSON J.Double solutions of three-point boundary-value problems for second-order differential equations［J］.Electron Journal of Differential Equations，2004，115：1-7.

［8］ AGARWAL R P，O’REGAN D.Some new existence results for differential and integral equations［J］.Nonlinear Anal，1997，29（6）：679-692.

［9］ ZHANG Guowei，SUN Jingxian.Positive solutions of m-point boundary value problems［J］.Journal of Mathematical Analysis and Applications，2004，291（2）：406-418.

［10］江卫华，刘秀君，宗慧敏.具有共振的分数阶微分方程边值问题解的存在性［J］.河北科技大学学报，2014，35（6）：518-523.

JIANG Weihua，LIU Xiujun，ZONG Huimin.Existence of solutions for fractional differential equation boundary value problems at resonance［J］.Journal of Hebei University of Science and Technology，2014，35（6）：518-523.

［11］BAI Chuanzhi，FANG Jinxuan.Existence of positive solutions for three-point boundary value problems at resonance［J］.Journal of Mathematical Analysis and Applications，2004，291（2）：538-549.

［12］CREMINS C T.A fixed-point index and existence theorems for semilinear equations in cones［J］.Nonlinear Anal，2001，46：789-806.

［13］INFANTE G，ZIMA M.Positive solutions of multi-point boundary value problems at resonance［J］.Nonlinear Anal，2008，69：2458-2465.

［14］O’REGAN D，ZIMA M.Leggett-Williams norm-type theorems for coincidences［J］.Archlv der Mathematlk，2006，87（3）：233-244.

［15］MAWHIN J.Equivalence theorems for nonlinear operator equations and coincidence degree theory for mappings in locally convex topological vector spaces［J］.Differential Equations，1972，12：610-636.

［16］ZIMA M.Fixed point theorem of Leggett-Williams type and its application［J］.Journal of Mathematical Analysis and Applications，2004，299（1）：254-260.

［17］PETRYSHYN W V.On the solvability of in quasinormal cones with and k-set contractive［J］.Nonlinear Anal，1981，5（5）：585-591.