机床热误差建模技术研究进展

郭前建，王红梅，李爱军

（山东理工大学机械工程学院，山东淄博 255049）

1 热误差建模技术

随着对机床加工精度要求的日益提高，机床热变形对加工精度的影响越来越大。如图1所示，在精密加工中，机床热变形引起的加工误差即热误差占机床总误差的40%～70%。对热变形误差进行控制是提高机床加工精度的主要途径之一。

为减小热变形误差，提高机床加工精度，目前主要有两种方法：误差补偿法和误差防止法。误差防止法主要通过设计和制造途径来降低零部件的热变形，消除或减少可能的热源。例如，通过提高机床的设计和制造精度、采用严格的温度控制减小热源影响就属于误差防止。由于技术限制，应用误差防止法很难彻底消除热变形误差，且加工精度要求高于某一标准后，误差防止法的成本会按指数规律增加。热误差补偿法主要通过分析、统计、归纳掌握机床关键热源温度对热误差的影响规律，从而建立热误差模型，并利用模型计算结果去抵消热误差，原理如图2所示。由于能在机床上加工出超过机床本身精度的工件，热误差补偿已成为精密加工领域的主要技术之一。

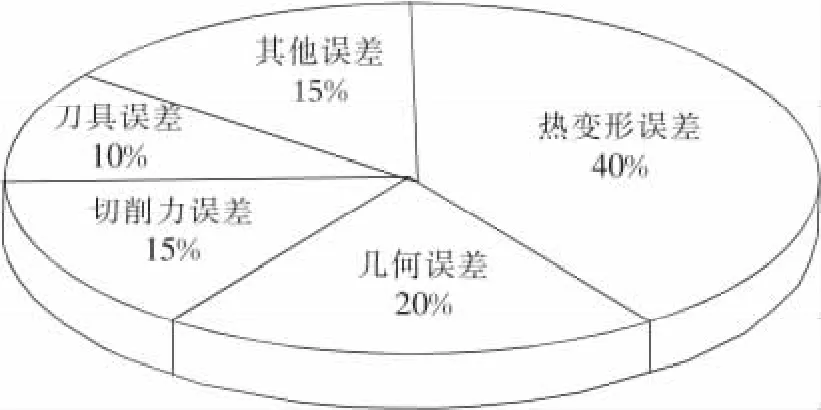
图1 各误差源所占比例Fig.1 Proportion of different error sources

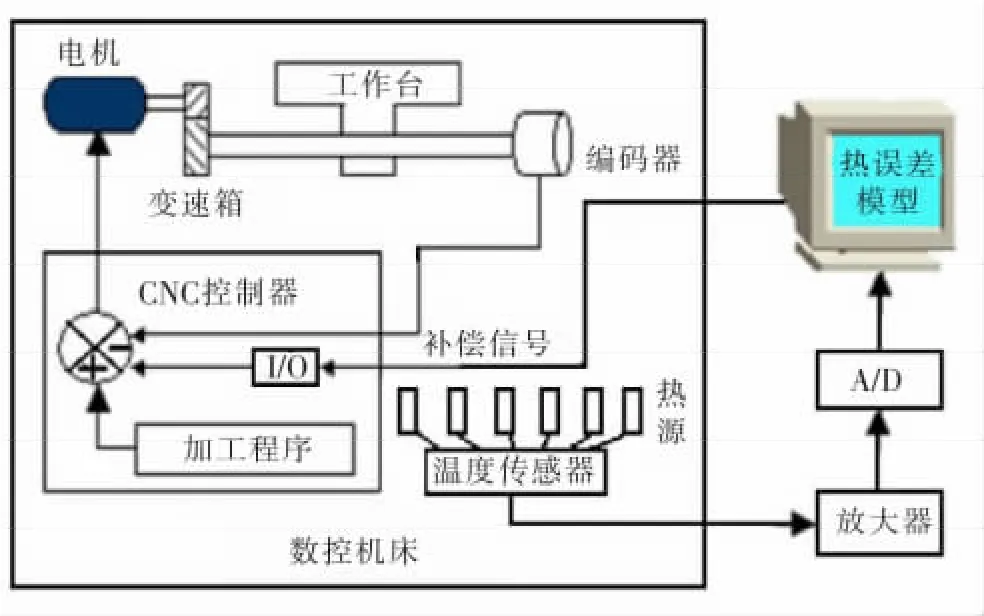
图2 热误差补偿技术的基本原理Fig.2 Basic principle of thermal error compensation technology

根据热误差补偿技术的基本原理，对机床实施热误差补偿的前提是能够对某一温度场下的热变形误差进行准确预报，然后根据预报值去抵消机床误差。这就要求尽可能准确地进行热误差建模，即建立机床热误差和温度变量之间的函数关系。

2 机床热误差建模技术研究现状

对于热误差建模的研究，国外在20世纪90年代就已经进行的如火如荼，其中最有影响力的当属美国密西根大学吴贤明制造研究中心的J.Ni团队。该团队的YANG等［1］早在1996年便将CMAC神经网络应用到了热误差建模中。1997年该团队的LIANG等［2］利用最小二乘法完成了1台加工中心的热误差建模，该模型在一机床生产厂家实现了商业化。1999年该团队的LO等［3］应用聚类算法实现了热误差的优化建模。除J.Ni团队外，还有其他一些研究团队和个人致力于热误差建模的研究，如加拿大麦克马斯特大学的SRIVASTAVA等［4］、韩国科学技术学院的YANG等［5］、美国密西根理工大学的 WANG等［6］及佛罗里达大学的MIZE等［7］。他们分别对BP神经网络、基于模糊ART-map的神经网络、灰色系统理论等在热误差建模中的应用进行了研究，并取得了一定的成果，遗憾的是他们的研究都没有得到延续。

进入21世纪，各国对精密加工技术的需求逐渐提高，热误差建模技术取得了更大的发展。2001年韩国庆北大学YANG团队的LEE完成了1台数控机床的热误差建模及补偿。LEE等［8］在热误差建模过程中提出了一种新的相关系数法，机床关键热源位置及热误差的确定主要依赖于各温度变量之间的相关系数。同年LEE等［9］还对一卧式加工中心实施了热误差补偿，实验过程中其应用模糊逻辑策略建立了该加工中心的热误差模型。

2002年LEE等［10］在上述研究基础上提出了一种新的建模方法，该方法通过连续回归分析获得最小剩余方差，用于建模过程中的变量选择。与此同时，韩国首尔国立大学的PAHK等［11］也对热误差建模技术进行了研究，并对多线性回归、神经网络、系统辨识3种热误差建模方法进行了比较，结果显示系统辨识建模方法的逼近误差最小。除几位韩国学者外，中国台湾省“国立中兴大学”的TSENG等［12］也在同期对热误差建模技术进行了深入研究，其利用多元线性回归方法、非线性指数回归方法分别建立了温度变量与热误差之间的数学模型。

2003年新加坡国立大学的RAMESH等［13-14］对热误差测量、建模及补偿技术进行了深入研究，他们认为加工要求对关键热源的温度具有重要影响，因此在一三轴立式加工中心上针对不同加工要求做了大量实验，获得了大量测量数据，最后根据测量结果分析不同加工条件对热误差的影响，最后，RAMESH等利用获得的实验数据对该立式加工中心的热误差进行了建模。建模过程中，他们充分考虑不同加工要求对热误差的影响，利用基于规则系统的贝叶斯网络模型对获得的测量数据进行分类，然后应用支持向量机（SVM）模型预测热误差。RAMESH等的研究充分考虑了加工要求对热误差的影响，在模型鲁棒性方面取得了很大进展。与此同时，加拿大麦克马斯特大学的HARRIS等［15］在SRIVATAVA等的研究基础上，对一坐标测量机的热误差建模及补偿技术进行研究，经过补偿热误差减小了65%～90%。同年，韩国首尔国立大学的LEE等［16］公布了自己的最新研究成果，在选择温度变量时他首次应用了独立成分分析方法，实现了温度变量的初选，初选完成后进一步应用最优脑外科算法减少了温度变量，最终应用优选的温度变量建立了MCH-10机床的热误差模型。

2005年以来，针对热误差建模的研究越来越多，除美国、韩国、新加坡、加拿大及中国台湾省的学者外，德国、西班牙等科技强国也出现了一些学者对热误差建模进行研究。2005年美国Delphi公司的YANG等［17-18］在J.Ni团队多年研究的基础上，针对不同加工条件对热误差模型的影响进行重点研究，分两部分在International Journal of Machine Tools &Manufacture上公布了自己的研究成果。在第Ⅰ部分的研究中，YANG等提出了一种可随加工条件变化自动更新热误差模型的系统模型自适应方法，并在一三轴数控加工中心上进行了实验。在第Ⅱ部分的研究中YANG等提出了一种新的动态神经网络建模方法，该方法用动态神经网络跟踪非线性的、动态的机床误差。为满足机床加工的非稳态要求，YANG等将集成反馈神经网络引入热误差建模。实验结果表明集成反馈神经网络在模型鲁棒性方面优于多变量回归分析法、多层前向神经网络、反馈神经网络等。

2006年WANG等［19］提出了一个新概念——通过显示机床热状态控制机床热效应，并引入潜在变量建模方法来解决系统辨识理论难以克服的问题。另外，中国台湾省“中原大学”的KANG团队［20］也在2006年公布了自己的研究成果，他们提出了一种新的热误差建模方法，该方法将前向神经网络与包含线性回归、移动平均、自动回归在内的混合滤波器组合在一起，以提高热误差模型的预测精度、缩减热误差模型的计算时间。2008年西班牙萨拉戈萨大学的SANTOLARIA等［21］对一关节臂式坐标测量机的热误差建模进行了研究，并建立了一个新的经验修正模型，经过误差修正关节臂的运动精度有了较大提高。2009年美国Microlution公司的CREIGHTON等［22］对一微型高速铣床的主轴热误差进行了分析，通过对主轴热变形误差及主轴的不同位置进行温度测量获得相关实验数据，然后根据实验数据建立热误差模型，该模型具有指数形式。

中国大陆对热误差建模技术的研究还相对落后，并且主要集中在近几年。尽管已有很多专家、学者在这一领域展开了工作，但主要是一些研究个人，很少有研究团队。在这些科研团队中，最有影响的当属上海交通大学的杨建国团队，杨建国教授从20世纪90年代开始就已致力于热误差建模的研究，其博士学位论文“数控机床误差综合补偿技术及应用”被评为中国优秀博士学位论文。近年来该团队一直从事热误差建模领域的研究工作，取得了可喜的成果。2002年该团队的DU等［23］提出了一种新的正交回归建模法，建模过程综合考虑了机床结构、环境因素、工程判断及相关经验的影响。2005年YANG等［24］应用多元线性回归方法建立了1台INDEX-G200加工中心的热误差模型，模型经过变量优选后非常简单，且具有较高的逼近精度。同年，杨建国等［25］应用多元回归最小二乘法建立了某数控机床主轴的径向热误差模型，应用该模型后主轴径向误差降低了约55%。该团队的李永祥等［26］则分别对神经网络及灰色系统模型在热误差建模中的应用进行了研究。与此同时，天津大学章青教授团队的岳红新等［27］则基于多体系统理论，建立了某四轴加工中心的综合误差模型，并运用RBF神经网络对热误差模型进行参数辨识。另外新疆大学的穆塔里夫·阿赫迈德教授团队也公布了自己在热误差建模领域的研究成果，包括满蛟等［28］的偏最小二乘回归法、王新的基于主成分分析法的多元线性回归法。

2006年杨建国团队的LI等［29］在前面的研究基础上又提出了3种新的热误差建模方法，即时序分析法、基于灰色系统理论的建模方法及将灰色系统理论与时序分析法结合在一起的智能混合预测方法。同年，该团队的沈金华等［30］分别对人工神经网络及聚类回归算法在热误差建模中的应用进行了研究，ZHAO等［31］则借助有限元分析及多元线性回归方法建立了某数控机床的热误差模型。除杨建国团队外，广西工学院的吴汉夫［32］、西安交通大学的卢秉恒教授团队（结合因子分析法及多元线性回归方法建立了某高精度压印机的热误差模型［33］）也在同期开展了热误差建模研究。2007年杨建国团队的闫嘉钰等［34］又提出了一种新的热误差建模方法，该方法结合灰色综合关联度与最小二乘法，建立了某数控车削中心的热误差模型。同年上海交通大学的王智明等［35］对多项式回归理论在热误差建模中的应用进行了研究，并利用多项式回归理论中的增广样本相关系数，结合复相关系数的方法剔除与因变量和其他自变量相关系数均很低的自变量，建立了机床热误差模型。

2008年杨建国团队的WU等［36］又提出了2种新的建模方法，其中一种将BP神经网络与遗传算法相结合，而另一种则将BP神经网络与PSO算法相结合，应用2种优化算法建立的热误差模型最终都在精密车削中心上得到了应用。同时该团队的闫嘉钰等［37］在李永祥博士的研究基础上应用灰色系统理论建立了某CNC机床的GM（1，4）及GM（0，4）模型，结果表明两种新模型同传统GM（1，1）模型相比可获得更高的预测精度。同年，重庆大学的张根保教授团队则将热误差建模的研究对象由传统的车铣加工中心扩展到了新研发的零传动滚齿机上［38］。另外，浙江大学的傅建中团队也在同期公布了自己的研究成果，团队的林伟青等［39］分别建立了基于在线最小二乘支持向量机和基于LS-SVM与遗传算法的热误差模型，团队的吴雄彪则建立了基于贝叶斯网络的热误差模型。

2009年杨建国团队的闫嘉钰等［40］又提出了2种新的建模方法。第1种方法通过线性和的方式对基于不同数学理论所建立的热误差模型进行综合，并以不同拓扑结构及训练算法的反向传播神经网络为例，建立了最优线性组合神经网络。第2种方法针对现有误差预测模型无法实现结构自适应调整和在线训练不足的问题，通过对比人体免疫系统和人工神经网络，提出人工免疫RBF（AIRBF）网络，实现了网络结构的动态调整和在线学习。同年，该团队的张宏韬等［41］应用径向基（RBF）神经网络模型的学习性能，对一台数控加工中心的主轴温度与主轴径向热误差关系进行了在线建模研究。与此同时，浙江大学的林伟青等［42］又提出了一种基于动态自适应加权最小二乘支持矢量机的热误差建模方法，该方法运用动态自适应算法，优化选择建模过程中的参数，并对采样数据进行初始最小二乘支持矢量机建模，然后根据误差变量确定权重系数，得到基于加权最小二乘支持矢量机的热误差模型。另外，南京航空航天大学的郑学刚等［43］则在同期提出了一种基于模糊神经网络的热误差建模方法，该方法将模糊逻辑理论和神经网络相结合，提高了网络的泛化能力。

通过对上述不同热误差建模方法的研究现状进行总结，可以看到几种典型建模方法各有优缺点，具体如表1所示。预测精度方面，各种仿生智能预测模型具有先天优势，相比之下回归模型的预测能力较弱。模型可见性方面，回归模型由于所有参数可见，易于对其进行控制，而神经网络模型由于其“黑箱”特性，可见性最差。在模型的鲁棒性方面，各种智能预测模型同样具有不可比拟的优势，而回归模型由于模型参数不能实时修正，实时性最差。在模型计算能力方面，回归模型由于模型简单，计算效率最高，实时性最强，而各种智能仿生模型由于算法过于复杂，实时性一般较差。

表1 各种热误差模型的性能比较Tab.1 Performance comparison of different thermal error models

3 研究展望

纵观国内外，热误差建模技术从20世纪90年代开始就已成为研究热点。近10年来，随着研究的逐步深入及涉足该领域的专家、学者越来越多，取得的科研成果也越来越多，目前出现了如下发展动态。

1）各种热误差模型如多元回归模型、神经网络模型、多体系统理论模型、灰色关联模型等，都通过建立温度变量与热误差之间的函数关系式，从而实现了对机床热误差的有效预测，然而绝大多数研究人员建立的热误差模型都是固定不变的，只有个别学者如YANG等针对热误差动态建模展开了研究，遗憾的是模型的改变仅限于已预先确定的温度变量的范围之内，而与预先确定的温度变量之外的其他热源温度无关。也就是说在建立热误差模型之前，所需的温度变量就已通过各种方法确定，一旦确定了建模所需温度变量，其他热源温度对热误差的影响将被排除在外。一般来说，应用选定的温度变量进行建模完全可以满足要求，但选定的变量组合是否是最优变量组合很难评定，而且机床在不同使用阶段是否应选用不同变量组合来建模也值得商榷。随着各国对机床加工精度的要求越来越高，如何提高热误差模型的精度，并对建立的模型进行优化评估，已成为科研人员亟待解决的一个问题。

为提高模型逼近能力，并对所建模型进行优化，各种先进的智能算法和仿生优化算法仍然是科研人员的首选［44-45］，例如改进粒子群优化算法、蚁群算法、多传感器信息融合、模糊神经网络、投影追踪回归算法等等。

2）所建热误差模型主要是针对机床某一坐标轴的，很少有模型综合考虑了热变形误差对机床多个坐标轴的影响，这与目前日渐广泛的五轴机床应用是不相符的，严重影响了热误差建模技术在数控机床上的实际应用。为了综合考虑热变形对机床误差的全面影响，建立能够反映机床各轴热变形的综合误差模型已势在必行。

3）所建热误差模型主要针对确定的机床类型、确定的加工条件、确定的加工状态，一旦机床类型、加工条件、加工状态等发生变化，模型的逼近能力将大打折扣，所建模型的可移植能力太差。为了尽量提高所建热误差模型的鲁棒性，综合考虑各种因素影响，建立能够反映不同机床类型、不同加工条件及不同加工状态的热误差模型是该领域又一个亟待解决的问题。

［1］ YANG S，YUAN J，NI J.The improvement of thermal error modeling and compensation on machine tools by CMAC neural network［J］.International Journal of Machine Tools and Manufacture，1996，36（4）：527-537.

［2］ LIANG J，LI H F，YUAN J X，et al.A comprehensive error compensation system for correcting geometric，thermal，and cutting forceinduced errors［J］.International Journal of Advanced Manufacturing Technology，1997，13（10）：708-712.

［3］ LO C H，YUAN J，NI J.Optimal temperature variable selection by grouping approach for thermal error modeling and compensation［J］.International Journal of Machine Tools and Manufacture，1999，39（9）：1383-1396.

［4］ SRIVASTAVA A K，VELDHUIS S C，ELBESTAWIT M A.Modeling geometric and thermal errors in a five-axis CNC machine tools［J］.International Journal of Machine Tools and Manufacture，1995，35（9）：1321-1337.

［5］ YANG M，LEE J.Measurement and prediction of thermal errors of a CNC machining center using two spherical balls［J］.Journal of Materials Processing Technology，1998，75（1／2／3）：180-189.

［6］ WANG Y，ZHANG G，MOON K S.Compensation for thermal error of a multi-axis machining center［J］.Journal of Materials Processing Technology，1998，75（1／2／3）：45-53.

［7］ MIZE C D，ZIEGERT J C.Neural network thermal error compensation of of a machining center［J］.Journal of International Societies for Precision Engineering and Nanotechnology，2000，24（4）：338-346.

［8］ LEE J H，YANG S H.Fault diagnosis and recovery for a CNC machine tool thermal error compensation system［J］.Journal of Manufacturing System，2001，19（6）：428-434.

［9］ LEE J H，YANG S H.Thermal error modeling of a horizontal machining center using fuzzy logic strategy［J］.Journal of Manufacturing System，2001，3（2）：120-127.

［10］LEE J H，YANG S H.Statistical optimization and assessment of a thermal error model for CNC machine tools［J］.International Journal of Machine Tools and Manufacture，2002，42（1）：147-155.

［11］PAHK H J，LEE S W.Thermal error measurement and real time compensation system for the incorporating the spindle thermal error and feed axis thermal error［J］.International Journal of Advanced Manufacturing Technology，2002，20（7）：487-494.

［12］TSENG P C，HO J H.A study of high-precision lathe thermal errors and compensation［J］.International Journal of Advanced Manufacturing Technology，2002，19（11）：850-858.

［13］RAMESH R，MANNAN M A，POO A N.Thermal errors measurement and modeling in machine tools.PartⅠ：Influence of varying operating conditions［J］.International Journal of Machine Tools and Manufacture，2003，43（4）：391-404.

［14］RAMESH R，MANNAN M A，POO A N.Thermal errors measurement and modeling in machine tools.PartⅡ：Hybrid Bayesian Network—support vector machine model［J］.International Journal of Machine Tools and Manufacture，2003，43（4）：405-419.

［15］HARRIS J O，SPENCE A D.Geometric and quasi-static thermal error compensation for a laser digitizer equipped coordinate measuring machine［J］.International Journal of Machine Tools and Manufacture，2004，44（1）：65-77.

［16］LEE D S，CHOI J Y.ICA based thermal source extraction and thermal distortion compensation method for a machine tool［J］.International Journal of Machine Tools and Manufacture，2003，43（6）：589-597.

［17］YANG H，NI J.Adaptive model estimation of machine tool thermal error based on recursive dynamic modeling strategy［J］.International Journal of Machine Tools and Manufacture，2005，45（1）：1-11.

［18］YANG H，NI J.Dynamic neural network modeling for nonlinear，nonstationary machine tool thermally induced error［J］.International Journal of Machine Tools and Manufacture，2005，45（4／5）：455-465.

［19］WANG H，HUANG Q，YANG H.In-line statistical monitoring of machine tool thermal error through latent variable modeling［J］.Journal of Manufacturing System，2006，25（4）：279-292.

［20］KANG Y，CHANG C W，HUANG Y，et al.Modification of a neural network utilizing hybrid filters for the compensation of thermal deformation in machine tools［J］.International Journal of Machine Tools and Manufacture，2007，47（2）：376-387.

［21］SANTOLARIA J，YAGUE J，JIMENEZ R.Calibration-basded thermal error model for articulated arm coordinate measuring machines［J］.Precision Engineering，2009，33（4）：476-485.

［22］CREIGHTON E，HONEGGER A，TULSIAN A，et al.Analysis of thermal errors in a high-speed micro-milling spindle［J］.International Journal of Machine Tools and Manufacture，2010，50（4）：386-393.

［23］DU Z C，YANG J G，YAO Z Q，et al.Modeling approach of regression orthogonal experiment design for the thermal error compensation of a CNC turning center［J］.Journal of Materials Processing Technology，2002，129（1／2／3）：619-623.

［24］YANG J G，REN Y Q，LIU G L.Testing，variable selecting and modeling of thermal errors on an INDEX-G200turning center［J］.International Journal of Advanced Manufacturing Technology，2005，26（7／8）：814-818.

［25］杨建国，张宏韬，童恒超，等.数控机床热误差实时补偿应用［J］.上海交通大学学报，2005，39（9）：1389-1392.

YANG Jianguo，ZHANG Hongtao，TONG Hengchao，et al.The application of real-time thermal error compensation on NC machine tools［J］.Journal of Shanghai Jiaotong University，2005，39（9）：1389-1392.

［26］李永祥，杨建国.灰色系统模型在机床热误差建模中的应用［J］.中国机械工程，2006，17（23）：2439-2442.

LI Yongxiang，YANG Jianguo.Application of grey system model to thermal error modeling on machine tools［J］.China Mechanical Engineering，2006，17（23）：2439-2442.

［27］岳红新，章青，王慧清.基于多体理论的加工中心热误差建模及补偿技术研究［J］.组合机床与自动化加工技术，2005（1）：27-29.

YUE Hongxin，ZHANG Qing，WANG Huiqing.The research on the thermal error model and compensation technique in machining centers based on MBS［J］.Modular Machine Tool &Automatic Manufacturing Technique，2005（1）：27-29.

［28］满蛟，王新，穆塔里夫·阿赫迈德，等.利用偏最小二乘回归法对主轴热误差数值建模的研究［J］.组合机床与自动化加工技术，2005 （11）：17-19.

MAN Jiao，WANG Xin，MUTELLIP Ahmat，et al.Numerical modeling research for thermal error for the spindle by partial least-squares regression method［J］.Modular Machine Tool &Automatic Manufacturing Technique，2005 （11）：17-19.

［29］LI Y X，YANG J G，ZHANG H T.Application of grey system model to thermal error modeling on machine tools［J］.International Federation for Information Processing（IFIP），2006，207：511-518.

［30］沈金华，赵海涛，杨建国，等.数控机床热补偿中温度变量的选择与建模［J］.上海交通大学学报，2006，40（2）：181-184.

SHEN Jinhua，ZHAO Haitao，YANG Jianguo，et al.The selection and modeling of temperature variables for the thermal error compensation on machine tools［J］.Journal of Shanghai Jiaotong University，2006，40（2）：181-184.

［31］ZHAO H T，YANG J G，SHEN J H.Simulation of thermal behavior of a CNC machine tool spindle［J］.International Journal of Machine Tools and Manufacture，2007，47：1003-1010.

［32］吴汉夫.三轴加工中心热误差推定的建模方法［J］.广西工学院学报，2006，17（4）：47-49.

WU Hanfu.Modeling on estimation of thermal error of 3axes machining center［J］.Journal of Guangxi University of Technology，2006，17（4）：47-49.

［33］严乐，刘红忠，卢秉恒，等.高精度压印机热误差补偿中温度变量的辨识［J］.西安交通大学学报，2006，40（7）：827-830.

YAN Le，LIU Hongzhong，LU Bingheng，et al.Temperature variable recognition for thermal error compensation in high precision imprint［J］.Journal of Xi’an Jiaotong University，2006，40（7）：827-830.

［34］闫嘉钰，张宏韬，杨建国，等.基于灰色综合关联度的数控机床热误差测点优化新方法及应用［J］.四川大学学报（工程科学版），2008，40（2）：160-164.

YAN Jiayu，ZHANG Hongtao，YANG Jianguo，et al.Application of a new optimizing method for the measuring points of CNC machine thermal error based on grey synthetic degree of association［J］.Journal of Sichuan University（Engineering Science Edition），2008，40（2）：160-164.

［35］王智明，彭安华，王其兵.多项式回归理论在机床热误差建模中的应用［J］.兰州理工大学学报，2007，33（6）：40-42.

WANG Zhiming，PENG Anhua，WANG Qibing.Application of polynomial regression theory in thermal error modeling of machine tool［J］.Journal of Lanzhou University of Technology，2007，33（6）：40-42.

［36］WU H，ZHANG H T，GUO Q J，et al.Thermal error optimization modeling and real-time compensation on a CNC turning center［J］.Journal of Materials Processing Technology，2008，207：172-179.

［37］闫嘉钰，杨建国.灰色GM（X，N）模型在数控机床热误差建模中的应用［J］.中国机械工程，2009，20（11）：1297-1299.

YAN Jiayu，YANG Jianguo.Application of grey GM（X，N）model on CNC machine thermal modeling［J］.China Mechanical Engineering，2009，20（11）：1297-1299.

［38］张新玉，张根保，黄强，等.零传动滚齿机几何误差和热误差综合建模［J］.机械设计，2008，25（3）：40-43.

ZHANG Xinyu，ZHANG Genbao，HUANG Qiang，et al.Synthetical modeling on geometric error and thermal error of direct-drive hobbing machines［J］.Journal of Machine Design，2008，25（3）：40-43.

［39］林伟青，傅建中，许亚洲，等.基于LS-SVM与遗传算法的数控机床热误差辨识温度传感器优化策略［J］.光学精密工程，2008，16（9）：1682-1686.

LIN Weiqing，FU Jianzhong，XU Yazhou，et al.Optimal sensor placement for thermal error identification of NC machine tool based on LS-SVM and genetic algorithm［J］.Optics and Precision Engineering，2008，16（9）：1682-1686.

［40］闫嘉钰，杨建国.基于人体免疫系统RBF网络的数控机床热误差建模［J］.上海交通大学学报，2009，43（1）：148-152.

YAN Jiayu，YANG Jianguo.Immune system based RBF neural network modeling for machine tool thermal error［J］.Journal of Shanghai Jiaotong University，2009，43（1）：148-152.

［41］张宏韬，杨建国.RBF网络在线建模方法在热误差实时补偿技术中的应用［J］.上海交通大学学报，2009，43（5）：807-810.

ZHANG Hongtao，YANG Jianguo.Application of online modeling method based on RBF network in real-time thermal error compensation［J］.Journal of Shanghai Jiaotong University，2009，43（5）：807-810.

［42］林伟青，傅建中，许亚洲，等.数控机床热误差的动态自适应加权最小二乘支持矢量机建模方法［J］.机械工程学报，2009，45（3）：178-182.

LIN Weiqing，FU Jianzhong，XU Yazhou，et al.Modeling of NC machine tool thermal error based on adaptive best-fitting WLS-SVM［J］.Journal of Mechanical Engineering，2009，45（3）：178-182.

［43］郑学刚，赵宇，吴洪涛.机床热误差建模及检测系统模块设计［J］.电子测量与仪器学报，2009，23（9）：74-78.

ZHENG Xuegang，ZHAO Yu，WU Hongtao.Thermal error modeling and detection system module design in machine tools［J］.Journal of Electronic Measurement and Instrument，2009，23（9）：74-78.

［44］许博，杨慧中.软测量建模中的数据校正［J］.河北科技大学学报，2012，33（6）：510-513.

XU Bo，YANG Huizhong.Data collection in soft sensor modeling［J］.Journal of Hebei University of Science and Technology，2012，33（6）：510-513.

［45］李冬梅，陈军霞.聚类分析法在公交网络评价中的应用［J］.河北科技大学学报，2012，33（3）：279-282.

LI Dongmei，CHEN Junxia.Application of cluster analysis in evaluation of public traffic network［J］.Journal of Hebei University of Science and Technology，2012，33（3）：279-282.