基于标准偏差的Bessel公式的证明

邵建新

（石河子大学 师范学院,新疆 石河子 832003）

0 引言

在测量误差、测量不确定度及数据处理的文献中，都无一例外地会给出Bessel公式。但仔细研究会发现如下问题：一是有关量（参数）的符号表示混乱，使得本就公理化体系不够严密的误差理论或不确定度理论从源头上产生迷雾；二是Bessel公式数学表述不统一；三是经典的证明方法或多或少存在一些不足；四是公式的适用范围众说不一。笔者认为产生这些问题的根本原因是由于对核心概念—标准偏差的定义和意义没有完全认清的缘故。本文先将有关量（参数）的符号表示统一起来，然后分析讨论两类经典证明方法存在的不足，在给出各种标准偏差的定义且阐明其意义的基础上，对经典证法进行改进，并提出一种新的Bessel公式的证明方法，最后讨论Bessel公式的适用范围，这对完整准确地理解和应用Bessel公式具有很好的指导意义。

1 有关量符号表示的统一

为了分析、研究、解决问题方便，有关量的符号表示应当兼顾理论研究与实际应用的需要。建议符号表示采用下述规定：大写英文字母表示随机变量总体，小写英文字母表示随机变量可能的取值。如X、Y等表示随机变量总体，x、y(可带有下标如xi、yi)表示随机变量可能的取值表示随机变量总体的均值，“”表示随机变量总体均值的取值。样本测得值（又称观测值、观察值）也用小写英文字母表示。

在参数估计中，除了用大写的希腊字母表示统计量外，也常用小写的希腊字母表示统计量如θ、μ等。有时，这种情况下其估计量用表示，其估计值用表示。

上述规定的核心可以概括为：大写字母表示“量”，小写字母表示“值”。

由于相关量（参数）的符号表示混乱及对各种标准偏差的意义认识不清等原因，造成Bessel公式的数学表达式有多种形式，并由此带来不必要的麻烦。

2 Bessel公式经典证法的讨论

2.1 三类经典证法

文献[1-6]给出的Bessel公式的证法可作为第一类经典证法的代表。这类证法对概率论和数理统计的知识要求较高。为避开概率论与数理统计知识的束缚，文献[7-10]给出的Bessel公式的证法可作为第二类经典证法的代表。其突出特征是利用下面的等式

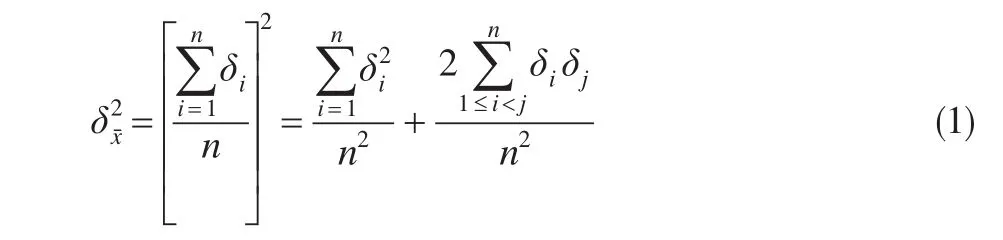
（δi=xi-μ 称为测得值 xi的误差，称为算术平均值的误差，μ为被测量的真值）

为了得出等式

证明Bessel公式，需要利用当n充分大时，有

成立。文献[7-10]对式（3）的证明只是简单的一笔带过，认为当n充分大时，式（3）一定成立，理由是δi很小，随机误差满足正态分布。

文献[11]给出的证法可作为第三类经典证法的代表，其突出特征是将误差看作随机变量，并假定随机误差服从正态分布。

2.2 一些文献对经典证法提出的质疑

文献[12-15]对第二类证法提出了质疑，认为当n充分大时式（3）并不成立。理由是当式（3）成立时，由式（1）一定可以得到：

2.3 笔者的观点

在第二类证法中，当n充分大时，式（3）及式（4）都是成立的。因为误差理论中是将随机误差看作无穷小量处理的，而两个无穷小量的乘积是无穷小量，有限个无穷小量的和仍然是无穷小量。若δi是无穷小量，则是δi的高阶无穷小量。

至于第三类证法，假定测量数据服从正态分布也是不合理的，因为Bessel公式的成立并不需要正态分布这一条件。

为了便于分析论证，有必要先给出各种标准偏差的定义，并阐明其意义。我们的方法是：先建立理想模型（数学模型），其次考虑测量实际，然后建立理想模型与实际测量之间的逻辑联系。

3 各种标准偏差的定义及其意义

3.1 总体标准偏差

3.1.1 总体标准偏差的定义

在计量学中,总体是指对被测量X在测量重复性条件下或复现性条件下无限多次测得值的集合：

这是一个无穷集合。其数据的分散性用标准偏差（简称标准差）σ来描述,定义成：

众所周知，方差σ2反映了测得值的分散程度，但由于方差的量纲是被测量的平方，使用起来不直观，也不方便，因此引入标准偏差（简称标准差）σ这个量。

3.1.2 总体标准偏差σ的意义

（1）σ是总体内所有的无穷多个测得值与真值之差的方和均值的正平方根（又说成是总体方差的正平方根,物理学上称之为方均根值）,它是从总体上描述各测得值xi相对于被测量真值μ的平均分散程度的一个参数。因而σ称为总体的标准偏差。σ值小,表明平均来讲测得值相对于被测量真值μ比较集中；σ值大,表明平均来讲测得值相对于被测量真值μ比较分散。

（2）σ仅具有理论意义。σ的表达式中含有被测量的真值μ,而真值通常是不能确知的；而且测量次数n也不可能是无穷多次,因此σ是一个不能确知的参数（即便是某些个别情况下知道真值,或采用约定真值,也不能确知，因为测量次数不可能做到无穷多次）。

（3）σ的实质是针对真值可以确知且测量次数可以为无穷多次的理想情况下，反映各测得值相对于被测量真值μ的平均分散程度分散的一个特征参数。既然σ表征的是平均分散程度,那就意味着测得值集合即总体内任何一个单次测得值xi的分散性都是σ。故又称σ是单次测得值xi的测量标准偏差,所以有时也将σ写作σ(xi)。但需要特别注意的是,将σ称作单次测得值xi的标准偏差,容易造成仅有xi时,仍有σ(xi)的错误认识。实际上,这里谈到的σ(xi)是基于式（5）中的所有测得值,离开了除xi的其它测得值,谈σ(xi)就没有意义了。

3.2 实验标准偏差

3.2.1 实验标准偏差的定义

由于任何实际的测量,重复测量的次数n总是有限的,因此式（6）给出的是个理想模型,实际中无法求出σ。设在重复性或复现性条件下,对被测量进行有限的n次独立重复观测,获得测得值集合：

显然,式（8）是个有限集合。如果测量仅仅存在随机性误差,则相应的算术平均值是被测量真值μ的最佳估计值：

由于各种影响量的随机变化或随机效应时空影响的不同,导致各次测得值xi不尽相同,也即数据存在分散性。其分散性用实验标准偏差s(xi)（简称实验标准差）来描述,定义成：

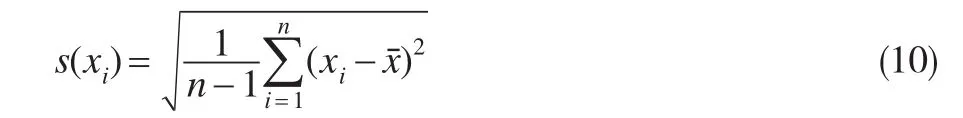
式（11）就是著名的Bessel公式。

当然，式（8）中各测得值的分散性是个客观存在的事实，描述其分散性的实验标准偏差s(xi)的计算式不止Bessel公式一种。还有极差法、最大似然法、彼得斯公式法、最大误差法、最大残差法、最大方差法、最大类间方差法、联合方差法、闭合差法和最小二乘法等等。但Bessel公式法最为基本、最为常用。

3.2.2 实验标准偏差的意义

（1）s(xi)是测得值集合的标准偏差（又称样本标准偏差）。s(xi)反映的是式（8）这个测得值集合中所有的n个测得值相对于样本均值（算术平均值、最佳估计值）的分散性,它是从整体上描述各测得值xi相对于的平均分散程度的一个参数,因此s(xi)通常也写成s。（s2(xi)常写成s2）。

（2）s(xi)的实质是表示测得值集合中各测得值相对于样本均值（算术平均值、最佳估计值）的平均分散程度。既然是平均分散程度,那就表明测得值集合即式（8）内任何一个单次测得值xi的分散性都是s(xi)，故又称s(xi)是单次测得值xi的实验标准偏差。但这种说法容易造成仅有xi时,仍有s(xi)的错误认识。实际上,这里谈到的s(xi)是基于式（8）中的n个测得值,离开了除xi的其它测得值,谈s(xi)就没有意义了。

（3）实验标准差s(xi)是总体标准差σ(xi)的有偏估计（s2(xi)是总体方差σ2的无偏估计）。为了使估计更可靠,应尽可能增加测量次数n。因为贝塞尔公式（11）成立的条件是n充分大。

如果被测量的估计值不随时间发生变化,则有：

即实验标准偏差s(xi)的期望值是σ(xi)。

（4）s(xi)是规定条件下特定测量系统的固有特性。在明确了被测量、测量方法、测量程序等规范化的常规测量中,s(xi)是该规定条件下的一个特定测量系统的固有特性,也是该特定测量系统的一项技术指标,即它是表征测得值之间分散性的指标。这里,测量系统的含义是指“将一台或多台测量仪器与其他器具（包括任何试剂和电源）组装起来,适用于在特定种类的量的规定区间内给出测得值的全套装置”。并且,由本文提供的新证法可以看出,由式（11）计算出的实验标准差与数据的分布规律无关。

3.3 平均值的实验标准偏差

3.3.1 为什么要引入平均值的实验标准偏差

由上文的讨论可知,s(xi)是表征在规定条件下的一个特定测量系统测得值分散性的参数,通常并不是用来描述测得值分散性的参数（当然,如果在众多的测得值中取某个值xi作为测量结果这种情况除外）。因为在通常的重复测量中,我们是用多次测得值的算术平均值作为测量结果的。显然,s(xi)无法描述的分散性,故需要引入描述算术平均值分散性的参数—平均值实验标准偏差。

3.3.2 平均值的实验标准偏差的定义

算术平均值是个随机变量。如果在相同的条件下对同一被测量值作多组重复的系列测量,则每一系列测量都存在一个算术平均值由于随机误差的存在,各个测量列的算术平均值也不相同,它们围绕算术平均值的数学期望值—a有一定的分散性。这种分散性可用相应的标准偏差——平均值实验标准差s(来描述。基于Bessel公式给出实验标准偏差的定义方法不难给出s()的定义：

设对被测量X作n组重复的系列测量,每组测量对应的算术平均值是（i=1,2,...,n）则各构成集合：

3.3.3 平均值实验标准偏差的意义

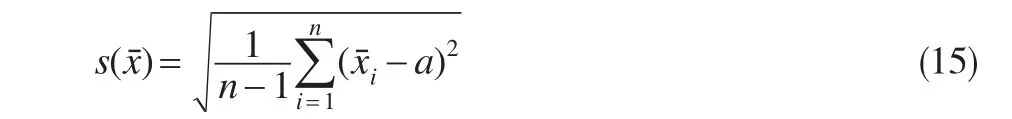
由于式（15）中含有算术平均值的数学期望值,实际上难以用它求出s()。而且,对于通常的测量一般并不实施对被测量进行多组重复测量的操作（除非有特殊需要）。为此必须寻求s()另外的计算公式。

对式（9）两边取方差,可得：

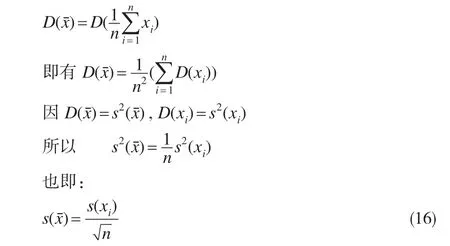
为给出基于标准偏差意义证明Bessel公式的新方法，还需给出总体均值的标准偏差σ(*)。

3.4 总体均值的标准偏差

3.4.1 总体均值的定义

由于误差普遍存在，为了提高测量精度，理论上是将式（1）中的算术平均值—总体均值作为测量结果，因此总体均值(即被测量X的数学期望)定义如下：

显然，式（17）定义的总体均值只具有理论意义，实际测量时无法实现。这里用*表示总体均值，是为了和测量列（样本）的均值相区别。

3.4.2 总体均值的标准偏差的定义

参照平均值实验标准偏差的定义方法不难给出总体均值的标准偏差的定义。

设在相同条件下对被测量作无穷多组重复的系列测量,每组测量的算术平均值是（i=1,2,...,∞）则总体均值的标准偏差为：

3.4.3 总体均值标准偏差的意义

显然，总体均值标准偏差仍然只有理论意义。因为这里不仅涉及到真值，每个测量列中还要求测量次数无穷多，而且测量列的组数也是无穷多。

3.5 σ(*)与 σ 之间的关系

利用4.3.4中的方法不难得到下式：

4 Bessel公式第二类证法的改进

4.1 基本思路

Bessel公式解决用实验标准差s去估计总体标准差σ的问题。问题是s的表达式即Bessel公式：

如何得到？

上述思路是正确的。下面就按照这种思路对Bessel公式第二类证法进行改进。

4.2 改进的第二类证法

第一步，引入测得值误差、残余误差、算术平均值误差的概念。

定义：

称为测得值xi与真值μ的误差（不可测量）。

称为测得值xi与算术平均值的残余误差（简称残差）。

并定义测量列的算术平均值的误差（不可测量）为：

第二步，用残差vi和算术平均值的误差改造误差δi，寻找的替代式。

式（23）、（24）、（25）结合可得：

由式（26）可得：

因残差之和必为零，即有：

式（28）代入式（27）可得：

由式（26）、（28）可得：

当n充分大时，可以认为式（3）成立，理由如2.3中所述。式（3）代入式（30）可得式（2），式（2）代入式（29）可得：

解上式可得

第四步，用充分大的n替代极限运算，得到Bessel公式。

式（31）代入式（6）可得：

当n充分大时，可得到σ的估计值σ^的表达式，即Bessel公式：

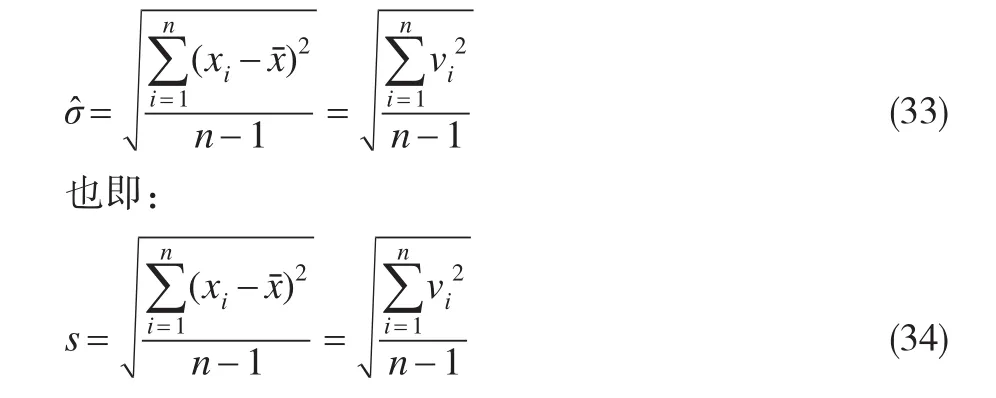
5 基于标准偏差的意义证明Bessel公式

5.1 问题的提出

从上述讨论可知，Bessel公式第二类证法及改进的证法中，仍然需要用到式（3）。而证明式（3）成立需要加限制条件：δi为无穷小量且对称分布。表面上看式（3）是关键，而实际上最关键的是式（2），式（3）只是为得到式（2）准备的。那么，有没有别的方法避开证明式（3）而得到式（2）呢？

文献[12-14]注意到了这一点，指出“深入分析标准差σ的本质和作用，可知σ是δi统计意义上的平均值”，因此可用 σ()来代替即有

由式（35）、（36）可得：

将式（37）代入式（29）结合σ的定义式可得到Bessel公式。

上述证明方法存在三个方面的问题，一是怎样深入分析标准差σ的本质和作用没有给出；二是没有给出σ()的定义及意义（这样便无法分析 σ()的意义）；三是 σ()恒为正值，可正可负，两者不可能恒相等。因而这类证法显得牵强附会，“凑证明”的味道很浓。实际上，文献[16]曾经利用式（37）证明过Bessel公式，但没有说明式（37）成立的理由。

因此，基于标准偏差的意义证明Bessel公式，必须先建立各种标准偏差的完整定义,明确它们的本质含义，并建立各种标准偏差之间清晰的逻辑关系，这样才能正确应用。

5.2 基于标准偏差的意义证明Bessel公式

证明的前面两步与3.4.2中相同，只是第三步消去δ的方法不同。

式（38）、（20）结合可得：

式（39）代入式（29）得：

即：

联立式（40）、（41）可得：

即有：

6 Bessel公式的适用条件

从我们提供的新证法中可得到以下几点结论：

（1）Bessel公式并不要求被测量或测量误差服从正态分布。但经典证法中由于要利用式（3），不得不要求测量误差服从对称分布，从而限制了Bessel公式的适用范围。

（2）Bessel公式成立需要测量的重复性或复现性条件能够充分保证，而且要求“等精度测量”这个条件。这一条限制是因为在证明过程中用到了式（20）的缘故。文献[17]指出不需要等精度测量”这个条件看来是有问题的，文献[18]谈不等精度测量的标准差的估计从另一个角度证明了Bessel公式的成立确实需要满足等精度测量这个条件。

（3）不要求测量列给出的是彼此不相关的测量结果，s应该只是给定条件下的数据的分散性。

（4）要求测量的次数足够多，以保证式（38）及式（41）能够很好的成立，从而保证用Bessel公式估计的σ有较高的精度。估计值s(xi)的相对标准偏差与测量次数的关系由下式给出

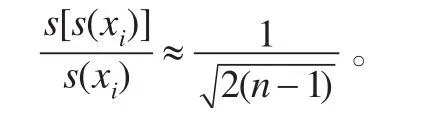
[1]毛英泰.误差理论与精度分析[M].北京:国防工业出版社,1982.

[2]肖明耀.误差理论与应用[M].北京:计量出版社,1985.

[3]龚镇雄.普通物理实验中的数据处理[M].西安:西北电讯工程学院出版社,1985.

[4]黄俊钦.测试误差分析与数学模型[M].北京:国防工业出版社,1985.

[5]Les Kirkup,Bob Frenkel.曾翔君,骆一萍,申淼译.An Introduction to Uncertainty in Measurement[M].西安:西安交通大学出版社,2011.

[6]〔日〕冈积满.测量误差计算[M].北京:人民铁道出版社,1975.

[7]费业泰.误差理论与数据处理[M].北京:机械工业出版社,(第六版),2010.

[8]王武义.误差原理与数据处理[M].哈尔滨:哈尔滨工业大学出版社,2001.

[9]马宏,王金波.误差理论与仪器精度[M].西安:陕西人民教育出版社,2007.

[10]朱鹤年.基础物理实验教程[M].北京:高等教育出版社,2003.

[11]王中宇,刘智敏,夏新涛,等.测量误差与不确定度评定[M].北京:科学出版社,2008.

[12]朱洪海.对贝塞尔公式证法的探讨[J].计量与测试技术,2001,28(6).

[13]马美娟.贝塞尔公式推导的再研究[J].佳木斯大学学报(自然科学版),2011,29(2).

[14]朱安远.各种估计总体标准差方法的误差分析和比较研究(上)[J].中国市场,2013,(10).

[15]邓永和.中误差贝塞尔公式的推导[J].大地测量与地球动力学,2009,29(3).

[16]刘智敏.误差与数据处理[M].北京:原子能出版社,1981.

[17]李慎安.测量不确定度百问[M].北京:中国计量出版社,2009.

[18]陶靖轩,顾龙芳,宋明顺,等.不等精度测量结果标准差的估计[J].计量学报,2012,33(1).