风险投资决策模型的参数组合研究

王超发，倪自力，孙静春

（西安交通大学 管理学院，西安 710049）

0 引言

风险投资的传统决策方法的基本思路是由风险项目的期望净现金流量和风险项目相适应的贴现率计算出项目NPV值。然而，NPV方法容易忽略公司具有战略意义的投资项目并依据今天的信息对未来做出决策，因此DCF(现金流折现法)容易低估风险投资项目的内在价值。为了弥补NPV方法的不足，Myer(1977)提出了实物期权：投资项目的价值不仅来自单个投资项目所直接带来的现金流，还来自成长的机会。因此，实物期权方法逐渐成为风险投资决策的主要依据。

虽然，实物期权决策法比传统的NPV法更接近现实。但是实物期权方法在风险投资领域中的应用中也遇到了一些困难。本文针对实物期权定价模型中的各种参数估计方法，依据实验设计，在假设对于同一项目的同类期权的数值法和解析法得到的期权价值是相同的条件下，构造一种实物期权定价模型参数的相关性以及交互作用的分析框架，解决了实物期权定价时关于模型参数估计和选择的问题。

1 风险投资中的期权定价模型参数分析

实物期权是在金融期权的基础上发展而来，最具代表性的期权定价模型是布莱克—舒尔斯（B-S）模型：

这里，N(·)为标准正态分布变量的累积概率分布函数。

在风险投资决策中，以上各参数及其估计方法都对应着企业的实际运作状况并且都有自己的现实意义：标的资产价格（项目价值）的波动率σ、项目资产价值S、投资成本X、无风险利率r以及到期时间T。其中，标的资产价格波动率的确定包括：用历史数据估计波动率、用项目价值倒推出隐含的波动率（由于实物期权的非交易性，因此实际中的隐含波动率较难获得）、用模拟方法估计波动率。项目资产价值的确定包括：假设资产价值变动是连续过程和假设资产价值变化是离散过程。投资成本的确定包括：随机型，确定型（常量，受时间的影响）。无风险利率的确定包括：用无风险的政府债券来确定、用其他证券进行估计、用税后利率的确定。到期时间根据项目投资有效期确定。

2 基于实物期权定价模型参数的实验设计与应用

在进行实物期权定价模型参数的实验设计之前先作以下的基本假设：

风险投资项目的到期时间T为已知常数；

对于同一项目的同种期权的解析定价法和数值定价法得到的期权价值是相同的；

对于一个风险投资项目的期权定价方法共有三种定价方法：B-S定价法、二叉树法、蒙特卡洛模拟法。

资产项目无价值漏损。

2.1 实验设计

将以上连续的变量进行离散化，则同一期权的定价可以分别采用B-S定价法、二叉树法和蒙特卡洛模拟法进行定价。设：A,B分别是以上四种因子（由于到期时间T为已知常数，则影响期权价值的主要因子为四个）中的不同的两种因子，它们分别有a和b种估计方法，即它们分别有a和b个水平。另外，由于同一项目的看涨和看跌期权的价值相差较大。因此，该实验的响应变量都应是同类型期权的价值。根据以上假设，可将两因子交互作用的析因实验设计如下：

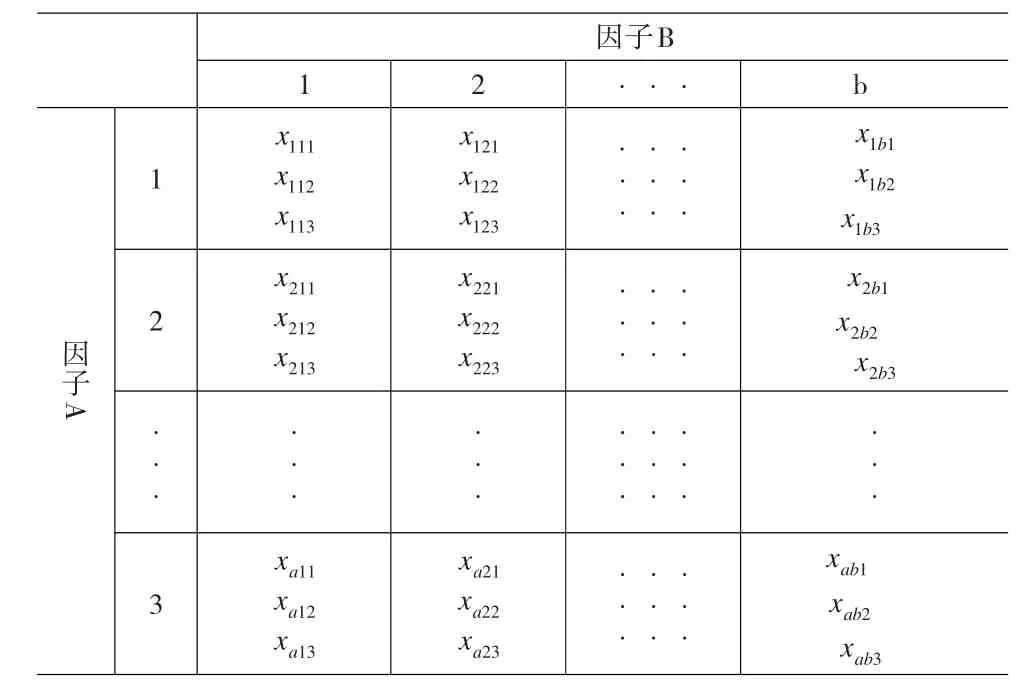
表1 两因子参数组合实验的ab个处理组合表

将平方和与自由度分别按它们的来源分解如下：

SST=SSA+SSB+SSAB+SSE

这里SSA表示因子A的平方和，SSB表示因子B的平方和，SSAB表示交互作用的平方和，SSE表示误差平方和。若记：处理 i（因子A）的样本均值为处理 j（因子B）的样本均值为，处理 i（处理A）和处理 j（因子B）组合的样本均值为，所有nT个观察值的总样本均值为。则有r个复制的两因子析因实验的ANOVA表如下：

表2 有r个复制的两因子析因实验的ANOVA表

根据以上析因实验的ANOVA表，我们设计的检验规则为：在显著性水平α下，原假设为H0:期权价值不存在显著性差异，备择假设为Hα:期权价值存在显著性差异。因子A对期权价值影响的显著性通过统计量检验，服从分子自由度为(a-1)，分母自由度为ab(r-1)的F分布。因子B对期权价值影响的显著性通过统计量检验，服从分子自由度为(b-1)，分母自由度为ab(r-1)的F分布。因子A、B对期权价值影响交互作用的显著性通过统计量检验，服从分子自由度为(a-1)(b-1)，分母自由度为ab(r-1)的F分布。

2.2 实验设计应用

某风险投资公司投资兴建一个光伏生产项目，虽然目前由于市场的不确定性项目仍处于亏损状态，但是作为目前世界各国对环境的重视，该企业决策者认为，光伏需求量有极大的增长潜力，在未来5年内公司需要不断投入8000万元以购置厂房、生产成本以及进行市场推广等。根据投资的预期现金流分析，该项目可带来5000万元的收入。从表面来看该项目投资是不利的，但经过专家分析，未来几年内光伏需求量将会急剧增长。所以，我们认为该项目的投资会产生扩张机会，即增长期权。投资该项目有未来进行先进入市场的机会，预计公司要比其他竞争者先进入市场时，仍然需要再投资2.2亿元，如果考虑整体宏观经济的变化预计投资成本为2.5亿元，如果考虑到管理费用和受时间影响，预计投资成本为2.7亿元。在现行市场信息的基础上，该公司组织专业人员对市场进行预测，得出的结论是，先进入市场所能产生的现金流的现值为2.4亿，如果假设标的资产价格变化过程服从连续过程，这时预测的现金流现值为2.6亿且不存在价值漏损。另外，根据金融市场同类型公司证券进行估计，光伏企业的价值年度平均标准差为48%，根据模拟法估计的年度标准差为35%。根据无风险债券确定的无风险利率为4.7%，根据税后利率确定的无风险利率为4.5%，通过金融市场上光伏企业发行的债券确定的收益率为5%。

对该风险投资公司来说，在其他变量取各种预测值的均值时，两因子交互作用的析因实验如下：

表3 A（σ）和B（X）

表4 A（σ）和B（S）

表5 A（σ）和B（r）

表6 A（S）和B（r）

表7 A（X）和B（r）

表8 A（X）和B（S）

表9 各因子实验的研究数据汇总表

将以上各表中的两因子实验研究数据汇总如下：

这里，MSA,MSB分别表示因子A和B的均方，MSAB表示因子A,B交互作用的均方，MSE表示误差的均方。

表10 各因子实验的均方数据汇总表

2.3 实验结果分析

从表10可以看到在显著性水平α=0.05下，表3中的因子A的均方对应的分子自由度是1，分母自由度是12，即对应的=4.75＞0.979337 ，表 4对应的5.32＞3.551552，表5对应的=4.75＞4.06800。所以，波动率的不同估计方法对期权价值有显著影响。

因此，对于单个因素的不同估计方法得到的结论是一致的，即以上因素的不同的估计方法对期权价值有显著的影响。

因此，在组合—波动率和投资成本、组合—投资成本和无风险利率以及组合—投资成本和项目资产价值的不同估计方法下，这三种组合对期权价值的交互作用影响不显著。在组合—波动率和项目资产价值、组合—波动率和项目资产价值以及组合—项目资产价值和无风险利率的不同估计方法下，这三种组合对期权价值的交互作用有显著的影响。

3 结论

通过以上的实验设计可以看到，影响期权价值的四个主要因素对期权价值的影响是显著的并且各因子组合的交互作用对期权价值的影响的显著性不同。所以，在实际针对实物期权价值进行计算时将变量进行主次之分是很有必要的。由于交互作用的存在，本文提出以下建议：如果波动率、项目资产价值和无风险利率其中之一的估计是可靠的，那么这时，其他两个变量的估计也应该应用更加切合实际的模型进行估计，而不能用常数代替。针对波动率、投资成本和无风险利率的估计，如果波动率是可靠的估计，那么此时的无风险利率应该采用可靠的估计，而此时的投资成本可以应用常数代替。另外，通过以上的分析可以将各因素对期权价值影响的显著性进行排序，即对期权价值有显著影响由强到弱分别为波动率、无风险利率、项目资产价值和投资成本。

[1]Myers S C.Determinants of Corporate Borrowing[J].Journal of Financial Economics,1977,5(2),

[2]Brealey R.Myers S C.Principle of Corporate Finance(5th ed.)[M].New York:Irwin McGraw-Hill,1996.

[3]Dixit A R.Pindyck.Investment Under Uncertainty[M].N.J:Princeton University Press,1994.

[4]David,K,Johnm,C.Real-Options Valuation for A Biotechnology Company[J].Financial Analysis Journal,2000,56(3),

[5]Eduardos S,Mark M.Rational Pricing of Internet Companies[J].Financial Analysis Journal,2000,56(3),

[6]Trigeorgis L.The Nature of Option Interactions and The Valuation of Investments With Multiple Real Options[J].Journal of Financial and Quantitative Analysis,1993(28),

[7]李献策，风险投资实物期权价值影响因素的灰色关联分析[J].决策参考，2009，(15).