On the role of topographic amplification in seismic slope instabilities

Fardin Jafarzadeh,Mohammad Mahdi Shahrabi,Hadi Farahi Jahromi

Civil Engineering Department,Sharif University of Technology,Azadi Avenue,Tehran,Iran

1.Introduction

Slope failure,as a result of inertial instability mechanism,is one of the most destructive seismic hazards.Pseudostatic and sliding blocks are the two most famous state-of-the-art procedures used for evaluation of seismic slope failures.Although pseudostatic approach is simple and straightforward,it only determines the potential for initiation of movement along a prede fined slip surface by giving a safety factor(Kramer,1996).

As permanent deformation analysis(Newmark,1965;Makdisi and Seed,1978)is placed between overly simplified pseudostatic and overly complex stress-deformation approaches(Clough,1960),it has been widely used by engineers in practice(Jibson,2011).The concept and applications of this method,which is based on the analogy of the sliding mass with a moving block on an inclined plane,were comprehensively discussed by many researchers(Lin and Whiteman,1986;Jibson,1993;Kramer and Smith,1997;Rathje and Antonakos,2011).

Though convenient for engineering purposes,permanent deformation procedure for dynamic slope stability evaluation only considers the effect of shear body waves(SV).However,Rayleigh wave is typically generated near soil slopes due to topographic effects on seismic wave propagation.

Uncommon damages have been reported and attributed to topographic amplification of earthquake motions in the 1971 San Fernando earthquake(Boore,1972),1982 Coalinga earthquake(Stewart and Sholtis,2005),1985 Chile earthquake(Celebi,1987)and 1999 Athens earthquake(Gazetas et al.,2002).Irregular geometry of the slope surface and its effect on Rayleigh wave propagation have been the subjects of considerable researches and discussions(Assimakiand Gazetas,2004;Bouckoval as and Papadimitriou,2005).The generated surface waves can significantly affect the response of soil slopes subjected to seismic waves(Uenishi,2010).

By verifying the Rayleigh wave generation in horizontally excited slopes,this paper tries to investigate the effect of surface Rayleigh waves combined with SV body waves generated by earthquake event on soil slopes.Although consequential,this phenomenon has gained less attention by scientists and there are relatively few reported studies in the literature.Herein, finite element analysis along with shaking table model tests is used to discover the fact.

Accordingly,topographic amplification effect on inertial forces acting on a sliding mass during seismic slope instability has been studied.Finally,the calculated slope displacements are compared with empirically predicted ones,and frequency dependent nature of dynamic slope deformations is recognised.

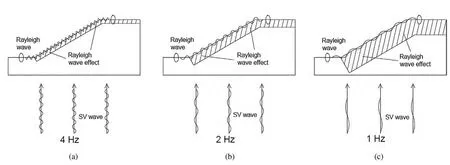
Fig.1.Effective depth of surficial amplification for(a)4 Hz,(b)2 Hz,(c)1 Hz incident SV waves.

2.Topography effects and Rayleigh wave generation

Seismic body waves are modified as they reach the earth’s surface due to topographic irregularities.High peak accelerations have been measured at different points along the surface and near the top of ridges,hills and step-like slopes in many earthquakes,such as a ridge in Matsuzaki,Japan(Jibson,1987)in which the average crest peak acceleration was 2.5 times the base acceleration near the toe of the ridge.Reflection and diffraction are considered to be the main causes of seismic wave amplification near soil slopes.Incident SH waves do not usually generate other wave types(e.g.P,SV and Rayleigh).In fact,SH waves can result in formation of Love waves under site-specific conditions which help trapping these waves inside a shallow near-surface layer(e.g.a soft layer upon a dense layer).On the contrary,propagating SV waves near slopes are reflected in the form of other wave types,especially Rayleigh surface waves.It has also been shown that amplification of SV waves can be much higher than that of SH waves(Assimaki and Gazetas,2004).

As reported by Ohtsuki and Harumi(1983),Rayleigh waves are generated by incident SV waves near the toe of the slope and then propagate along the surface towards the crest of the slope.It has also been stated that the generated Rayleigh waves behind the slope crest can have an amplitude of up to 35%-40%compared to that of the incident waves.However,based on the interaction of various reflected and diffracted waves,analysis of topographic amplification and deamplification is a complicated issue.In fact,patterns of topographic effects rely upon the geometry of the irregularity and upon the types,frequencies,and angles of incident waves(Sanchez-Sesma and Campillo,1993).Consequently,there are a few systematic studies in that context which gave a clear insight to consider the effect of each wave separately.

In any case,it is accepted that Rayleigh surface waves are generated in the vicinity of soil slopes due to diffraction of incident SV waves.Horizontal and vertical displacement amplitudes of Rayleigh waves clearly show that there is an effective depth,approximately equal to the wavelength(λR),to which these waves produce considerable motions.Keeping in mind the fact that the generated Rayleigh waves impose inertial forces on the sliding mass in addition to those by the incident body waves,the significance of the above mentioned surface wave characteristic is magnified.Hereafter,the depth beneath a slope surface to which the diffracted Rayleigh waves generated by the incident SV waves result in additional accelerations and inertial forces,is referred to as the “effective depth of surficial amplification”.

Within the rigid block theory proposed by Newmark(1965)for evaluation of seismic slope displacements,it was originally assumed that the “failure mass”is rigid;however the materials that comprise most slopes are rather compliant.The extent to which the assumption of rigid “failure mass”remains accurate depends on the wavelength of the input motion compared to the size of the potential sliding mass(Kramer and Smith,1997).For thin failure masses and/or long wavelengths(low input frequencies),motions within the sliding mass are in phase and the effects of failure mass compliance are small.In a different manner,for thick failure masses and/or short wavelengths(high input frequencies),the effect may be significant and the fact that the resulting driving force acting on the potential failure mass is not proportional to the acceleration of each individual point within the mass,clearly shows the importance of frequency-dependent nature of seismic response of slopes.To account for the effect of frequency content of the input motion,Yegian et al.(1991)proposed the following normalised expression for the permanent deformation of slopes by using Newmark’s sliding block analysis and recorded acceleration time histories:where u*is the normalized permanent deformation,u is the total relative deformation,ayis the yield acceleration,amaxis the peak acceleration,Neqis an equivalent number of cycles,and T is the predominant period of the input motion.

Within the concept of the effective depth of surficial amplification,another critical aspect of frequency-dependent nature of seismic slope failure can be developed.As discussed before,the generated Rayleigh waves increase induced accelerations to a specific depth beneath the surface of the slope directly proportional to the predominant wavelength of the input motion(inversely proportional to the predominant frequency).Hence,it can be summarised that the smaller the predominant frequency of the input motion,the larger the area(mass)affected by the generated Rayleigh waves near the slope(Fig.1).This phenomenon leads to greater inertial forces acting on the sliding mass;thus larger induced displacements occur.In fact,this assertion is consistent with the above equation proposed by Yegian et al.(1991).Both of them suggest that the lower predominant period of input motion causes larger displacements.

In summary,an important aspect of topographic amplification and Rayleigh wave generation adjacent to ridges,embankments and step-like slopes,the key characteristic of surface waves,is the effective influence depth.This fact is another proof for the frequency-dependent nature of seismic slope instabilities.In what follows,some pieces of evidences are presented for this claim by using the results obtained by some numerical and shaking table physical models.

Fig.2.Geometry and material characteristics of the prototype slope.

3.Physical model

In order to evaluate the response of a slope subjected to seismic loading,a small-scale 1 g shaking table physical test was designed and performed in Geotechnical Earthquake Engineering Laboratory of Sharif University of Technology(Farahi Jahromi et al.,2013).The small-scale slope geometry,material properties and loading characteristics resemble a prototype target slope exposed to an anticipated earthquake excitation in the northwest of Tehran.The following sections introduce the geometry and material characteristics of prototype slope,along with the predicted site-specific earthquake.Subsequently,similitude law,its application and physical model results are presented.The small-scale dynamic responses are converted to the full-scale ones and used for numerical model validation.

3.1.Target slope and loading characteristics

The target slope,which has 30°inclination and 8.7 m height,is composed of dense granular material with 15.5 kN/m3unit weight,30°friction angle,0.6 kPa cohesion,556 MPa maximum elasticity modulus and 0.3 Poisson’s ratio(Fig.2).The computed horizontal yield acceleration of the potential sliding mass(0.110 g)will be used in predictive equations of the maximum slope displacement.

The loading characteristics were selected from seismic hazard analysis reports allotted for Tehran with a 975-year return period(5%probability of exceedance in 50 years).The predicted excitations have 0.49 g peak acceleration and 3.8 Hz predominant frequency(TGC,2012).

Table 1Characteristics and instrumentation of the physical model.

3.2.Similitude law and small-scale model

As the similitude analysis is of great importance in model dimensions and loading level selection,it is performed based on Iai method(Iai,1989;Iai et al.,2005).By the assumption of the geometrical scaling factor(λ=10),the shear wave velocities of the model and prototype(50 m/s and 375 m/s,respectively),and the similar soil densities(λρ=1), λεand model dimensions were calculated.Table 1 summarises the assumptions of similitude calculations.

A small-scale dynamic 1 g shaking table test was performed on a slope model composed of non-cohesive granular material(Babolsar coastal sand).The poorly graded sand has less than 3% fines,1420-1750 kg/m3density and 5%moisture in the laboratory.For model preparation,the air pluviation method was used and a pouring height of 70 cm was calibrated and used in order to reach the target density and uniformity.A rigid box(300 cm×100 cm×150 cm(L×W×H))composed of steel profile and plates was used as a soil container.Besides,a Plexiglas plate installed on one side of the box allowed the slope deformation to be monitored(Farahi Jahromi et al.,2013).

The slope deformations were visually measured from displacements of plaster strips poured in each 10 cm layer adjacent to Plexiglas plate(Fig.3).The properties,physical characteristics and instrumentation of the slope model are summarised in Table 1.According to Seed approach(Kramer,1996)and similitude calculations,the sandy slope was subjected to an artificial sinusoidal loading of 25 cycles with 0.32 g amplitude(65%of the anticipated peak amplitude)and 5 Hz frequency.

Dynamic slope responses were recorded by accelerometers and LVDTs installed in the slope.The maximum horizontal displacement of the sliding mass,vertical displacement of slope crest and acceleration time histories of slope’s toe(accelerometer ACC4)and crest(accelerometer ACC9)were used for empirical analysis and large-scale finite element model verification(Fig.4).

4.Full-scale finite element models

The full-scale prototype slope was simulated and analysed by the finite element based ABAQUS programme.The slope material properties were selected as those assumed for the target slope(prototype parameters indicated in Table 1).In order to make the numerical model more comparable to actual field conditions,lateral earth pressures and absorbent boundaries were assigned to the sides of the slope(Fig.5).Absorbent boundaries were defined by springs and dashpots at nodal points and the corresponding stiffness and damping coefficients were calculated(Meek and Wolf,1992).The above-mentioned coefficients are functions of material stiffness and influence area in each node.

Modulus reduction curves were used to define the nonlinear behavior of the soil.EPRI guidelines(EPRI,1993)for sandy soils were used to determine the cyclic shear strain dependency of elastic moduli at various depths.Moreover,low-strain stiffness(E0)in non-cohesive soils is known to be directly proportional to the vertical effective stress by the following equation(Das,1985):

where E1and E2are the stiffness moduli at two different points with vertical stresses ofσ1and σ2,respectively.As a result,the low-strain elasticity modulus increases with depth.Fig.6 presents combined effects of cyclic shear strain and vertical effective stress on Young’s modulus for various depths of the numerical model.According to Ishibashi and Zhang(1993),cyclic shear strain-dependent material damping was also assigned to the sandy soil.

Fig.3.Constructed physical model of slope.

4.1.Results and validation

In order to validate the results of finite element modelling,a verification was made using the relevant outputs from the physical test and the numerical analysis.Observed accelerations and displacements were converted and compared to the pertinent full-scale ones respectively.Fig.7 shows calculated accelerations at analogous points of ACC4 and ACC9 in the numerical model.As the similitude scaling factor for induced accelerations is one,those of small-scale and large-scale models can be compared directly.It has to be noted that the scaling factor affecting the frequency cycles causes an increase in the cyclic loading time of the largescale model by a ratio of 1.38（λλ0.5εIn Fig. 7, the maximum horizontal displacement of the sliding mass,and the vertical displacement at the slope crest measured in the large-scale numerical model are reported.In order to convert these values to small-scale ones,a factor of 1/1.8(1/（λλε）)should be applied.The results indicate a good precision and errors were less than 30%for peak accelerations recorded at the toe(ACC4)and the crest(ACC9)of the slope,peak horizontal displacement and crest’s vertical deformation.

Fig.4.Typical dynamic response of the physical model.

4.2.Evidence for Rayleigh wave generation

Geometric irregularities are proved to influence incident waves and generate Rayleigh waves near a slope subjected to SV waves.Herein,some indications of such effect in both physical and numerical models are presented and discussed.

It is interesting to consider the frequency response of recorded accelerations in both physical and numerical models.As predicted,the highest amplitudes in smoothed fast Fourier transforms(FFTs)of accelerometer ACC4 in the physical test and the numerical model are observed at the loading frequencies of 5 Hz and 3.8 Hz,respectively(Figs.8a and 9a).However,Fig.8b shows that in accelerometer ACC9,secondary waves with considerable amplitudes at higher frequencies than that of the input motion are generated(e.g.10 Hz,15 Hz and 20 Hz).A similar observation is shown in Fig.9b which is related to the recorded acceleration in ACC9 in the numerical model.The variation in Fourier spectrum,along with high amplifications in the slope crest,is a sign of Rayleigh wave generation caused by diffraction of incident SV waves.

As discussed before,an important characteristic of Rayleigh waves is the depth to which they penetrate under the surface of propagation.This depth is approximately equal to their wavelength.Therefore,for waves with a lower predominant frequency(longer wavelength),amplifications due to Rayleigh wave generation influence the subsurface material to a greater depth.This concept can be referred to as the“effective depth of surficial amplification”,and has gained less attention in analyses of seismic slope stability.Using the verified large-scale numerical model and input motions of constant amplitudes(0.32 g),a frequency analysis was conducted and the model was shaken to various frequencies of 1-10 Hz.Fig.10 graphically shows computed accelerations in models with exciting frequencies of 1 Hz,3.8 Hz and 10 Hz.The wave fronts of Rayleigh waves for each model are specified with circles.The depths to which horizontal accelerations were increased clearly show the influence depth of surface waves.This evidence can better prove the frequency-dependent nature of topographic(geometric)amplifications acting on any slope,and in fact,on a given sliding mass within the slope.The schematic view in Fig.10 indicates that input motions with greater wavelengths can have more destructive effects on slopes,not only as a consequence of in phase driving forces acting on the sliding mass(Kramer and Smith,1997),but also as a result of greater influence depths of generated Rayleigh waves.

Fig.5.Boundary conditions assigned to the numerical model.For clarity,lateral earth pressures are sketched between sections a-a to b-b,and springs/dashpots between sections c-c to d-d.

Fig.6.Modulus reduction curves for typical depths(h).

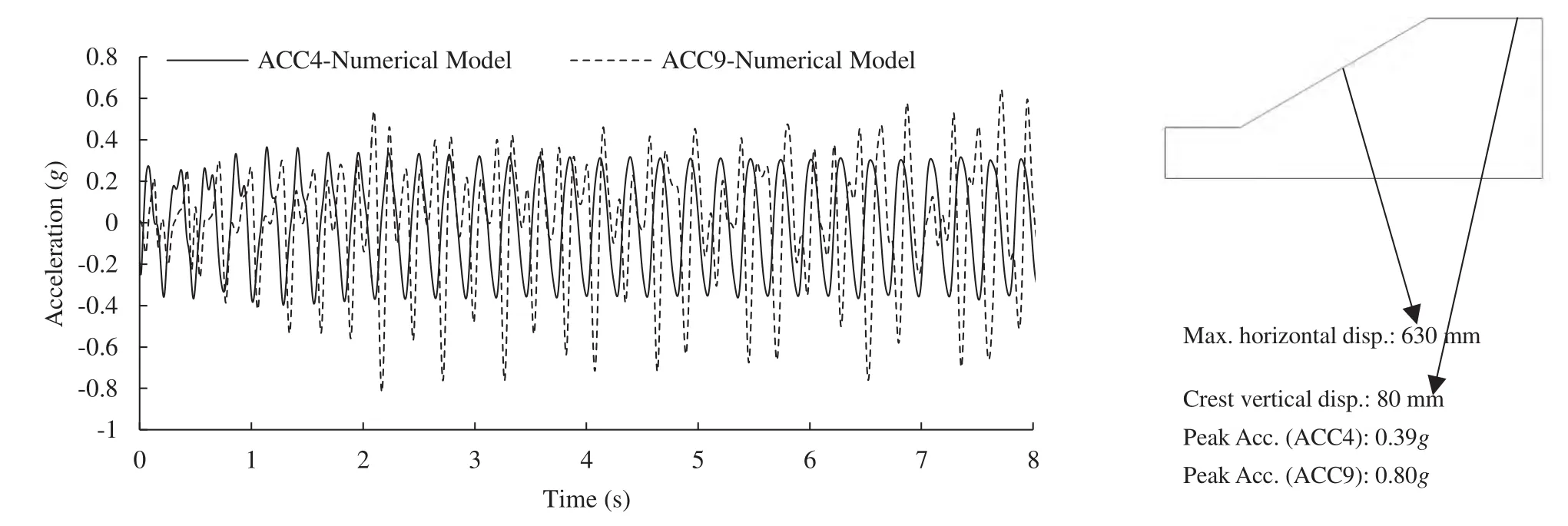
Fig.7.Typical dynamic response of the large-scale numerical model.

Fig.8.Smoothed fast Fourier transform of ACC4 and ACC9 in the physical model.

Fig.9.Smoothed fast Fourier transform of ACC4 and ACC9 in the full-scale numerical model.

Fig.10.Horizontal accelerations(m/s2),influence depth of Rayleigh waves generated near slopes subjected to input motions with frequencies of(a)10 Hz,(b)3.8 Hz and(c)1 Hz.

4.3.Deformation analyses

Full-scalefinite element model displacement results are compared with those obtained by some classical permanent deformation analyses.It is important to note that most of these methods assume the response to be frequency-independent.However,as discussed earlier,there seems to be an elapsed connection between the frequency content of an input motion and displacement response of an earthquake induced landslide.The results of frequency analyses support the idea that lower frequency(higher wavelength)excitations lead to greater horizontal displacements(Fig.11).

Predicted horizontal displacements of Makdisi-Seed method(Makdisi and Seed,1978)are in the range of 95-606.5 mmwith the average value of 173 mm(for all input frequencies).Similarly,Ambraseys-Menu formula(Ambraseys and Menu,1988)anticipated a value of 244.8 mm.When compared to the results of the numerical models,these estimates mostly underestimate the actual displacements.

On the contrary,Yegian et al.(1991)approach seems to better reflect the effects of frequency content in earthquake induced displacements(Fig.11).Nonetheless,it seems to greatly overestimate the permanent displacement of a slope when subjected to low frequency loadings(lower than 2 Hz).

5.Conclusions

The earthquake induced displacement of a sliding mass is an important parameter used to assess the seismic performance of slopes(Rathje and Antonakos,2011).Commonly,most of the predictive models use the bedrock peak acceleration for slope’s horizontal displacement calculations.Some of these models modified their predictions by taking acceleration amplifications into account.Nevertheless,incident body wave diffraction near slope surface is neglected,a phenomenon which converts the propagating body waves in the form of Rayleigh surface waves and greatly influences the slope’s dynamic response pattern.

This paper evaluates the significance of the“effective depth of surficial amplification”and its influence on the seismic performance of slopes.As the influence depth is directly proportional to wavelength,the frequency-dependent nature of seismic slope instabilities seems indispensable.

On this subject,a 1 g shaking table test and numerical analyses are performed to examine the generation of surface waves near the slope.Then,the impact of predominant frequency and effective depth of the input motion on permanent horizontal displacements of the slope is studied.The following conclusions can be drawn:(1)Topographic amplification can greatly increase the induced accelerations on the surface of a slope and most significantly on its crest.

(2)Generated Rayleigh waves near the slope toe propagate upwards to the slope crest,where they meet preceded Rayleigh waves produced on the horizontal surface of the crest.

(3)The accuracy of methods to predict the earthquake induced permanent deformation of a slope can be increased by considering the topographic amplification phenomenon.

(4)Based on the fact that wavelength affects the influence depth of surface waves,and it itself is totally dependent on the frequency content of the wave,seismic slope instabilities undoubtedly have frequency-dependent nature.

It is important to note that the classical procedures of seismic permanent deformation assessment of slopes are best performed if the average horizontal acceleration induced in the sliding mass is implemented(by considering both incident and diffracted/reflected waves).However,exact prediction of such quantity seems difficult to be achieved,since it is affected by many parameters such as the geometry of the irregularities and the types,frequencies,and angles of incident waves.

Conflict of interests

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgements

The authors deeply appreciate Tehran Gas Company(TGS)’s authorities who introduced the research project and financially supported the physical tests and numerical modelling expenses.Also they thank Dr.Davoudi’s instructions who guided the research group as the TGS’s representative.

Ambraseys NN,Menu JM.Earthquake-induced ground displacements.Earthquake Engineering and Structural Dynamics 1988;16(7):985-1006.

Assimaki D,Gazetas G.Soil and topographic amplification on canyon banks and the 1999 Athens earthquake.Journal of Earthquake Engineering 2004;8(1):1-43.

Boore DM.A note on the effect of simple topography on seismic SH waves.Bulletin of the Seismological Society of America 1972;62(1):275-84.

Bouckovalas GD,Papadimitriou AG.Numerical evaluation of slope topography effects on seismic ground motion.Soil Dynamics and Earthquake Engineering 2005;25(7-10):547-58.

Celebi M.Topographic and geological amplifications determined from strongmotion and aftershock records of the 3 March 1985 Chile earthquake.Bulletin of the Seismological Society of America 1987;77(4):1147-67.

Clough RW.The finite element method in plane stress analysis.In:Proceedings of the 2nd Conference on Electronic Computation.Pittsburgh,USA:ASCE Structural Division;1960.

Das BM.Advanced soil mechanics.McGraw-Hill;1985.

Electric Power Research Institute(EPRI).Guidelines for determining design basis ground motions.Final Rep.No.TR-102293.Palo Alto:California;1996.

Farahi Jahromi H,Joshaghani M,Sehi-Zadeh M,Yousefi S.Comparison of dynamically-induced experimental slope deformations with numerical sliding block theory.In:Proceedings of the 5th International Young Geotechnical Engineering Conference;2013.Paris,France.

Gazetas G,Kallou PV,Psarropoulos PN.Topography and soil effects in the Ms5.9 Parnitha(Athens)earthquake:the case of Adames.Natural Hazards 2002;27(1-2):133-69.

Iai S.Similitude for shaking table tests on soil-structure- field model in 1 g gravitational field.Soils and Foundations 1989;29(1):105-18.

Iai S,Tobita T,Nakahara T.Generalised scaling relations for dynamic centrifuge tests.Geotechnique 2005;55(5):355-62.

Ishibashi I,Zhang X.Unified dynamic shear moduli and damping ratios of sand and clay.Soils and Foundations 1993;33(1):182-91.

Jibson RW.Summary of research on the effects of topographic amplification of earthquake shaking on slope stability.Menlo Park,CA:US Geological Survey Open-File Report;1987.p.87-268.

Jibson RW.Predicting earthquake-induced landslide displacements using Newmark’s sliding block analysis.Transportation Research Record 1993;1411:9-17.Jibson RW.Methods for assessing the stability of slopes during earthquakes-A retrospective.Engineering Geology 2011;122(1-2):43-50.

Kramer SL.Geotechnical earthquake engineering.Prentice-Hall;1996.

Kramer SL,Smith MW.Modified Newmark model for seismic displacements of compliant slopes.Journal of Geotechnical and Geoenvironmental Engineering 1997;123(7):635-44.

Lin JS,Whiteman RV.Earthquake induced displacements of sliding blocks.Journal of Geotechnical Engineering 1986;112(1):44-59.

Makdisi FI,Seed HB.Simplified procedure for estimating dam and embankment earthquake-induced deformations.Journal of Geotechnical Engineering 1978;104(7):849-67.

Meek JW,Wolf JP.Cone models for homogeneous soil,I.Journal of Geotechnical Engineering 1992;118(5):667-85.

Newmark NM.Effects of earthquakes on dams and embankments.Geotechnique 1965;15(2):139-60.

Ohtsuki A,Harumi K.Effect of topography and subsurface inhomogeneities on seismic SV waves.Earthquake Engineering and Structural Dynamics 1983;11(4):441-62.

Rathje EM,Antonakos G.A unified model for predicting earthquake-induced sliding displacements of rigid and flexible slopes.Engineering Geology 2011;122(1-2):51-60.

Sanchez-Sesma M,Campillo M.Topographic effects for incident P,SV,and Rayleigh waves.Tectonophysics 1993;218(1-3):113-25.

Stewart JP,Sholtis SE.Case study of strong ground motion variations across cut slope.Soil Dynamics and Earthquake Engineering 2005;25(7-10):539-45.

Tehran Gas Company(TGC).Geological and seismological reports of Tehran.2012.Tehran,Iran.

Uenishi K.On a possible role of Rayleigh surface waves in dynamic slope failures.International Journal of Geomechanics 2010;10(4):153-60.

Yegian MK,Marciano E,Ghahraman VG.Earthquake-induced permanent deformations:probabilistic Approach. Journal of Geotechnical Engineering1991;117(1):35-50.