我国科学研究与试验发展(R＆D)投产机制分析——基于R软件的PLS实证研究

安蕾袁鹏(云南财经大学，云南 昆明 650221)

1. 引言

科学研究与试验发展(R＆D)能力是衡量一个国家科技创新实力及核心竞争力的关键指标，而科技投入体制对一国的科技发展水平起到决定性作用。针对这方面的研究，国内外的学者都取得了丰富的成果。Griliches(1979，1986)［1，2］提出知识生产函数，认为科研产出是研发资本及人力投入的结果。Hitt等(1996)［3］研究发现企业自主创新能力随着研发经费投入的增加而增加。Inonu(2003)［4］以每百万人口的学术出版物数量及人均GDP为标准分类，对经济发展、文化因素与科研产出的关系进行阐述。在国内，余昕等(2007)［5］把SCI来源期刊论文量定为科研产出指标，通过对面板数据建立起科研投入产出关系模型，从定量的角度分析发达国家科研产出、科研经费投入、科研人员数及时间等因素的关系。李燕萍等(2009)［6］从环境因素、科研人员、科研经费投入、科研产出四要素的角度建立了影响科研经费有效使用的立体模型。

虽然相关的理论及实证研究较为丰富，但尚存在一些问题。例如科研的投入指标之间并非相互独立，很多情况下存在多重共线性，直接建模可能导致模型的不稳定。另外，现有的研究大多针对单一的产出指标进行影响因素分析，这种不全面的分析可能会导致结果的偏误。在方法的选择上本文尝试使用偏最小二乘回归，一方面该方法可以解决投入指标间存在的多重共线性问题;另一方面，由于本文从多个角度选取投入、产出指标，按经济发展情况分区域构建多个自变量对多个因变量的模型，以期尽可能全面系统的分析科研活动投入体制及各产出指标之间的关系，导致出现分组后样本数少于变量数的情况，而偏最小二乘回归也能很好的解决这一问题。

2. 指标的确定

本文数据来自于《中国统计年鉴》及《中国科技统计年鉴》(2013年)，实际数据为2012年全国31个省市自治区数据。

根据《中国统计年鉴》科学研究与开发机构部分，研究与试验发展(R＆D)投入情况分为人员及经费。结合近年来科研人员对我国科技投入体制的研究［7］，R＆D活动投入指标我们从执行部门、研究方向、及经费来源三个方面进行选取。产出指标从不同的研究机构或执行部门的产出类别进行选取。R＆D投入及产出指标如下表所示。

表1 科学研究与试验发展(R＆D)投入—产出指标表

3. 方法的选择

3.1 多重共线性判断

考虑到各地区发展情况有很大差异，可能会对模型结果的准确度有影响，我们将样本分为东部经济较发达地区(8个省市:北京、天津、辽宁、上海、江苏、浙江、山东、广东)及中西部发展地区(余下23个省市)。选取的指标中，自变量有15个，4个因变量，对东部发达地区建模时，样本个数少于变量个数。另外，考虑到投入指标间往往存在多重共线性，为保证模型的稳定性，我们在建模初要进行共线性判断。目前有许多常见的多重共线性诊断方法，例如最常见的对自变量的相关系数矩阵进行诊断的方法表明，当自变量间的二元相关系数值很大时，则判定变量间存在多重共线性。然而由于此法中关于相关系数的具体值与共线性的关系无准确的标准，有时即使相关系数值并不太大，但也不能排除准确说不存在多重共线性。另外，容忍度(tolerance)、方差膨胀因子(variance inflation fator，VIF)、条件数(condition number)等都可以作为准则来度量多重共线性。这些判断准则可能不一致，但不失为一个参考。本文采用条件数判断多重共线性，常用κ表示，定义为:

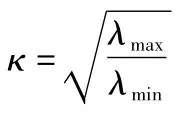
式子中，λ为XTX的特征值(X代表自变量矩阵)，一些研究者认为，当κ＞15时有共线性问题，κ＞30时，说明共线性问题严重［8］。

如果数据存在多重共线性问题，常用的处理方法有比较经典的主成分分析、逐步回归法及岭回归、lasso回归等。然而针对我们的数据特征，本文选择使用偏最小二乘回归法(PLS)。在20世纪70年代挪威统计学家Herman Wold在研究经济学中提出了偏最小二乘回归法，它能够对多变量对多变量的情况进行回归建模，特别的，在样本较少的情况下也能进行。目前有许多软件都可以进行偏最小二乘回归的运算，还有专门的SIMCA-P软件。但为了更好地普及偏最小二乘回归，本文所有分析都通过可以从网上免费下载的自由软件R来实现。

3.2 偏最小二乘回归

为了研究因变量和自变量之间的统计关系，设有p个自变量{x1，…，xp}和q因变量{y1，…，yq}，取n个样本观测点，那么自变量与因变量就构成了数据表X={x1，…，xp}n×p和Y={y1，…，yq}n×q。为了回归分析的需要，偏最小二乘回归方法先分别在X与Y中提取出成分t1(t1是x1，…，xp的线性组合)和u1(u1是y1，…，yq的线性组合)，并要求其需要同时满足两个条件:

3.2.1根据主成分分析原理，为了能够代表数据表X和Y，首先要求t1和u1应尽可能大地携带它们各自数据表中的变异信息:

Var(t1)→max

Var(u1)→max

3.2.2其次要求从自变量中提取的成分t1要在很大程度上能解释对从因变量中提取的成分u1，即要求t1和u1的相关性能够达到最大:

r(r1，u1)→max

首对成分提取后，偏最小二乘回归分别实施自变量X对t1的回归以及Y对t1的回归，如果回归方程已经达到满意的精度则算法终止，否则将利用 X、Y被t1解释后的残余信息进行第二轮的提取，直到能达到一个较为满意的精度。

最后，偏最小二乘回归将通过实施yk(k=1，…，q)对从X中提取的m个成分:t1，t2，…，tm进行回归，进而表达成yk关于原自变量 x1，…，xp的回归方程［9］。

3.3 因子数的确定

由于过多的成分可能会出现过拟合现象，因此很多时候，偏最小二乘回归法并不对全部的成分:t1，t2，…，tA进行回归。因此对于成分数的确定我们就需要有一个标准来进行判断，通常我们使用交叉验证的方法。常见的交叉验证法有“留一验证”，“K折交叉验证”，“Holdout验证”等。

交叉验证法将所有样本点随机的分成两部分:第一部分称训练集，用来重新拟合一个偏最小二乘模型;第二部分称测试集，将样本作为测试数据带入已经建好的拟合模型，并求出预测值误差平方和:，为了将所有的样本都预测一次，我们利用上述方法重复进行g次，最后将每个样本的预测误差平方和进行加总构成PRESS［10］:

本文选取“留一验证”来计算不同成分数对应的PRESS值，选择在成分数尽可能小的情况下，PRESS最小或几乎不变所对应的成分个数m，再调整模型重新进行pls回归。

3.4 回归系数的显著性检验

偏最小二乘回归不同于一般的最小二乘法，它的回归系数方差无法得到准确的无偏估计，Miller R.G.(1974)［11］提出了用来估计回归系数的方差的方法:Quenouille-Tukey jackknife。与此方法相对应的，我们在R软件的pls包中选取函数jack.test检验回归系数的显著性。

4. 实证分析

用R软件中的pls程序包对整理后的两组数据分别进行偏最小二乘回归建模分析。

4.1 中西部发展地区建模

4.1.1共线性判断

中西部发展地区我们抽取23个省市进行分析，15个投入指标，4个产出指标。读入数据后使用R固有的函数kappa()计算条件数κ，进行共线性判断。代码如下:

w=read.csv(″12发展.csv″，header=T)

kappa(w［，1:15］)

通过R软件计算得到:数据w的条件数κ=7225313，远大于30，可见R＆D投入指标间存在严重的多重共线性问题，因此我们就不尝试简单回归，采取偏最小二乘回归法对该数据进行回归建模。

4.1.2标准化数据

由于我们选择的R＆D投入指标存在单位不一致问题，为了消除量纲影响，我们在建模前先使用R软件中scale()函数对原数据进行标准化处理，同时也方便后续结论的分析。

4.1.3初步偏最小二乘回归及因字数确定

对标准化后的数据，先将所有因字数选入模型进行初步偏最小二乘回归，观察各因子数所对应的情况，再利用交叉验证准则进行因子数的确定。代码如下:

library(lars)

library(pls)

ap=plsr(Y～X，15，validation=“LOO”，jackknife=T)#进行偏最小二乘回归

summary(ap，what=“all”)#显示回归结果

validationplot(ap)#以图形显示不同因子数对应的PRESS值

R软件的运行结果中包含:使用留一交叉验证法(validation=“LOO”)计算的PRESS值，及不同因子数下拟合模型所对应的各个变量的解释度，选取部分回归结果如下表、图所示:

表2 发展省市初步偏最小二乘回归部分结果

图1 中西部发展省市不同成分数对应的均方误差图

根据上图、表我们可以看出，对R＆D产出指标建模时，当因字数为1，PRESS=0.1873最小，且根据交叉验证的原理:在成分数尽可能小情况下，大部分因变量在因字数为1时PRESS值为最小。此时1个因子对各因变量的累计贡献率也基本达到了80%，由此偏最小二乘回归改进模型的因字数m=1。

4.1.4 改进模型

根据前文选定的因字数进行模型的改进并再次进行偏最小二乘回归，代码如下:

pls2=plsr(Y～X，ncomp=1，validation=＇LOO＇，jackknife=T)#因字数ncomp取1

coef(pls2)#看回归系数

由于数据进行过标准化处理，得出的回归方程没有截距项，R运行得到回归系数表:

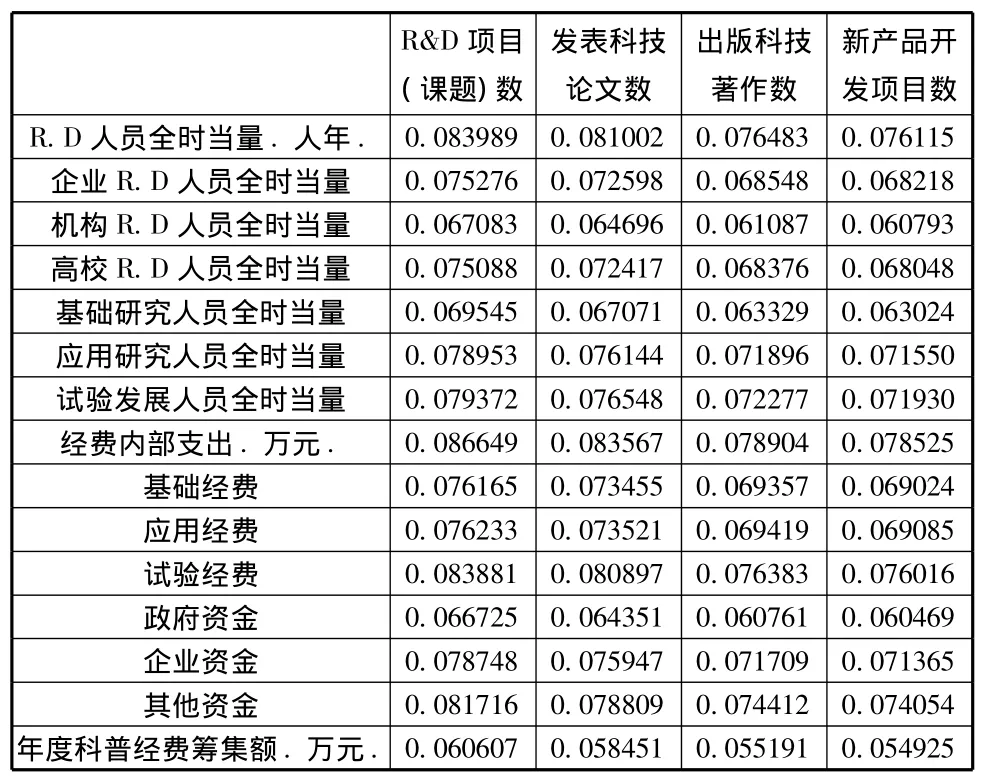
表3 中西部发展省市偏最小二乘回归系数表

根据回归系数表可写出2012年发展省市针对各因变量的回归方程(由于篇幅限制，因变量的回归方程略)。由于数据在回归前进行过标准化处理，我们可以直接看回归系数来初步判断各自变量对因变量的影响机制，通过对比我们发现:①对于中西部发展地区，经费内部支出是影响R＆D各产出指标最重要的因素(标准化后回归方程的系数最大)，其次是R＆D人员全时当量。这也与实际情况相符，对于经济欠发达地区，科技投入利用率不高，提高产出主要靠大量增加人力物力投入的粗放型经济发展模式，科技投入的不足严重制约了各省的科技创新能力的提高和科技事业的发展。

②投入指标按执行部门或研究机构来看，相对于研究机构及高等学校，企业对中西部发展地区科技产出的影响更大，该地区应该重视企业在科技创新中的作用，鼓励企业积极参与科技创新。③从资金来源看，影响中西部地区科技产出的最重要因素是企业资金及其他资金，我们应该在确保政府科技投入的前提下，启发企业及社会其他资源的投入。

4.1.5回归参数的显著性检验

为检验回归参数的显著性，我们使用R软件jack.test()函数，并将各回归系数对应的自变量显著情况整理如下表:

表4 中西部省市R＆D投入指标显著性表

R＆D项目(课题)数 论文 著作 新产品开发项目数政府资金＊＊＊ ＊＊＊ ＊＊＊ ＊＊＊企业资金＊＊＊ ＊＊＊ ＊＊ ＊＊＊其他资金＊＊＊ ＊＊＊ ＊＊＊ ＊＊＊年度科普经费筹集额.万元.＊＊＊ ＊＊＊ ＊＊ ＊＊＊Signif.codes:0‘＊＊＊’0.001‘＊＊’0.01‘* ’0.05‘.’0.1‘’1

根据上表及回归方程的参数符号我们可以看出:对于中西部发展省市，各科技投入指标对产出都起到很明显的促进作用，这与该地区的发展情况相符合，这些地区经济发展相对落后，R＆D人力物力资源都相对匮乏，对科技创新的意识有待加强，因此这些投入指标稍微增加都会对发展中地区的科技产出起到很明显的推动。

4.1.6拟合效果分析

①我们用R软件中predplot()函数画出最终模型的预测效果图，纵坐标为各因变量的预测值，横坐标为因变量的实际测量值，因此散点越集中在对角线上，说明模型的预测效果越好。

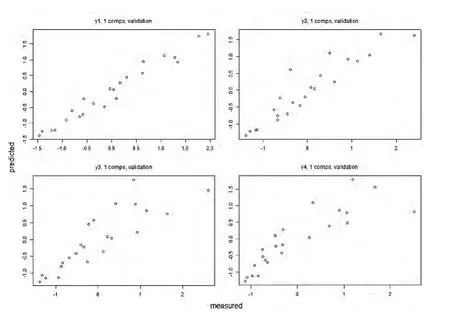
图2 中西部发展省市偏最小二乘回归拟合效果图

根据上图我们看出，对于各个R＆D产出指标，4张预测图的散点大都分布在对角线位置，可见最终模型的拟合效果较好。

②通常为了判断模型的拟合优度，大家也使用可决系数R2，我们认为R2的值越接近1，说明回归直线对观测值的拟合程度越好。我们也可以使用R软件来计算各因变量对应的R2，代码如下:

pls2=plsr(y1～.，data=w，ncomp=1)

yp=predict(pls2，data=w)［，，1］

RF1=sum((mean(w$y1)-yp)^2)/sum((w$y1-mean(w$y1))^2);RF1

将计算出的拟合优度整理如下表所示:

表5 中西部发展地区模型拟合优度表

根据上表我们也可看出，使用偏最小二乘回归构建的模型对各因变量实际观测值的拟合程度都达到71%以上，模型拟合效果较好。

4.2 东部发达地区建模

4.2.1共线性判断

选取八个经济较为发达的东部沿海省市(北京、天津、辽宁、上海、江苏、浙江、山东、广东)进行建模，15个自变量，4个因变量，建模过程与中西部发展省市类似，代码略。首先我们对自变量进行共线性判断，计算结果κ=1486.796，远大于30，数据存在多重共线性问题，另外考虑该地区数据样本量远小于变量个数，选择用偏最小二乘回归法。

4.2.2初步偏最小二乘回归及因字数确定

使用交叉验证原则(CV)判断偏最小二乘回归的成分数，将不同成分数对应的PRESS值及累计贡献率部分结果显示如下:

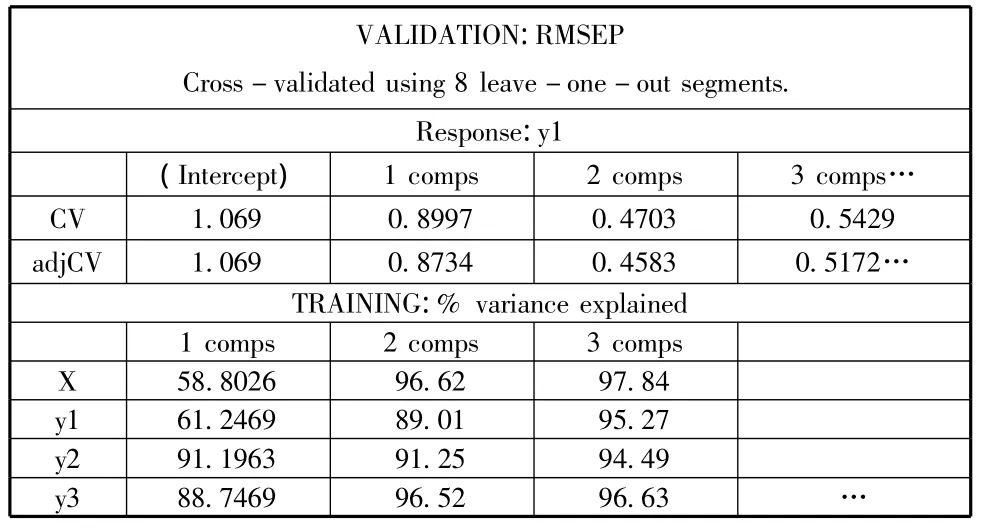
表6 发达省市初步偏最小二乘回归部分结果

根据上表我们可以看出，对于R＆D产出指标y1建模时，当因字数为2，PRESS=0.4703最小，且根据交叉验证的原理:在成分数尽可能小情况下，大部分因变量在因字数为2时PRESS值为最小。并且此时2个因子对各因变量的累计贡献率也都达到了90%，由此偏最小二乘回归改进模型的因字数m=2。

4.2.3改进模型

取因字数ncomp=2重新进行pls回归，并得到相应回归系数表:

表7 东部发达省市偏最小二乘回归系数表

根据上表，我们可以写出相应的各个回归方程(篇幅限制，此处略)。同时我们发现，与中西部发展省市相比，经济较发达省市的回归系数出现负值。例如针对出版科技著作种数，R＆D人员全时当量为负值，我们考虑到可能是由于经济发达地区人才聚集，科技投入饱和，导致人员溢出。另外由于著作主要是科研单位、高校在基础、应用研究方面的科技产出，该变量受企业、试验发展类科技投入负增长也是合理的。同样的新产品开发项目数主要是规上企业的科技产出，同理可解释该回归方程的负向系数。

4.2.4回归参数的显著性检验

使用R软件jack.test()函数检验回归参数的显著性，并将各回归系数对应的自变量显著情况整理如下表:

表8 东部发达省市R＆D投入指标显著性表

根据上表我们看出经济发达省市模型各变量显著性与发展地区明显不同:

①从执行部门来看，经济发达省市的R＆D总产出指标主要受企业R＆D人员及企业资金的影响最大，不太受政府资金影响，这主要是因为经济较发达省市的R＆D投入渐渐由大幅度增加科技投入量的粗放型，发展为更加注重经费来源的多元化并提高企业自主开发能力。对于大多数国家而言，由于科技发展的公共品性质导致科技发展初始阶段都依靠政府资金的投入来支持科技发展，但到发展的后期，会逐步转向依靠企业资金的投入，从这个角度来看，我们国家经济较为发达的地区也不例外。

②从研究领域来看，该地区总产出指标受试验发展方向的科技投入影响最显著。这主要因为经济发达省市更加注重科技成果的商品化与市场化，试验发展研究方向的科技成果与之更加吻合。

③对于论文、专著这类科技产出，政府资金对其的影响最大，不受企业资金的影响。研究机构、高校在基础、应用研究领域的科技产出大多为论文、专著形式，投入多、回报期限较长，大多企业不想投资，因此由政府承担起对基础研究的支持作用。

④对于规上工业企业的科技产出指标新产品开发项目数我们发现，它受政府资金及企业资金的双重影响都很显著，这主要是由于，这些地区虽然相对于本国其他地区经济发达，但我国科技投入的绝对水平与西方发达国家相比仍然偏低，我们虽然也要像发达国家那样鼓励企业提高科技创新意识，但政府也不能无限制降低科技投入比例，应该继续对企业的科技投入起引导作用。

4.2.5拟合效果分析

利用R软件我们绘出如下模型的拟合效果图，可以看出，虽然样本量较少，但散点大多集中在各因变量对角线区域，初步判定模型拟合效果较好。

图3 东部发达省市偏最小二乘回归拟合效果图

同样我们可以算出各因变量对应的R2值，由下表可以看出R2均达到83%以上，虽然样本数较少，但模型的拟合效果较好。

表9 发达省市模型拟合优度表

5. 小结

本文利用偏最小二乘法对中西部发展省市及东部经济较发达省市的R＆D投入-产出进行建模，该方法利用其独有信息筛选模式解决了自变量间的多重共线性问题，同时很好的解决了经济发达省市样本量少于变量的问题，两组模型的拟合优度都在80%以上，拟合效果较好，模型结果具有可参考性。

对于大多数国家而言，由于科技发展的公共品性质导致科技发展的初期阶段，资金来源主要依靠政府投入，而随着科学技术的应用程度的逐渐提高，企业资金投入在经济发达国家的科技投入中起着主要作用［7］。

通过分析我们发现:与国际上发展及发达国家科技投产机制的调整情况类似，对于我国中西部发展省市，R＆D人员全时当量及经费内部支出都对其R＆D科技产出有明显的促进作用，政府资金、企业资金对R＆D产出的影响都很显著，应该通过加大投入以获得更多的产出，同时在保证政府科技投入大幅度增加的前提下，引导企业、社会其他资源的投入，以科技创新带动当地经济发展。

对于东部经济较为发达的省市，企业R＆D人员全时当量及企业资金对R＆D科技产出指标的影响最显著，其次是其他资金，这主要是由于经济较为发达的省市，其R＆D投入已渐渐从原来的强调大幅度的科技投入量的粗放型，转变为多目标体系，通过改进投入机制，逐步形成政府、企业和社会共同发展的多渠道的科技投入体系。

［1］Griliches Z.Issues in Assessing the Contribution of R＆D to Productivity Growth ［J］.Bell Journal of Economics，1979，10(1):92-116.

［2］ Griliches Z.Market Value，R＆D，and Patents［J］.Economics Letters，1981，7(2):183-187.

［3］Hitt，Hosdisson，Johnson，Moesel.The market for corporate control and firm innovation ［J］.Academy of management journal，1996，39(5):1084-1119.

［4］Inonu E.The Influence of Cultural Factors on Scientific Production［J］.Scientometrics，2003，56(1):137-146.

［5］余昕，王冬，韩楠，王欣.发达国家科技投入效率初探［J］.科技进步与对策，2007(8):129-131.

［6］李燕萍，郭玮，黄霞.科研经费的有效使用特征及其影响因素［J］.科学研究，2009(11):1685-1691.

［7］华锦阳，汤丹.科技投入机制的国际比较及对我国科技政策的建议［J］.科技进步与对策，2010，27(5):25-30.

［8］吴喜之.复杂数据统计方法［M］.北京:中国人民大学出版社，2012:25-26.

［9］王惠文.偏最小二乘回归方法及应用［M］.北京:国防工业出版社，1999:151-152.

［10］齐琛，方秋莲.偏最小二乘建模在R软件中的实现及实证分析［J］.数学理论与应用，2013，33(2):104-105.

［11］ M iller R G.An unbalanced jackknife［J］.Ann Statist，1974，2:880-91.