给定顶点数和最大度的极大邻接谱双圈图
杨春燕,宋海洲
(华侨大学数学科学学院,福建泉州 362021)
给定顶点数和最大度的极大邻接谱双圈图
杨春燕,宋海洲
(华侨大学数学科学学院,福建泉州 362021)
通过对图进行收缩、夺邻、嫁接等运算,并利用Perron向量的一些性质,给出最大度为Δ(Δ≥3)的n(n≥5)阶极大邻接谱双圈图的一些性质,同时得到极大邻接谱双圈图的一些必要条件.
极大邻接谱双圈图;邻接谱;最大度;双圈图
本研究讨论有限且无向的~.设B=(V,E)是以V为顶点集、E为边集的~.用(u,v)或uv表示E中的一条边,其中u、v∈V;d(v)表示顶点v的度;Δ表示B中顶点的最大度;NB(v)表示B中所有与顶点v相邻的顶点构成的集合;设A为B的邻接矩阵,ρ(B)为B的邻接谱半径,若向量x=(x1,x2,…,xn)T满足‖x‖=1且Ax=ρ(B)x,则称x为B的Perron向量.
图的邻接谱是图谱理论的主要研究内容之一.文献[1]给出了图的邻接谱半径的图论意义.对于一个给定的图的集合,确定该集合中图的谱半径的上界,并刻画达到该上界的图,是Brualdi等[2]提出的关于图的谱半径的一个问题,此后这个问题被广泛研究.近年来关于双圈图的邻接谱半径的排序及分类问题的结果有很多.文献[3]给出了前三大邻接谱半径及它们对应的图;文献[4]进一步给出了第四大和第五大邻接谱半径及它们对应的图;文献[5]给出了第六大至第十大邻接谱半径及它们对应的图;文献[6]研究了给定权集的赋权双圈图的谱半径;文献[7]研究了给定围长和悬挂点数的双圈图的谱半径达到最大的极图的一些性质及极图的部分特征.本研究考虑最大度为Δ的n阶邻接谱双圈图集中极大邻接谱双圈图的性质.
1 一些定义和引理
定义1 设B*∈BΔn,若坌B∈BΔn,均有ρ(B)≤ρ(B*),则称B*为BΔn中的一个极大邻接谱双圈图.
定义2[4]设k≥2,v0,v1,…,vk为图中互不相同的顶点,若d(v0)≥3,d(vk)≥3,且对任意满足1≤i≤k-1的自然数i,均有d(vi)=2,则图B的一个路径v0v1…vk(k≥2)称为图B的一个内部路.
定义3 设B=(V,E)是n阶~,图B中度为1的点称为B的悬挂点,或称该点为B的叶子顶点.
定义4 设B是双圈图,C是B的一个圈.若导出子图B[V(C)]是一个单圈图,那么称C为B的基圈.
引理1[8]设B是简单连通图,x=(x1,x2,…,xn)T为B的Perron向量,xu、xv分别为顶点u、v对应的Perron向量的分量,wi∈NB(v){u},i=1,…,k.令B1=B-(v,w1)-(v,w2)-…-(v,wk)+(u,w1)+(u,w2)+…+(u,wk),若B1仍为简单连通图,且xu≥xv,则ρ(B1)>ρ(B).
引理2[8]设B=(V,E)是简单连通图,x=(x1, x2,…,xn)T为B的Perron向量,分别为4个互不相同的顶点u1、u2、v1、v2对应的Perron向量的分量,其中(u1,u2)、(v1,v2)∈E.令B1=B-(u1,u2)-(v1,v2)+(u1,v2)+(v1,u2),若B1仍为简单连通图,且xu1≥xv1,xu2<xv2,则ρ(B1)>ρ(B).
引理3[9]设B=(V,E)是简单连通图,v0v1…vk(k≥2)为B的一条内部路,若B1=B-(vi-1,vi)-(vi,vi+1)+(vi-1,vi+1)(1≤i≤k),则ρ(B1)≥ρ(B).
引理4[10]设B=(V,E)是连通图,u∈V(B),v埸V(B),B1=B+(u,v),则ρ(B1)>ρ(B).
①(v1,v3)∈E(B),(v2,v4)∈E(B),且(v1,v2)埸E(B),(v3,v4)埸E(B).
②(v1,v4)∈E(B),(v2,v3)∈E(B),且(v1,v2)埸E(B),(v3,v4)埸E(B).
证明 若①成立,令B1=B-(v1,v3)-(v2,v4)+(v1,v2)+(v3,v4),则易知.由xv1≥xv2≥xv3≥xv4,且xv1、xv2、xv3、xv4不全相等,有,由引理2知ρ(B1)>ρ(B).
若②成立,令B1=B-(v1,v4)-(v2,v3)+(v1,v2)+(v3,v4),则易知由不全相等,有不妨设由引理2知 ρ(B1)>ρ(B).
2 主要结果
引理6 设B*为中的极大邻接谱双圈图,x=(x1,x2,…,xn)T为B*的Perron向量,分别为v1、v2对应的Perron向量的分量.若d(v1)>d(v2),则
证明 用反证法证明.假设xv1≤xv2.记p=d(v1)-d(v2).由d(v1)>d(v2),知v1、v2至多有d(v2)个公共邻居,从而NB(*v1){NB(*v2)∪{v2}}中存在p个点vj2,…,vjp,使得
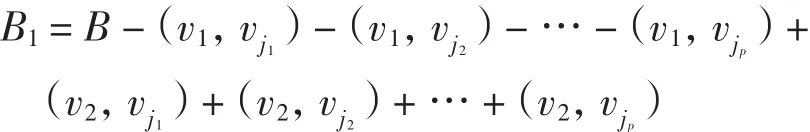
引理7 设B*是中的一个极大邻接谱双圈图,x=(x1,x2,…,xn)T为B*的Perron向量,则x的所有最大的分量对应顶点的度均等于Δ.
证明 用反证法证明.设v*∈V(B*),满足xv*=且d(v*)<Δ.记p=d(v*),任取V(B*)中度为Δ的一个顶点u,则p<Δ.由引理6知矛盾.故结论成立.
引理8 设B*是BΔn中的一个极大邻接谱双圈图,x=(x1,x2,…,xn)T为B*的Perron向量.若u*对应x中的分量xu*,满足,则u*在B*的圈上.
证明 用反证法证明.设v*∈V(B*),满足xv*=,点v*不在B*的任何一个圈上,由引理7可知d(v*)=Δ.这样,B*中就存在一条长为k的路v*v1…vk(k≥1),使得v*,v1,…,vk均不在B*的任何一个圈上,其中vk是叶子顶点,故d(vk)=1.对于B*的圈上任何一点u,有d(u)≥2>d(vk),由引理7得xvk<xu成立.
记v*为v0,设w是圈中离v*最近的顶点,在圈上任取2个异于w的相邻顶点u1、u2,即u1≠w,u2≠w,(u1,u2)∈E(B*),则有与xv0≥xu2成立.从而存在自然数l∈[1,k],使得如下2个不等式组中至少有1个成立:不妨假设自然数l0满足1≤l0≤k,及.令+则易知.由引理2有 ρ(B1)>ρ(B*),这与B*是BΔn中的一个极大邻接谱双圈图矛盾.故结论成立.
推论 设B*是BΔn中的一个极大邻接谱双圈图,x=(x1,x2,…,xn)T为B*的Perron向量,C为B*中的基圈,且V(C)={u1,u2,…,ul},xu1,xu2,…,xul分别为顶点u1,u2,…,ul对应的Perron向量的分量.若则l≤3.
证明 用反证法证明.假设l≥4.由引理7知d(u1)=d(u2)=…=d(ul)=Δ.不妨设u1,u2,…,ul在C上按顺时针排列.由B*是双圈图知u1、u2、ul-1,ul中存在一个点,它有邻居不在B*的圈上.不妨设u1的邻居v1不在B*的圈上,由引理7知.令 B1=B-(u1,v1)-(ul-1,ul)+(u1,ul-1)+(v1,ul),B1和B如图1所示,则易知由xu1=xu2=…=xul及可知又因为,由引理2有ρ(B1)>ρ(B*),这与B*是中的一个极大邻接谱双圈图矛盾.故假设不成立,从而结论成立.
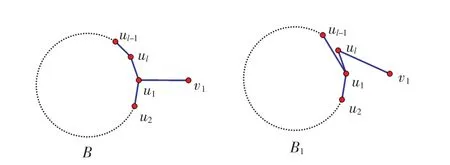
图1 B1和BFig.1 B1and B
引理9 设B∈BΔn,C是B中的基圈,V(C)={u1,u2,…,ul}(l≥4),且对任意满足1≤i≤l-1的自然数i,均有(ui,ui+1)∈E(B),且(ul,u1)∈E(B).若存在自然数i0∈[1,l],使得d(ui0)=2,则存在B1∈BΔn,使得ρ(B1)>ρ(B).
证明 用反证法证明.假设B为BΔn中的极大邻接谱双圈图.下面按C中度不小于3的点的个数分2种情形讨论.
情形1 V(C)中至少有2个顶点的度不小于3.
记ul+1=u1,则对任意满足1≤i≤l的自然数i,均有(ui,ui+1)∈E(B).由于存在i0∈[1,l],使得d(ui0)= 2,又V(C)中至少有2个点的度不小于3,可知存在满足m≥2且1≤t≤l-m+1的自然数m和t,使得utut+1…ut+m为B的内部路.令B1=(V(B1),E(B1)),其中:V(B1)=V(B){ut+1},E(B1)=E(B)-(ut,ut+1)-(ut+1,ut+2)+(ut,ut+2),易知B1∈BΔn-1,由引理3有ρ(B1)≥ρ(B).
若B有叶子顶点,取B中的任意一个叶子顶点v0,令B2=B1+(v0,ut+1),易知B2∈BΔn,由引理4可得ρ(B2)>ρ(B1),从而ρ(B2)>ρ(B),与假设矛盾.
若B无叶子顶点,取B1中度为2的顶点v1,令B3=B1+(v1,ut+1),易知B3∈BΔn.由引理4可得ρ(B3)>ρ(B1),从而ρ(B3)>ρ(B),与假设矛盾.
情形2 V(C)中仅有一个点的度不小于3.
此时,设uj是V(C)中唯一的度不小于3的顶点,为方便,将C上的点重新编号为V(C)={v1,v2,…,vl-1,uj},且v1,v2,…,vl-1,uj在C上按逆时针排列.由引理6可得
令B5=B-(vl-1,vl-2)+(vl-1,v1),则易知B5∈BΔn,由引理1有ρ(B5)>ρ(B),与假设矛盾.
综上可知假设不成立,故结论成立.
证明 因为对于任意满足1≤j≤l+1的自然数j,均有{uj,uj+1,…,uj+k-1}≠{r1,r2,…,rk},所以k≥2,故C上存在不同的2点v1、v2,且存在满足1≤i≤k,1≤s≤k及i<s的自然数i和s,使得v1介于ri与ri+1(顺时针)之间且与ri相邻,v2介于rs与rs+1(顺时针)之间且与rs相邻,并且有由r1,r2,…,rk的定义可知x令B1=B-B1和B如图2所示,则易知.因为由引理2有ρ(B1)>ρ(B),故定理结论成立.
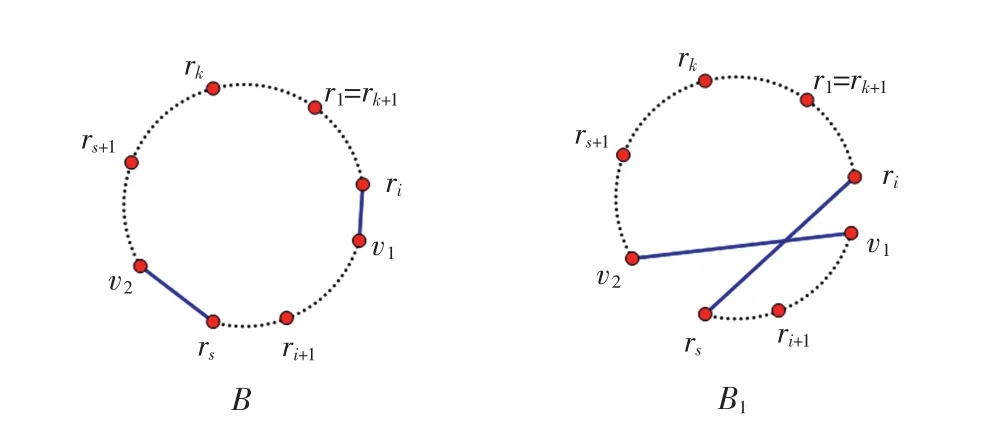
图2 B1和BFig.2 B1and B
[1]李乔,冯克勤.论图的最大特征根[J].应用数学学报,1979,2(2):167-175.
[2] BRUALDI R A,SOLHEIDE S.On the spectral radius of complementary acyclic matrices of zerosandones[J].SIAMJAlgebra DiscreteMethods,1986,7:265-272.
[3] HE C X,LIU Y,SHAO J Y.On the spectral radii of bicyclic graphs[J]. Journal of Mathematical Research and Exposition,2007,27(3):445-454.
[4]亓静.n阶双圈图的邻接谱半径[J].海南师范学院学报:自然科学版,2006,19(4):289-300.
[5] 王兴科,谭尚旺.双圈图按谱半径的排序[J].数学学报,2010,53(3):469-476.
[6]李丹,王国平.给定权集的赋权双圈图的谱半径[J].华东师范大学学报:自然科学版,2014(4):39-42.
[7]张梅.双圈图的特征值与结构参数[D].合肥:安徽大学,2010.
[8] BELARDO F,LI MARZI E M,SIMIC′S K,et al.On the spectral radius of unicyclic graphs with prescribed,degree sequence[J].Linear Algebra Application,2010,432(9):2323-2334.
[10]方坤夫.图的移接变换与谱半径大小的关系[J].湖州师范学院学报,2007,29(2):10-11.
(责任编校 马新光)
Maximal-adjacency-spectrum bicyclic graphs with given order and maximum degree
YANG Chunyan,SONG Haizhou
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,Fujian Province,China)
By using the operations of contracting,moving neighbors,grafting and the properties of Perron vector,the properties of the order n(n≥5)maximal-adjacency-spectrum bicyclic graphs with the maximum degree Δ(Δ≥3)are studied,and some necessary conditions about it are also obtained.
maximal-adjacency-spectrum bicyclic graphs;adjacency-spectrum;maximum degree;bicyclic graphs
1671-1114(2015)04-0016-04
O157.5
A
2014-12-17
华侨大学科研基金资助项目(10HZR26).
杨春燕(1992—),女,硕士研究生.
宋海洲(1971—),男,副教授,主要从事图论和组合优化方面的研究.

