基于Pareto最优的多目标集成柔性协作计划与分批调度

任晓青，张惠秋，包振强，汪 成，朱俊武

（扬州大学信息工程学院，江苏 扬州225127）

基于Pareto最优的多目标集成柔性协作计划与分批调度

任晓青，张惠秋，包振强*，汪 成，朱俊武

（扬州大学信息工程学院，江苏 扬州225127）

针对工件在实际批量生产模式下数量过多时其柔性协作计划、柔性批量分割和调度排序的集成优化难以进行同步决策的问题，构建了一种以平均交货期满意度、模糊总生产成本、模糊完工时间、平均拖期可信度等为目标的集成柔性协作计划与模糊柔性分批调度模型，设计了一种基于Pareto最优的多目标求解算法，并根据求解过程中的特殊性，提出了包括协作染色体、批量分割染色体和调度排序染色体的集成编码方案以及Pareto综合寻优方案，最后通过仿真结果验证了该方法的有效性.

多目标优化；柔性协作计划；模糊柔性分批；集成模型

多目标集成柔性协作计划［1-2］与柔性分批调度［3-4］问题是传统作业车间调度问题（iob-shop scheduling problem，JSP）的扩展，两者虽优于传统的调度方案，但其生产批次及工件的最佳数量难以确定，因此如何将柔性协作计划、柔性批量分割和调度排序进行同步决策并有效集成是解决该问题的关键.目前，关于批量生产的集成优化JSP研究较少.Jeong等［5］提出一种动态批量分批调度算法，但难以求解柔性JSP；Chan等［6-7］采用2种遗传算法独立优化工件的批量分割和调度排序；孙志峻等［8］采用等量分批策略同步优化各工件的子批数量和子批工件的加工排序，但仅限于等量分批，优化过程中各子批数量无法进行柔性调整；白俊杰等［9］提出一种基于“游标”的柔性批量分割法，但未考虑供应链背景下的协作计划与调度，且未将研究引入到更符合生产实际的模糊生产环境.本文同步考虑生产单元的内外部集成，在工件加工时间和交货期均服从模糊时间窗分布等约束的基础上，建立了一种多目标集成的柔性协作计划与模糊柔性分批调度模型，并设计出一种基于Pareto最优的多目标优化算法对目标模型进行优化求解.

1　模型建立

假设批量生产单元内有n个工件、m台机器，每个协作生产的工件被划分为p个子批，各子批作为一个整体处理，并共享同一批量启动时间.笔者选择平均交货期满意度、模糊总生产成本、模糊完工时间和平均拖期可信度4个常见性能指标［10］进行模糊度量［11］，并采用三角模糊数［12］代表模糊加工时间，梯形模糊数代表模糊交货期，模糊数的操作算子参见文献［13］.

1）平均交货期满意度：

2）总生产成本：

其中Pi为工件i的子批个数；qij为工件i在第j个批次中的数量；Yi为工件i的原材料成本；ni为工件i的工序数量；Ek为机器k在单位时间内的加工费用，k∈｛1，2，3，…，m｝；t′ijk为工件i的第j道工序在机器k上的模糊加工时间；dijk为决策变量，若工件i的第j道工序在机器k上加工，则dijk=1，否则dijk=0；Qi为工件i的生产批量数；ri为工件i的协作比例；Hi为工件i的协作成本.

3）完工时间：

其中Fi为工件i的模糊完工时间.

4）平均拖期可信度：

其中Bi为工件i的拖期可信度.

2　基于Pareto最优的多目标求解算法设计

2.1编码与解码

政府公共服务是由政府安排并生产的服务，即政府同时扮演了安排者和生产者的角色。公共服务体系中的基本参与者是消费者、生产者、提供者。[1]是政府满足社会公共需要，提供公共产品和社会服务的总称，其中公共服务的消费者是直接接受服务的个人、组织、社会等；公共服务的生产者——政府、私企、非营利机构等直接向消费者提供服务。政府作为公共服务的提供者，指派生产者给消费者，或者反之，对公共服务的供应承担着重要的责任。所以政府公共服务就是政府在公共服务体系中承担生产和供给的职责。[2]

本文设计了3个部分染色体：1）协作染色体.表示对应工件的协作比例，以0～1之间的随机数计，并规定当工件只有很少一部分须自行或协作加工时则相应地完全自行或协作加工；2）批量分割染色体.表示各工件的批量分割策略，采用基于“游标”的柔性批量分割的方法；3）调度排序染色体.表示各批次的调度排序，采用基于工序的编码方式.编码时，各染色体间以“00”间隔，如图1所示.

图1　染色体编码方案Fig.1 Chromosome coding scheme

分别对三部分染色体进行解码得调度方案，进而得到问题的一个可行解.由图1可见，若有2种不同类型的工件，生产数量均为10，其协作染色体的协作比例为0，0.4，表明需要自行加工的数量分别为10，6；批量分割染色体部分“37”“2”表示2种工件分别通过游标被分为3（3，4，3），2（2，4）批；调度排序染色体中“12-4”表示第1种工件的第2个子批次在机器4上加工，首次出现的“11”表示工件1第1个批次的第1道工序，第2次出现的“11”表示工件1第1个批次的第2道工序，依此类推.

2.2交叉与变异

由于交叉或变异过程中各种工件的批次数量可能发生变化，故应根据批次数量的变化增加或减少染色体后一部分的长度.鉴于此特殊性，整个染色体的交叉和变异过程如下.

1）协作染色体.选择如图2所示的单点交叉策略，采用随机位随机变异.

图2　协作染色体交叉示例图Fig.2 Collaboration chromosome

2）批量分割染色体.交叉的基因个数随机，每种工件的加工数量不一定相同，交叉后若游标超出工件的实际加工数量，则去掉超出部分的游标；若批次增加，则在染色体后一部分任意位置随机插入相应的染色体，反之，则删除多余的染色体，如图3所示.采用随机交换2个基因的方法进行变异，并以相同的方法修复产生的非法染色体.

图3　批量分割染色体交叉、修复示意图Fig.3 Lot-splitting chromosome

3）调度排序染色体.父代染色体的批量分割染色体部分相同，调度染色体才能进行交叉，交叉方法及变异操作与批量分割染色体部分类似.

2.3快速非支配排序与选择操作

采用基于Pareto最优的非支配排序方法，结合小生境技术中的拥挤距离来维持群体分布的多样性.经过非支配排序和拥挤距离的计算，得到每个个体的非支配等级ri和拥挤距离Li.定义一种偏序关系≻n为i≻nj，如果ri＜rj或ri=rj且Li＞Lj，则解i优于解j.基于这种偏序关系进行选择操作，当个体等级和拥挤距离均相等时，则应根据决策者偏好优先选择重要指标较好的个体.

2.4算法流程

1）随机产生初始种群P0，种群规模为P，并设t=0；

2）对P0进行非支配排序并计算拥挤距离，然后通过选择、交叉和变异操作产生第一代子代种群Q0；

3）合并父代种群和子代种群Rt=Pt∪Qt，对Rt进行非支配等级排序，按照Pareto概念构造非支配等级曲面F，F=｛F1，F2，…，Fi｝，其中Fi是等级i的非支配曲面；

4）清空Pt+1，并设i=1；

5）如果|Pt+1|+|Fi|≤P，则继续步骤6），否则跳至步骤8）；

6）计算Fi中染色体的拥挤距离，并将Fi中的个体加入子代种群Pt+1，Pt+1=Pt+1∪Fi；

7）令i=i+1，返回步骤5）；

8）对Pt+1执行选择、交叉以及变异操作，产生新的种群Qt+1；

9）如果t＜Gmax（最大进化代数），则t=t+1，返回步骤3）；否则算法终止.

3　仿真结果分析

本文算法以Java编程语言实现，程序运行环境为P4 CPU，主频2.8 GHz，内存1.25 GB.算法参数设置如下：种群规模P=100，交叉概率Pc=0.45，变异概率Pm=0.05，最大进化代数Gmax=80，可信度系数λ=0.5，其他参数略.仿真数据如表1～3所示.

程序运行后所得部分具有代表性的Pareto优化解集如表4所示.同时，在相同条件下，采用本文设计的算法对传统协作计划和不分批调度问题进行优化求解，结果如表5所示.

由表4～5可知，柔性协作计划与柔性分批调度的组合优化更能有效地均衡生产单元自身的产能，提高机器利用率，缩短生产周期，增强交货期满意度，降低制造成本.

表1　工件对应的可加工机器Tab.1　Corresponding machines of each job

表2　工件的生产加工数据Tab.2 Associated production data of each job

表3　各机器的单位时间加工费用Tab.3 Processing cost per unit time of each machine

表4　柔性协作计划、柔性分批优化调度Pareto解集Tab.4 The Pareto optimal solution of integration of flexible collaborative planning and flexible lot-splitting scheduling

表5　传统协作计划、不分批调度Pareto解集Tab.5 The Pareto optimal solution of integration of collaborative planning and scheduling

本文选取表4中第3个解作为最终调度方案，在该方案中，各工件的协作比例为0.5，1，0，0.8，0.4，0.2，其中第3，5，6种工件分别分为2（3，7），2（3，3），2（3，5）个子批，其他工件不分批，共8个子批量，对应的调度甘特图如图4所示（图中数字表示工件种类、批次及对应工序，如“3，2-1”表示第3种工件的第2个批次的第1道工序）.通过图4可以清晰地反映每个工件的每个批次中各工序所对应的加工顺序及其加工机器，同时也能快速反映出工件的最终完工时间.

［1］BAO Zhenqiang，WANG Guiiun，BAO Rong，et al.A novel hybrid evolutionary algorithm for the integrated model of collaborative planning and scheduling with tasks dividable［J］.J Comput Inf Syst，2010，6（12）：4099-4108.

［2］包融，王伟业，顾汉杰，等.订单可分的协作计划模型及其进化算法［J］.计算机技术与发展，2010，20（10）：58-61.

［3］LOW C Y，HSU C M，HUANG K I.Benefits of lot splitting in iob-shop scheduling［J］.Int J Adv Manuf Technol，2004，24（9/10）：773-780.

［4］潘全科，朱剑英.多工艺路线的批量生产调度优化［J］.机械工程学报，2004，40（4）：36-39.

［5］JEONG H I，PARK J，LEACHMAN R C.Batch splitting method for a iob shop scheduling problem in an MRP environment［J］.Int J Prod Res，1999，37（15）：3583-3598.

［6］CHAN F T S，WONG T C，CHAN P L Y.Equal size lot streaming to iob-shop scheduling problem using genetic algorithms［C］//Proceedings of 2004 IEEE International Symposium on Intelligent Control.Taipei：IEEE，2004：472-476.

［7］CHAN F T S，WONG T C，CHAN L Y.Lot splitting under different iob shop conditions［C］//Proceedings of 2007 IEEE Congress on Evolutionary Computation.Washington D C，USA：IEEE，2007：4722-4728.

［8］孙志峻，安进，黄卫清.作业车间多工艺路线批量作业计划优化［J］.中国机械工程，2008，19（2）：183-187.

［9］白俊杰，龚毅光，王宁生，等.多目标柔性作业车间分批优化调度［J］.计算机集成制造系统，2010，16（2）：396-403.

［10］BEHNAMIAN J，FATEMI GHOMI S M T.Multi-obiective fuzzy multiprocessor flowshop scheduling［J］. Appl Soft Comput J，2014，21：139-148.

［11］杨宏兵，严洪森，陈琳.知识化制造环境下模糊调度模型和算法［J］.计算机集成制造系统，2009，15（7）：1374-1382.

［12］LV Zehua，JIN Hai，YUAN Pingpeng.The theory of triangle type-2 fuzzy sets［C］//Proceedings of IEEE 9th International Conference on Computer and Information Technology.United States：IEEE，2009：57-62.

［13］SAKAWA M，KUBOTA R.Fuzzy programming for multiobiective iob shop scheduling with fuzzy processing time and fuzzy duedate through genetic algorithms［J］.Eur J Opera Res，2000，120（2）：393-407.

Multi-objective integration of flexible collaborative planning and fuzzy flexible lot-splitting scheduling based on the Pareto optimal

REN Xiaoqing，ZHANG Huiqiu，BAO Zhenqiang*，WANG Cheng，ZHU Junwu
（Sch of Inf Engin，Yangzhou Univ，Yangzhou 225127，China）

It is difficult to optimize the flexible collaborative planning，the flexible lot splitting and scheduling of the iob simultaneously in batch production mode，a model for multi-obiective integration of flexible collaborative planning and fuzzy lot-splitting scheduling is established.The author takes four performance indicators to optimize the model：average delivery satisfaction，fuzzy total cost，fuzzy completion time and average credibility of iob tardiness，and establishes a multi-obiective algorithm based on the Pareto optimal.In this algorithm，the integrated coding scheme is designed，which includes collaboration chromosome，lot-splitting chromosome and scheduling chromosome，meanwhile the Pareto optimal scheme is also designed.Finally，the efficiency of the model and algorithm is proved by simulation.

multi-obiective optimization；flexible collaborative planning；fuzzy flexible lot splitting；integrated model

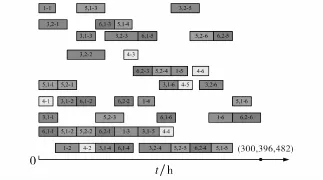
图4　柔性协作计划、柔性分批优化调度甘特图Fig.4 Gantt for integration of flexible collaborative planning and flexible lot-splitting scheduling

TP 181；TP 301.6

A

1007-824X（2015）01-0036-05

（责任编辑 林 子）

2014-02-25.*联系人，E-mail：yzbzq@163.com.

国家自然科学基金资助项目（61170201）；江苏省研究生科研创新项目（CXZZ13_0919）.

任晓青，张惠秋，包振强，等.基于Pareto最优的多目标集成柔性协作计划与分批调度［J］.扬州大学学报：自然科学版，2015，18（1）：36-40.