板与柱半刚接－防屈曲钢板墙简化计算模型分析

杜文学， 朱文波， 李长凤， 唐洪堃

(黑龙江科技大学 建筑工程学院，哈尔滨 150022)

0 引言

目前，组合钢板剪力墙是新建结构和加固改造中所广泛采用的抗侧力构件，在新型钢结构体系中，由于其抗剪强度高、整体性强、能够很好的防止板的平面外屈曲，所以在一些高层建筑结构中得到了广泛应用。国内外学者对组合钢板剪力墙开展了大量的研究[1－4]，众多研究发现，在加载后期混凝土墙板与周边框架、混凝土与销钉均会相互挤压，当混凝土被压碎脱落后，就不能很好的抑制钢板在平面外屈曲。针对这一缺陷，研究者们在寻求一种能够改善钢板剪力墙屈曲约束的构造，来改善组合钢板剪力墙的受力性能。我国学者郭彦林等提出了防屈曲钢板墙[5－7]。即在两侧盖板和内嵌钢板的相同位置开孔以便螺栓穿过，两侧盖板预留孔径略大于螺栓杆直径，通过混凝土盖板和内嵌钢板接触面之间相互错动的机制，可避免混凝土盖板破坏，为钢板提供持续稳定的平面外支撑。

然而，在大震时，钢板与混凝土板可发生相互的错动，此时板内形成的拉力带会对边柱产生附加弯矩的作用[8－11]，柱子过早发生压屈，影响结构整体的承载力。国内外对防屈曲钢板墙板与柱连接特性的研究文献尚未见报道。为了减弱板对边柱造成的拉力，笔者提出板与柱半刚性连接，在组合钢板墙简化模型的基础上，给出相应的弱拉杆简化计算模型。采用有限元程序对板与柱刚接、板与柱半刚接防屈曲进行模拟分析，考察不同边柱刚度系数对两种防屈曲钢板墙承载力的影响。

1 模型的建立

在组合钢板墙的受拉条带模型中，拉力杆不仅形成于上梁与下梁之间，而且形成于梁柱之间。针对提出的板与柱半刚接构造，需减弱梁柱之间形成的拉力杆。组合钢板墙的受拉条带模型中，假设边柱刚度足够大，不足之处是缺乏拉杆对边柱造成的实际影响，若边柱先于结构整体破坏时，需考虑边柱的刚度因素对结构承载力的影响。

1.1 组合钢板墙受拉条带总剪力

文献[12]中对组合钢板剪力墙的简化模型提出了三点假设，即:假设梁柱铰接，梁柱刚度足够大，每根拉杆在侧向位移为x时的应力相同。在侧向位移为x时，由组合钢板墙简化的拉杆模型算得的拉杆应力为

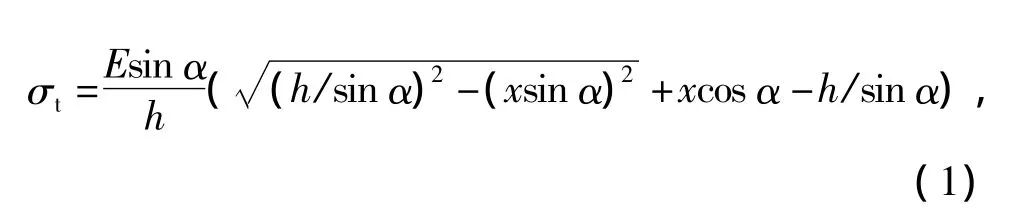
式中:h—— 钢板高，mm;

E—— 弹性模量，MPa;

x——横向位移，mm;

α—— 受拉条带倾角，(°)。受拉条带所受的总剪力为

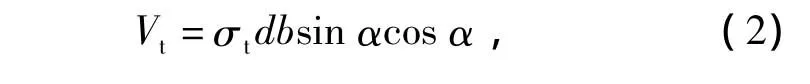
式中:d—— 钢板厚，mm;

b —— 钢板宽，mm;

σt——受拉条带应力，MPa。

把式(1)代入式(2)，可得受拉条带总剪力Vt与侧移量x之间的关系式。

1.2 弱拉杆模型总剪力

上述假设中把柱的刚度视为足够大，未考虑板内形成的拉力带对边柱造成的附加弯矩作用。文中以组合钢板墙的拉力条带模型为基础，针对板与柱半刚接－防曲屈钢板墙提出弱拉杆模型，同时考虑柱刚度系数的影响。半刚接单元模型见图1，耳板与边柱采用焊接，与钢板采用螺栓连接，耳板中预留孔径略大于螺栓杆直径。在加载过程中，通过耳板和内嵌钢板之间相互错动，以减弱对边柱拉力作用，避免边柱过早发生压屈破坏，形成一种良好的耗能机制。

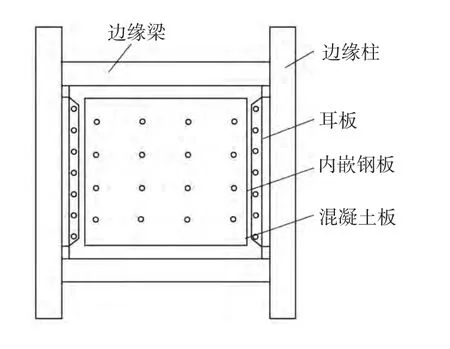
图1 结构单元Fig.1 Structural unit

对于弱拉杆模型，假设梁柱铰接、每根拉杆在侧向位移为x时的应力值相同。图1所对应的弱拉杆条带模型如图2所示，在侧向位移为x下，受拉条带所受的总剪力为Vt。图2中实线为上下梁形成的简化拉杆，虚线为弱拉杆，形成于梁柱之间。

弱拉杆的应力为σλ，由于板与柱半刚接，在侧向位移为x时，弱拉杆的应力要小于实拉杆的应力，弱拉杆的应力可以通过实拉杆的应力乘以一个折减系数λ，即

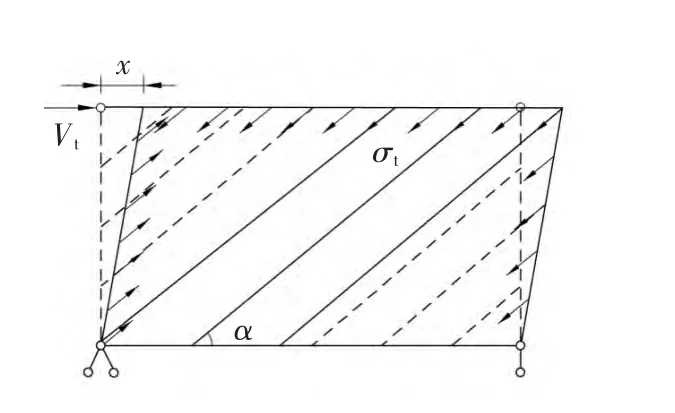
图2 侧移量为x时的拉杆应力Fig.2 Stress of pull rod when lateral displacement is x

弱拉杆模型的总剪力为实拉杆所受的总剪力与弱拉杆所受总剪力之和

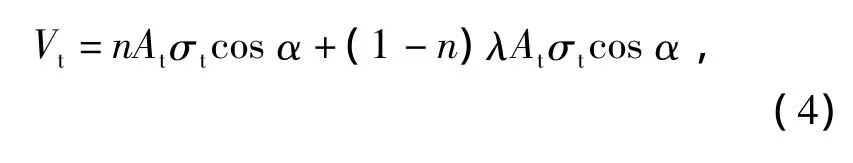
式中:n——实拉杆占总拉杆的比例;

At—— 受拉条带截面积，mm2。

把式(1)、(3)代入式(4)中，可以得到总剪力与侧移x的关系式。由式(4)与式(2)对比可以发现，弱拉杆模型减弱了对柱子造成的拉力，同时也减弱钢板墙的承载力。减弱值为

式中:ΔV—— 钢板总剪力的减小值。

1.3 边柱因素对结构承载力的影响

需注意的是，式(4)中获得的总剪力并没有考虑柱的刚度因素，若考虑其影响可分三种情况，即边柱先于整体破坏，整体先于边柱破坏，二者同时达到破坏。考虑边柱刚度对结构承载力的影响。侧移量为x时，根据每根拉杆对柱底造成的附加弯矩，可得到柱底的附加弯矩

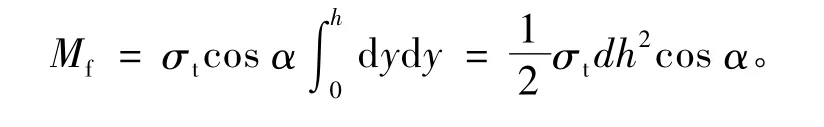
柱底受到的附加应力为

式中:σf—— 柱底附加应力，MPa;

数字音乐，通常包括电影、影视剧、游戏、动漫音乐等，是当今社会发展迅猛的新兴领域。它是用数字格式通过互联网存储和传输音乐，人们通过电脑、手机等媒介，进行下载等。[2]既是互联网、计算机等手段播放音乐的总称，也是音乐与网络技术相融合的产物。随互联网的发展，由于数字音乐拥有方便、快捷等特点，占据音乐产业的半壁江山。从全球音乐产业的发展格局变迁看，音乐产业正在实现从实体音乐向数字音乐的转型。因而，音乐产业迎来新的发展机遇。

Mf—— 柱子受到的附加弯矩，N·m;

W—— 柱截面形常数，cm3。

柱底受到的最大正应力为

式中:n—— 轴压比;

σy—— 边柱屈服应力，MPa。

柱的最大正应力可以根据柱子的材料或是自行设定设计值，则附加应力

将式(7)代入式(6)中，可得拉条带能承受的应力

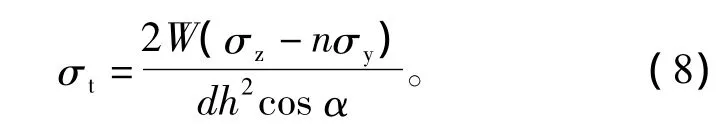
将式(8)代入式(1)中，可得柱子可承受的应力值与位移量x之间的关系式:

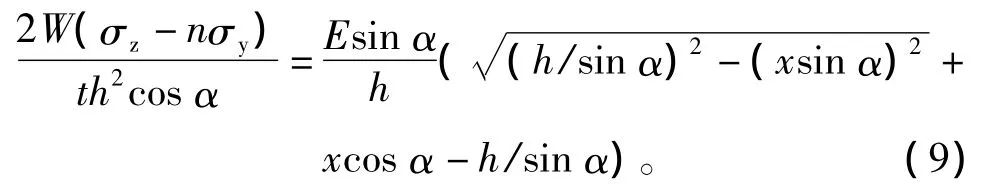
当柱刚度足够大，受拉条带的总剪力可以采用式(2)算得;若柱刚度较弱，柱子压屈先于结构整体破坏时，需考虑柱子的刚度因素。受拉条带总剪力应采用式(10)算得

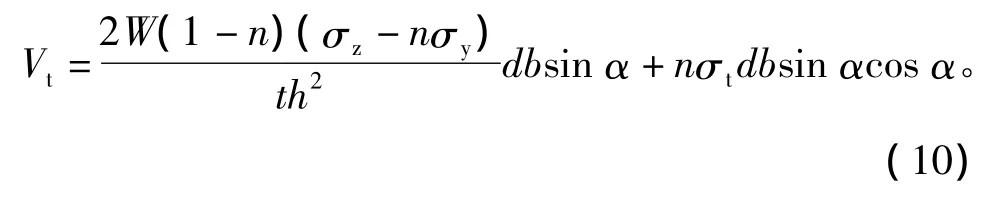
若采用弱拉杆模型，此时边柱尚未达到压屈破坏，当弱拉杆模型边柱达到破坏时，结构整体侧移有所增加，当侧移增量为Δx时，拉杆应力增量为

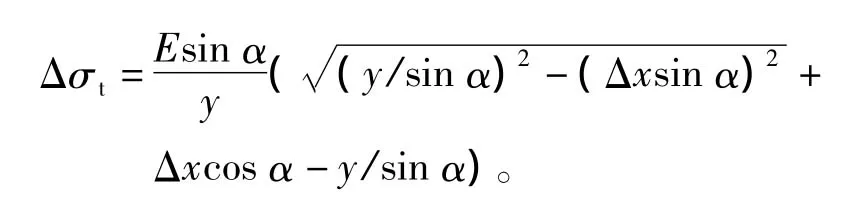
当侧移增量为Δx时，钢板剪力增量值为

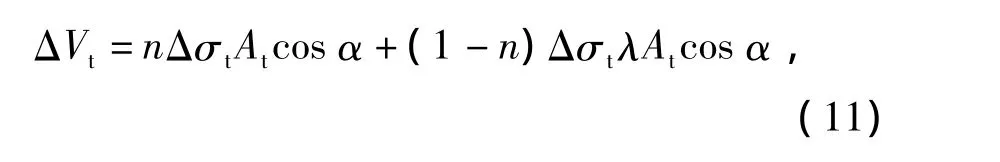
弱拉杆模型总剪力增加值为弱拉杆减弱值ΔV与钢板剪力增加值ΔVt之和。

2 模拟分析

2.1 有限元模型

防屈曲钢板墙数值分析中，钢材均采用带强化段的三折线本构模型，E=2.06×105MPa，fy=235 MPa，εy=0.001 14，强化初应变 εst=0.02，强化切线模量Et=0.03E。混凝土强度等级为C30。梁、柱和混凝土板采用实体单元(C3D8)，钢板采用一般壳单元(S4R)，板与梁、梁与柱采用绑定约束，混凝土板采用约束自由度的方法，约束z方向的自由度，实现约束钢板的面外屈曲。模型尺寸如表1所示。

表1 构件截面Table 1 Member section mm

在模拟中通过改变板的高度来改变高宽比，改变柱的截面尺寸来改变柱刚度系数，柱刚度系数见表2。

表2 柱刚度系数β取值Table 2 Column stiffness coefficient of β values

2.2 荷载-位移曲线

荷载－位移见图3。

图3 荷载-位移曲线Fig.3 Load-displacement curves

由图3a可知，在高宽比a为0.5时，板与柱刚接比板与柱半刚接防屈曲钢板墙的极限荷载值高2%左右。由此可见，在低高宽比下板与柱半刚接并不能提高结构的承载力;如图3b所示，在高宽比为1.0时，板与柱半刚接比板与柱刚接防屈曲钢板墙的极限荷载值高3%左右。由此可见，在高宽比为1.0时，板与柱半刚接不仅可以提高结构的延性而且可以提高结构的承载力。

2.3 应力分布

图4为1/50侧移角下结构的应力分布。

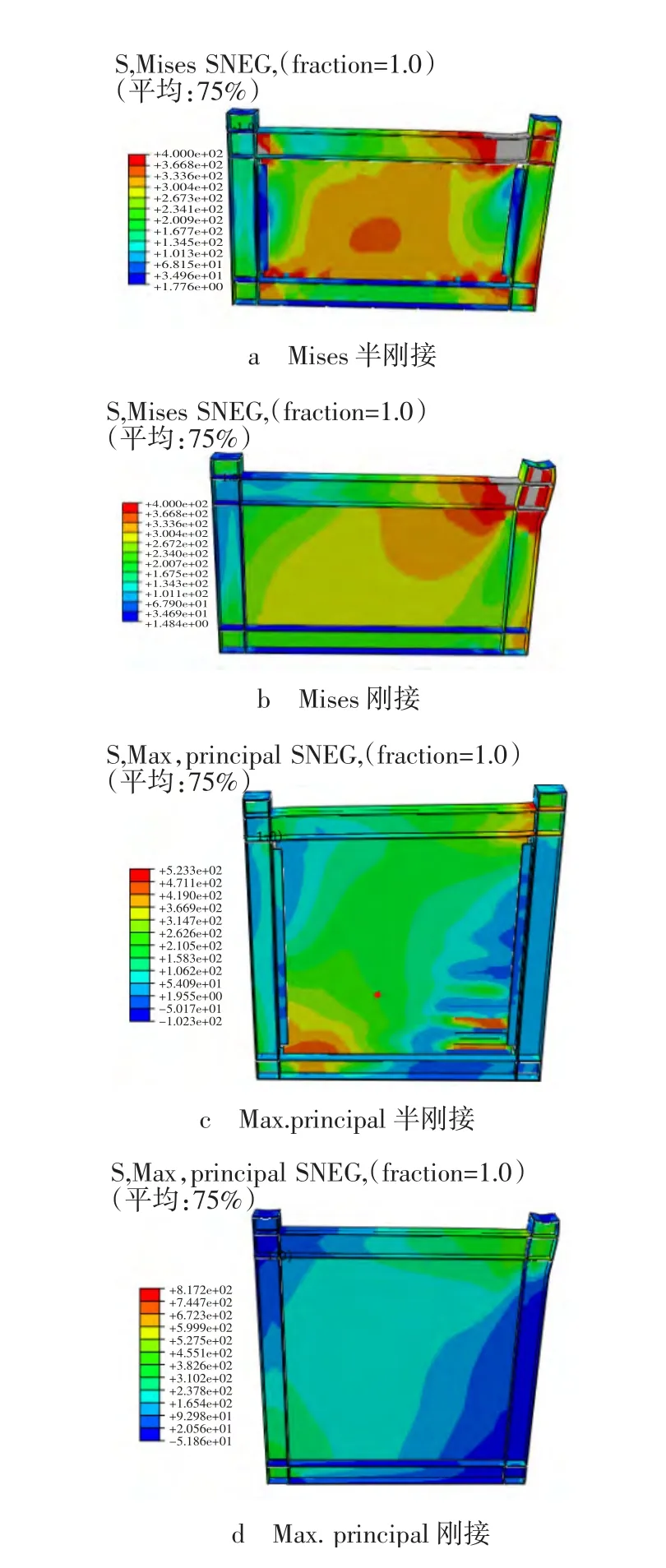
图4 应力分布Fig.4 Stress distribution

如图4a、b所示，当板与柱采用半刚性连接时，耳板对钢板的约束作用较弱，钢板内的对拉带主要形成于上下梁之间，板边的应力要远小于板中的应力，在这里弱拉杆模型得到了很好的体现。不难看出，在低高宽比下板与柱采用刚接，防曲屈钢板墙整体性好，应力主要分布在钢板的对角区域，板对边柱有明显拉力作用。当在高宽比为1.0时，两种钢板墙的应力分布如图4c、d所示，半刚接板在加载后期板内对拉带主要形成于板的对角线区域，板角出现压屈现象，由于板与柱采用半刚性连接，板对柱子的拉力减弱，柱的应力远小于板与柱刚接中柱的应力。

3 理论分析

假设拉力条带的倾斜角为45°，在高宽比为0.5时，弱拉杆与实拉杆各占一半;高宽比为1.0时，拉杆全部折减，折减系数取0.8。柱子轴压比取0。把以上数据代入式(9)，通过改变柱刚度系数，考察不同柱刚度系数下，随侧移量的增加，拉力杆对柱底造成的附加应力值。随侧移量的增加，板内形成的拉杆对边柱造成的附加应力不断增大，在1/50侧移角下限值内，若附加应力值达到材料屈服强度值时，则需考虑柱刚度系数对结构承载力的影响。把拉杆应力代入式(3)，得到减弱后的拉杆应力值。此时，钢板墙承载力减弱值为式(5)。继续增加侧移量，当附加应力再次达到屈服强度值时，记录侧移增量值Δx。把Δx代入式(11)，得到钢板墙承载力的增量值。

侧移量x对应柱底附加应力σf如表3所示。表3可以看出，在高宽比为0.5时，1/50侧移角下，刚接、半刚接柱底的附加应力均未达到材料的屈服强度，半刚接的屈服荷载、极限荷载比刚接均降低了2%。可见在低高宽比下，弱拉杆模型可以提高结构延性，但会降低结构的承载力。在高宽比为1.0、柱刚度系数为22.17、侧移量为20 mm时，柱底达到屈服强度;侧移量为26 mm时，柱底应力达到极限强度。减弱后柱低屈服强度的侧移量增加了6 mm，极限强度侧移量增加了7 mm。柱刚度系数为35.11、侧移量为36 mm时，柱底达到屈服强度;侧移量为47 mm时，柱底达到极限强度。减弱后柱低屈服强度的侧移量增加了10 mm。柱子刚度系数为50.88时，柱子刚度柱足够大，可以抵抗板内形成的拉力带对柱子造成的附加弯矩作用。在侧移量为60 mm时，柱底的附加应力未达到材料的屈服强度值。

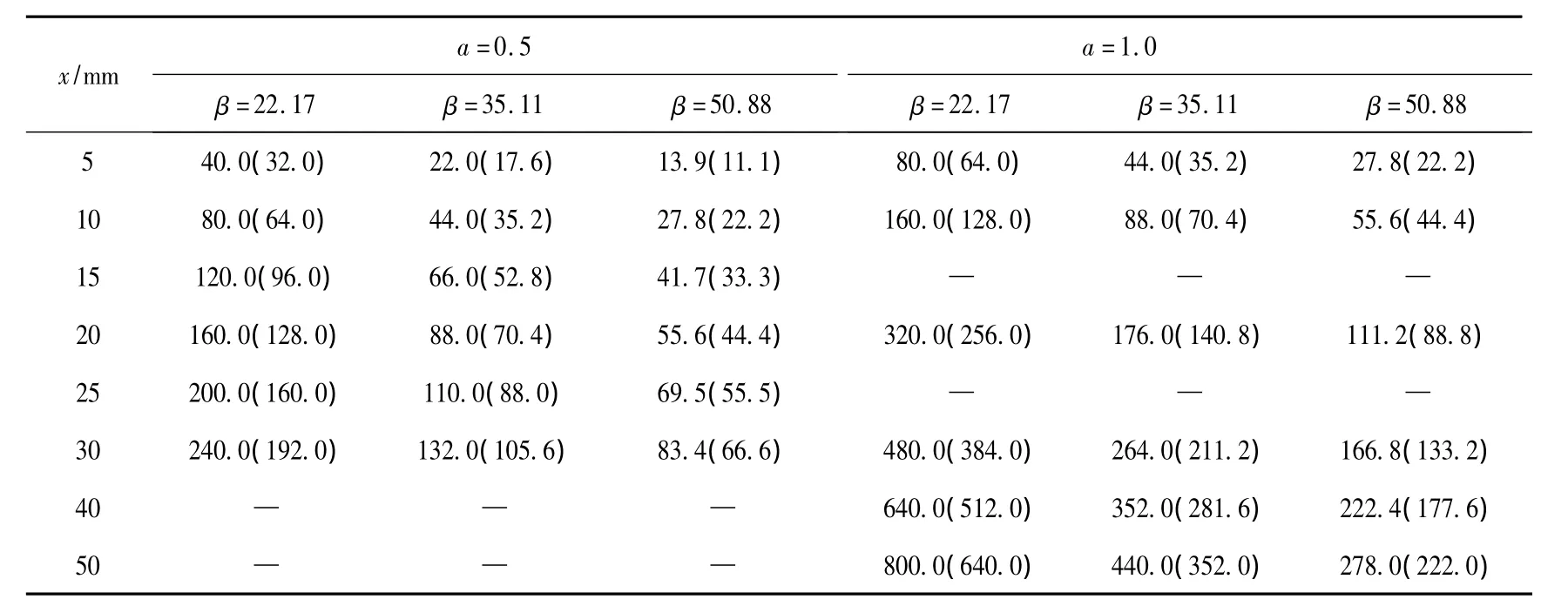
表3 侧移量对应柱底附加应力Table 3 Low added value of column corresponding lateral displacement MPa

当高宽比为1.0、β=22.17、侧移量达到20 mm时，柱子发生屈服，采用弱拉杆模型后，减弱后柱低屈服应力对应的侧移量增加了6 mm。侧移量增加6 mm后，按式(5)算得的弱拉杆减弱值为2 295 kN，按式(11)算得的钢板剪力增加值为2 475 kN，弱拉杆模型总剪力增加值为180 kN。增加量约为原剪力值的2%;当β=35.11，在侧移量达到36 mm时，柱子发生屈服，采用弱拉杆模型时，减弱后柱底屈服应力对应的侧移量增加了10 mm。侧移量增加了10 mm后，按式(5)算得的弱拉杆减弱值为2 240 kN，按式(11)算得的钢板剪力增加值为3 250 kN，弱拉杆模型总剪力增加值为1 010 kN。增加量约为原剪力值的2%。

由上述理论与模拟分析可知，在高宽比为1.0、柱子刚度系数为22.17、35.11时，侧移量分别增加6、10 mm，弱拉杆模型总剪力分别增加180、1 010 kN。减弱的拉杆模型不仅可以提高结构的延性，同时可以提高结构的承载力。

4 结论

(1)通过模拟分析与理论分析，考虑到板与边柱半刚性连接，同时考虑柱刚度系数因素，验证了弱拉杆模型的可行性。

(2)随着柱刚度系数的增加，板内形成的拉力带对柱子造成的附加弯矩越弱。当柱刚度足够大时，可不考虑柱刚度因素对钢板墙承载力的影响。

(3)当高宽比1.0，边柱刚度系数为22.17，侧移量为20 mm，刚度系数为35.11，侧移量为36 mm时，边柱均发生屈服。采用半刚性连接，边柱的屈服位移分别提高了6和10 mm。

(4)在高宽比为0.5时，板与柱半刚接可以改善结构的延性，但会降低结构的承载力，降低值约为2%;在高宽比为1.0时，半刚接板比刚接板极限承载力提高约为3%。

(5)在侧向位移相同时，板与柱半刚接减弱了对边柱的拉力作用，同时也减弱了钢板的侧向承载力，当弱化拉杆模型的边柱达到屈服强度时，半刚接比刚接板的侧移量有所增加，此时结构承载力的增量取决于钢板的增量值与弱拉杆的减弱值。

[1]高 辉.组合钢板剪力墙试验研究与理论分析[D].上海:同济大学，2007.

[2]滕 跃，彭晓彤.组合钢板剪力墙结构动力时程分析[J].济南大学学报:自然科学版，2015，29(3):23－29.

[3]陈 麟，赵锐荣，周 云.钢板墙与防屈曲组合钢板墙的受剪性能分析[J].建筑科学，2011，27(7):15－21.

[4]孙飞飞，刘桂然.组合钢板剪力墙的简化模型[J].同济大学学报:自然科学版，2010，35(1):18－23.

[5]郭彦林，周 明.非加劲与防屈曲钢板剪力墙性能及设计理论的研究现状[J].建筑结构学报，2011，32(1):1－16.

[6]郭彦林，董全利，周 明.防屈曲钢板剪力墙弹性性能及混凝土盖板约束刚度研究[J].建筑结构学报，2009，30(1):40－46.

[7]郭彦林，董全利，周 明.防屈曲钢板剪力墙滞回性能理论与试验研究[J].建筑结构学报，2009，30(1):31－39.

[8]XUE M，LU L W.Interaction of infilled steel shear wall panels with surrounding frame members[C]//Proceedings，1994 Annual Task Group Technical Session，Structural Stability Research Council:reports on current research activities.Bethlehem:Lehigh University，1994:339－345.

[9]XUE M，LU L W.Monotonic and cyclic behavior of in filled steel shear panels[C]//The 17th Czech and Slovak International Conference on Steel Structures and Bridges.Bratislava，Slovakia:[s.n.]，1994:152 －160.

[10]VIAN D，BRUNEAU M，TSAI K，et al.Special perforated steel plate shear walls with reduced beam section anchor beamⅠ:Experimental Investigation[J].Journal of Structural Engineering，2009，135(3):211－220.

[11]VIAN D，BRUNEAU M，TSAI K，et al.Special perforated steel plate shear walls with reduced beam section anchor beamⅡ:A-nalysis and Design Recommendations[J].Journal of Structural Engineering，2009，135(3):221－228.

[12]孙飞飞，戴成华，高 辉.四边连接组合钢板剪力墙的简化模型[J].同济大学学报:自然科学版，2009，37(7):8－14.