基于改进集的集值Ekeland变分原理
万轩,张万里,赵克全
(1.重庆电讯职业学院基础部,重庆402247;2.重庆师范大学数学学院,重庆401331)
基于改进集的集值Ekeland变分原理
万轩1,张万里2,赵克全2
(1.重庆电讯职业学院基础部,重庆402247;2.重庆师范大学数学学院,重庆401331)
Ekeland变分原理在最优化理论及应用研究中具有十分重要的作用.利用非线性标量化函数及相应的非凸分离定理建立了基于改进集的集值Ekeland变分原理.新的Ekeland变分原理包含了一些经典的Ekeland变分原理作为其特例.
改进集;Ekeland变分原理;集值映射;非线性标量化函数
1 引言
众所周知,经典的Ekeland变分原理在最优化理论及应用,控制理论和非线性分析等很多领域中都具有十分广泛的应用[1-2].近年来,许多学者对经典的Ekeland变分原理进行了深入研究,获得了一系列具有重要理论意义与价值的研究成果[3-9].特别地,文献[3]分别基于完备序空间和完备度量空间建立了广义集值Ekeland变分原理.文献[4]建立了局部凸空间中的一类变形的集值Ekeland变分原理,即Ha型集值Ekeland变分原理,并研究了这类集值Ekeland变分原理的稳定性.文献[5]基于完备度量空间利用集值度量等概念对向量值Ekeland变分原理进行推广,得出了一类新的带集值度量的Ekeland变分原理.随后,Guti´errez等人又在文献[6]中基于度量空间(不必完备)利用一类近似解建立了一类集值Ekeland变分原理.此外,文献[8]对文献[4]中所建立的Ha型集值Ekeland变分原理进行了推广,并建立了相应的等价性结果.文献[9]中利用集值拟度量进一步推广了文献[5]中获得的主要结果,建立了集值拟度量的集值Ekeland变分原理,并由此获得了向量优化问题近似解的一些相关研究结果.
文献[10]基于comprehensive集提出了有限维空间中改进集的概念,并研究了改进集的一些拓扑性质.文献[11]将改进集及E-有效解概念推广到了一般实分离局部凸拓扑线性空间并研究了它们的一些性质.目前,改进集已成为研究向量优化问题近似解,特别是统一形式的近似解的重要工具之一[12-14].特别地,文献[12]基于改进集提出了邻近E-次似凸性概念和集值向量优化问题弱E-最优解概念,并建立了邻近E-次似凸性假设条件下的择一性定理和近似解的线性标量化定理等.文献[13]基于改进集提出了E-Benson真有效解的概念,并基于E-次似凸性下的择一性定理建立了这类近似真有效解的线性标量化定理和拉格朗日乘子定理等.
受文献[8-9,12-13]中相关研究工作的启发,本文利用改进集和非线性标量化函数等工具建立了集值映射的Ekeland变分原理.本文所建立的新的集值Ekeland变分原理包含了一些经典形式的Ekeland变分原理作为其特例.
2 预备知识
假定(X,d)是度量空间,Y是局部凸空间,Rn表示n维欧几里得空间,Rn+表示Rn中的非负象限锥,N+表示正整数全体.设A⊆Y,int A、∂A和YA分别表示A的拓扑内部、A的边界和A的补集.A的锥包为:
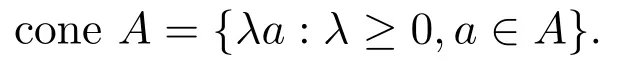
锥K⊆Y称为点的,若K∩(-K)={0}.设K为Y中具有非空拓扑内部的闭凸点锥,Y中由K诱导的偏序定义为对任意的x,y∈Y,x≤Ky⇔y-x∈K.
设F:X⇒Y为集值映射.称F为K-闭的,若对任意的x∈X,F(x)+K是闭的.称F(X)是K-有界的,若存在有界集M⊆Y使得F(X)⊆M+K.
定义2.1[8]称(X,d)为(F,K)-下完备的,若Cauchy点列{xn}⊆X收敛且满足对任意的正整数n,F(xn)⊆F(xn+1)+K.
定义2.2[8]称F为K-序列下单调的,若对任意的正整数n,F(xn)⊆F(xn+1)+K且蕴含
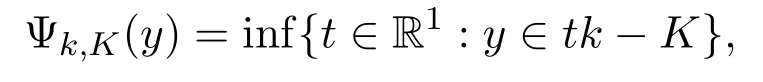
其中k∈Y,∅≠K⊆Y,inf∅=+∞.
引理2.1[8]设k∈int K,则Ψk,K是次线性下半连续函数且具有如下性质:
(i)Ψk,K(y)<r⇔y∈rk-int K;
(ii)Ψk,K(y)≤r⇔y∈rk-K;
(iii)Ψk,K(y)=r⇔y∈rk-∂K;特别地,Ψk,K(k)=1,Ψk,K(λk)=λ,∀λ∈R1;
(iv)Ψk,K(y)≥r⇔y∉rk-int K;
(v)Ψk,K(y)>r⇔y∉rk-K;
(vi)Ψk,K(y+λk)=Ψk,K(y)+λ,∀y∈Y,∀λ∈R1;
(vii)y1≤Ky2⇒Ψk,K(y1)≤Ψk,K(y2).
定义2.3[1012]称非空集E⊆Y为关于K的改进集,若0∉E且E+K=E.Y中关于K的全体改进集簇记为
注2.1由文献[12]中的引理2.1可知,int K≠∅蕴含int E≠∅.
3 基于改进集的集值Ekeland变分原理
本节主要利用非线性标量化函数及其相应的非凸分离定理建立基于改建集的集值Ekeland变分原理,并讨论它的一些特殊情形.
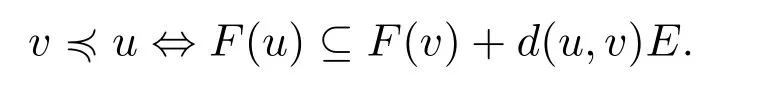
则≼满足自反性和传递性.




注3.1令k0∈int K,ε>0且E=εk0+K.则定理3.1可退化为文献[8]中定理3.1的λ=1的情况.
注3.2令k∈int K,ε>0,δ>0且E=(ε+δ)k+K.则定理3.1退化为文献[6]中定理5.2的λ=1的情况.
若F为单值的,则下面的推论3.1是定理3.1的直接结果.

[1]Ekeland I.On the variational principle[J].Journal of Mathematical Analysis and Applications,1974,47(2):324-353.
[2]Ekeland I.Nonconvex minimization problems[J].Bulletin(New Series)of the American Mathematical Society,1979,1(3):443-474.
[3]Chen Guangya,Huang Xuexiang,Hou S H.General Ekeland′s variational principle for set-valued mappings[J].Journal of Optimization Theory and Applications,2000,106(1):151-164.
[4]Ha T X D.Some variants of the Ekeland variational principle for a set-valued map[J].Journal of Optimization Theory and Applications,2005,124(1):187-206.
[5]Guti´errez C,Jim´enez B,Novo V.A set-valued Ekeland′s variational principle in vector optimization[J].SIAM Journal on Control and Optimization,2008,47(2):883-903.
[6]Guti´errez C,Jim´enez B,Novo V,et al.Strict approximate solutions in set-valued optimization with applications to the approximate Ekeland variational principle[J].Nonlinear Analysis,2010,73(12):3842-3855.
[7]Khanh P Q,Quy D N.On generalized Ekeland′s variational principle and equivalent formulations for set-valued mappings[J].Journal of Global Optimization,2011,49(3):381-396.
[8]Qiu Jinghui.On Ha′s version of set-valued Ekeland′s variational principle[J].Acta Mathematica Sinica,English Series,2012,28(4):717-726.
[9]Qiu Jinghui.Set-valued quasi-metrics and a general Ekeland′s variational principle in vector optimization[J].SIAM Journal on Control and Optimization,2013,51(2):1350-1371.
[10]Chicco M,Mignanego F,Pusillo L,et al.Vector optimization problem via improvement sets[J].Journal of Optimization Theory and Applications,2011,150(3):516-529.
[11]Guti´errez C,Jim´enez B,Novo V.Improvement sets and vector optimization[J].European Journal of Operational Research,2012,223(2):304-311.
[12]Zhao Kequan,Yang Xinmin,Peng Jianwen.Weak E-optimal solution in vector optimization[J].Taiwanese Journal of Mathematics,2013,17(4):1287-1302.
[13]Zhao Kequan,Yang Xinmin.E-Benson proper efficiency in vector optimization[J].Optimization,2015,64(4):739-752.
[14]Zhao Kequan,Yang Xinmin.A unified stability result with perturbations in vector optimization[J].Optimization Letters,2013,7(8):1913-1919.
Ekeland′s variational principle via improvement sets for set-valued maps
Wan Xuan1,Zhang Wanli2,Zhao Kequan2
(1.Department of Foundation,Chongqing Telecommunication Polytechnic College,Chongqing402247,China;2.College of Mathematics Science,Chongqing Normal University,Chongqing401331,China)
Ekeland′s variational principles have been playing a very important role in optimization theory and it′s applications.In this paper,based on improvement sets,we establish an Ekeland′s variational principle for set-valued maps by using a kind of nonlinear scalarization function and its corresponding nonconvex separation theorem.New Ekeland′s variational principle includes some classical Ekeland′s variational principles as its special cases.
improvement sets,Ekeland′s variational principle,set-valued maps,nonlinear scalarizaion function
O176;O177.9
A
1008-5513(2015)06-0567-08
10.3969/j.issn.1008-5513.2015.06.003
2015-05-15.
国家自然科学基金(11301574,11271391);重庆市基础与前沿研究计划项目(cstc2015jcyjA00027);重庆市教委科学技术研究项目(KJ1500303);第二批重庆市高等学校青年骨干教师资助计划.
万轩(1987-),硕士,讲师,研究方向:向量优化理论与方法.
2010 MSC:65K10

