阻尼耦合轮对动力学性能及最佳耦合度研究

王　军平，黄运华，丁军　君，

（1 中铁物总技术有限公司，北京100032；2 西南交通大学 机械工程学院，四川成都610031）

阻尼耦合轮对动力学性能及最佳耦合度研究

王军平1，黄运华2，丁军君1，2

（1 中铁物总技术有限公司，北京100032；2 西南交通大学 机械工程学院，四川成都610031）

阻尼耦合轮对是一种较新型的轮轨导向系统，现建立阻尼耦合轮对车辆的动力学模型，系统地分析了耦合阻尼对其直线稳定性和曲线上轮轨横向力的影响，并得出了轮对最佳耦合阻尼取值范围。研究发现，选择适当的耦合度时，阻尼耦合轮对的应用能够克服转向架临界速度的提高和曲线通过性能的提升之间的矛盾，使二者同时得到改善。

阻尼耦合轮对；临界速度；轮轨横向力；轮对耦合方式

车辆蛇行临界速度的提高和曲线通过性能的改善对转向架悬挂参数的要求是恰好相反的，车辆运行速度的提高势必会使其曲线通过性能下降。在当今铁道车辆轮轨导向系统中，多以传统轮对为主，传统轮对具有较好的曲线通过性能，但蛇行临界速度受限；采用独立旋转车轮的转向架虽然临界速度得到大幅提升，同时能够通过小半径曲线，但轮缘磨耗非常严重，工程实用难度较大。因此很有必要研究一种既能提高转向架蛇行临界速度也能改善其曲线通过性能的新型轮对，耦合轮对就是满足这种要求的轮对形式之一。耦合轮对是指轮对的左右车轮既不完全固结在一起，也不完全独立，而是通过耦合器达到适当程度的联系，从而发挥传统轮对和独立旋转车轮的优点，同时克服二者的不足，达到较理想的动力学性能要求［1］，耦合轮对耦合器的形式有弹性阻尼、离心、气动、电磁、液压等多种形式［2］。阻尼耦合轮对是其中的一种，其左右轮对通过阻尼耦合器相连，当左右车轮存在旋转角差时便存在扭转力矩，通过对耦合阻尼的调整得到理想的耦合力矩，从而得到理想的纵向蠕滑力，进而使耦合轮对获得理想的动力学性能。

借助Sim pack动力学仿真分析软件系统地对阻尼耦合轮对（Dam per Coupled W heelset，文中用DCW表示）进行研究，分析耦合阻尼对其直线稳定性和曲线上轮轨横向力的影响，并对前后轮对选用相同耦合度和不同耦合度两种形式转向架的性能进行研究，得出两种结构形式下轮对最佳耦合阻尼取值范围，为阻尼耦合轮对在实际中的应用提供一定的参考。

1　动力学计算模型及线路设置

图1所示为整体转向架结构的DCW 车辆系统动力学计算模型，模型中忽略了车辆间的相互影响，车辆的各个刚体之间是通过弹簧和减振器连接的，其中各刚体自由度的选择如表1所示。

图1　车辆动力学计算模型

表1　阻尼耦合轮对车辆系统各刚体自由度设置

表1中，k=1、2，分别代表前、后转向架构架；i=1～4分别代表1～4位轮对。由于DCW左右车轮的点头角速度不一定相同，所以分别用φw Li和φw Ri表示。整个车辆的自由度为31个。

分析所采用的轨道为60 kg/m钢轨，车轮踏面为L M磨耗型踏面，轮轨摩擦系数为0.3。分析中，在曲线段上采用的激扰为超高和曲率，不考虑轨道不平顺。曲线线路是由一段超高和曲率都固定的圆曲线及其两端各有一段超高和曲率都不断变化的缓和曲线组成。具体线路设置为直线（30 m）→缓和曲线（100 m）→圆曲线（100 m）→缓和曲线（100 m）→直线，外轨最大超高100 m m，设定最大欠超高60 m m，通过曲线时的速度按照文献［3］第一章中的方法确定，取允许值的最大值。

2　运动方程

在DCW中，左右车轮是通过耦合器连接的，当左右车轮有不同的旋转角时，可以得到不同的耦合力矩。假设左右车轮的旋转角分别为φw L和φw R，则相应的旋转角速度分别为φ·w L和φ·ω R，此时，耦合力矩为：

式中C为耦合阻尼系数，通过调节耦合阻尼值，可以得到不同的耦合度，对应不同的动力学性能。

DCW车辆的构架和车体的受力情况与传统车辆相似，其运动方程也类似，这里不再赘述，仅将DCW的运动方程罗列如下：

轮对横移：

轮对摇头：

轮对点头：

方程中φwsi=（φw Li+φw Ri）/2，φwdi=（φw Li-φw Ri）/2，式（2）～式（5）中i=1～4；Mw为轮对质量，kg；r0为轮对标称滚动圆半径，m；φsewi为线路实 际超高角，rad；Kgyi为重力角刚度，k N/m；v为车辆前进速度，km/h；Rwi为实际曲线半径，m；TLyi、TRyi为左右车轮横向蠕滑力，k N；TLxi、TRxi为左右车轮纵向蠕滑力，k N；TLzi、TRzi为左右车轮垂向蠕滑力k N；NLyi、NRyi为左右车轮法向力的横向分力，k N；NLzi、NRzi为左右车轮法向力 的垂向 分力，k N；Fpwyi为一系悬挂横向力，k N；Iwy、；Iwz分别为轮对绕y、z轴的惯性矩，kg·m2；φwi为轮对侧滚角，rad；a为左右轮轨接触点的横向间距之半，m；rLi、rRi为左右车轮的滚动圆半径，m；Mpwzi为一系悬挂摇头力矩，k N ·m；MLyi、MRyi为左右车轮自旋蠕滑力矩在y轴的分量，k N·m；MLzi、MRzi为左右车轮自旋蠕滑力矩在z轴的分量，k N·m；Ci为耦合阻尼，N·m·s/rad。

3　转向架前后轮对耦合度相同时的性能

3.1耦合阻尼对临界速度的影响

当转向架前后轮对选用相同耦合度的DCW时，耦合阻尼值对车辆系统临界速度的影响如图2所示。由图可知，在小耦合阻尼（0～100 N·m·s/rad）时，临界速度为很高的值，随着耦合阻尼的增加，临界速度呈下降趋势，当耦合阻尼在5×102～5×105N·m·s/rad范围内变化时，临界速度随耦合度的变化较为明显，当耦合阻尼值超过5×105N·m·s/rad时，临界速度基本保持恒定（290 km/h），不再随耦合阻尼的变化而变化。对相同参数，相同条件下的传统轮对进行计算分析可知，其临界速度也为290 km/h，说明当耦合阻尼取值足够大时，阻尼耦合轮对性能与传统轮对相当。

图2　耦合阻尼对DCW临界速度的影响

3.2耦合阻尼对曲线上轮轨横向力的影响

图3列举了通过不同半径曲线时，耦合阻尼对DCW轮轨横向力的影响，图中各值为通过曲线时轮轨横向力的绝对最大值，图中，IR W表示独立旋转车轮，T R A表示传统轮对。

由图3可知，在曲线段上，导向轮对的轮轨横向力随耦合阻尼和曲线半径的增大而下降，而跟随轮对轮轨横向力的变化趋势相反，随耦合阻尼的增大而增大，同时，对比图3（a）、（b）图发现，在小耦合度时，跟随轮对轮轨横向力恒小于导向轮，而在大耦合度下，曲线半径较大时，跟随轮对轮轨横向力大于导向轮。分析可知，从轮轨横向力分析，增加导向轮对的耦合度有利于减小轮轨最大横向作用力，即可以改善转向架的曲线通过性能，而跟随轮对耦合度的增加会恶化转向架的曲线通过性能。文中在对能体现转向架曲线通过性能的轮对冲角、纵向蠕滑力和轮缘力等指标的计算中发现，各指标所体现出的趋势与轮轨横向力体现出的趋势相类似，为减少文章篇幅，本节及以下章节均以轮轨横向力作为主要指标研究转向架的曲线通过性能，对其他各指标的趋势不再赘述。

同时可发现，轮轨横向力对耦合阻尼的敏感区间为5×102～5×105N·m·s/rad，当耦合阻尼趋近于0和∞时DCW的性能能够很好地与独立旋转车轮和传统轮对相吻合。

图3　曲线上耦合阻尼对轮轨横向力的影响

3.3最佳耦合度选择

由3.2节分析可知，整体而言，耦合阻尼的增加对转向架性能来说是有利的，但由于导向轮对和跟随轮对轮轨横向力的变化趋势不同，因此需要对其进行进一步研究，才能确定合适的耦合阻尼取值。

图4为车辆系统通过半径为700 m曲线段时的轮轨横向力随耦合阻尼的变化情况，由图4可知，随着耦合阻尼的增加，导向轮对轮轨横向力逐渐下降，跟随轮对轮轨横向力逐渐增加，在耦合阻尼为1×104N·m·s/rad左右处出现交叉，此时的轮轨横向力出现最小值，该值小于传统轮对通过相同曲线时的轮轨横向力（图中T R A虚线对应值）。对不同半径曲线上轮轨横向力进行分析可得类似结果，可见，选取适当耦合阻尼值时，DCW的应用能够减小轮轨横向作用力，从而改善转向架的曲线通过性能。

图4　轮轨横向力随耦合阻尼的变化（R=700）

表2所示为不同耦合阻尼下转向架临界速度与传统轮对（T R A）的比值γ及不同曲线半径下轮轨横向力的最大值与传统轮对的比值，表中，耦合阻尼的单位为牛顿·米·秒·每弧度，曲线半径单位为米。由表可知，当曲线半径R=300 m时，轮轨横向力的最小值出现在耦合阻尼C=5×105N·m·s/rad左右，最小轮轨横向力较传统轮对下降了0.1%，此耦合阻尼时在直线线路上转向架临界速度较传统轮对提升了0.3%；R= 500 m时，轮轨横向力最小值出现在C=5×104N·m· s/rad左右，与传统轮对相比，轮轨横向力减小了10. 7%，临界速度提高了2.1%；R=700 m时，轮轨横向力最小值出现在C=1×104N·m·s/rad，轮轨横向力减小了28.8%，临界速度提高了6.9%；R=900 m时，轮轨横向力最小值出现在C=5×103N·m·s/rad左右，轮轨横向力减小了32.1%，临界速度提高了11%。

表2　耦合阻尼对DCW临界速度和轮轨横向力的影响

结合图4和表2可知，当DCW选用合适的耦合阻尼时，能够克服转向架临界速度的提高和曲线通过性能的改善之间的矛盾，使二者同时得到提高。当导向轮对和跟随轮对轮轨横向力相等时，转向架通过曲线时对线路的作用力最小，对应阻尼值即为最优耦合阻尼，对不同曲线半径下的最优耦合阻尼进行详细计算分析所得结果见表3。

表3　曲线上最佳耦合阻尼取值范围

由表3可知，随着曲线半径的增大，最佳耦合阻尼值逐渐减小。

4　转向架前后轮对耦合度不同时的性能

对转向架前后轮对选用不同耦合阻尼时的转向架动力学性能进行分析，以获得轮对最佳耦合方式。由第3节内容可知，当DCW耦合阻尼取值趋近于0时，其动力学性能与独立旋转车轮相似，当耦合阻尼取值为∞时，其性能与传统轮对相当。因此，首先选择转向架前后轮对的耦合阻尼分别为0，5×104N·m·s/rad（耦合阻尼敏感区间内的值）和∞这几种特殊情况，对其性能进行分析，观察转向架前后轮对耦合度对性能的影响。

4.1轮对耦合方式对临界速度的影响

图5为转向架临界速度随轮对耦合方式的变化曲线，图中横坐标为轮对耦合方式，“+”前为导向轮对类型，“+”后为跟随轮对类型，T表示传统轮对，D表示DCW，I表示独立旋转车轮。

图5　轮对耦合方式对　DCW临界速度的影响

由图5可知，临界速度随跟随轮对类型从传统轮对→DCW→独立旋转车轮依次递增，跟随轮对为传统轮对和DCW时的临界速度远小于独立旋转车轮时的值，其中，独立旋转车轮转向架（I+I）在理论上临界速度为无穷大，这里为了作图方便，用400 km/h代表其临界速度，在此速度时，独立旋转车轮转向架运行情况良好。同时，临界速度随导向轮对类型从传统轮→E DCW→独立轮依次增大，随导向轮对类型的变化趋势与跟随轮对相比较为平缓。变化导向轮对和跟随轮对的耦合度对临界速度的影响效果类似，但变化跟随轮对耦合度时的效果更为显著。

4.2轮对耦合方式对曲线上轮轨横向力的影响

图6为DCW轮轨横向力随轮对耦合方式的变化曲线图，图6中各值为转向架通过曲线时轮轨横向力的绝对最大值。由图6（a）可知，导向轮对轮轨横向力随曲线半径的增大而减小，轮轨横向力随导向轮对类型从传统轮对→耦合轮对→独立旋转车轮递增。小半径曲线时，跟随轮对为独立旋转车轮时的轮轨横向力最小，曲线半径较大时，当导向轮对为传统轮对和耦合轮对时的轮轨横向力相差不大。由图6（b）可知，跟随轮对轮轨横向力随导向/跟随轮对类型从传统轮对→耦合轮对→独立旋转车轮依次递增/减。

图6　轮对耦合方式对DCW曲线上轮轨横向力的影响

综合4.1节内容可知，当导向轮对选取为传统轮对或耦合轮对，跟随轮对为独立旋转车轮时转向架临界速度最高，且导向/跟随轮对轮轨横向力较小。也就是说当跟随轮对耦合度为0，导向轮对耦合度较大时转向架性能较好。

4.3最佳耦合度选择

按照3.3节同样方法对跟随轮对耦合阻尼为0，导向轮对选取不同耦合阻尼时的转向架性能进行分析来获得这种轮对耦合方式下的最佳耦合度取值范围。

表4为当跟随轮对耦合度为0时，导向轮对选取不同耦合阻尼时转向架临界速度与传统轮对的比值γ及不同曲线半径下轮轨横向力与传统轮对的比值，阻尼。

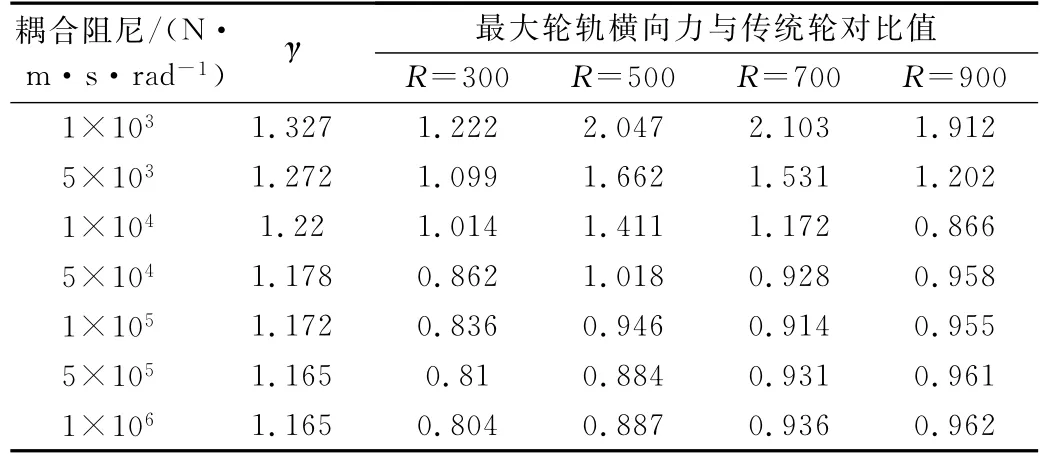
表4　导向轮对耦合阻尼对临界速度和轮轨横向力的影响

由表4可知，当曲线半径R=300 m时，轮轨横向力的最小值出现在导向轮对耦合阻尼为1×106N·m ·s/rad左右，轮轨横向力较传统轮对下降了19.6%，此耦合阻尼时在直线线路上转向架临界速度较传统轮对提升了16.5%；R=500 m时，轮轨横向力最小值出现在C=5×105N·m·s/rad左右，与传统轮对相比减小了11.3%，临界速度提高了16.5%；R=700 m时，轮轨横向力最小值出现在C=1×105N·m·s/rad左右，轮轨横向力减小了8.6%，临界速度提高了17.2%；R= 900 m时，轮轨横向力最小值出现在C=1×104N·m ·s/rad左右，轮轨横向力减小了13.4%，临界速度提高了22%。对不同曲线半径下的最优耦合阻尼进行详细计算分析所得结果见表5。

将表5的结果和表3进行对比可发现，当跟随轮对耦合阻尼取值为0时，导向轮对选取合适的耦合阻尼时同样可以同时提高转向架临界速度和曲线通过性。相比之下，当前后轮对选用相同耦合参数时，耦合度的选择对曲线上轮轨横向力的减小效果较明显，而当跟随轮对耦合阻尼为0时，导向轮对耦合度的选择对直线上临界速度的提高效果较好。

表5　曲线上导向轮对最佳耦合阻尼取值范围

5　结 论

研究了耦合阻尼值对前后轮对选用相同耦合度和不同耦合度时的转向架临界速度和轮轨横向力的影响，得到了两种结构形式下轮对最佳耦合阻尼取值范围，通过分析可以得出以下结论：

（1）当耦合阻尼趋近于0时，DCW性能与独立旋转车轮相当，当耦合阻尼趋近于∞时，其性能与传统轮对相吻合。

（2）DCW对耦合阻尼的敏感区间为5×102～5× 105N·m·s/rad，当阻尼值在该范围内变化时，性能变化较明显，超出该范围时，对动力学性能的影响较小。

（3）选取耦合阻尼值时，阻尼耦合轮对的应用能够克服转向架临界速度的提高和曲线通过性能的提升之间的矛盾，使二者同时得到改善。

（4）转向架前后轮对选用相同耦合阻尼的DCW时，耦合阻尼值的选择对系统曲线通过性能的改善效果较好，而当跟随轮对耦合阻尼为0时，导向轮对耦合阻尼的选择对转向架临界速度的提高效果较明显。

（5）耦合阻尼的合理取值区间为5～1 000 k N·m ·s/rad，理想耦合阻尼值随曲线半径的变化较大，因此，很有必要研究耦合阻尼的主动控制技术，使得耦合阻尼可以随车辆运行速度和曲线半径的变化而发生变化，从而能够更好地利用DCW的优势。

［1］ 王开文，池茂儒.耦合轮对的发展［J］.铁道车辆，2002，40（12）：1-3.

［2］ A h med A KW，Sankar S.Lateral Stability Behavior of Railway Freight Car System with Elasto-Dam per Coupled W heelset：part2-TruckM odel［J］.Journal ofM echanisms，Transmissions，and A uto mation in Design，1987. 109（12）：500-507.

［3］ 严隽耄，傅茂海.车辆工程［M］.第3版.北京：中国铁道出版社，2008.

［4］ A H ME D A K W，S A N K A RS.Steady-state curving performance of railway freight truckwith dam per coupled w heelsets［J］.Vehicle SystemDynamics.1998，17：295-315.

［5］ R.V.D U K KI，S.N A R A Y A N A S W A M Y，M.O.M.O SM A N.Independently rotating w heel systems for railway vehicles-A stat e of the art review［J］.Vehicle System Dynamics.1992，21：297-330.

［6］ 李 芾，黄运华，傅茂海.车轮耦合方式发展及其导向机理［J］.机车电传动.2006，（2）：1-4，9.

A Study of Dynamic Performance and the Best Coupling Factor of Dam per Coupled W heelset

W A N G Junping1，H U A N G Yunhua2，DI N G Junjun1，2
（1 China Railway M aterials Technologies Co m pany Limited，Beijing 100032，China；2 School of M echanical Engineering of South west Jiaotong U niversity，Chengdu 610031 Sichuan，China）

Dam per coupled w heelsetis a relatively new type of w heel-rail guiding system.In this paper，the dynamic calculating m odel of a vehicle with dam per coupled w heelsetis established，the influence of coupling dam per on its straightline stability and w heel-raillateral force is systematically analyzed，and the best range of coupling factor is calculated as well.It is found that w hen choosing reasonable coupling factor，the contradiction between critical speed im provement and curving performance enhancement of one bogie can be overco me and both im proved due to the applications of dam per coupled w heelset.

dam per coupled w heelset；critical speed；w heel-raillateral force；coupling m ode of w heelset

U260.11+1

A

10.3969/j.issn.1008-7842.2015.05.08

1008-7842（2015）05-0038-05

王军平（1988—）男，工程师（2015-03-17）