超声造影剂微泡非线性声学特性的数值仿真

许小芳，周红生，杨红穗，刘春泽



超声造影剂微泡非线性声学特性的数值仿真

许小芳，周红生，杨红穗，刘春泽

(中国科学院声学研究所东海研究站，上海200032)

以空气泡为例，采用描述气泡半径运动的Rayleigh-Plesset方程，对其在高频声压辐照下的非线性振荡，散射声场和散射截面进行理论和数值研究，为获取更清晰的图像提供理论依据。结果表明：激励声压的频率在微泡的固有谐振频率附近时，可以产生强的二次谐波散射声压。同时，提高入射声强可以增大二次谐波散射截面, 但不能改变基波散射截面。

超声造影剂；非线性声学特性；基波；二次谐波

0 引言

超声造影剂的发展和应用，大大促进了医学超声的进展，使得医学超声进入了人体微循环系统的诊断和治疗的新阶段[1-2]。一方面，由于造影剂的声阻抗特性与生物组织存在很大差异，因此，入射到微泡上的超声波将发生强烈散射，极大地增强了回波信号，提高了检测的信噪比。对于直径小于10 μm的造影剂，它可以进入各脏器中的毛细血管，这样，处于肌肉深处的病灶和微循环系统可获得高反差的声像。另一方面，造影剂在超声激励下可产生非线性振动，激发高次谐波，利用谐波成像，可大大提高成像的空间分辨率。

目前，超声造影剂已从第一代游离气泡发展成为以白蛋白、磷脂、半乳糖、聚合物、液膜(表面活化剂)等材料为外壳并包裹着高分子量难溶气体成分的第四代造影剂，其优点在于延长了微泡的寿命，使得微泡内的气体不容易溶解，提高了微泡的稳定性，但是同时也影响了微泡在声场中的振动，使其在声场中的振荡特性变得更复杂。

研究表明[3]，超声造影剂在医学诊断和治疗上的应用，与微泡在声场中的非线性散射特性紧密相关。因此，为了更好地了解超声造影剂在声场作用下的振动行为，获取更清晰的物理图像，本文以空气微泡为例，采用单个微泡在声场中振动的理论模型，对其在声场中的非线性振荡，散射声场和散射截面进行理论和数值研究。

1 非线性振荡

当液体中的气泡保持平衡时，泡内和泡外的压力满足静力平衡条件[5]：

当气泡受入射声波激励时，除了弹性散射外[6]，还将作受迫的非线性振动，因而它会产生基频及高次谐频的散射声波。

在Matlab中采用四阶龙格-库塔法对式(3)进行求解，得到气泡的曲线如图1所示，所选用的参数如表1所示。

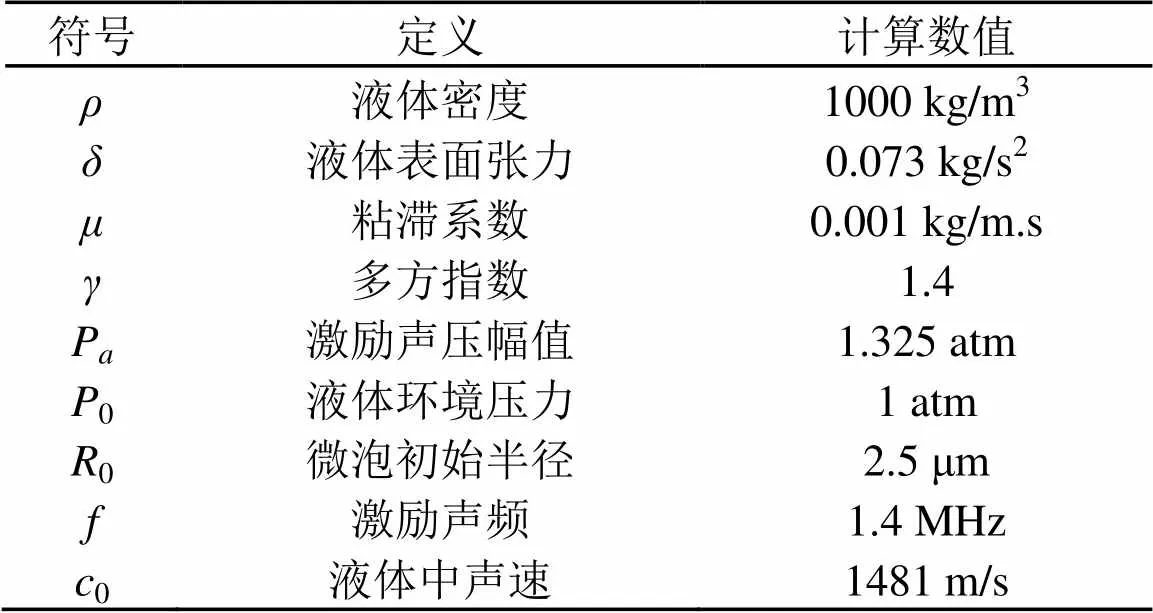
表1 计算参数符号定义及取值

对气泡的()作傅里叶变换，可以得到()的基频和高次谐频分量的频谱，如图2所示。从图2中可以看出，气泡的非线性运动可以产生除基波外的多阶高次谐波振动。

图2 R(t)频谱

为了得到进一步的清晰图像，假设气泡半径在声压的作用下发生微小的变化[8-9]：

联立式(1)~式(3)，可得：

(5)

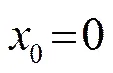
(7)

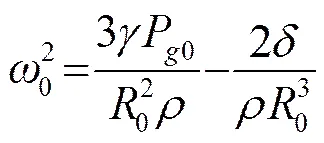
因此，微泡的半径()可表示为：

(9)

图3 x1和x2与f的关系

2 非线性散射声场

声场中振动的微泡将向液体中辐射声波。在球坐标系统中，液体中球对称振动的微泡在处产生的辐射声场满足波动方程[6]：

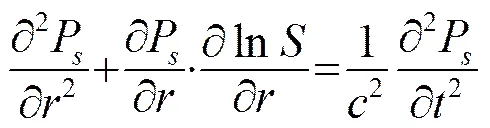
其中：是液体的声速；为波阵面的面积函数，且球坐标下=4π2。因此，式(10)可写成：

(11)

满足波动方程式(11)的基波和二次谐波的散射声压可分别表示为：

由运动方程

(13)

可得到散射声场中质点的振动速度为

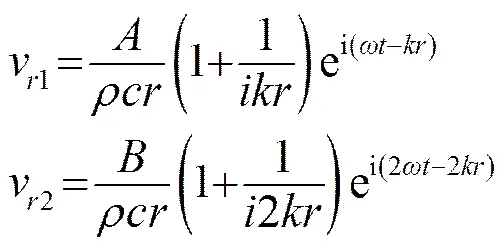
(15)

由式(9)，得到气泡壁面的振动速度为

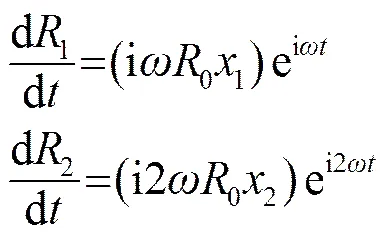
所以，v1和v2中的常数和可以由边界条件式(15)确定：

，(17)

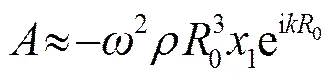
(18)

因此，将式(18)代入式(12)可得到微泡非线性振荡而形成的散射声场：

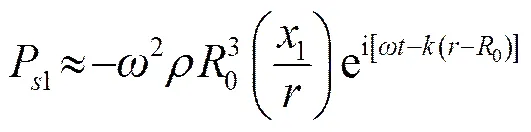
(19)

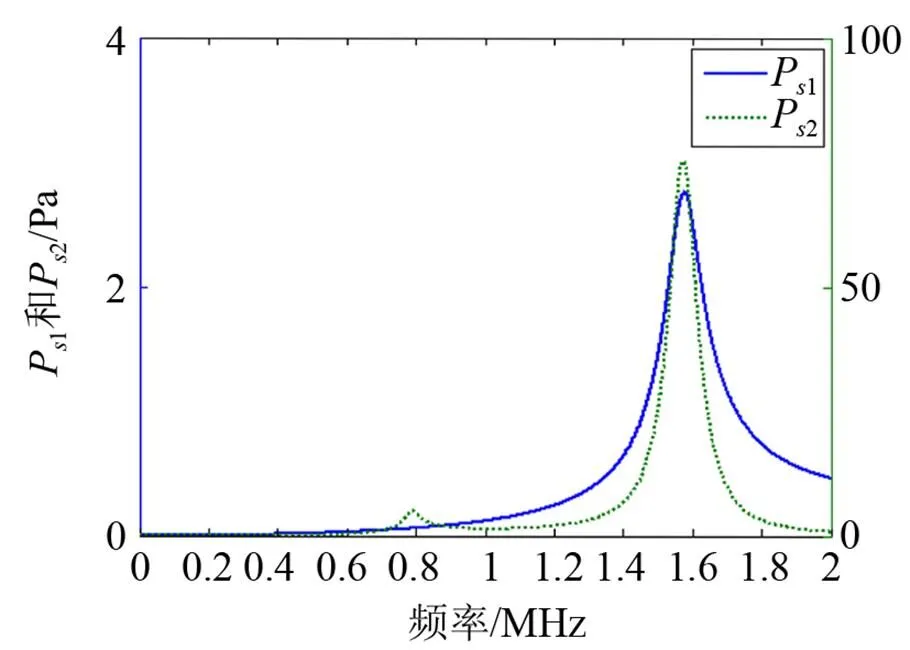
图4 Ps1和Ps2与f的关系

3 散射截面

各向同性散射体的声散射截面可表示为[10]：

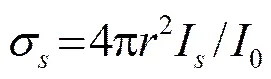
在远场条件下：

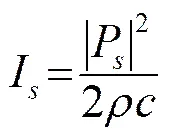
于是，式(21)可表示为：

(22)

将式(19)代入式(22)，得到微泡的基波和二次谐波的声散射截面和：

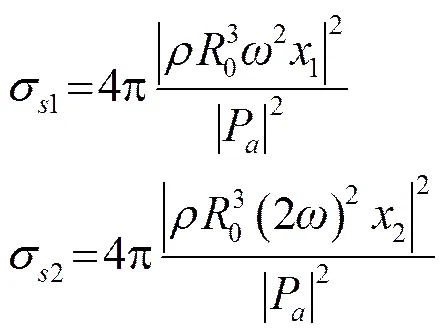
(a)P=105Pa

(b)P=2Í105Pa

图51和2与的关系

Fig.5 The curves ofvs.σ1andσ2

4 结论

在绝热条件下，利用RPNNP方程，对微泡运动的非线性声学特性进行数值求解，得到了液体中微泡非线性振荡而形成的基波及二次谐波散射声场及散射截面。结果表明：当激励声场的频率在微泡的固有谐振频率附近时，能产生较强的基波和二次谐波的声散射。提高入射声波声压，可以增大二次谐波的散射截面。但不能增加基波的散射截面。因此，谐波成像时，超声波的工作频率宜与微泡谐振频率相近，以利于提高信噪比。

[1] Blomley M J K, Cooke J C, Unger E C, et al. Microbubble contrast agents: a new era in ultrasound[J]. Science, medicine, and the future, 2001, 322(7296): 1222-1225.

[2] Harvery C J, Plicher J M. Advences in ultrasound[J]. Clinical Radiology, 2002, 57(3): 157-177.

[3] 钱梦騄. 超声造影剂及其应用[J]. 声学技术, 2004, 23(3): 1-2.

QIAN Menglu. Ultrasound contrast agent and its applications[J]. Technical Acoustics, 2004, 23(3): 1-2.

[4] 王捷. 基于Matlab的超声空化气泡动态仿真[J]. 西安邮电学院学报, 2012, 17(S1): 6-8.

WANG Jie. Simulation of ultrasonic cavitation bubble dynamics based on Matlab[J]. Journal of Xi’an University of Posts and TelEcommunications, 2012, 17(S1): 6-8.

[5] 钱梦騄. 单泡声致发光中气泡的动力学特性-振子模型[J]. 声学学报. 2002, 27(4): 290-294.

QIAN Menglu. Dynamic behavior of gas bubble in single sonoluminescence-vibrator model[J]. Acta Acustica, 2002, 27(4): 290-294.

[6] 杜功焕. 声学基础[M]. 南京: 南京大学出版社, 2001.

DU Gonghuan. Fundamentals of acoustics[M]. Nanjing: Nanjing University Press, 2001.

[7] 钱梦騄, 程茜. 单泡声致发光—气泡的动力学特性[J]. 声学技术, 2003, 22(3): 203-206.

Qian Menglu. Cheng Qian.Single bubble sonoluminescence- Dynamic behavior of gas bubbles[J]. Technical Acoustics, 2003, 22(3): 203-206.

[8] WU Chungyou. The ultrasonic weak short-pulse responses of microbubbles based on a two-frequency approximation[J].J. Acoust. Soc. Am., 2003, 114 (5): 2262-2264.

[9] LI Fei, FAN Yubo. The acoustic nonlinearity of a single ultrasound contrast agent microbulle[C]// International Conference on Bioinformatics & Biomedical Engineering, 2011: 1-4.

[10] Church C C. The effect of an elastic solid surface layer on the radial radiations of gas bubbles[J]. J. Acoust. Soc. Am, 1995, 97(3): 1510-1521.

Numerical simulation on the nonlinear acoustic characteristics of ultrasonic contrast-agent

XU Xiao-fang, ZHOU Hong-sheng, YANG Hong-sui, LIU Chun-ze

(Shanghai Acoustics Laboratory, Chinese Academy of Science, Shanghai 200032, China)

Aimed to provide theoretical basis for acquiring more distinct images, some theoretical and numerical research on nonlinear vibration,scattering acoustic field and scattering cross section of bubbles under high frequency acoustic radiation have been done based on the Rayleigh-Plesset equation describing bubbles'radius movement. The simulations show that strong secondary harmonic scattering acoustic pressure can be obtained when the frequency of driven acoustic pressure is near bubbles' inherent frequency, while higher incident acoustic pressure can increase secondary harmonic scattering cross section rather than fundamental wave scattering cross section.

ultrasonic contrast agent; nonlinear acoustic properties; fundamental; second harmonics.

O426.1

A

1000-3630(2015)-06-0521-04

10.16300/j.cnki.1000-3630.2015.06.010

2015-08-11;

2015-11-14

国家自然科学基金项目(11274342、11304353、11474042、11574348)。

许小芳(1984－), 女, 安徽池州人, 硕士, 助理研究员, 研究方向为超声应用。

周红生, E-mail: zhs999@126.com