哈特曼发声器阵列的声学特性研究

陈仁松，王国庆，陈修海，高新军，贾俊波，裴永泉



哈特曼发声器阵列的声学特性研究

陈仁松，王国庆，陈修海，高新军，贾俊波，裴永泉

(陕西省宝鸡市150信箱11分箱28号，陕西宝鸡721013)

论文采用FW-H声模拟法，对入口气压分别为3.12、4.12、5.12、6.12、7.12和8.12 atm的哈特曼发声器阵列的声场声学性能进行了数值计算。对声场声强进行了非线性回归分析，得出了声场的声强经验公式。并对回归进行方差分析和F分布检验，分析结果显示，置信水平可以达到10-4，回归水平显著，经验公式的可信度很高。论文结论对哈特曼发声器阵列的应用具有重要的指导意义。

哈特曼超声波发生器阵列；FW-H声模拟法；声学特性

0 引言

流体哈特曼超声波发声器是由丹麦学者Hartmann[1-2]在1918年提出的一种流体动力型声波发声器，1954年Sprenger H[3]发现了谐振腔底部存在的热效应并用于发动机的点火装置后，又称为Hartmann-Sprenger tube。哈特曼发声器结构简单、体积小、耐冲击，可以在恶劣的条件下工作。只要材料强度条件允许，就可以在较高的压强下产生大功率的声辐射。同时，哈特曼发声器还具有造价低廉、处理量大、操作方便、经久耐用等特点，被广泛应用在如声波除灰、解堵、防垢、防蜡、降粘、加速化学反应、抑制飞机冲击噪声、空穴噪声等多方面。

为了提高哈特发声器的发声效率，可通过多个哈特曼发声器组成哈特曼阵来增大发射功率。但这方面的研究文献资料国内外非常少。在国内，谷嘉锦[4]用一组四个带中心棒、不同规格的哈特曼发声器进行了简单的实验测试。为满足高功率超声设计需要，提出了单层和多层哈特曼超声波发声器阵列的设计思路，并对其流体力学和声学特性进行了初步的仿真计算[5-7]。

本文利用FW-H声模拟法，对哈特曼发声器阵列的声学特性进行了研究。具体研究单层、两层和三层哈特曼发声器阵列的不同入口气压条件下的声场声强，对计算结果进行了非线性回归分析，得出了哈特曼发声器阵列声场声强的经验公式。论文结论对哈特曼发声器阵列的应用具有重要的指导意义。

1 数值计算方法

1.1 声模拟法

声模拟法基于Ffowcs Williams-Hawkings (FW- H)方程的，而FW-H方程是从连续性方程和Navier- Stokes方程推导得到的，FW-H方程如下式[6-7]：

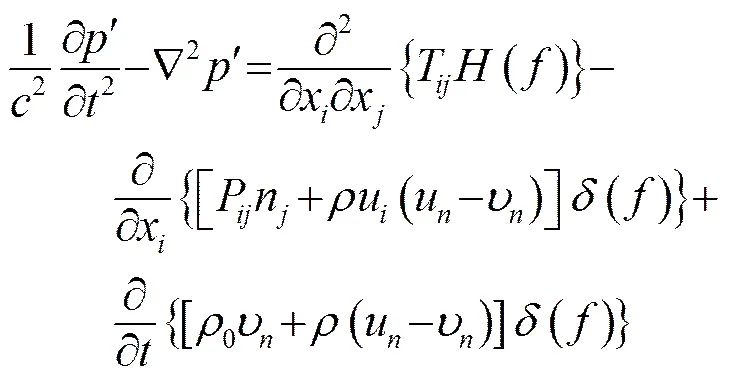
式中：u为流体在x方向的速度分量；u为垂直表面的流体速度分量；为x方向的表面速度分量；为垂直表面的速度分量；为Dirac Delta 函数；为赫维塞(Heaviside)函数；

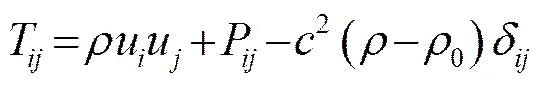
(3)

方程(1)是利用自由空间的格林函数(()/4p)得到的，完整的求解包含两次面积分和一次体积分。面积分后得到的是单极子、偶极子和部分四极子声源，体积分得到的是表面之外区域的空间四极子(体)声源。

1.2 计算实例

哈特曼发声器的结构如图1所示。单层哈特曼发声器阵列由两个面板组成，两个面板上分别设计了多个喷流口和谐振腔孔，两个面板用紧固件连接，喷流口和谐振腔孔正对并保持一定距离，如图2所示。两层哈特曼发生器阵列如图3所示。

建立哈特曼发声器阵列如图4和图5所示，模型参数如表1所示。图1中D为气流入口的直径，D为收缩喷口的直径，为气流入口到谐振腔口的距离，D为谐振腔入口直径，L为谐振腔的长度，cell为划分网格的最小面积。流体介质选择温度为300 K的理想气体，粘度为1.79×10-5kg/(m·s)。远距离监测点选择在出口外面离中心轴1 m的远距离，三点的坐标，单层为receiver1(6.26 mm，1000 mm)，receiver2(8.35 mm，1000 mm)，receiver3(10.44 mm，1000 mm)；两层为receiver1(0.84 mm，1000 mm)，receiver2(1.67 mm，1000 mm)，receiver3(3.34 mm，1000 mm)；三层为receiver1(5.01 mm，1000 mm)，receiver2(5.85 mm，1000 mm)，receiver3(6.68 mm，1000 mm)，receiver4(7.52 mm，1000 mm)。

表1 模型参数

计算过程中，首先利用大涡模拟法计算瞬态流场参数并捕捉声源数据，然后求解FW-H方程，得到监测点的声压信号，最后进行快速傅里叶变换进行频谱分析。对建立的模型进行大涡模拟计算，利用计算的音源数据求解FW-H方程得到监测点1的声压时程曲线如图6所示。对监测点1的声压信号进行FFT变换，可以得到频谱图，如图7、8所示，再对计算的数据进行频谱分析和声功率分析。本文计算中声压级的参考声压为2×10-5Pa。

2 哈特曼发声器阵列声场声强经验公式

以下采用FW-H声模拟法研究哈特曼发声器阵列的声场声强。通过研究不同入口气压条件下哈特曼发声器阵列的声场声压和声强，拟得出声场声强与声压和距离关系。计算了入口气压分别为3.12、4.12、5.12、6.12、7.12和8.12 atm的情况下，单层、两层和三层哈特曼发声器阵列1 m远的监测点的声压和声强。

表2为单层哈特发声器阵列的声强计算结果。表3为两层哈特曼发声器阵列的声强计算结果。表4为三层哈特曼发声器阵列的声强计算结果。

表2 单层哈特曼发生器阵列声强计算结果

3 结果分析

参照哈特曼发声器声功率经验公式=2.95D2×(c-0.93)1/2，设哈特曼发声器阵列声场声强(W/m2)近似服从如下经验回归方程：

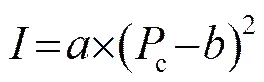
式(4)中：c为入口的绝对压强，单位atm；、为常数，由监测点的距离和哈特曼发声器的结构尺寸决定。依据入口气压分别为3.12、4.12、5.12、6.12、7.12和8.12 atm的哈特曼发声器阵列的1 m远的监测点的声压和声强的计算数据，进行回归分析，得出了不同距离场点的经验公式。

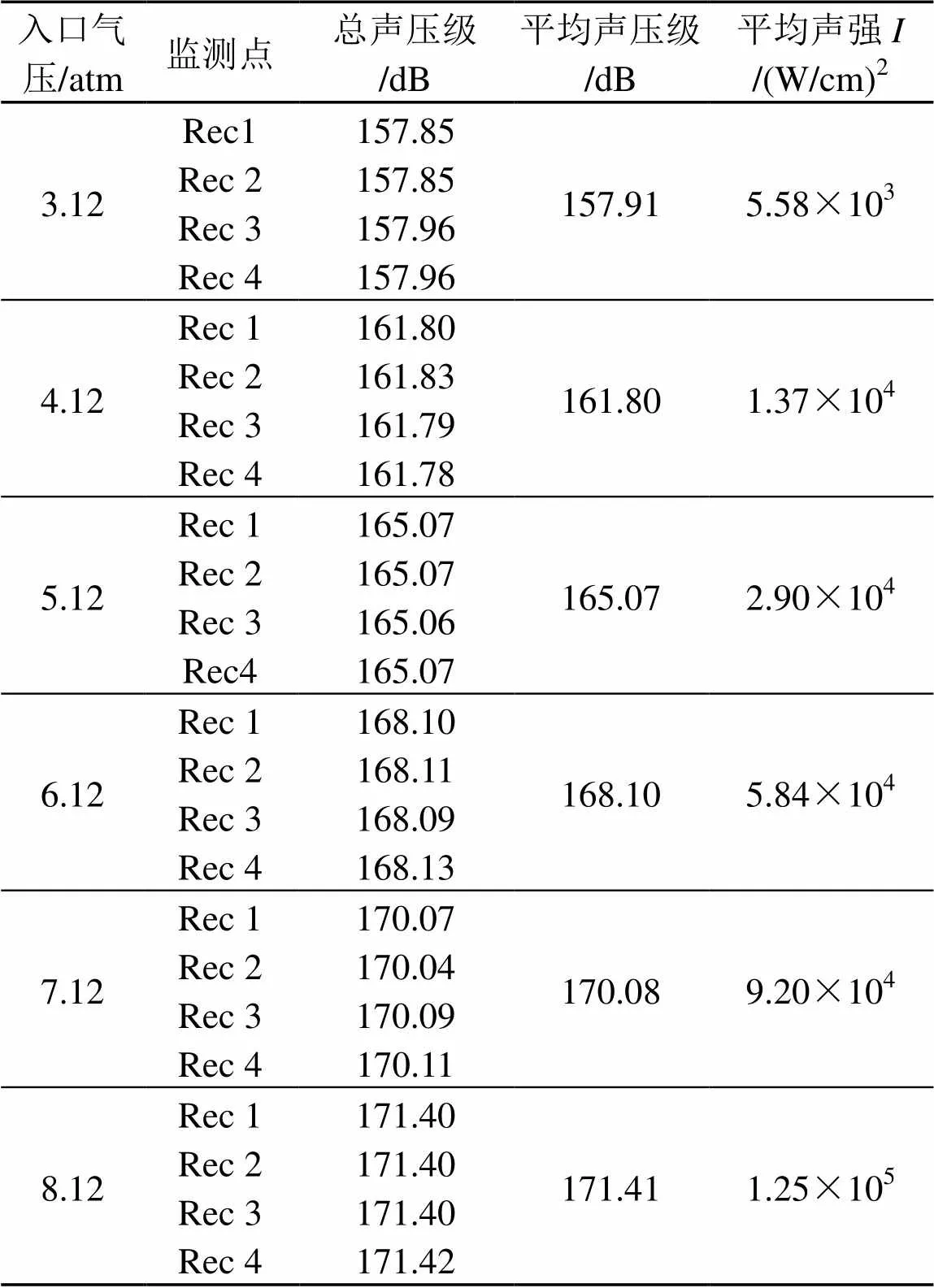
表3 两层哈特曼发生器阵列声强计算结果

对单层哈特曼发生器阵列所得数据进行回归分析，拟合曲线如图9所示。对回归进行方差分析和F分布检验如表5所示，回归结果在置信水平0.0004上可信，其回归水平显著，经验公式的可信度很高。同样对两层和三层计算结果进行回归分析，得出拟合曲线如图10和图11所示，对回归进行方差分析和F分布检验见表6和表7。方差分析显示两层和三层哈特曼发声器阵列声强回归曲线回归水平更显著，在0.0001以上可信，经验公式的可信度更高。

当入口气压与外界环境压力相等时，即c＝1 atm时，气流不能进入哈特曼发声器阵列，不能产生声音，因而声强为零，数据分析中增加了这对数据。实际分析中是对各阵列的7组数据进行回归分析，以下分析同。得出单层哈特曼发声器阵列1 m处监测点声强关于入口气压的经验方程为

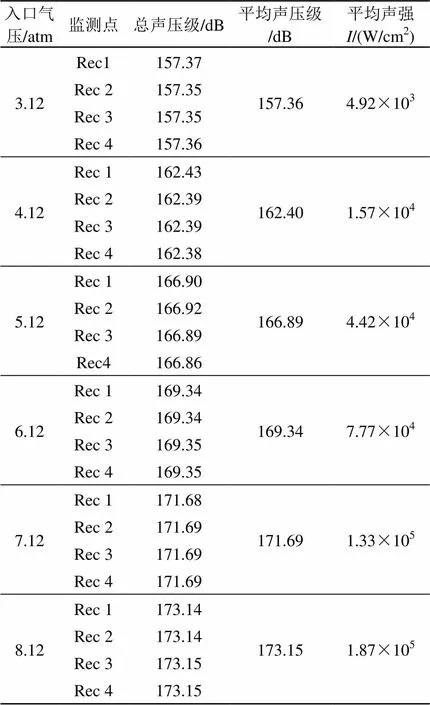
表4 三层哈特曼发生器阵列声强计算结果

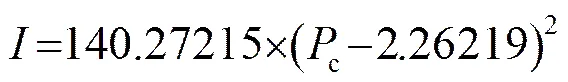
两层哈特曼发声器阵列1 m处监测点声强关于入口气压的经验方程为

(6)

三层哈特曼发声器阵列1 m处监测点声强关于入口气压的经验方程为

表5 单层阵列的经验公式的回归显著性分析

表6 两层阵列的经验公式的回归显著性分析

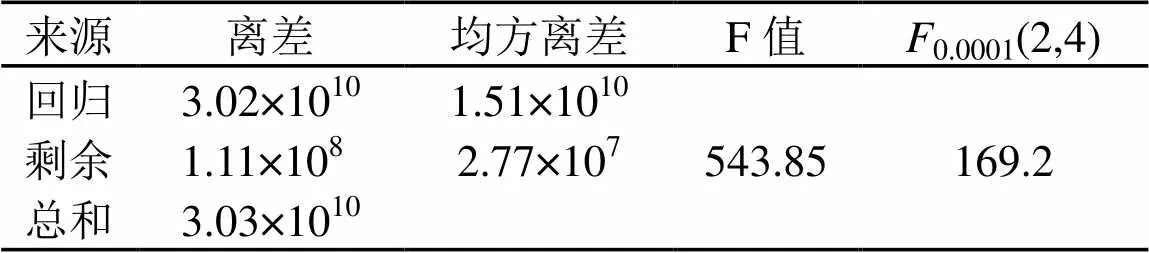
表7 三层阵列的经验公式的回归显著性分析

4 结论

利用FW-H声模拟法对哈特曼发声器阵列的声学特性进行了研究。研究了单层、两层和三层哈特曼发声器阵列的不同入口气压条件下声场声强，对计算结果进行了非线性回归分析，得出了哈特曼发声器阵列声场声强的经验公式。论文结论对哈特曼发声器阵列的应用具有重要的指导意义。

[1] Hartmann J, Trolle B. On a new method for the generation of sound wave[J]. Phys. Rev. 1922, 20: 719-727.

[2] Hartmann J, Trolle B. A new acoustic generator[J]. J Sci In str, 1927, 4(4): 101-111.

[3] Sprenger H. Ueber thermische Effekte in Resoanzrohern[J]. Fed Inst Tech Zurich, 1954, 21: 18-35.

[4] 谷嘉锦, 张强. 哈特曼发声器的实验研究[J]. 应用声学, 1992, 12(4): 17-19.

GU Jiajin, ZHANG Qiang. The Experimental Research of Hartmann Generator[J]. Applied Acoustics, 1992, 12(4): 17-19.

[5] CHEN Rensong, HE Bin. Design for a kind of high-power ultrasonic radiation pistol[J]. The Proceeding of the China Association for Science and Technology, Science Press, 2006, 3(4): 344-349.

[6] 陈仁松. 哈特曼发声器的声学特性研究[J]. 声学技术, 2012, 31(3): 335-339.

CHEN Rensong. Research on acoustic characteristics of Hartmann acoustic generator[J]. Technical Acoustics, 2012, 31(3): 335-339.

[7] 陈仁松. 中心棒哈特曼发声器声学特性研究[J]. 声学技术, 2013, 32(2): 195-163.

CHEN Rensong. Research on acoustic characteristics of Hartmann acoustic generator with central-stick[J]. Technical Acoustics, 2013, 32(2): 195-163.

[8] Brentner K S, Farassat F. An Analytical comparison of the acoustic analogy and kirchhoff formulations for moving surfaces[J]. AIAA Journal, 1998, 36(8): 1379-1386.

[9] Ffowcs-Williams J E, Hawkings D L. Sound generation by turbulence and surfaces in arbitrary motion. Proc. Roy. Soc. London, 1969, A264: 321-342.

Research on acoustic characteristics of Hartmann acoustic generator with central-stick

CHEN Ren-song, WANG Guo-qing, CHEN Xiu-hai, GAO Xin-jun, JIA Jun-bo, PEI Yong-quan

(The Shaanxi Province Baoji City 150Mailbox 11 Subbox 28Number, Baoji 721013, Shaanxi, China)

Based on the method FW-H acoustic model, the acoustic characteristics of the Hartmann acoustic generator array are numerically calculated for different inlet pressures of 3.12, 4.12, 5.12, 6.12, 7.12 and 8.12atm. The empirical equation of downstream acoustic intensity is introduced by nonlinear fitting of the calculated intensity results for different inlet pressures. The significance test is taken with F function, and the results show that the confidence level is at 10-4, and the regression level is high. The believability of the empirical equation of acoustic intensity is high. The results of the paper are significant for the practical application of the Hartmann acoustic generator array.

Hartmann ultrasonic generator array; the FW-H acoustic model; acoustic characteristics

TJ7

A

1000-3630(2015)-06-0484-05

10.16300/j.cnki.1000-3630.2015.06.002

2015-01-21;

2015-04-30

国家863计划课题项目(2005AA000200)。

陈仁松(1980－), 男, 山东潍坊人, 博士, 研究方向为超声波技术。

陈仁松, E-mail: chenrensong@163.com