基于全变分扩展方法的压缩感知磁共振成像算法研究
蒋明峰 刘 渊 徐文龙 冯 杰 汪亚明
基于全变分扩展方法的压缩感知磁共振成像算法研究
蒋明峰*①刘 渊①徐文龙②冯 杰①汪亚明①
①(浙江理工大学信息学院 杭州 310018)②(中国计量学院生物医学工程系 杭州 310018)
针对全变分算法在压缩感知磁共振成像(CS-MRI)重构过程中存在“阶梯效应”的问题,该文研究3种基于全变分扩展方法的CS-MRI成像算法,即高阶全变分、总广义变分和组合稀疏全变分,并将其与平移不变离散小波稀疏基相结合,建立稀疏模型,采用快速复合分裂算法求解CS-MRI重构的凸优化问题。同时,讨论了全变分及其扩展方法对两种不同磁共振图像数据和径向欠采样模式重构CS-MRI的精度。实验结果表明,基于全变分扩展的重构算法能有效解决全变分重建中存在阶梯效应的缺点;另外,相比高阶全变分和总广义变分重构算法,组合稀疏全变分方法具有更好的重建效果,获得更高重构信噪比。
磁共振图像;压缩感知;全变分扩展算法;组合稀疏
1 引言
随着临床各种应用领域的要求不断提高,需要尽可能地减少磁共振系统成像时间,进而减少长时间扫描过程中造成的运动伪影,提高磁共振成像质量。基于压缩感知理论的磁共振成像可以以远低于奈奎斯特采样的频率进行采样,并从这些欠采样数据中实现磁共振图像的重构,降低采样数据总量,缩短磁共振扫描时间,提高成像速度。只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解一个优化问题从这些少量的投影中以高概率重构出原信号。压缩感知(Compressed Sensing, CS)理论由Candès等人[1]和Donoho[2]提出,是一个充分利用信号稀疏性或可压缩性的全新信号采集、编解码理论。
全变分(Total Variation, TV)正则化模型是一种基于偏微分方程(PDE)的变分去噪模型,它是由Rudin等人于1992年提出来的,该方法被应用到全向图像稀疏重构[3],视频压缩感知重构[4],稀疏磁共振成像[5]等领域。但全变分在磁共振稀疏图像重构的应用中,常常出现“阶梯效应”,从而使得边缘的重建效果不够理想。基于全变分扩展的高阶全变分(Higher Degree Total Variation, HDTV)[6],总广义变分(Total Generalize Variation, TGV)[7],组合稀疏全变分(Group-Sparsity Total Variation, GSTV)[8]算法能够较好地克服去噪过程中的阶梯效应。本文将结合基于全变分扩展的方法和平移不变离散小波稀疏基讨论磁共振图像稀疏重构问题,利用径向欠采样轨迹[9]实现磁共振K空间数据的有效欠采样,然后采用快速复合分裂算法(Fast Composite Splitting Algorithm, FCSA)[10]解决磁共振稀疏重构凸优化问题。
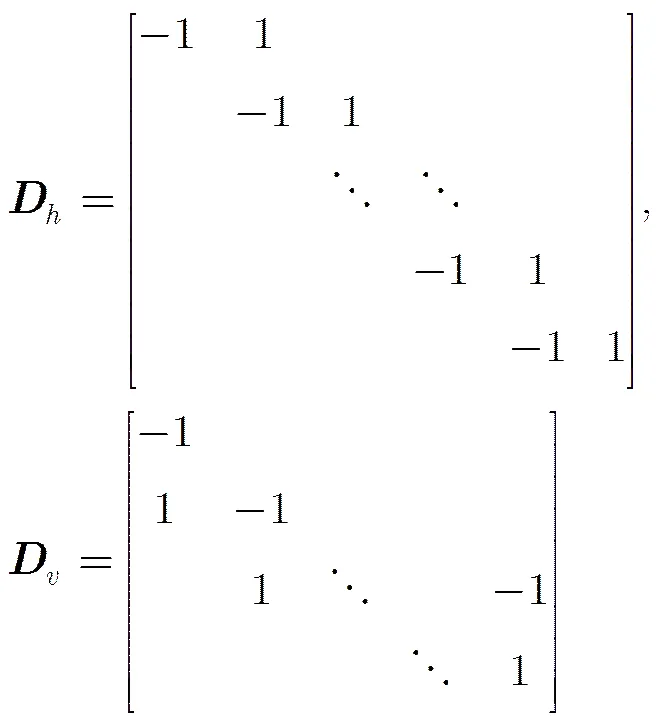
2 基于全变分扩展的压缩感知磁共振成像方法
基于全变分的压缩感知磁共振图像重构可以通过解决式(1)下面凸优化问题:
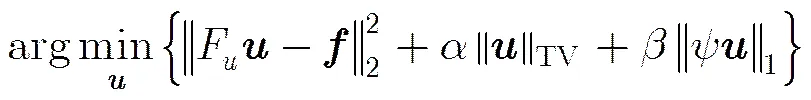
式中F是磁共振图像欠采样傅里叶变换算子,是获取K空间欠采样数据,是需重构的磁共振图像,是平移不变离散小波变换(SIDWT)稀疏基[11,12],和是正则化系数。在本文中采用结合基于全变分扩展的方法和平移不变离散小波稀疏基的方法,亦即在压缩感知磁共振图像重构的过程中采用全变差正则化约束项(式(1)中)和平移不变离散小波变换稀疏约束项(式(1)中)相结合的方法。全变分方法在稀疏磁共振图像重构过程中存在“阶梯效应”,该文将研究以全变分的扩展算法(HDTV, TGV, GSTV)替换全变换算法(TV)实现CS-MRI稀疏重构,重构更加准确的磁共振图像。
2.1 高阶全变分算法
高阶全变分(HDTV)模型[6],在原有的TV模型上添加了一个椭圆算子,使得重建过程中能够保留真实边缘的同时去除伪边缘,从而防止了边缘区域阶梯效应的产生。各向异性HDTV,惩罚因子定义为
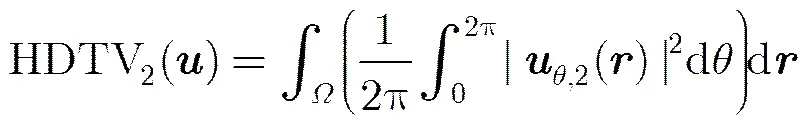

从式(2)可以看出,2维HDTV的惩罚因子保持着TV的重要特性,如:平移、旋转、协方差具有不变性等。在本文中采用=2。因此,基于高阶全变分的磁共振图像稀疏重构问题为
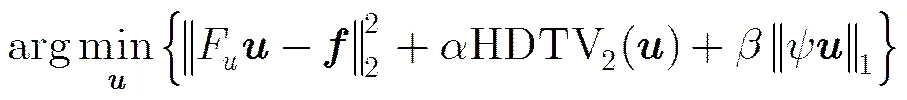
2.2 总广义变分模型
为避免图像重建过程中出现的阶梯效应将总广义变分(Total Generalized Variation, TGV)[7]的概念应用到CS-MRI成像算法中,TGV能够有效逼近任意阶的多项式函数,如:分段函数、分段仿射函数等。由于TGV具有凸的、旋转不变、下半连续等优良特性,有关TGV的研究正受到广泛关注。二阶TGV定义形式如式(5):

式中为需重构的磁共振图像,TGV 引入了辅助参数,并取。在该文的研究中设置,。因此,基于全变分的磁共振图像稀疏重构问题为
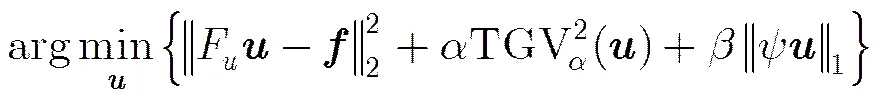
2.3 组合稀疏全变分模型
由于信号的微分具有组合稀疏特性,因此组合稀疏全变分方法(Group Sparsity Total Variation, GSTV)[8]最初被用于图像去噪。作为全变分的一种延伸,组合稀疏全变分方法具有TV所不具有的去噪能力。GSTV首先假设信号的微分具有结构性稀疏,表现为其一阶微分中数值较大的部分与其他大值部分相邻或相近,能够很容易地“被组合”在一起,这种方法可以有效地消除TV去噪过程中带来的阶梯效应。GSTV的“组合稀疏”特性能够将信号的微分自然分组,并且每组中也具有组合稀疏的特性。

其中,为图像像素在两个维度方向上的指数,该图像在k, k方向上的一阶微分分别为
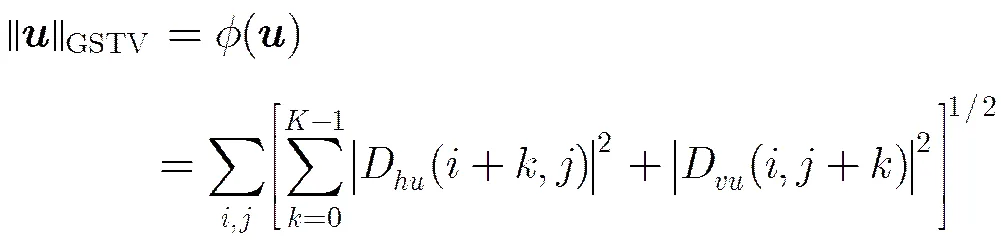
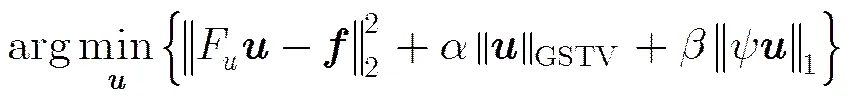
3 基于快速复合分裂算法的磁共振图像稀疏重构
将全变分及其扩展方法的正则化项统一简称为All-TV,对于式(1)、式(4)、式(6)、式(10)稀疏重构的复合正则化问题,快速复合分裂算法(FCSA)[10]将其分解成两个子问题:
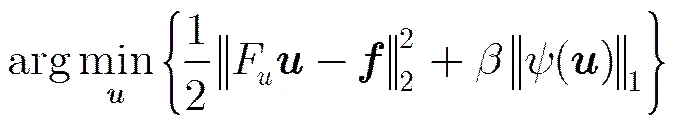

对于L1稀疏变换子问题(式(11)),利用快速迭代收缩阈值算法(FISTA)[13]能得到有效的解决,FISTA算法在图像重建的每一次迭代中为目标函数的线性化微分部分构造正则化,将L1子问题分解:
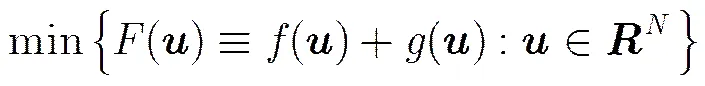

对于全变分及其扩展方法的子问题式(12),将其分解成两部分:

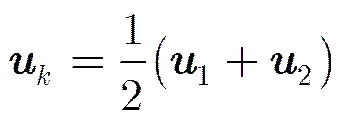
并将每次迭代的结果进行归一化处理,如式(17)所示:
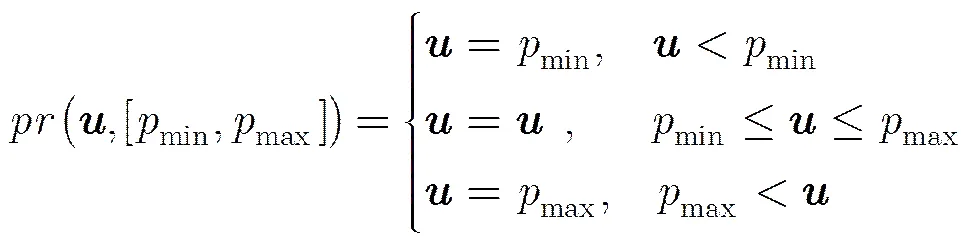
在该文的研究中设置min=0,max=255。
4 仿真与分析
该文采用两种磁共振图像:Shepp-Logan计算机仿真磁共振图像和心脏磁共振图像[16]来验证基于全变分扩展算法实现磁共振图像稀疏重构的性能。图1为Matlab库函数Phantom生成的Shepp-Logan图像及其局部放大图,图2为实际的3维动态磁共振心脏图像的第10帧图像及其局部放大图。本文采用径向欠采样模式实现磁共振K空间数据的欠采样,如图3所示,其加速因子为6。
为了评价图像重建的效果,该文采用信噪比(Signal-to-Noise Ratio, SNR)作为图像重建的评价指标,同时将重构图像和局部放大图作为重建效果的视觉评价标准。将全采样重构的图像作为金标准,记为(0),基于欠采样的磁共振稀疏重构图像为(),则SNR可以通过式(18)计算:
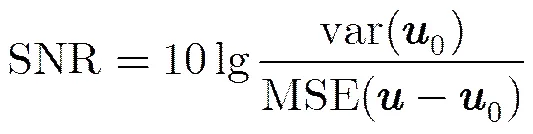
式中,MSE是重构图像()与全采样图像(0)之间的平均均方误差,var(0)为0的方差。
4.1 Shepp-Logan磁共振图像重构结果分析
在不同加速因子情况下,对全变分及其扩展算法实现稀疏重构欠采样的Shepp-Logan磁共振图像的性能进行分析比较。图4为分别采用基于TV, HDTV, TGV和GSTV稀疏重构的磁共振图像及其局部放大图,采样的加速因子为6(即采样率为16.7%)的径向采样轨迹,从图像重构的效果可以看出,采用全变换方法的重构结果能够基本保留图像的纹理特征,但边缘处较模糊,发生震荡,并且图像有类马赛克的块状现象,而基于全变分扩展的HDTV, TGV和GSTV方法能够有效地消除这一现象,重建后的图像纹理清晰、平滑,并且在这些扩展方法中,基于GSTV方法的重构质量最佳,重构磁共振图像边界清晰,其次为TGV方法的重构质量。
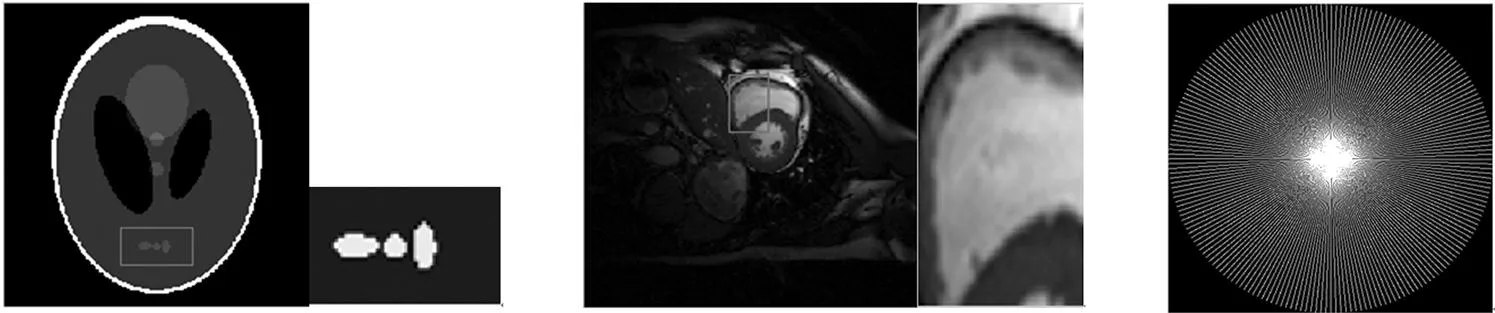
图1 shepp-logan磁共振 图2 心脏磁共振图像 图3 径向欠采样轨迹,
图像及其局部放大图 及其局部放大图 加速因子为6
4.2 心脏磁共振图像重构结构分析
该文对全变分及其扩展算法对心脏磁共振图像的稀疏重构性能进行分析和比较,心脏磁共振图像是由1.5T Philips核磁共振系统获得的[16],心脏磁共振图像边缘较多,结构组成较复杂。
图5为全变分及其扩展方法的重构心脏磁共振图像及其局部放大图,依次为TV方法、HDTV方法、TGV方法和GSTV方法,同样采用加速因子为6的径向采样轨迹,从图像重建的局部放大图可以看出,TV方法的重建结果轮廓不是很清晰,而且有较为明显的伪影出现,类马赛克的块状图像较为严重。基于全变分扩展的方法有效地解决了这种“阶梯效应”,而在3种全变分扩展方法中,基于GSTV方法的重建图像结果纹理清晰、光滑、自然,最接近全采样重构的金标准图像,其重构图像效果在所有方法中是最佳的。
图6为全变分及其扩展方法在不同的加速因子下的重构心脏磁共振图像的信噪比值,基于全变分扩展的重构方法信噪比要优于基于全变分的重构结果,而在所有重建方法中,基于GSTV方法重构图像的信噪比性能明显优于其它方法,这表明在任何加速因子条件下,GSTV能够重构更加准确的磁共振图像。
图7为心脏磁共振图像衰减因子分别为4和6的径向采样方式下GSTV组合因子值从1到10时的图像重建信噪比值,从图中可以看出,值选取为6时图像重建效果较好。而在重构Shepp-Logan磁共振图像时,GSTV方法选取值为5的磁共振图像重构效果最好。因此,最优值的选取,可能受到图像类型、图像分辨率等因素的影响,如何快速准确地选取最优值,将是以后研究的重点。

图4在加速因子为6时,基于全变分及其扩展方法重构Shepp-Logan磁共振图像及其局部放大图

图5在加速因子为6时,基于全变分及其扩展方法的重构心脏磁共振图像及其局部放大图

图6 不同加速因子下,全变分及其扩展方法重构心脏磁共振图像的信噪比 图7在加速因子为4, 6时,GSTV方法在不同组合因子K值下重构心脏磁共振图像信噪比
5 结束语
本文针对全变分算法在磁共振图像稀疏重构过程中存在阶梯效应的问题,讨论了3种基于全变分扩展的磁共振图像稀疏重构方法,即:HDTV, TGV和GSTV,将其与平移不变离散小波稀疏基相结合,建立稀疏模型,并采用快速复合分裂算法求解磁共振图像稀疏重构的凸优化问题。实验结果表明,3种全变分扩展算法能够有效消除全变分在CS-MRI图像重构过程中的阶梯效应,提高磁共振图像重构的精度。3种全变分扩展算法中,在任何加速因子情况下,基于GSTV方法重构的磁共振图像具有更高的信噪比,其重构的图像结果纹理清晰、边缘光滑。
[1] Candès E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.
[2] Donoho D L. Compressed sensing[J]., 2006, 52(4): 1289-1306.
[3] 娄静涛, 李永乐, 谭树人, 等. 基于全变分的全向图像稀疏重构算法[J]. 电子学报, 2014, 44(2): 243-249.
Lou Jing-tao, Li Yong-le, Tan Shu-ren,Sparse reconstruction for omnidirectional image based on total variation[J].,2014, 44(2): 243-249.
[4] 李然, 干宗良, 崔子冠, 等. 联合时空特征的视频分块压缩感知重构[J]. 电子与信息学报, 2014, 36(2): 285-292.
Li Ran, Gan Zong-liang, Cui Zi-guan,.. Block compressed sensing reconstruction of video combined with temporal-spatial characteristics[J].&2014, 36(2): 285-292.
[5] Lustig M, Donoho D L, and Pauly J M. Sparse MRI: the application of compressed sensing for rapid MR Imaging[J]., 2007, 58(6): 1182-1195.
[6] Hu Y and Jacob M. Higher Degree Total Variation (HDTV) regularization for image recovery[J]., 2012, 21(5): 2559-2571.
[7] Guo W, Qin J, and Yin W. A new detail-preserving regularity scheme[J]., 2014,7(2): 1309-1334.
[8] Selesnick I W and Chen P. Total variation denoising with overlapping group sparsity[C]. IEEE International Conference Acoust, Speech, Signal Processing (ICASSP), Vancouver, Canada, 2013: 1-5.
[9] Zhang S, Block K T, and Frahm J. Magnetic resonance imaging in real time: advances using radial FLASH[J].2010, 31(1): 101-109.
[10] Huang J, Zhang S, and Metaxas D. Efficient MR image reconstruction for compressed MR imaging[J]., 2011, 15(5): 670-679.
[11] Ning B, Qu X, Guo D,.. Magnetic resonance image reconstruction using trained geometric directions in 2D redundant wavelets domain and non-convex optimization[J].2013, 31(9): 1611-1622.
[12] Qu X, Hou Y, Lam F,.. Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator[J]., 2014, 18(6): 843-856.
[13] Jiang M , Jin J, Liu F,. Sparsity-constrained SENSE reconstruction: an efficient implementation using a fast composite splitting algorithm[J]., 2013, 31(7): 1218-1227.
[14] Figueiredo M, Bioucas-Dias J, and Nowak R. Majorization minimization algorithms for wavelet-based image restoration[J]., 2007, 16(12): 2980-2991.
[15] He B, Liao L Z, Han D,.. A new inexact alternating directions method for monotone variational inequalities[J]., 2002, 92(1): 103-118.
[16] Jung H, Ye J C, and Kim E Y. Improved k-t BLAST and k-t SENSE using FOCUSS[J]., 2007, 52(11): 3201-3226.
The Study of Compressed Sensing MR Image Reconstruction Algorithm Based on the Extension of Total Variation Method
Jiang Ming-feng①Liu Yuan①Xu Wen-long②Feng Jie①Wang Ya-ming①
①(,,310018,)②(,,310018,)
The Total Variation (TV) method is often used to reconstruct the Compressed Sensing Magnetic Resonance Imaging (CS-MRI), however, it can generate the “stair effect” in the reconstructed MR image. In this paper, there types of TV extension based methods, i.e. High Degree Total Variation (HDTV), Total Generalize Variation (TGV) and Group-Sparsity Total Variation (GSTV), are proposed to implement the sparse reconstruction of MR image. In addition, the shift-invariant discrete wavelet transform are integrated into these TV extension based methods as the sparsifying transform. The Fast Composite Splitting Algorithm (FCSA) is adopted to solve the convex optimization problem of CS-MRI reconstruction. And the Two different types of MR images with radial sampling trajectory are used to validate the reconstruction performance of CS-MRI by using the TV extension methods. The experiment results show that the TV extension based models can overcome the shortcomings of TV based model. Moreover, compared with HDTV and TGV methods, the GSTV method can obviously improve the reconstruction quality with higher Signal-to-Noise Ratio (SNR).
Magnetic Resonance Imaging (MRI); Compressed Sensing(CS); Total Variation (TV) extension method; Group-sparsity
R445.2
A
1009-5896(2015)11-2608-05
10.11999/JEIT150179
2015-02-02;改回日期:2015-06-01;
2015-07-17
蒋明峰 m.jiang@zstu.edu.cn
国家自然科学基金(61272311);浙江省自然科学基金(LY14F010022, LZ15F020004);浙江省科技厅公益项目(2013C31021, 2015C31075);浙江省科技厅国际科技合作研究项目(2013C24019);浙江省‘仪器科学与技术’重中之重学科开放基金;浙江理工大学521人才培养计划
The National Natural Science Foundation of China (61272311); Natural Science Foundation of Zhejiang Province (LY14F010022, LZ15F020004); Science Technology Department of Zhejiang Province (2015C31075, 2013C24019); Zhejiang Key Discipline of Instrument Science and Technology; The 521 Talents Project of Zhejiang Sci-Tech University
蒋明峰: 男,1977年生,副教授,博士,硕士生导师,研究方向为计算机医学图像处理、生物医学信号处理.
刘 渊: 男,1991年生,硕士生,研究方向为计算机图像处理.
徐文龙: 男,1972年生,教授,博士,硕士生导师,研究方向为生物医学信号处理、磁共振图像处理.
冯 杰: 男,1980年生,讲师,博士,研究方向为视频图像处理.
汪亚明: 男,1972年生,教授,博士,博士生导师,研究方向为 模式识别、图像处理.

