内壳层电子激发诱发的电子波函数的弛豫效应
李继弘,彭昌宁,张耀文,赵金雄
内壳层电子激发诱发的电子波函数的弛豫效应
*李继弘,彭昌宁,张耀文,赵金雄
(陇东学院电气工程学院,甘肃,庆阳 745000)
利用电子关联效应和相对论效应的Hartree-Fock(HFR)自洽场方法(SCF),计算了Kr原子在基态4p6和激发态1s-15s,2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,4p-15s情况下的各壳层电子的轨道半径、有效量子数、束缚能及径向波函数,系统地研究了内壳层电子激发导致的电子波函数的弛豫现象。结果表明,对于同一电子轨道,越是内壳层电子激发,驰豫效应的影响越明显;对于同一激发态,驰豫效应对较外壳层电子的影响要大于对较内壳层电子的影响。
弛豫效应;轨道半径;波函数;HFR自洽场方法
0 引言
弛豫效应是指当某一壳层中的电子被激发或电离后引起的其余电子的重排现象[1-3]。研究表明[4-8],对于具有满壳层结构的原子(或离子),当最外层电子被激发(或电离)时,其它电子的重排会引起各壳层电子的初、末态波函数发生明显的变化,并对跃迁能、跃迁振子强度和跃迁概率的精确计算产生重要影响。所以近几年,系统研究复杂原子的结构和性质的理论和方法中都考虑了弛豫和相关效应[9-11]。在大量的复杂原子的物理过程中,除了原子(或离子)最外层电子的激发和电离外,往往同时伴有内壳层电子的激发和电离。因此,系统地研究内壳层电子激发或(电离)引起的电子波函数的弛豫效应,对于人们深入地理解复杂原子的结构和性质有着重要的意义。基于此,本文以具有稳定闭壳层结构的原子Kr为例,系统研究不同内壳层电子激发时引起的弛豫效应及其变化规律。研究中选取Kr原子的基组态以及从不同内壳层1s,2s,2p,3s,3p,3d,4s和4p激发一个电子到5s壳层时形成的8种激发态,即:1s22s22p63s23p63d104s24p6(简记为4p6),1s2s22p63s23p63d104s24p65s(简记为1s-15s), 1s22s2p63s23p63d104s24p65s(简记为2s-15s), 1s22s22p53s23p63d104s24p65s(简记为2p-15s), 1s22s22p63s3p63d104s24p65s(简记为3s-15s), 1s22s22p63s23p53d104s24p65s(简记为3p-15s), 1s22s22p63s23p63d94s24p65s(简记为3d-15s), 1s22s22p63s23p63d104s4p65s(简记为4s-15s), 1s22s22p63s23p63d104s24p55s(简记为4p-15s)。
1 理论方法
1.1 径向波函数及能级的计算
考虑了电子关联效应和组态相互作用的HFR理论方法的详细描述可以参阅文献[12],这里仅作扼要介绍。在Hartree-Fork理论中,组态平均下计算电子径向波函数可以用自洽场迭法求解相对论性的Hartree-Fork方程式[11]得到:

(1)
在(2)式中,
(3)

(5)
1.2 轨道半径的计算

1.3 有效量子数的计算
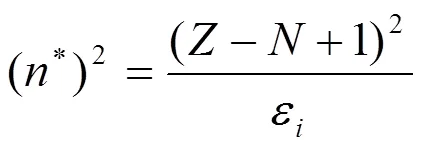
式中是核电荷数,代表核外电子数。
2 结果与讨论
2.1 弛豫效应对平均轨道半径的影响
表1是当前计算的Kr原子在基态4p6和各激发态1s-15s, 2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,4p-15s情况下各壳层电子的平均轨道半径。比较数据可以看出,不同激发态对应的同一轨道(譬如不同激发态下的4p轨道)的平均半径明显不同。总的来说,对于同一轨道,在各种激发态情况下的轨道半径要小于在基态情况下的轨道半径,这说明,内壳层电子激发时诱发的驰豫效应使得电子轨道收缩了。以基态为基准,比较各激发态情况下同一轨道对应的电子轨道平均半径与基态情况下的电子轨道平均半径的偏差,可以看出,越是内壳层电子被激发,上述偏差越大。例如,对于同一电子轨道4p的平均半径,在激发组态1s-15s时比在基态4p6时减小了11%,偏差最大;依次是2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,而在4p-15s时比在基态4p6时减小了5%,偏差最小。这说明越是内壳层电子激发,电子轨道平均半径的收缩越大,即越是内壳层电子激发诱发的驰豫效应对电子平均轨道半径的影响越大;另外,从表中数据还可以看出,驰豫效应对不同电子轨道的影响也不同。比如,比较基态4p6和各种激发态1s-15s, 2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,4p-15s情况下的1s,2s,2p,3s,3p,3d,4p等电子轨道的平均半径的变化可以发现,1s轨道的变化最小,而2s,2p,3s,3p,3d,4s,4p轨道的变化依次增大,在4p轨道时这种变化最大。这表明,驰豫效应对较外层的电子轨道平均半径的影响要大于较内壳层。

表1 Kr原子在基态和各激发态情况下各壳层电子的轨道平均半径(单位:原子单位)
2.2 弛豫效应对束缚能和有效量子数的影响
表2和表3分别是Kr原子在基态4p6和各激发态1s-15s, 2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,4p-15s情况下各壳层:1s,2s,2p,3s,3p,3d,4s,4p电子的束缚能和有效量子数。从这些数据也能说明:对于同一电子轨道,越是内壳层电子激发,驰豫效应的影响越明显,同时对于同一激发态,驰豫效应对较外层的电子的影响要大于对较内壳层电子的影响。例如,在表2中,对于同一电子轨道4p电子,在1s-15s激发态的束缚能较在基态4p6的束缚能改变了51.7%,相对于基态变化最大,而在4p-15s激发态较在基态束缚能改变了35.8%,相对于基态变化最小;同样在表3中,对于同一电子轨道4p电子,在1s-15s激发态的有效量子数比在基态4p6的有效量子数改变了18.8%,相对于基态变化最大,而在4p-15s激发态比在基态有效量子数改变了14.2%,相对于基态变化最小。所以,越是内壳层电子激发,电子重排的影响越大。对于同一激发态(比如1s-15s激发态),比较1s,2s,2p,3s,3p,3d,4s,4p轨道电子的束缚能(表2)和有效量子数(表3)相对于基态的变化可以发现,1s轨道的变化最小,而2s,2p,3s,3p,3d,4s,4p的变化依次增大,在4p轨道时变化最大。

表2 Kr原子在基态和各激发态情况下各壳层电子的束缚能(单位:原子单位)

表3 Kr原子在基态和各激发态情况下各壳层电子的有效量子数
2.3 弛豫效应对电子波函数的影响
图1(a)-(h)进一步展示了Kr原子的基态和不同内壳层电子被激发到5s后(即4p6、1s-15s、 2s-15s、2p-15s、3s-15s、3p-15s、3d-15s、4s-15s和4p-15s九种激发态情况下)的1s,2s,2p,3s,3p,3d,4s和4p电子轨道的径向波函数。从图可以看出,对于同一轨道,不同壳层电子激发引起了该电子径向波函数的峰值(即概率密度最大值)位置相对于基态发生了向左移动,但对于不同电子轨道,左移的程度表现出规律性的不同:4p-15s 激发态的波函数的峰值与基态4p6情况下的波函数的峰值离得最近(即左移程度最小),4s-15s 次之,依次是3d-15s、3p-15s、3s-15s、2p-15s、2s-15s,而1s-15s激发态的波函数的峰值与基态的峰值离得的最远。这说明,离原子核越近的壳层电子激发,驰豫效应对其它电子波函数的影响越大。另外,从图还可以看出,驰豫效应对不同轨道的电子波函数的影响是:对1s轨道(图1(a)),在各种激发态与基态情况下的概率密度分布的差别最小,而在2s、2p、3s、3p、3d、4s轨道上这种差别依次增大,在4p轨道(图1(h))上这种差别最为明显。这说明,弛豫效应对外壳层电子轨道波函数的影响要比内壳层大。
Fig .1 The radial wave function of each shell electrons in the ground states and excited states in Kr
4 结论
本文利用相对论性的Hartree-Fork(HFR)自洽场方法,计算了Kr原子在基态4p6和激发态1s-15s,2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s,4p-15s情况下的1s,2s,2p,3s,3p,3d,4s和4p壳层电子的轨道半径、束缚能、有效量子数及径向波函数,系统地研究了内壳层电子激发导致的电子波函数的弛豫现象。结果说明,对于同一电子轨道,越是内壳层电子激发,驰豫效应的影响越明显,同时对于同一激发组态情况下,驰豫效应对较外层的电子的影响要大于对较内壳层电子的影响。
参考文献:
[1] 罗月娥,董晨钟,颉录有,等. Xe原子的等核及等电子系列离子径向波函数的性态研究[J].原子与分子物理学报, 2008, 25(1): 25-33.
[2] 李继弘,彭昌宁,张耀文.内壳层电子激发诱发的电子波函数的塌缩现象[J].陇东学院学报:自然科学版, 2014, 25(3): 11-12.
[3] 李继弘,张耀文,彭昌宁.d、f电子过渡族原子的理论计算[J].井冈山大学学报:自然科学版,2014,35(3):22-26.
[4] 李继弘.4d波函数塌缩对类Kr离子4p64p5nd辐射跃迁性质影响研究[J].四川大学学报:自然科学版,2013,50(6):1277-1284.
[5] 李继弘,杨宁选,董晨钟.Rn原子的等电子系列离子5f电子径向波函数的性态研究[J].原子与分子物理学报,2011,28(4): 618-624.
[6] Grant I P, McKenzie B J, Norrington P H, et al. An atomic multiconfigurational Dirac-Fock package[J]. Computer Physics Communications, 1980, 21(2): 207-231.
[7] Parpia F A, Fischer C F, Grant I P. GRASP92: A package for large-scale relativistic atomic structure calculations[J]. Computer physics communications, 1996, 94(2): 249-271.
[8] Dong C Z, Fritzsche S, Xie L Y. Energy levels and transition probabilities for possible X-ray laser lines of highly charged Ni-like ions[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2003, 76(3): 447-465.
[9] Grant I P. Gauge invariance and relativistic radiative transitions[J]. Journal of Physics B: Atomic and Molecular Physics, 1974, 7(12): 1458.
[10] 颉录有,董晨钟,周效信,等.延迟和相关效应对Ne原子2p53s1,3P10-2p61S0跃迁的影响 [J].原子与分子物理学报,2002,19(1): 54-54.
[11] Dong C Z, Fritzsche S, Fricke B. Theoretical study of the 5p56s–5p6spectra of neutral xenon[J]. The European Physical Journal D-Atomic, Molecular, Optical and Plasma Physics, 2006, 40(3): 317-323.
[12] Cowan R D. The Theory of Atomic Structure and Spectra [M]. Berkeley .Los Angeles. London:University of California Press, 1981, 229-234.
EFFECT OF RELAXATION INDUCED BY EXCITATION OF INNER SUBSHELL ELECTRONS ON THE WAVE FUNCTION
*LI Ji-hong,PENG Chang-ning,ZHANG Yao-wen,ZHAO jin-xiong
(Electrical Engineering College ,Longdong University, Qingyang, Gansu 745000, China)
Self-consistent-field calculations of the orbital radii and binding energy and radial wave function of the subshell electrons in the ground state 4p6and eight excited state 1s-15s,2s-15s,2p-15s,3s-15s,3p-15s,3d-15s,4s-15s, and 4p-15s in Krypton have been made by using relativistic Hartree-Fork(HFR). The relaxation effects induced by excitation (or ionization) of inner subshell electrons and their influences on the electronic wave functions have been systematically studied. The experiment and analysis shows that that the more inner-shell electron is excited, the effects of relaxation is more obvious. In the sameexcitation state, the influence of the relaxation effects on theouterelectronis greater thanthe inner-shellelectrons.
relaxation effects; orbital radii; wave function; HFR self-consistent field method
1674-8085(2015)01-0034-06
O562.1
A
10.3969/j.issn.1674-8085.2015.01.007
2014-07-21;修改日期:2014-11-18
庆阳市自然科学基金项目(ZJ201306)
*李继弘(1969-),女,甘肃庆阳人,教授,硕士,主要从事原子结构与原子光谱研究(E-mail:ldxyljgh@163.com);
彭昌宁(1965-),男,甘肃正宁人,副教授,主要从事理论物理教育教学研究(E-mail: qypcn@tom.com);
张耀文(1981-),女,甘肃庆阳人,讲师,硕士,主要从事强激光场与物质相互作用研究(E-mail:jee@mail.ustc.edu.cn);
赵金雄(1991-),男,甘肃环县人,硕士生,主要从事纳米电子研究(E-mail: 18919271240@163.com).

