基于Hash算法的DNA序列k-mer index问题的数学建模

郭方舟，华阳，董修伟，蔡志丹

（长春理工大学　理学院，长春　130022）

基于Hash算法的DNA序列k-mer index问题的数学建模

郭方舟，华阳，董修伟，蔡志丹

（长春理工大学理学院，长春130022）

针对查找DNA序列的相似序列问题，给出了建立索引和查找索引的数学模型，基于Hash算法，建立了依赖于k值大小的顺序索引模型和散列索引模型，特别对较大k值选用了DJBHash函数，有效的避免了Hash冲突问题。最后在硬件平台CPU为2.6GHz、内存为8G、操作系统为64位Windows 7的条件下，对100万条长度为100的DNA序列进行了测试，给出了不同k值下建立和查询索引的用时和占用内存情况，有效的解决了DNA序列的k-mer index问题。

Hash算法；索引问题；数学模型；复杂度分析

从大量的DNA序列中查询相似序列是当前研究的热点问题。

所谓DNA序列的k-mer，指的是一条长度为k 的DNA子序列，由A、T、C、G四种字符组成。使用长度为k的窗口在一条DNA序列上依次滑动，可以得到该DNA序列的k-mer集合。而k-mer index问题就是对这些k-mer构建一种数据索引方法，以便之后可以对某条k-mer进行快速访问，获取其频次、位置等信息。

理想的索引方法是不经过比较，直接从字典中得到检索的关键字法。Hash算法的基本思想就是在元素的关键字与元素的存储位置之间确立一种函数关系，查找时直接得到元素的存储位置。所有元素的存储位置构成Hash表。在理想情况下，使用Hash表查找能达到O（1）的性能。

1　Hash算法简述

1.1Hash算法原理

Hash算法的基本原理［1，2］是：以关键字key为自变量，构造一个关键字与存储地址之间的函数，称Hash函数

H（x）为关键字key的存储地址，或称索引值。所有索引值构成一张Hash表，也称索引。实际情况中，可以直接将k-mer作为关键字，也可以先对其处理后再作为关键字。

理想情况下，不同关键字的索引值都不相同。但实际情况中，很难找到这样一个Hash函数。由此存在一个问题：两个关键字可能映射到同一个地址上。这种情形称为发生了“冲突（Collision）”，如图1所示，用1个Hash函数将key映射到Hash表中：k3和k4发生了冲突。

Hash表是算法为了在查找时间上更高效，而在空间上做出让步的一种存储的经典算法。如果没有时间限制，那么直接将关键字顺序存储，查找时遍历即可。显然，当数据量极大时，时间上是不允许的。另一方面，使用Hash函数生成的往往是一个相对随机的索引值，于是为了尽量减小冲突，需要构造一个庞大的空间来存储Hash表，因为不知道哪些位置会被使用。此时，难免出现无效的索引位置。

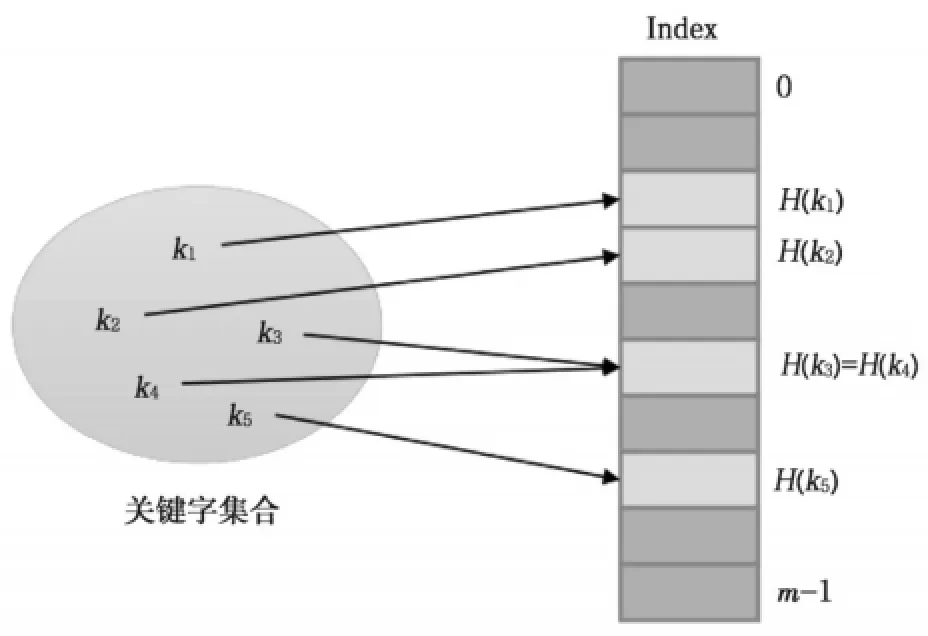
图1　用一个Hash函数将key映射到Hash表中：k3和k4发生了冲突

1.2“冲突”的处理

处理Hash冲突的方法很多［3］，如线性探测法、二次探测法、伪随机探测法、链地址法等方法。而这些方法中或处理复杂、或可能发生“二次冲突”。链地址法更适合解决本问题引起的Hash冲突。

所谓链地址法［5］，即把所有发生冲突的关键字都链接在Hash表的同一个地址之后。基于链地址法的Hash表实现简单，在对key的顺序信息不重要的应用中（如本问题），它可能是最快也是使用最广泛的冲突解决方法［2］。如图2所示，通过链地址法解决碰撞。

2　Hash算法在本问题中的应用

2.1该问题的特殊性

DNA序列有其特殊性，它仅由A、T、C、G四种字符构成。对k-mer而言，其总组合数为4k种。当k值较小时，大小的数组空间是可以接受的。此时可以不再使用传统的Hash函数，转而构造一个新的映射关系，将k-mer映射为连续的索引值，可以大幅度提升空间利用率，减小内存的使用。

另一方面，对于k值较大的情况，特定DNA序列的k-mer集合只是所有k-mer组合的一个小子集。此时，可以使用传统的Hash函数，只对出现过的k-mer计算其索引值。

2.2Hash函数的构造

一个优秀的Hash函数应该易于计算并能跟尽可能的减小冲突［6］。基于这个要求，加之这个问题的特殊性，最简单易行的方法就是将k-mer转化为一个4进制数，相应的函数表达式如下：

其中

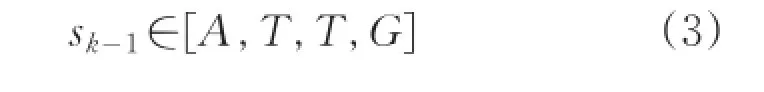
表1　不同Hash函数的冲突率

对于k值较大的情况，我们比较了常见的用于转换字符串的Hash函数［4］，选择了效果最好的DJB Hash函数。如表1所示，记录了不同Hash函数的冲突率。

2.3数据结构

两种情况所使用的数据结构有些不同，由于使用4进制函数时，可以逆向获得相应的k-mer，因此在存储时只需存储位置信息，而不需要存储相应的k-mer，大大减小的内存的使用。如图4所示，用于k值较小时顺序索引模型的数据结构，图5为k值较大时散列索引模型的数据结构。

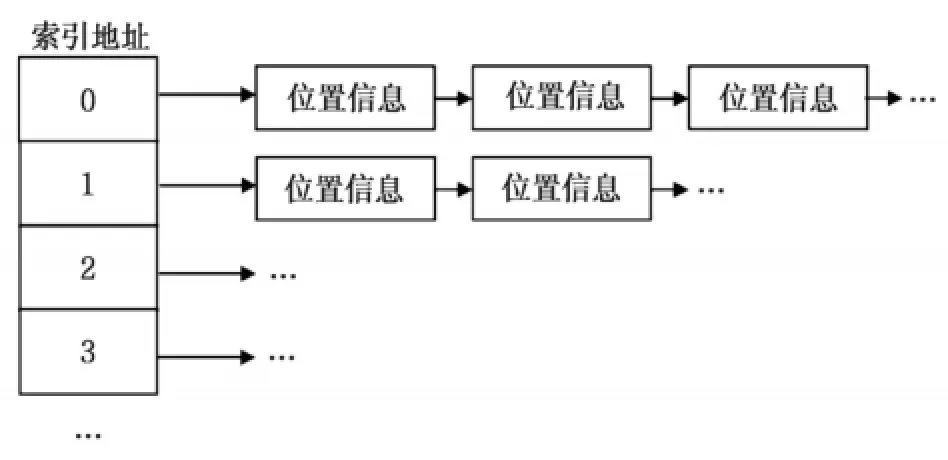
图3　用于k值较小时顺序索引模型的数据结构

图4　用于k值较大时散列索引模型的数据结构

2.4Hash表的大小

选择适当的数组大小，既不会因空位置过多而浪费内存空间，也不会因链表太长而降低查询效率［7］。如果存入的key多于预期，查找的时间会稍长；如果少于预期，虽然浪费了部分空间，但查找很快。

对该问题，k值较小时，数组大小即4k；当k较大时，如果事先知道待建索引的DNA序列的总长和k的大小，可以计算出k-mer的总数（包括重复）［8］。那么可以建立一个比该值稍小的数组。如果内存有限，则可以动态调整数组的大小以保持较短的链表，而且无需重写代码，适当调整参数即可。

2.5复杂度分析

建立索引的过程就是扫描一遍DNA序列的过程，时间复杂度为O（n）［9］。

如果使用的Hash函数能够大致均匀的将key分布于［0，M-1］，则查询的时间复杂度为O（m）=O （1），其中m＜N/M，N为key的数量，M为链的数量，简单证明如下：

由二项分布可知，对给定链含有q个key的的概率为：

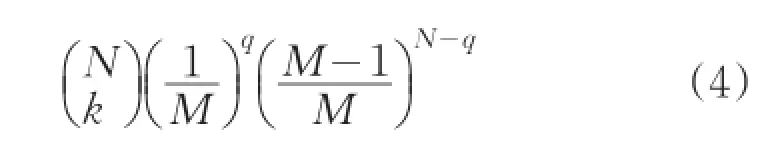
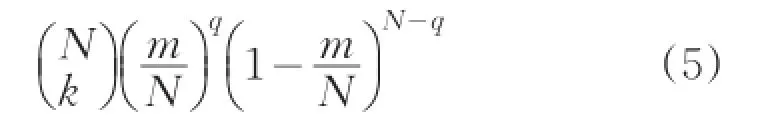
当m较小时，可用泊松分布近似表示，即

说明任意一条链中key的数量小于m的概率趋向于1。

3　实验结果与分析

本文对100万条长度为100的DNA序列进行了测试。实验的硬件平台为2.6GHz的CPU和8G内存，操作系统为64位Windows7，软件平台为Dec-C++Version5.7.1，编译器为TDM-GCC 4.8.1 64-bit Release。

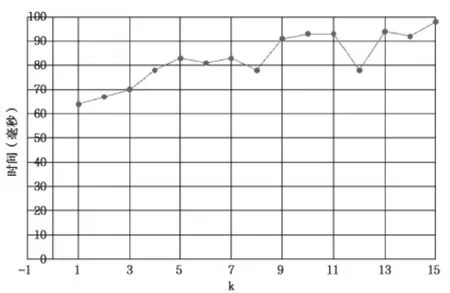
图5　0＜k≤15时查询100万次所需时间

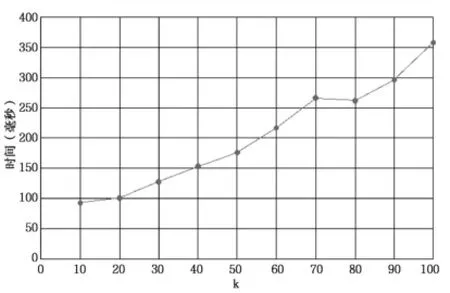
图6　k＞15时查询100万次所需时间

图7　建立索引所需时间

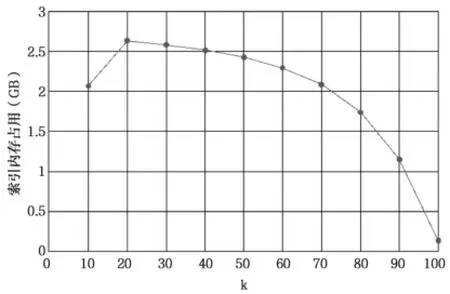
图8　索引占用内存

实验结果如图5（0＜k≤15时查询100万次所需时间）、图6（k＞15时查询100万次所需时间）、图7（建立索引所需时间）、图8（索引占用内存）所示，根据结果分析可知：在0＜k≤15时适用于顺序索引模型的数据结构，k＞15时适用于散列索引模型的数据结构。

4　结论

本文针对不同长度的k-mer分别应用了两种Hash映射关系。从实验结果可以看出，两者相互结合，互为补充，可以有效的解决DNA序列的k-mer索引问题。

［1］ Cormen T H.算法导论（第2版）［M］.北京：机械工业出版社，2006.

［2］ Robert Sedgewick.算法（第4版）［M］.北京：人民邮电出版社，2015.

［3］ 严蔚敏，吴伟民.数据结构［M］.北京：清华大学出版社，2014.

［4］ 成丽波，蔡志丹，周蕊，等.大学数学实验教程（第2版）［M］，北京：北京理工大学出版社，2015.

［5］ 赵国峰，闫亮.用于快速流分类的关键字分解Hash算法［J］.计算机工程，2010，36（16）：79-81.

［6］ 林勇.面向下一代测序技术的de novo序列拼接工具综述［J］.小型微型计算机系统，2013，34（3）：627-631.

［7］ 郑莹，欧阳丹彤，何丽莉，等.基于Hash函数的抵御失去同步RFID安全认证协议［J］.吉林大学学报：理学版，2015，53（3）：499-504.

［8］ 李锦青，柏逢明，底晓强.基于Hopfield混沌神经网络的彩色图像加密算法研究［J］.长春理工大学学报：自然科学版，2012，35（4）：117-121.

［9］ 赵希奇，柏逢明，吕贵花.基于混沌理论和Hash函数的自适应图像加密算法［J］.长春理工大学学报：自然科学版，2014，37（4）：117-120.

The Mathematical Model of k-mer Index for DNA Sequence Problem Based on Hash Algorithm

GUO Fangzhou，HUA Yang，DONG Xiuwei，CAI Zhidan
（School of Science，Changchun University of Science and Technology，Changchun 130022）

In this paper，we give the mode of building and searching index for DNA similar sequences.Based on the Hash algorithm，we establishthe order index model and Hash indexing model which depend on the size of the k value.In orter to avoid Hash-Clash，we chose DJBhash fuction under the larger k value.Finally，we give the time of buliding and searching index and the memory occupation with different k value which CPU is 2.6GHz，memory is 8G，operation system is window 7 at 64 bit，at the same time，we test 1 million of DNAsequencewiththe length of 100，solve the k-mer index problem of DNA sequence effectively.

Hash algorithm；index problem；mathematical model；complexity analysis

O244

A

1672-9870（2015）05-0116-04

2015-07-01

国家自然科学基金（NSFC：11326078）

郭方舟（1993-），男，本科，E-mail：940481517@qq.com

蔡志丹（1979-），女，副教授，E-mail：1261046008@qq.com