基于混沌和多群体的粒子群优化算法

宫玉琳，文大化

（1.长春理工大学　电子信息工程学院，长春　130022；2.中国科学院长春光学精密机械与物理研究所，长春　130033）

基于混沌和多群体的粒子群优化算法

宫玉琳1，文大化2

（1.长春理工大学电子信息工程学院，长春130022；2.中国科学院长春光学精密机械与物理研究所，长春130033）

由于基本粒子群优化算法存在初始化随机性和遍历性不强，全局搜索容易陷入局部最优的问题，提出了基于混沌和多群体的粒子群优化算法，利用混沌特性初始化粒子，增强其随机性和遍历性，并根据适应度值将粒子群划分为多个群体，对不同群体中粒子的速度和位置采取不同的计算方法，进一步提高算法的收敛速度和精度。

混沌；多群体；粒子群优化

粒子群优化（Particle Swarm Optimization，PSO）算法［1］，通过追随当前搜索到的最优值来寻找全局最优，在求解优化问题等方面已经得到了越来越广泛的应用。

1　基本粒子群优化算法

PSO算法模拟鸟群寻找食物的过程，在寻找食物的过程中，鸟不停地改变自己在空间飞行的位置和速度，每只鸟都可以用一个粒子来表示，粒子的参数也就是需要求解问题的可能解。假设m个粒子组成的粒子群在D维空间中进行搜索，其中，第i个粒子在D维空间中的位置表示为xi=（xi1，xi2，…，xiD），第i个粒子所经历过的最优位置表示为Pi=（pi1，p12，…，piD），每个粒子的飞行速度表示为Vi=（vi1，v12，…，viD），所有粒子经历过的最优位置表示为Pg=（pg1，pg2，…，pgD），例如：pg1表示第一个粒子经历过的最优位置。粒子群中单个粒子的迭代过程如图1所示。

图1　粒子迭代过程

在搜索的过程中，每个粒子各自的速度和位置分别通过公式（1）和（2）进行更新：式中，i表示第i个粒子；d表示粒子的第d维；k表示迭代次数；w为惯性因子；c1和c2为学习因子；r1和r2为［ ］0，1区间的随机数。

2　混沌初始优化

为了增强粒子初始的遍历性和随机性，通过公式（3）的Logistic映射［2，3］对粒子分布进行优化：

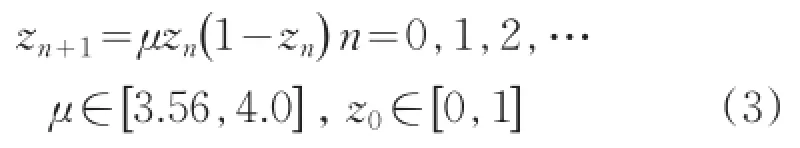
式中，μ为控制参量，决定了混沌系统的混沌状态程度。

混沌初始化的过程包括如下步骤：

（1）随机生成一个向量z0=［z01，z02，…，z0n］，n为粒子的维数；

（3）将混沌向量映射到定义域X上，第i个粒子可以表示为：

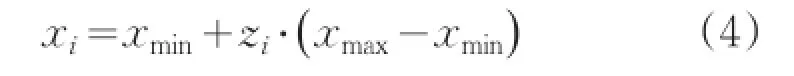
式中，xmax和xmin分别为粒子取值的上下限。

3　多群体优化

3.1早熟收敛程度评价

由PSO算法的原理可知，粒子在搜索全局最优解的过程中，趋同性会越来越强，这将使得粒子的多样性受到极大限制。为了减弱趋同性又会使粒子的多样性受到影响，这将减小算法的收敛速度。因此，选择合适的早熟收敛评价指标十分重要，为了合理的评价粒子群的早熟收敛程度，本文采用公式（5）和式（6）对其进行评价：

式中，N表示粒子总数；fi表示第i个粒子的适应度值；favg表示N个粒子的平均适应度值；fg表示粒子的最优适应度值；表示所有优于 favg的适应度值的平均值；Δ即为早熟评价指标，Δ值越大表明粒子群早熟程度越低。

3.2多群体划分

本文根据早熟收敛评价指标，将整个粒子群划分为最优群体、一般群体和最差群体三个子群体［4，5］，如图2所示。

图2　多群体划分

划分的群体采用非均匀划分的方式，最优群体和最差群体各占整个群体的25%，一般群体占整个群体的50%。由于最优群体中粒子的适应度值较高，所以该群体中的粒子更接近全局最优解。但是，这些粒子受群体最优影响严重，弱化了粒子个体最优的作用。粒子通过式（7）调整速度，同时根据式（8）调整粒子的惯性因子w：

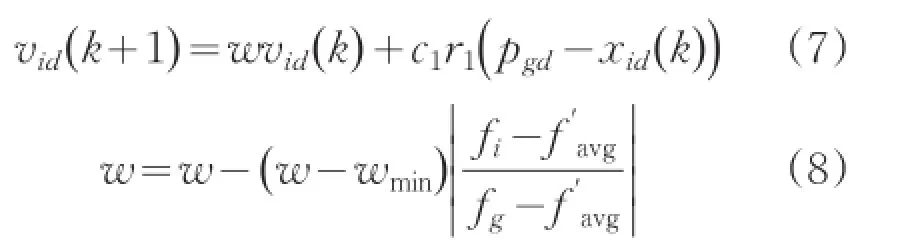
式中，wmin为惯性因子w的最小值。由式（8）可以看出，适应度值越好的粒子对应的惯性因子越小。通过采用种策略，使得算法接近收敛时具有更强的局部搜索能力。

（1）自然环境状况。洞庭湖东、南、西三面为山脉高地，北部为平原水网地区。湖区四季分明，降水充沛，生物资源丰富，有水生高等植物311种，浮游动物90种，底栖动物67种，鱼类113种，鸟类216种，水生哺乳类动物22种，其中有中华鲟、白鲟等国家一级、二级保护动物48种，国家一、二级保护植物30多种，是国家重点保护野生动物江豚和麋鹿的栖憩地。

一般群体中的粒子在全局寻优能力和局部寻优能力方面都有较好的能力。因此，速度更新可直接采用式（1）进行，惯性因子w则通过式（9）进行调整：

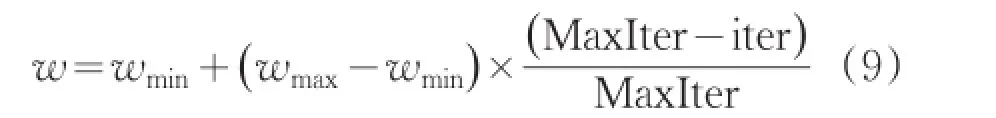
惯性因子随着搜索的进行逐渐减小，使得搜索开始时具有较高的搜索效率，并且在搜索后期具有提高搜索精度。

最差群体中的粒子搜索能力较差，需要借助一般子群体中的位置信息，因此采用式（10）对速度进行更新，惯性因子w通过式（11）进行调整：

当粒子松散地分布于搜索空间时，根据式（6）可以算得此时的Δ值较大，这时将Δ代入式（11）可得较小的w，使得算法具有较强的局部搜索能力，能够加强粒子的收敛；当粒子集中分布于搜索空间时，则根据式（6）算得的Δ值较小，此时由式（11）可得较大的w，使得算法具有较强的全局搜索能力，能够使粒子跳出局部最优。

对于式（11），可以看到参数k1和k2的选择对w的取值有着很重要的影响。其中，k1主要用来决定w的最大值，k1取值越大，则w的最大值越大。根据上文的分析可知，w的取值应大于1。因此，k1需取大于1的常数，这样才能使式（11）计算得到的w大于1。在本文算法中，取k1=1.5，通过可以计算可以得到w的取值范围：0.5＜w＜1.1。k2主要用来决定惯性因子w的调节，k2的取值越大，在早期停滞时，w的调节能力越强，使得算法具有较快的收敛速度，但是会使算法的收敛精度受到影响；k2的取值越小，惯性因子w的调节能力越弱，当粒子集中地分布于搜索空间时，算法不能有效地跳出局部最优。

4　算法测试与仿真分析

为了对本文算法的性能进行分析，选用了三个典型的测试函数：Rosenbrock函数、Griewank函数以及Rastrigin函数，对算法性能进行了仿真分析。

（1）Rosenbrock函数的局部最优值和全局最优值十分接近，全局最优值的求解比较复杂。Rosenbrock函数的表达式如公式（12）所示，维度为3的Rosenbrock函数如图3所示。

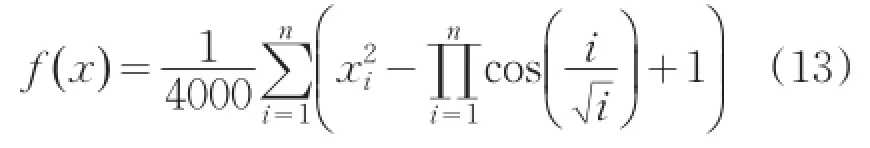
（3）Rastrigin函数也是一个多峰值函数，存在很多局部最优解，对于求解全局最优解也是十分复杂的。Rastrigin函数的表达式如公式（14）所示，维度为3的Rastrigin函数如图5所示。

典型测试函数的参数如表1所示。

表1　典型测试函数的参数

为了对比算法的效果，本文将CMPSO算法分别与PSO算法与遗传算法（GA）进行对比分析。测试过程中，每种算法迭代500次，各算法的参数如表2所示。

表2　各算法参数

当测试函数的维度n=10时，得到五种测试函数的测试曲线如图6至图8所示。采用三种算法对测试函数得到的平均最优值和最优值如表3所示。由图6至图8和表3可见，典型的测试函数，粒子群优化算法的速度明显快于遗传算法的优化速度，并且收敛精度高。其中，对于Rastrigin函数，尽管开始时基本粒子群优化算法的收敛速度最快，但随着迭代次数的增加，收敛速度逐渐变慢，最终的收敛精度也明显不及改进的粒子群优化算法。

图3　维度n=3时的Rosenbrock函数

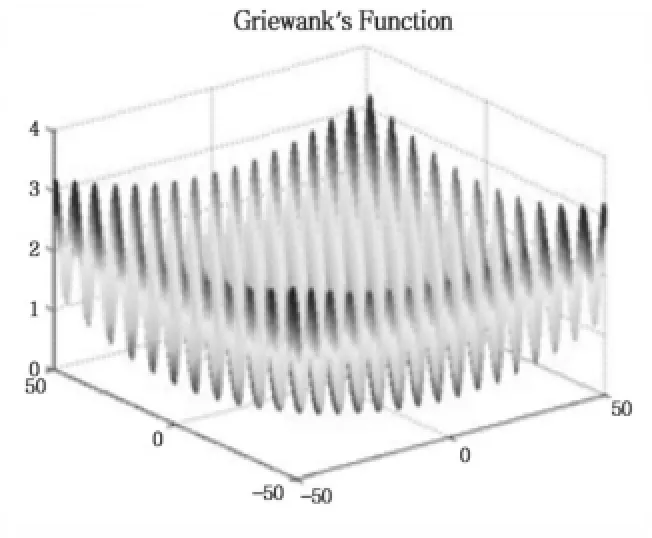
图4　维度n=3时的Griewank函数

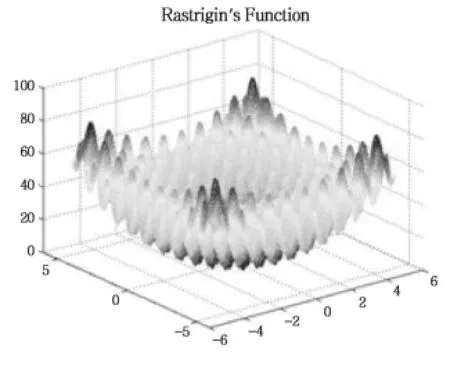
图5　维度n=3的Rastrigin函数

图6　Rosenbrock函数平均适应值曲线

图7　Griewank函数平均适应值曲线

图8　Rastrigin函数平均适应值曲线

表3　三种算法得到的平均最优值和最优值

5　结论

本文采用Logistic映射对粒子进行混沌初始化，使粒子在初始时具有较好的遍历性，增强了粒子的全局搜索能力。同时，根据早熟收敛评价指标将整个粒子群划分为多个群体，针对不同群体采取与之适应的计算方法，解决了基本粒子群体算法易陷入局部最优、早熟收敛的问题，尽管运算量有所增加，但仿真结果表明，本文算法具有收敛速度较快、收敛精度高的特点，明显优于遗传算法和基本粒子群优化算法。

［1］ Kennedy J，Eberhart R.Swarm Intelligence［M］.San Francisco：Morgan Kaufman Publishers，2001.

［2］Wang T Y，Huang C Y.Applying optimized BPN to a chaotic time series problem［J］.Expert Sys-tems with Applications，2007，32：193-200.

［3］Poli R，Langdon W B，Clerc M，et al.Continuous optimization theory made easy Finite-element models of evolutionary strategies，genetic algorithms and particle swarm optimizers［M］.LNCS，Proceedings of thefoundationsofgeneticalgorithmsworkshop，Springer，Berlin，2007.

［4］ Huynh D C，Dunnigan M W.Parameter estimation ofaninductionmachineusingadvancedparticle swarm optimization algorithms［J］.IET Electric Power Applications，2010，4（9）：748-760.

［5］Blackwell T，Branke J.Multiswarms，exclusion，and anti-convergence in dynamic environments［J］.IEEE Transactions on Evolutionary Computation，2010，10 （4）：459-472.

［6］Huang Fang，Fan Xiaoping.Parallel particle swarm optimization algorithm based on island group model ［J］.Control and Decision，2006，21（2）：75-188.

［7］Huang T，Mohan A S.A hybrid boundary conditionforrobustparticleswarmoptimization［J］. IEEE Antennas and Wireless Propagation Letters，2012（4）：112-117.

［8］ Xu S，Rahmat Samii Y.Boundary conditions in particle swarm optimization revisited［J］.IEEE AntennasandWirelessPropagationLetters，2011，55（3）：760-765.

Particle Swarm Optimization Algorithm Based on Chaos and Multi Group

GONG Yulin1，WEN Dahua2
（1.School of Electronic and Information Engineering，Changchun University of Science and Technology，Changchun 130022；2.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Science，Changchun 130033）

Because the basic particle swarm optimization algorithm has the problem that the initialization of the algorithm is easy to fall into local optimum，the global search is easy to fall into local optimization.The particle swarm optimization algorithm based on chaos and multi population is proposed.The algorithm can be used to improve the speed and accuracy of different populations.

chaos；multi group；particle swarm optimization

TP301

A

1672-9870（2015）05-0088-04

2015-09-16

宫玉琳（1983），男，博士，讲师，E-mail：garrygong1983@126.com