岩溶区分岔隧道底板的安全厚度

周栋梁，邹金锋



岩溶区分岔隧道底板的安全厚度

周栋梁1，邹金锋2

(1. 湖南省高速公路管理局，湖南长沙，410001；2. 中南大学土木工程学院，湖南长沙，410075)

基于岩石剪切、冲切破坏的Mohr判据和格里菲斯判据，考虑溶洞平面投影边缘处的弯拉破坏和剪切破坏、中隔墙底部岩层的冲切破坏和剪切破坏破坏模式，分别建立这4种破坏模式下岩溶区分岔隧道底板安全厚度预测公式。采用湖南湘西某高速公路岩溶区分岔隧道岩体的物理力学参数、溶洞半径与形状和隧道埋深等9个因素，分析它们对分岔隧道底板安全厚度的敏感性和影响规律。研究结果表明：由所建立的预测公式所得结果与数值计算结果一致，且底板安全厚度预测公式简单，便于工程实用；底板安全厚度的主要影响因素为岩石黏膜聚力、溶洞跨度、岩石内摩擦角和隧道埋深。

岩溶；分岔隧道；底板安全厚度；预测模型

分岔隧道是一种新颖的隧道结构形式，它一般由四车道大拱隧道或连拱隧道逐渐过渡到上下行分离式双洞隧道，因此，它同时具有标准间距的分离隧道、小净距隧道、连拱隧道以及四车道大拱隧道等多种结构形式隧道的特点。随着我国西部大开发战略的逐步实施，在高山峡谷等岩溶地质灾害常见地段修建分岔隧道结构在所难免。在隧道穿越较大规模岩溶区的施工过程中，主要面临位于隧道和溶洞间岩层的稳定性问题[1−4]。由于岩层失稳发生的时间和空间很难预测，且目前国内对分岔隧道尚无相应的设计、施工技术规范和标准可循，研究岩溶区隧道与周围隐伏溶洞间的安全厚度，确保两者间岩层的稳定性对保证岩溶区隧道施工及运营期的安全具有重要的现实意义，是当前岩溶区隧道建设中亟待解决的课题。目前，针对存在较大尺度隐伏溶洞的隧道底板所需安全厚度的研 究[5−7]中，多是将隐伏溶洞与隧道间的岩层简化为弹性梁和板的力学模型，基于岩体抗拉(剪)强度准则或突变理论建立岩层最小安全厚度分析模型，但尚无针对岩溶区分岔隧道底板安全厚度的相关研究。为此，本文作者结合我国西部山区分岔隧道建设实践，充分考虑分岔隧道可能出现的破坏模式，对存在较大尺度下伏溶洞的分岔隧道底板所需安全厚度进行研究，采用理论分析和数值计算等手段，以期提出一套经济合理、安全可靠且便于工程应用的分岔隧道底板安全厚度的预测方法。

1 岩溶区分岔隧道过渡段底板安全厚度预测公式

1.1 溶洞水平面投影边缘处的破坏形式

1.1.1 弯拉破坏

若隧道底板发生弯拉破坏，则将隧道和溶洞间岩层简化为两端固定梁，如图1所示。

图1 底板岩层受力简化示意图

岩柱梁最大拉应力在固定端端部，需满足经典的岩体强度理论中的最大正应力理论：

1.1.2 剪切破坏

若隧道底板在溶洞边缘处发生剪切破坏，假定岩层所受的平均剪应力为，考虑隧道底板自重和隧道中墙荷载，则由平衡条件可得

采用岩石剪切破坏的莫尔判据，可得分岔隧道底板边缘处溶洞段的底板安全厚度预测公式。

1) 当岩性较坚硬至较软弱时，

2) 当岩性坚硬至较坚硬时，

由式(3)，(5)和(6)可知安全厚度与隧道中墙荷载正相关。在分岔隧道连拱段，＞0，在大拱段可以认为=0，则上述2种破坏模式首先应该发生在连拱段。对于分岔隧道中墙下的荷载，由文献[8]中墙承载模型，可得每延米中墙下的荷载为

1.2 隧道底板中墙下方处的破坏形式

1.2.1 冲切破坏

若中墙底部持力岩层发生冲切破坏，如图2所示，则会形成1个截面为梯形的冲切体[9−12]，冲切角为。

图2 分岔隧道底板冲切破坏模式

将图2中的计算模型简化成二维问题，如图3所示。图3中：分岔隧道中墙宽度为，中墙下隧道底板厚度为1，在每延米中墙底部垂直荷载为1。假定冲切面上的应力均匀分布，且不考虑顶板下填充物的顶托力，则由静力平衡条件可得冲切面上的平均应力为

用平面应力状态公式将冲切面上的应力转化为主应力状态表达式，得

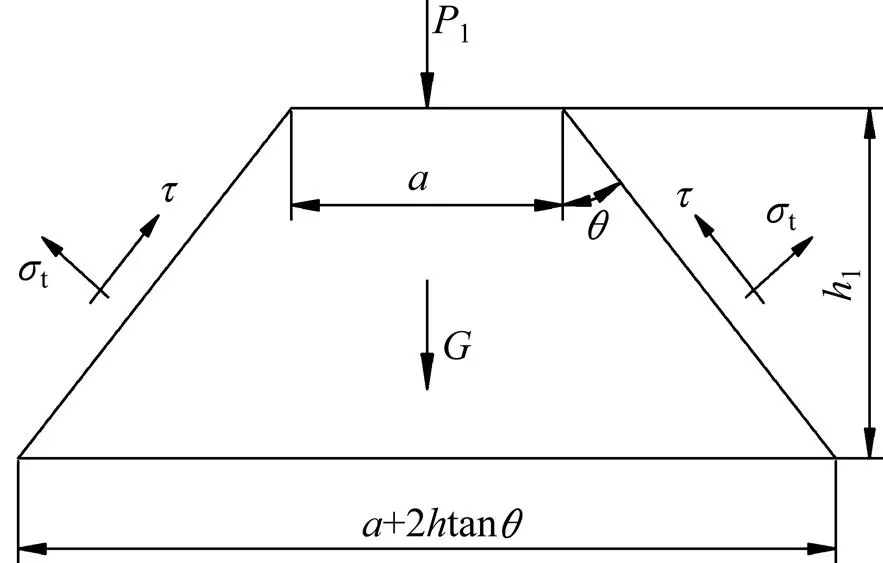
图3 冲切破坏示意图

采用格里菲斯强度判据可求得

1.2.2剪切破坏

若中墙底部持力岩层发生剪切破坏，如图4所示，此时中墙底部均布荷载为2，剪切应力为。不考虑剪切体的自重和顶板下充填物的顶托作用，并假定剪切面上应力均匀分布，则由平衡条件可以求得剪切面上的剪应力为

图4 中墙底部岩层的剪切破坏示意图

采用岩石的剪切破坏用莫尔判据，当岩性较坚 硬—较软弱时，

在岩性坚硬、较坚硬时，

2 理论与数值计算结果对比分析

由于有限元对非匀质、非线性和复杂边界条件的问题求解十分方便[13−15]，因而，研究分岔隧道过渡段与下方隐伏溶洞间岩层最小安全厚度时，采用有限元数值计算是一种比较方便可靠的方法。为此，为验证理论预测模型的有效性，本文采用数值模拟的手段进行对比分析和验证。数值计算的模型根据图5所反映的工程实例建立。

图5 模拟范围

2.1 工程概况与计算参数

湘西某隧道拟采用分岔隧道的形式，围岩岩溶发育，隧道埋深80.0 m左右，中墙厚1.5 m，一侧隧洞中线至中墙的距离为4.9 m。根据地质勘探报告，岩块单轴抗压强度c=100 MPa，取岩石抗拉强度，弹性模量=8 GPa，泊松比，内摩擦角40°，黏聚力=0.9 MPa，岩体平均容重取24 kN/m3。

2.2 下伏溶洞分岔隧道施工过程三维数值计算

数值分析计算范围如下：在大拱隧道与小近距隧道分界面处沿隧道走向向两边各取10 m，总长20 m；模型水平方向长度取6~10倍隧道洞跨，为160 m；模型底部距隧道地板深度取80 m；隧道埋深取到地面高度，为80 m。溶洞位于分岔隧道正下方，采用受力较差的椭圆形状，溶洞跨度取6 m，高度取3 m；围岩材料的力学屈服准则采用岩土工程中常用的摩尔−库仑模型，中墙及支护结构均看作弹性材料。计算模型网格划分示意图如图6所示。

图6 计算模型网格划分示意图

经反复调整模型中的溶洞与隧道之间的距离，得到分岔隧道过渡段底板的安全厚度临界值为4.6 m。塑性区分布云图如图7和图8所示。中隔墙底部围岩塑性区恰好贯通，连拱段左右洞边墙墙脚也产生了塑性区，但其未发展到与溶洞贯通。

图7 分岔隧道开挖结束后塑性区分布云图

图8 分岔隧道开挖结束后塑性区分布云图(剖面)

2.3 理论计算与数值计算的对比

采用式(3)，(6)，(12)和(15)进行理论预测，得到溶洞平面投影边缘处发生弯拉破坏时的隧道底板安全厚度为3.40 m，溶洞平面投影边缘处发生剪切破坏时的隧道底板安全厚度为0.35 m、中墙下方处发生冲切破坏时的隧道底板安全厚度为5.10 m，中墙下方处发生剪切破坏时的隧道底板安全厚度为0.32 m。取计算结果最大值，可得底板安全厚度的理论预测值为5.10 m，与数值模拟的结果(4.60 m)相差不大，相对误差为9.80%。中隔墙下方最易发生冲切破坏。从二者的对比分析结果可以看出，理论计算结果偏于保守。

3 分岔隧道与下伏溶洞间最小安全厚度影响因素敏感性分析

为了进一步研究分岔隧道与其下方隐伏溶洞间岩层的最小安全厚度的主要影响因素，在上述数值计算模型的基础上考虑多种可能的影响因素，设计正交试验，采用ABAQUS软件对分岔隧道与下伏溶洞间最小安全厚度影响因素敏感性进行模拟分析。

3.1 影响因素和试验方案

影响分岔隧道与下伏溶洞间最小安全厚度的影响因素主要包括[16−17]：岩体的物理力学特性如黏聚力、内摩擦角、泊松比、容重、弹性模量；溶洞半径与形状如溶洞跨度、溶洞高跨比；隧道埋深和地表倾斜坡角。根据工程实际勘测资料中统计出的Ⅲ和Ⅳ级围岩参数分布范围，将上述9个影响因素分别设定为4个水平，如表1所示，选用32(49)正交表进行正交试验。

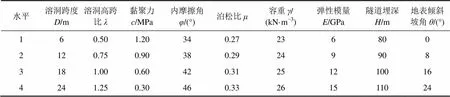
表1 影响因素与水平

3.2 正交试验结果分析

正交试验结果见表2，安全厚度均值为4.90 m。表3所示为通过对正交试验结果的进行直观分析所得的各影响因素极差。为了分析影响实验结果各因素的重要程度，对试验结果进行方差分析，见表4。

表2 正交试验结果

表3 极差分析结果

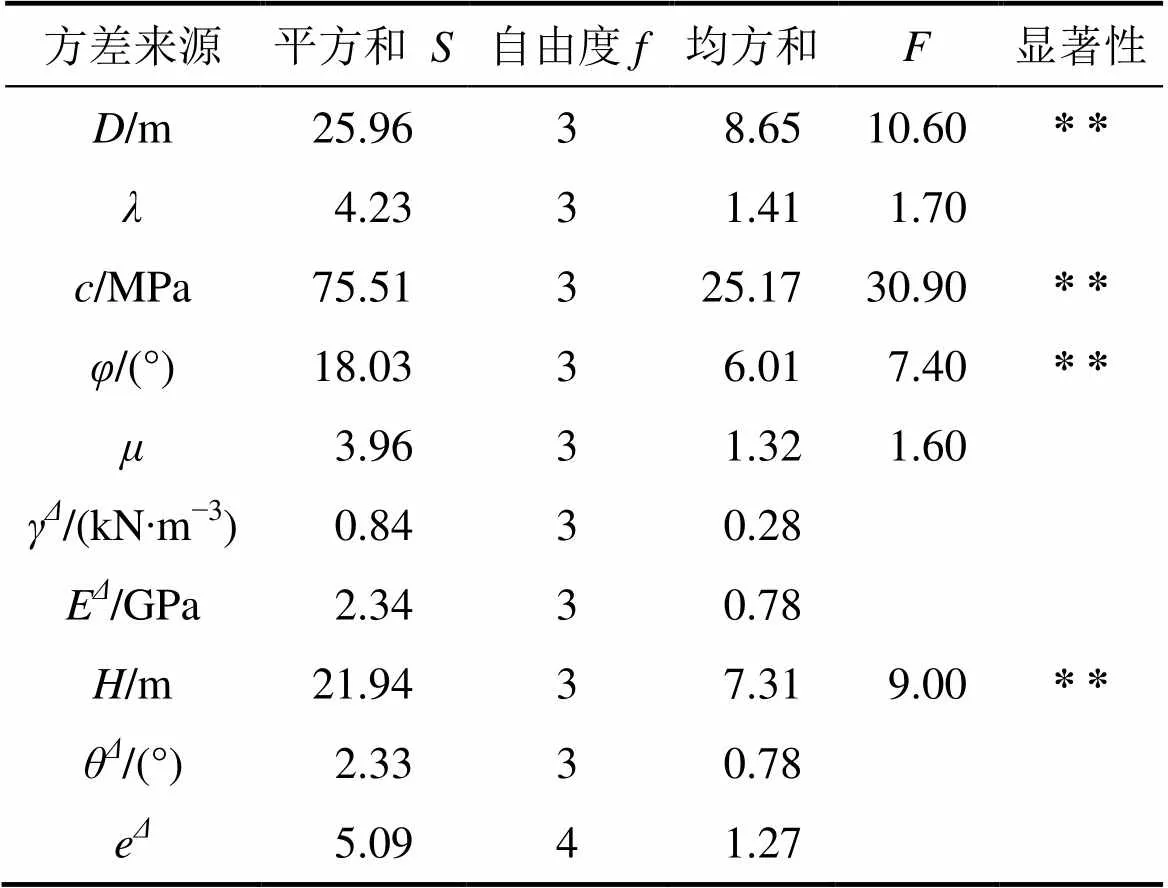
表4 方差分析结果

注：0.01(3,13)=5.74；0.1(3,13)=2.56；γ表示方差为的容重；E表示方差为的弹性模量；θ表示方差为的内摩擦角；e表示方差为的误差。

根据各因素极差的大小顺序，可以确定影响因素由主到次的顺序为：，，，，，，，和。从表3可以看出：岩石黏聚力、溶洞跨度、岩石内摩擦角和隧道埋深对分岔隧道与下伏溶洞间岩层最小安全厚度影响十分显著，溶洞高跨比、岩石泊松比则无显著影响，而影响更小的地表斜坡坡角、围岩弹性模量和围岩容重则几乎无影响。由于本文采用的溶洞半径较大，当溶洞跨度较大时，会减小隧道结构的应力集中度，隧道周围塑性区减小，从而造成顶板所需安全厚度减小；岩体材料模型采用摩尔—库仑弹塑性模型，黏聚力和内摩擦角直接反映了岩体的抗剪强度，所以，两者的变化会对塑性区的分布产生很大影响；分岔隧道底板安全厚度随隧道埋深的增加而增加，而岩体容重和地表斜坡坡角对分岔隧道底板安全厚度几乎没有影响；泊松比变化对分岔隧道底板安全厚度的影响不显著，岩体弹性模量对分岔隧道底板安全厚度的影响很小，这是因为弹性模量对变形量影响较大，而对塑性区的分布无太大影响。

4 结论

1) 考虑了溶洞平面投影边缘处的弯拉破坏和剪切破坏以及中隔墙底部岩层冲切破坏和剪切破坏共4种破坏模式，推导出一套预测分岔隧道底板岩层安全厚度的计算公式。

2) 岩石黏聚力、溶洞跨度、岩石内摩擦角和隧道埋深对分岔隧道与下伏溶洞间岩层最小安全厚度影响十分显著。

3) 综合分析和讨论了岩溶地区分岔隧道底板厚度的安全影响因素，给出了评价方法和指标，可供岩溶地区工程设计和施工参考。

[1] 康勇, 杨春和, 张朋. 浅埋岩溶隧道灾变机制及其防治[J]. 岩石力学与工程学报, 2010, 29(1): 149−154.KANG Yong, YANG Chunhe, ZHANG Peng. Disaster-induced mechanism and its treatment in shallow-buried karst tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 149−154.

[2] 吴梦军, 许锡宾, 赵明婕, 等. 岩溶地区公路隧道施工力学响应研究[J]. 岩石力学与工程学报, 2004, 23(9): 1525−1529.WU Mengjun, XU Xibin, ZHAO Mingjie, et al. Construction mechanics response study of highway tunnel in karst[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(9): 1525−1529.

[3] 王勇, 乔春生, 孙彩红, 等. 基于SVM的溶洞顶板安全厚度智能预测模型[J]. 岩土力学, 2006, 27(6): 1000−1004.WANG Yong, QIAO Chunsheng, SUN Caihong, et al. Forecasting model of safe thickness for roof of karst cave tunnel based on support vector machines[J]. Rock and Soil Mechanics, 2006, 27(6): 1000−1004.

[4] 雷明锋, 彭立敏, 施成华, 等. 岩溶段连拱隧道列车振动响应及地基累积变形[J]. 中南大学学报(自然科学版), 2014, 45(3): 826−832. LEI Mingfeng, PENG Limin, SHI Chenghua, et al. Train vibration response and cumulative deformation of double arch tunnel in krast foundation[J]. Journal of Central South University (Science and Technology), 2014, 45(3): 826−832.

[5] 林杭, 曹平, 李江腾, 等. 采空区临界安全顶板预测的厚度折减法[J]. 煤炭学报, 2009, 34(l): 53−57.LIN Hang, CAO Ping, LI Jiangteng, et al. The thickness reduction method in forecasting the critical safety roof thickness of gob area[J]. Journal of China Coal Society, 2009, 34(l): 53−57.

[6] 王丽霞, 凌贤长,张云龙. 哈尔滨市松花江隧道顶部覆土安全厚度预测模型[J]. 岩石力学与工程学报, 2003, 22(5): 849−854. WANG Lixia, LING Xianchang, ZHANG Yunlong. Forecasting model of safe cover thickness of tunnel crossing Songhua River in Harbin[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5): 849−854.

[7] 黎斌, 范秋雁, 秦凤荣. 岩溶地区溶洞顶板稳定性分析[J]. 岩石力学与工程学报, 2002, 21(4): 532−536. LI Bin, FAN Qiuyan, QIN Fengrong. Analysis on roof stability of karst cave in karst areas[J]. Chinese Journal of Rock Mechanic and Engineering, 2002, 21(4): 532−536.

[8] 李术才, 王汉鹏, 郑学芬. 分岔隧道稳定性分析及施工优化研究[J]. 岩石力学与工程学报, 2008, 27(3): 447−457. LI Shucai, WANG Hanpeng, ZHENG Xuefen.Forked tunnel stability analysis and its construction optimization research[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 447−457.

[9] 赵明华, 陈昌富, 曹文贵, 等. 嵌岩桩桩端岩层抗冲切安全厚度研究[J]. 湘潭矿业学院学报, 2003, 18(4): 41−45.ZHAO Minghua, CHEN Changfu, CAO Wengui, et al. Analysis for the safe terrain thickness of punching-shear resistance at the end of rock−socked piles[J]. Journal of Xiangtan Mining Institute, 2003, 18(4): 41−45.

[10] 赵明华, 曹文贵, 何鹏祥, 等. 岩溶及采空区桥梁桩基桩端岩层安全厚度研究[J]. 岩土力学, 2004, 25(1): 64−68. ZHAO Minghua, CAO Wengui, HE Pengxiang, et al. Study on safe thickness of rock mass at end of bridge foundation’s pile in karst and worked-out mine area[J]. Rock and Soil Mechanics, 2004, 25(1): 64−68.

[11] 符策简. 岩溶地区隐伏溶洞顶板稳定性及变形分析[J]. 岩土力学, 2010, 31(增2): 288−292. FU Cejian. Analysis on roof stability and deformation of concealed cave in karst regions[J]. Rock and Soil Mechanics, 2010, 31(Suppl 2): 288−292.

[12] 刘晓明, 何青相, 赵明华. 岩溶地基上桥梁桩基设计优化方法研究与实例[J]. 中南大学学报(自然科学版), 2014, 45(5): 1653−1658. LIU Xiaoming, HE Qingxiang, ZHAO Minghua. Optimization design of bridge pile foundation in karst region: Methodology and examples[J]. Journal of Central South University (Science and Technology), 2014, 45(5): 1653−1658.

[13] 赵明阶, 刘绪华. 隧道顶部溶洞对围岩稳定性影响的数值分析[J]. 岩土力学, 2003, 24(3): 445−449. ZHAO Mingjie, LIU Xuhua. Numerical analysis of influence of karst caves in top of tunnel on stability of surrounding rock masses[J]. Rock and Soil Mechanics, 2003, 24(3): 445−449.

[14] 赵明阶, 敖建华, 刘绪华, 等. 隧道底部溶洞对围岩变形特性的影响分析[J]. 重庆交通学院学报, 2003, 22(2): 20−23. ZHAO Mingjie, AO Jianhua, LIU Xuhua, et al. Study on deformation character of the surrounding rock masses Concerning the influence of karst caves in the bottom of tunnel[J]. Journal of Chongqing Jiaotong University, 2003, 22(2): 20−23.

[15] 王明华, 杨良策. 大型地下洞室顶板稳定性的岩体结构控制效应[J]. 岩土力学, 2003, 24(3): 484−487. WANG Minghua, YANG Liangce. Control effect of rock mass structure on stability of top slab for large underground cavern[J]. Rock and Soil Mechanics, 2003, 24(3): 484−487.

[16] 曹茜. 岩溶隧道与溶洞的安全距离研究[D]. 北京: 北京交通大学土木建筑工程学院, 2010: 9−56. CAO Qian. Study on safe thickness for rock between tunnel and karst cave in karst region[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2010: 9−56.

[17] JIANG Chong, LIU Lang, WU Junping. A new method determining safe thickness of karst cave roof under pile tip[J]. Journal of Central South University, 2014, 21(3): 1190−1196.

Safe thickness of floor of forked tunnel in karst areas

ZHOU Dongliang1, ZOU Jinfeng2

(1. Hunan Provincial Expressway Administration Bureau, Changsha 410001, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

Based on the Mohr criterion and Griffith criterion in rock shearing failure and punch-shearing failure, the prediction formulas for calculating the safe thickness of the floor of forked tunnel in karst areas were proposed according to four kinds of failure modes respectively, i.e. the terrane bending failure and shearing failure around the planar projection edge of cave, and the terrane punch-shearing failure and shearing failure under the middle wall. Nine factors were considered in analyzing the sensitivities for the safe thickness of the floor of forked tunnel and concluding the influence rules by numerical simulation. Those factors contained the mechanics parameters of rock mass, the size and shape of cave and the tunnel depth of a forked tunnel in karst areas in an expressway in Hunan Province. The results show that the prediction results obtained by the prediction formulas agree well with the numerical results, and the prediction formulas for calculating the safety floor thickness are simple and convenient in application of engineering. The most sensitive factors to the safety floor thickness are the rock cohesion, the width of karst cave, the angle of internal friction and the depth of tunnel.

karst; forked tunnel; safety floor thickness; forecast model

10.11817/j.issn.1672-7207.2015.05.042

TU457

A

1672−7207(2015)05−1886−07

2014−06−10；

2014−08−22

国家自然科学基金资助项目(51208523)；湖南省交通厅科技项目(201121) (Project(51208523) supported by the National Natural Science Foundation of China; Project(201121) supported by Transportation Science and Technology of Hunan Province)

周栋梁，高级工程师，从事交通土工程的建设与管理等研究；E-mail: 2867075362@qq.com

(编辑 陈灿华)