大地电磁人工神经网络反演

王鹤，蒋欢，王亮，席振铢，张道军



大地电磁人工神经网络反演

王鹤1, 2，蒋欢1, 2，王亮3，席振铢1, 2，张道军3

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 中南大学海洋矿产探测技术与装备研究所，湖南长沙，410083；3．长沙五维地科勘察技术有限责任公司，湖南长沙，410205)

为提高大地电磁非线性反演的计算效率和精度，将人工神经网络引入大地电磁数据反演。神经网络输入为已知地电模型的视电阻率数组，输出为地电模型参数。采用BP算法(back propagation algorithm)进行学习训练，通过信息正向传播和误差反向传播，迭代计算得出神经网络连接权值的最优值；再将训练好的神经网络对未知模型的视电阻率进行反演。对2层和3层大地电磁模型分别建立神经网络并测试反演，研究结果表明：该反演方法能实时准确地逼近真实模型，验证了该方法的可行性和有效性。

大地电磁；神经网络；反演

自大地电磁测深法被提出以来，其反演问题一直是地球物理工作者研究的重点。Robertl[1]对大地电磁一维反演方法进行了系统归纳和总结，随后，OCCAM反演[2]、简化基OCCAM反演[3]、快速松弛反演[4]和非线性共轭梯度反演[5]逐渐应用于电磁法反演，开创了非线性反演的先河。陈小斌等[6]提出了最平缓模型约束下的大地电磁一维连续介质的自适应正则化反演算法；徐义贤等[7]利用小波变换理论中的多尺度分析方法，克服了传统广义逆反演方法易陷入局部极小的弊端；谭捍东等[8]获得了三维快速松弛反演算法的灵敏度函数表达式，实现了求最小构造的三维快速松弛反演算法；严良俊等[9]将二次函数逼近非线性优化应用于大地电磁测深反演问题，实现了对目标函数的全局极小寻优。由于非线性反演方法在原理上各有特色，也各有不足，目前某一种方法不能绝对优于其他方法。在地球物理工作者致力于改善各种方法不足的同时，各种新的理论和方法也不断涌现，如神经网络、遗传算法等完全非线性反演方法具有无需计算雅克比矩阵和全局寻优等特点[10]。在神经网络反演的应用上，国外学者主要在电阻率反演[11]和大地电磁反演[12]上开展了研究。在国内，杨立强等[13]进行了神经网络对地震剖面的波阻抗参数反演，贺懿等[14]采用神经网络对面波的频散曲线进行拟合迭代，反演预测滩浅海低降速带地层参数，说明神经网络在地球物理非线性反演中具有广阔的应用前景。本文论述神经网络的基本原理，并将神经网络引入于大地电磁数据反演中，对2层和3层模型分别进行网络训练和反演实验，并用3层模型网络对实测视电阻率进行反演，以便为提高大地电磁反演速度和工作效率进行研究。

1 人工神经网络方法原理

人工神经网络(artificial neural network, ANN)也称作神经网络(neural network, NN)，是由大量神经元(也叫节点)广泛互连而成的网络。神经网络分为学习(即训练)过程和测试(即反演)过程2部分，先对已知数据进行网络学习训练，再将训练好的网络对未知数据进行测试反演。神经网络的核心算法在于其学习过程。基于神经网络的大地电磁反演希望通过输入已知理论模型的视电阻率数组，采用一系列学习过程得到网络连接权值的最优值，使网络实际输出与理论输出(即理论模型参数数组)的误差达到所需精度。这种学习方式属于有导师的学习，而前向型神经网络是一种基于导师学习的神经网络，能够通过学习已知通用数据而掌握经验，从而对未知数据进行识别。

1.1 前向型神经网络

1个接受个输入的个神经元构成的基本前向型网络结构见图1。

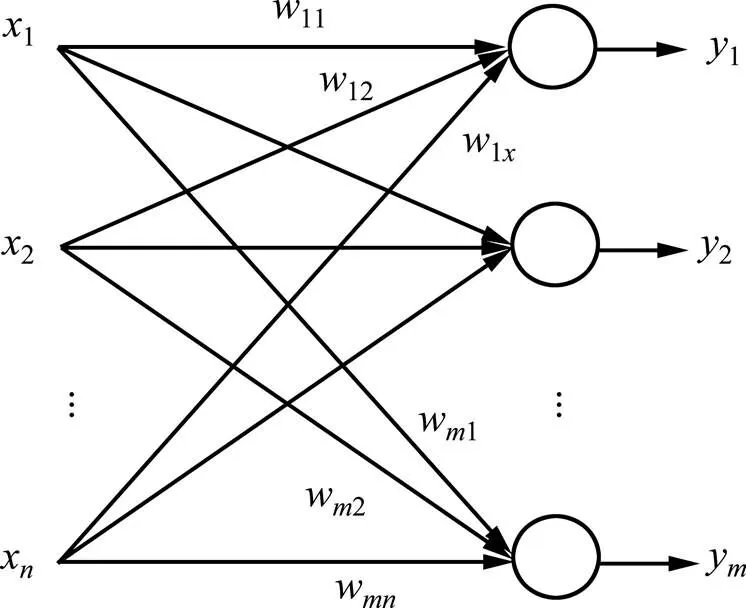
图1 前向型神经网络结构示意图

它的输入和输出分别为：

连接权值w将第个神经元和第个输入连接起来。权值的2个下标和分别表示目标节点和源节点，T表示转置。第个神经元的激活值可写成

包含激活函数(eti) (=1, 2, …,)的非线性变换完成对进行处理，对网络中个神经元进行逐个变换得

其中权向量包含影响第个输出节点的所有权值，

由网络实现的输入空间映射到输出空间可表达为

其中：为权矩阵，也称连接矩阵，

通过某种学习算法计算，可以得到输入空间与输出空间的映射关系，此映射关系为非线性关系，与大地电磁非线性反演的需求相吻合。前向型神经网络的学习算法通常采用反向传播算法(back propagation algorithm，简称BP算法)，故该网络也称为BP神经网络。

1.2 BP神经网络

BP神经网络是最常用的一种神经网络。从结构上来讲，它是一种分层型网络，具有输入层、中间层(也称作隐层)和输出层。

对于1个BP网络，当给定1个输入模式时，输入信号由输入层到输出层的传递是一个前向传播的过程，若输出信号与期望信号有差别即存在误差，则转入误差反向传播的过程，并根据各层误差来调节各层权值。尽管从学习的角度看，信息的传播是双向的，但BP网络的结构仍是单向的，不存在信息反馈，是一种前向型网络。

设有图2所示的3层BP神经网络。其中第层的第个神经元的输入总和为，输出为，第−1层的第个神经元与层的第个神经元的连接权为，则

对于给定的任一输入模式，若网络第层的第个神经元输入误差(来自于第+1层)为，采用梯度最速下降法，使权值沿误差函数的负梯度方向变化，即有

其中：

从而有

对于网络的输出层+1，定义它的第个神经元输出与期望输出d的误差有如下形式：

从而有

对于中间层，它的误差来源于+1层，所以，根据式(11)有

从而，式(15)可写为

由此可以将BP网络的学习算法分成以下2部分。

1) 对于输出层单元，有

2) 对于中间层单元，有

则

由此可计算出式(20)和式(21)的权值修正值，通过多次迭代修正即可以计算网络的最优权值。整个网络学习过程分为2个阶段：第1阶段(信息正向传播过程)，计算输入信息通过输入层经中间层到输出层逐层处理，并得出每个单元的实际输出值；第2阶段(误差反向传播过程)，若输出层未能得到期望的输出值，则组成递归函数计算实际输出与期望输出之间的误差，以便根据此误差来调节权值。2个过程反复交替，直到达到收敛为止。

2 模型试验

网络输入输出参数、隐含层个数及节点数是关系到大地电磁反演效果的重要因素。对水平层状模型进行研究，其模型参数为每层的电阻率和层厚度h，进行一维正演计算时，模型的视电阻率可由理论公式直接计算得到。设频点数为，层状模型层数为，则模型参数个数=2−1。神经网络的输入端为各个不同频点的视电阻率：

输出端为模型参数：

(27)

隐含层的个数和节点数与模型的数量与输入输出参数密切相关，需要依据具体情况来选取。下面分别就2层和3层模型分别进行神经网络训练和反演计算。

2.1 2层理论模型

采用频点数为20的2层水平模型进行研究，则网络输入层节点数为20，输出层节点数(即模型参数个数)为3(即)。令和取值范围均为100~1 000 Ω∙m，1取值范围均为100~1 000 m，每个参数按等间隔取10个值，即和分别取值为100，200，…，900，1 000 Ω∙m，1取值为100，200，…，900，1 000 m。根据排列组合得出1 000组模型，这样，所有2层介质的G型和D型模型都包含在内。由于神经网络的输出函数为S型函数，范围在0~1之间，故在训练及测试过程中对所有数据进行归一化处理。由正演得出的模型参数−视电阻率样本集分别作为网络的输出和输入进行学习训练，用1 000组的4/5即800组数据样本进行网络训练，其余1/5即200组未参与网络训练的数据进行测试反演。

神经网络连接权初始值采用随机值，采用BP算法有可能收敛到局部最优解而不是全局最优。经过50次试验，有38次满足误差精度要求，成功收敛，其余12次不能满足误差精度，收敛成功率为76%。

采用MATLAB神经网络工具箱中BP算法的2种改进算法即Levenberg−Marquardt法和Quasi−Newton法分别对数据样本进行训练，结果表明：对数据量较少的2层模型，Levenberg−Marquardt法收敛速度比Quasi−Newton法的收敛速度更快；对800组数据样本的网络训练时，Quasi−Newton法耗时7 s左右(每次训练时间略不同)，而在同样的参数下，Levenberg− Marquardt法只需2 s左右。

采用1层隐含层，选取不同的隐层节点数进行网络训练，目标误差精度为5×10−3。图3所示为成功收敛时隐层节点分别为30和8时的误差收敛曲线。从图3可看出：不同隐层节点数在网络训练初始时有所差别，但对最终的收敛效果影响不大，经过15次迭代，都能达到误差精度。图4所示为用训练好的网络对测试数据(未训练数据)进行反演的视电阻率，具体模型参数见表1(其中，和1分别为第1层的电阻率和厚度；和2分别为第2层的电阻率和厚度)。图5所示为50组训练参数的理论值与计算值均方误差，图6所示为 10组测试数据的理论值与计算值均方误差，与表1中的10个样本参数一一对应。

1—隐层节点数为8；2—隐层节点数为30

1—理论视电阻率；2—反演视电阻率

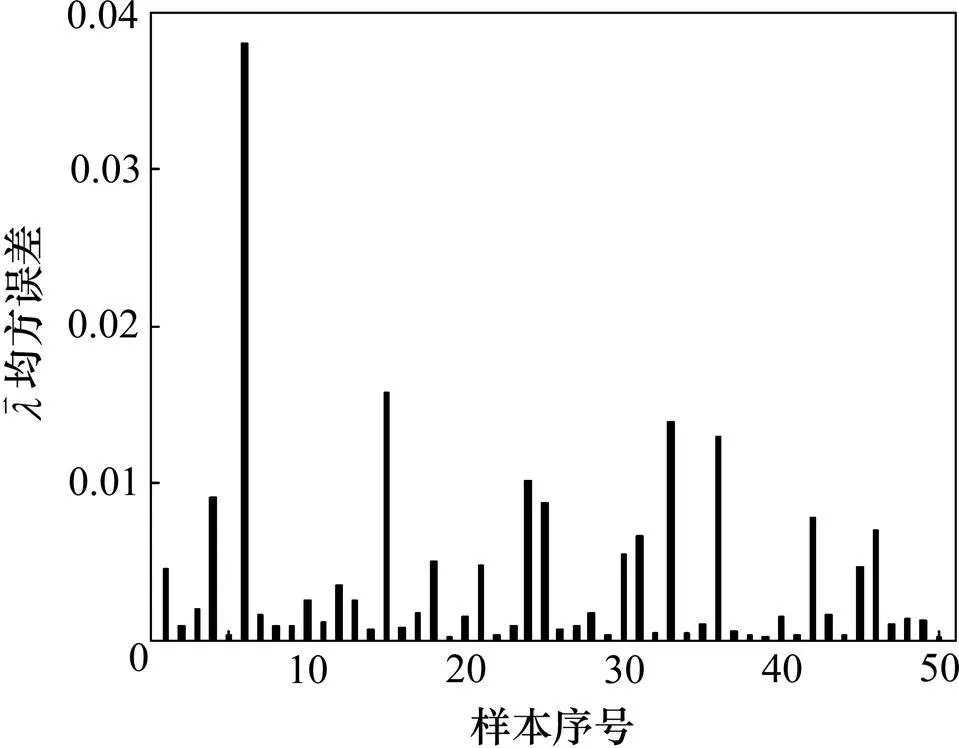
图5 2层模型50组训练均方误差

图6 2层模型10组测试反演均方误差

表1 2层模型10组测试反演数据对比

2.2 3层理论模型

采用频点数为20的3层水平模型进行研究，则网络输入层节点数为20，输出层节点数(即模型参数个数)为5(即1,2,3,1,2)。令1，2和3取值范围为100~1 000 Ω∙m，1和2取值范围为100~1 000 m，每个参数按等间隔取10个值，与2层模型类似，根据排列组合得出105组模型，由此所有3层介质的H型、A型、K型和Q型模型都包含在内。用4/5即8×104组数据样本进行网络训练，其余1/5即2×104组未参与网络训练的数据进行测试反演。

本次3层模型数据同样采用Levenberg−Marquardt法和Quasi−Newton法分别对数据样本进行训练，由于数据量过大，Levenberg−Marquardt法计算所需存储量过大，训练失败。Quasi−Newton法所需存储量较小，能成功收敛(与2层模型网络类似，成功收敛率约为80%)，运行时间为320 s左右。

分别采用1层隐含层和2层隐含层进行网络训练，目标误差精度为5×10−3。图7所示为3层模型网络训练误差收敛曲线。从图7可见：不同隐层数在网络训练初始时有一定差别，但对最终的收敛效果影响不大，经过50次迭代，都能达到误差精度。图8所示为用训练好的网络对测试数据进行反演的一组视电阻率，具体模型参数见表2。图9所示为50组训练数据的理论值与计算值误差，图10所示为 10组测试数据的理论值与计算值误差，与表2中的10个样本参数一一对应。

1—2层隐层，节点数为30和40；2—1层隐层，节点数为50

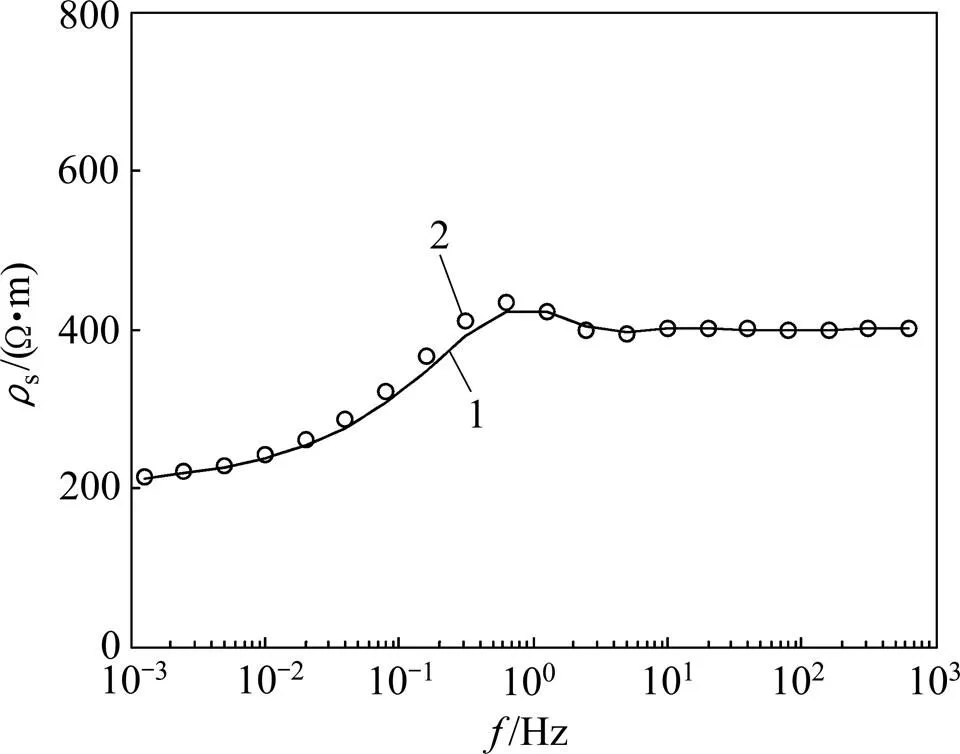
1—理论视电阻率；2—反演视电阻率

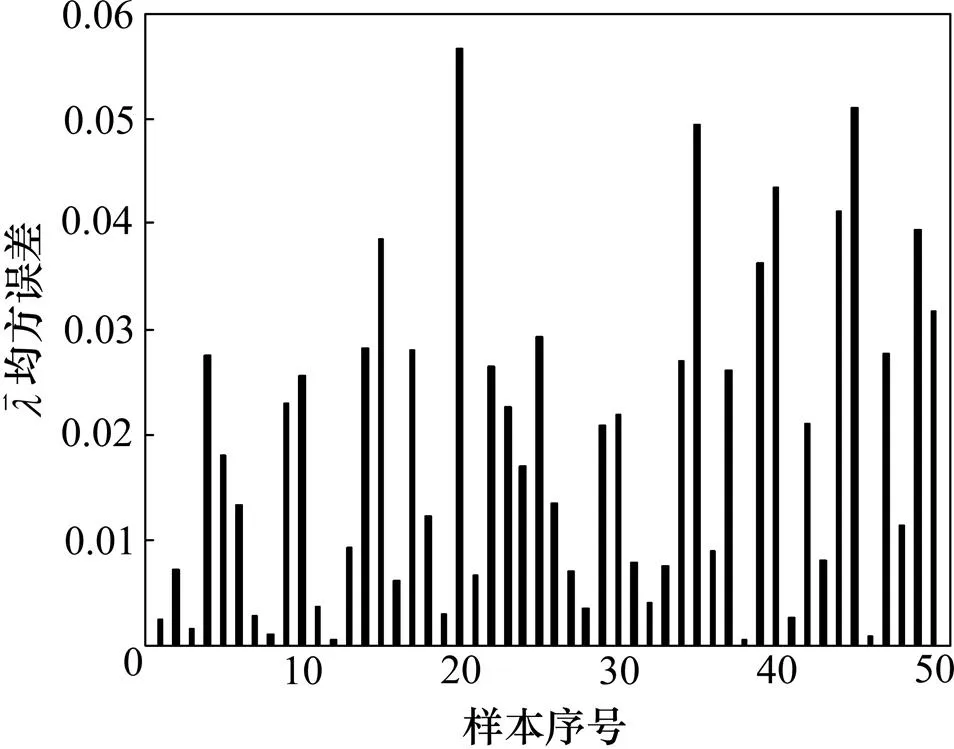
图9 3层模型50组训练均方误差

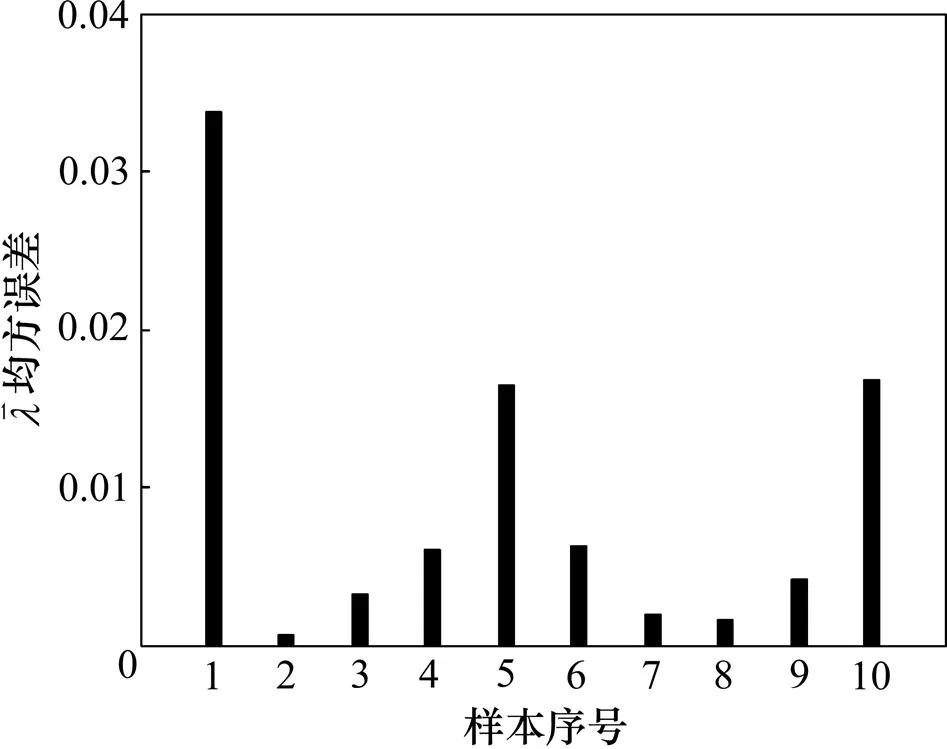
图10 3层模型10组测试反演均方误差

2层和3层模型的神经网络训练和反演结果表明基于神经网络的大地电磁反演的可行性和有效性，但网络训练的成功率还有待提高。

3 实测视电阻率反演

为检验该方法的有效性，选择云南个旧驼峰山矿区2号测线第80~200号点共13个测点的大地电磁视电阻率，经数据处理后利用2.2节中3层模型训练好的网络结构和连接权值进行神经网络反演。

图11所示为矿区2号测线第80号测点实测视电阻率与反演后视电阻率曲线对比，表3所示为第80~200号点共13个测点的3层神经网络反演结果，图12所示为13组反演数据结合地质资料插值平滑后得出拟断面图。从图12可见：第1层电阻率较低，一般为100~200 Ω∙m，推断为中三叠统个旧组马拉格段第2层(T2g22)灰质白云岩，厚度约为200 m；第2层电阻率为次高阻，一般为300~400 Ω∙m，推断为中三叠统个旧组马拉格段第1层(T2g21)白云岩，厚度约为400 m；第3层电阻率为高阻，电阻率一般为600~1 000 Ω∙m，推断为中三叠统个旧组卡房段第6层(T2g16)灰岩夹灰质白云岩中赋存有锡铜矿体。该结果与该区的地质情况基本吻合，表明了神经网络反演方法的可行性和有效性。

表3 实测数据神经网络反演结果

1—实测视电阻率；2—反演视电阻率

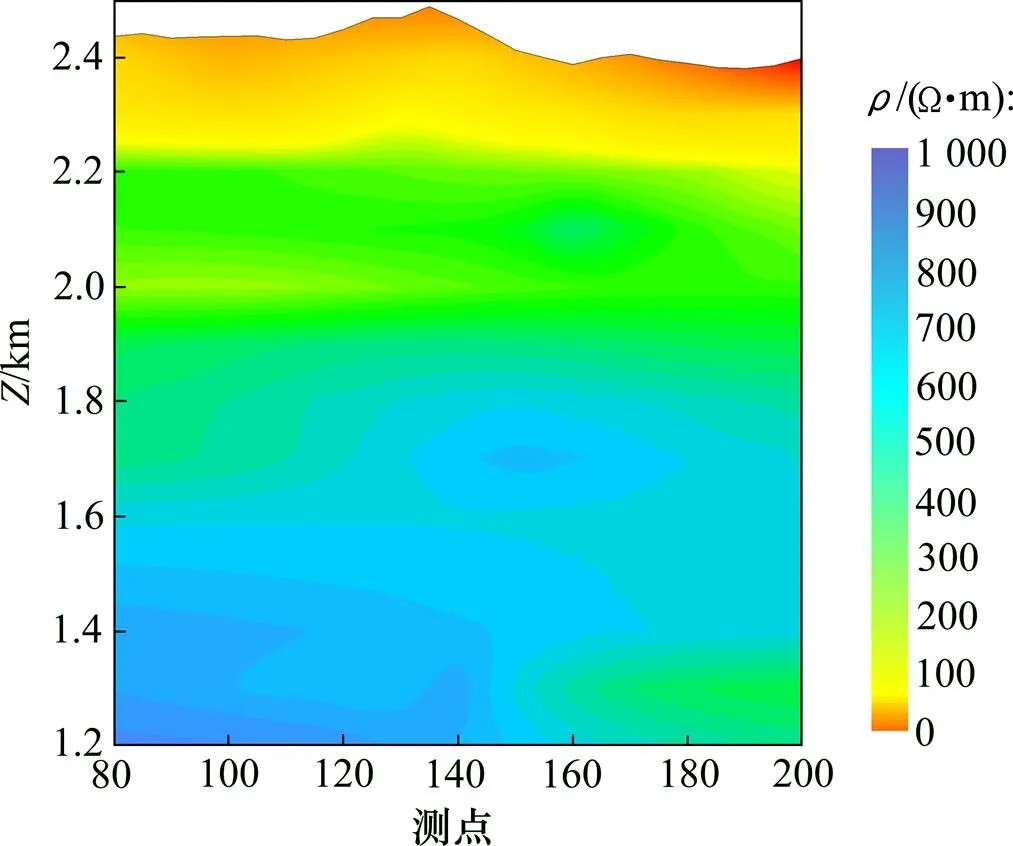
图12 云南个旧矿区实测数据反演拟断面图

4 结论

1) 利用神经网络的非线性映射性可进行大地电磁非线性反演。通过训练已知模型数据，得出网络最优权值，再对未训练的视电阻率进行测试反演。理论计算与实测结果表明该反演方法可在满足误差精度的条件下逼近真实模型。

2) 本算法主要计算在网络训练阶段的耗时。训练好的网络可对类似模型的视电阻率曲线进行实时反演，无需经典反演中的正演计算过程，也无需求解雅克比矩阵，可大大提高反演速度和效率。

3) 神经网络的BP算法采用随机初始权值，有可能使计算收敛到局部最优解而不是全局最优，下一步考虑结合遗传算法等全局优化算法来提高收敛成功率。

4) 二维和三维反演较一维反演在数据量上增加了几个数量级，如何建立相应的网络结构和选择训练数据有待进一步研究。

[1] Robertl P. The magnetotelluric inverse problem[J]. Geophysical Surveys, 1983, 6: 5−25.

[2] Constable S C, Parker R L, Constable C G. Occam’s inversion: A practical algorithm for generating smooth models from EM sounding data[J]. Geophysics, 1987, 52(3): 289−300.

[3] Weerachai S, Egbert G. An efficient data-subspace inversion method for 2-D magnetotelluric data[J]. Geophysics, 2000, 65(3): 791−803.

[4] Smith J T, Booker J R. Rapid inversion of two- and three- dimensional magnetotelluric data[J]. Journal of Geophysical Research, 1991, 96: 3905−3922.

[5] Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174−187.

[6] 陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937−946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937−946.

[7] 徐义贤, 王家映. 大地电磁多尺度反演[J]. 地球物理学报, 1998, 41(5): 704−711. XU Yixian, WANG Jiaying. A multiresolution inversion of one-dimensional magnetotelluric data[J]. Chinese Journal of Geophysics, 1998, 41(5): 704−711.

[8] 谭捍东, 余钦范, John B, 等. 大地电磁法三维快速松弛反演[J]. 地球物理学报, 2003, 46(6): 850−854. TAN Handong, YU Qinfan, John B, et al. Three-dimensional rapid relaxation inversion for the magnetotelluric method[J]. Chinese Journal of Geophysics, 2003, 46(6): 850−854.

[9] 严良俊, 胡文宝. 大地电磁测深资料的二次函数逼近非线性反演[J]. 地球物理学报, 2004, 47(5): 935−940. YAN Liangjun, HU Wenbao. Non-linear inversion with the quadratic function approaching method for magnetotelluric data[J]. Chinese Journal of Geophysics, 2004, 47(5): 935−940.

[10] 柳建新, 童孝忠, 杨晓弘, 等. 实数编码遗传算法在大地电磁测深二维反演中的应用[J]. 地球物理学进展, 2008, 23(6): 1936−1942. LIU Jianxin, TONG Xiaozhong, YANG Xiaohong, et al. Application of real coded genetic algorithm in two-dimensional magnetotelluric inversion[J]. Progress in Geophysics, 2008, 23(6): 1936−1942.

[11] Singh U K, Tiwari R K, Singh S B. Neural network modeling and prediction of resistivity structures using VES schlumberger data over a geothermal area[J]. Computers & Geosciences, 2013, 52(3): 246−257.

[12] Spichak V, Popova. Artificial neural network inversion of magnetotelluric data in terms of three dimensional earth macro parameters[J]. Geophysical Journal International, 2000, 142: 15−26.

[13] 杨立强, 宋海滨, 郝天珧. 基于BP神经网络的波阻抗反演及应用[J]. 地球物理学进展, 2005, 20(1): 34−37. YANG Liqiang, SONG Haibin, HAO Tianyao. Application of impedance inversion based on BP neural network[J]. Progress in Geophysics, 2005, 20(1): 34−37.

[14] 贺懿, 张进, 刘怀山. 基于神经网络的面波迭代反演应用研究[J]. 西南石油大学学报(自然科学版), 2010, 32(1): 40−44. HE Yi, ZHANG Jin, LIU Huaishan. Study on the application of iterative inversion of surface wave based on artificial neural network[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(1): 40−44.

Magnetotelluric inversion using artificial neural network

WANG He1, 2, JIANG Huan1, 2, WANG Liang3, XI Zhenzhu1, 2, ZHANG Daojun3

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China; 2. Marine Marine Exploration and Equation Research Institute, Central South University, Changsha 410083, China; 3. Changsha 5D Geo-survey and Technical Co. Ltd., Changsha 410205, China)

The artificial neural network(ANN) was studied to improve the magnetotelluric inversion operation efficiency and calculation accuracy. The input of neural network was apparent resistivity of the known models, and the output of neural network was the geoelectric parameters. The neural network was trained by back propagation algorithm, which contains the methods of information forward propagation and error back propagation. The best weight of network calculated by the training work was used to test the unknown model patterns, which is the inversion process. The networks for two-layer model and three-layer model were set up respectively. The results show that the neural network inversion is feasible and effective.

magnetotelluric; neural network; inversion

10.11817/j.issn.1672-7207.2015.05.019

P631

A

1672−7207(2015)05−1707−08

2014−06−20；

2014−08−22

国家自然科学基金资助项目(41304090)；大洋“十二五”重大项目(DY125-11-R-03)；中央高校科研业务费资助项目(2012QNZT074) (Project(41304090) supported by the National Natural Science Foundation of China; Project(DY125-11-R-03) supported by Ocean Major during “Twelfth Five Year Plan”; Project(2012QNZT074) supported by Scientific Research Expenses Fund of Central University)

王鹤，博士，副教授，从事电磁法数据处理与反演研究；E-mail: wanghe46@163.com

(编辑 陈灿华)