均值—绝对偏差模型鲁棒优化策略的有效性——基于中国股票市场的实证分析*

赵 庆

(1．东北财经大学研究生学院，辽宁大连116025;2．辽宁对外经贸学院 国际经贸学院，辽宁 大连 116052)

引言

在不确定的金融市场中，由于各种金融产品风险存在差异，因此，如何在兼顾收益与风险的情况下对产品进行组合选择，也就成为投资组合的重要问题。Markowitz(1952)［1］提出了投资组合的均值—方差模型(MV模型)，它相继应用于金融投资分析的不同领域，但是MV模型的缺点也比较明显:(1)对参数的不确定性与估计误差敏感，即均值或方差一点小的扰动都可能完全改变最优投资组合。(2)计算过程复杂，即对于包含n种证券的组合而言，其协方差矩阵计算量大，需要计算n(n+1)/2次。(3)MV模型形式为二次规划模型，其最优解求解比较困难，有时甚至于无法求解。基于上述原因，国内外学者发展了很多其他投资组合模型，其中Konno和 Yamazaki(1991)［2］提出了均值—绝对偏差模型(MAD模型)，该模型利用均值—绝对偏差风险目标函数克服了缺点(1)，同时其线性化模型克服了缺点(2)和(3)。在该模型基础上，国内学者研究出几种衍生模型:康志林(2013)［3］提出了均值—绝对偏差投资组合修正模型，该模型针对投资者对不同收益率资产的偏好，通过引入收益权值系数，直接对各证券的收益离差进行非对称影响分析，重构均值—绝对离差投资组合模型，并将模型转换为线性规划;张鹏(2009)［4］提出具有上下界限制的均值—平均绝对偏差投资组合模型，并运用线性规划的旋转算法进行求解;武敏婷，等(2010)［5］在均值—绝对偏差投资模型中加入风险价值约束，给出了基于VaR约束的投资组合优化模型;刘善存，等(2001)［6］用对策论方法讨论证券组合投资问题，建立了组合投资问题的基本对策模型。

鲁棒性是一个系统面临内部结构和外部环境变化时，能够保持其系统功能的能力。Tetlow(2001)［7］指出:在金融系统中，来自市场波动、汇率变动、利率及资产价格变化等方面的内部变化不确定性，来自自然灾害、国际政治和经济环境变化等方面的外部不确定性，直接影响到金融系统的正常运行，鲁棒性成为能否确保金融系统持续、正常运行的重要因素。金融系统的鲁棒性是金融系统的一个重要属性，而金融系统中的鲁棒优化则是为了实现金融系统的鲁棒而进行的一种优化设计。目前，国内外关于鲁棒优化投资组合的文献也较多，Ghahtarani和 Najafi(2013)［8］基于目标规划方法(Goal Programming Approach)提出多目标函数鲁棒优化模型。Costa和Paiva(2002)［9］在假设已知期望收益率和协方差矩阵边界的条件下，基于线性矩阵不等式方法，研究了鲁棒跟踪误差投资组合优化问题。Zheng和 Liang(2013)［10］在该方法基础上，引入交易费用。高莹和黄小原(2008)提出基于线性矩阵不等式的动态投资组合鲁棒策略。张春梅和陈志平(2013)［11］针对有限情形的不确定集、正态分布等情形提出了一种满足齐次性、次可加性和单调性的相对鲁棒的CVaR风险度量。

对于鲁棒优化方法而言，从模型的数学描述角度看，解决内部结构变动问题时，一种是约束条件参数的不确定性，另一种是目标函数参数的不确定性。鲁棒优化解决外部环境变化时，主要是外界不确定性扰动。到目前为止，鲁棒优化方法主要有三种方法。第一种方法是Soyster(1973)［12］提出的，他在鲁棒优化方面做了开创性的工作，提出了一个线性优化模型来求得一个对所有属于一个凸集的数据均可行的解。但这个推断模型产生的解在某种意义上太保守，为了保证鲁棒性，放弃了很多的标称问题的最优性。第二种方法是Ben-Tal和Nemitovski(1998)［13］提出的新的鲁棒优化处理不确定性环境方法，对处理过度保守性作出了努力，将鲁棒优化应用到具有椭球不确定集合的线性规划问题中，得到了二次锥规划，但由于其非线性性，其求解较为复杂。第三种方法是 Bertsimas和 Sim(2004)［14］专门为多种不确定性提出的一种方法，是通过生成的线性鲁棒对应来控制解的保守性水平即可以调节鲁棒水平(Protection Level，PL)的方法，并且得到的是线性模型，相比第二种方法也更容易求解，并且该方法也很容易拓展到离散优化问题。Moon和Yao(2011)［15］基于第三种方法提出均值—绝对偏差模型的鲁棒优化线性模型(RMAD模型)。

本文在 Moon和 Yao(2011)［15］的基础上，考虑我国证券市场的实际情况并且在不失一般性基础上，提出了适合我国投资组合管理的、基于鲁棒优化的简化RMAD模型，并且利用MATLAB求最优解。同时，将 RMAD模型的最优解与张鹏(2009)［4］、武 敏 婷，等 (2010)［5］、刘 善 存，等(2001)［6］的研究结果进行比较分析，根据投资组合绩效分析，RMAD模型优于上述三种模型。

一、模型描述

(一)均值—绝对偏差模型(MAD模型)

假设证券投资组合中包含n种证券;第j种证券的回报率为 rjt(j=1，2，…，n，t=1，2，…，T);t为投资组合时间间隔;T为投资组合时间跨度，即有T个时间段;xj为投资组合中第j种资产投资权重;ρ为投资者对该投资组合的期望收益率;rj为第j种资产期望收益率，rj=E［rjt］(即 rjt的算术平均数);uj为该投资组合第j种资产投资权重xj的上限;C为该投资组合投资额。根据 Konno和 Yamazaki(1991)［2］提出的 MAD 模型(1)—(4):

由于(1)—(4)为非线性模型，求解复杂，故此在原模型基础上通过引入辅助变量yt=可以将其转化为线性MAD模型(5)—(10):

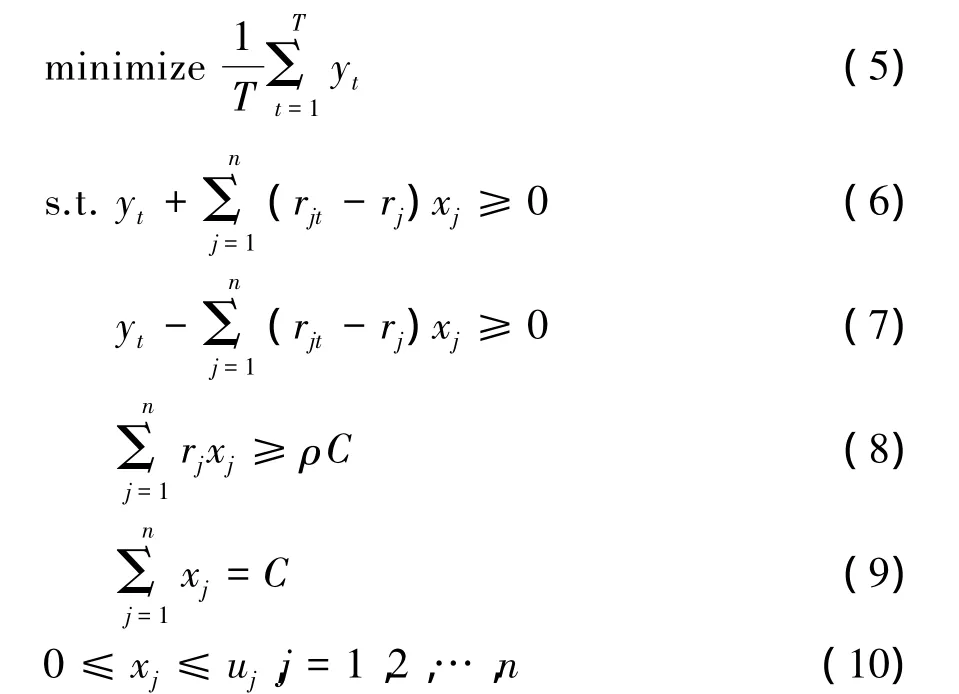
线性模型(5)—(10)求解容易，如文献［3］［4］［5］均是以该模型为基础研究衍生模型。

(二)均值—绝对偏差模型鲁棒优化模型(RMAD)

Moon 和 Tao(2011)［15］基于 Bersimas 和 Sim(2004)［14］鲁棒优化方法给出了MAD模型鲁棒优化模型:Γ0为鲁棒模型保护水平，Γ0∈［0，］，J0≡{1，2，…，n}，Γ0值越大意味着鲁棒水平越高，对于给定鲁棒模型保护水平Γ0，考虑子集S0满足S⊆J= Γ 。∧

00和 S00对于给定子集S0和常数rv，v∉SJ。w≤00j为可行集 xj的上界，即为投资者期望投资组合模型回报率ρ与第j种资产=ρ－r。期望收益率rj的偏差，即j则 MAD 模型鲁棒优化模型(RMAD模型)为(11)—(17):

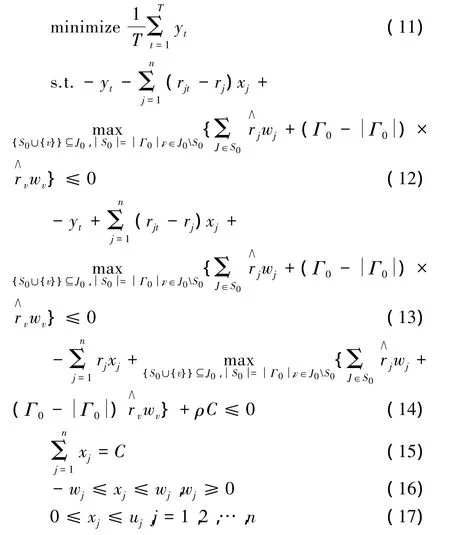
模型(11)—(17)虽为RMAD模型，但是其作为非线性模型很难求解。故此，希望能转化为线性模型以方便求解。在RMAD模型线性化过程中，选取人工变量z0作为约束变量;选取人工变量 pj作为 zj≤1，∀j∈J0约束变量，其中 z0、pj为该模型未知变量，需要求解;其余变量含义均与上相同。RMAD线性模型为(18)—(27):

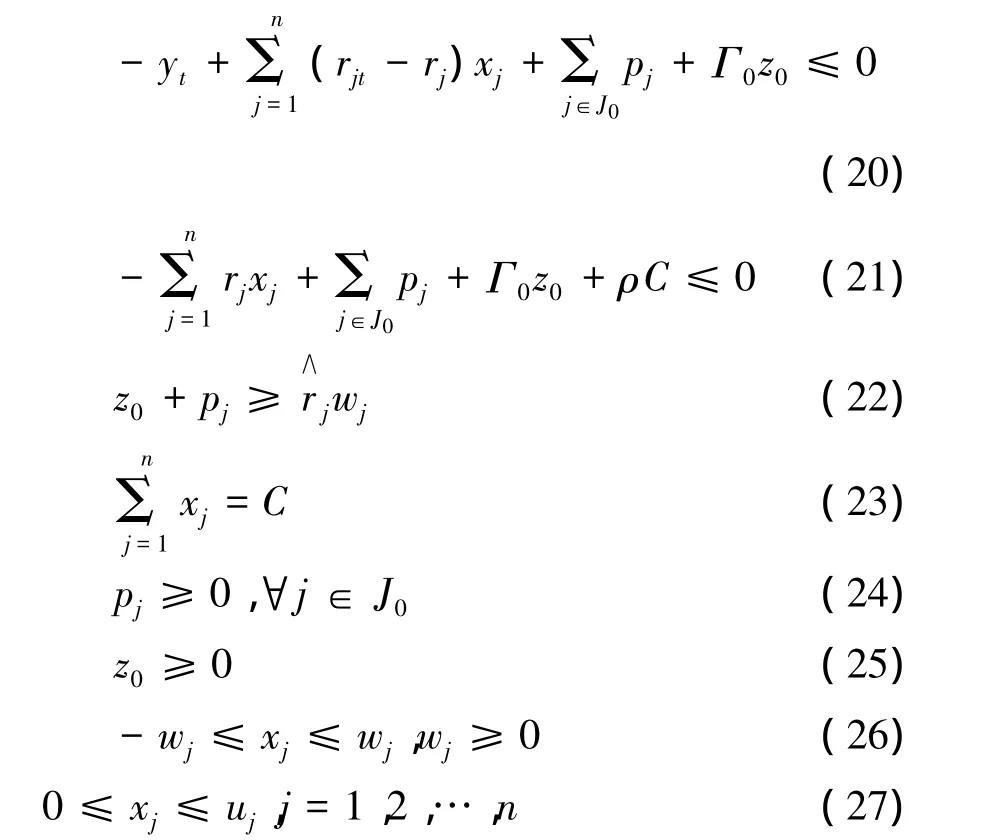
本文结合中国资本市场实际情况并且在不失一般性基础上，简化上述模型。设定投资额C=1，则xj则代表投资组合第j项资产权重;并且中国股票市场不存在卖空机制，故xj≥0，假设wj=1，设定0≤uj≤1，即 0≤xj≤min(uj，wj);则 RMAD 模型简化为(28)—(36):

此线性规划可用MATLAB linprog函数求解。

二、实证分析

(一)数据描述

为方便与张鹏(2009)［4］、武敏婷，等(2010)［5］、刘善存，等(2001)［6］的模型进行比较，故此采用与上述文献相同数据，如表1所示，6种证券在8个时期的收益率数据。

表1 6种证券在8个时期收益率数据

(二)线性RMAD模型求解方法

MATLAB是具有很强数值计算、符号运算、仿真和图形显示功能的计算机数学语言。MATLAB中解线性规划问题的函数是linprog。函数linprog标准调用格式为:［x，fval］=linprog(f，A，b，Aeq，beq，lb，ub)，用于求解问题:其中将最优目标值返回到变量fval中。

为将RMAD模型(28)—(36)转换为linprog函数标准形式，在本文中将linprog函数中未知量x设为16×1矩阵即:

则linprog函数标准形式(37)中函数fT为1×16矩阵:

取鲁棒保护水平(PL)Γ0=3，投资组合期望收益率ρ=0.03。可将式(29)—(30)共计23不等式转换为linprog函数标准型式(38)，矩阵A为23×21矩阵，b为23×1矩阵:

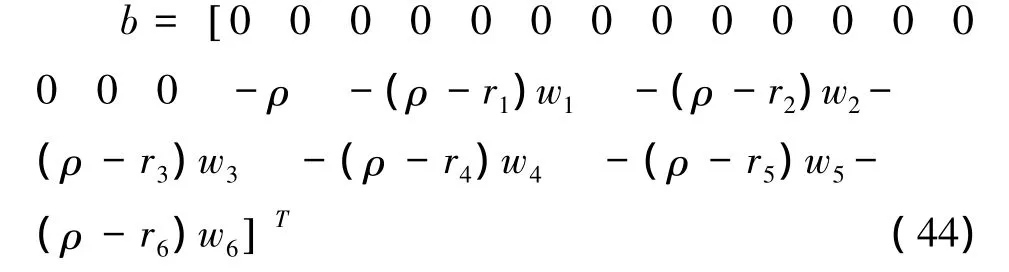
式(33)⇒x1+x2+x3+x4+x5+x6=1转化成linprog标准型式(39)，则 Aeq为 1×21 矩阵，beq为 1×1 矩阵:

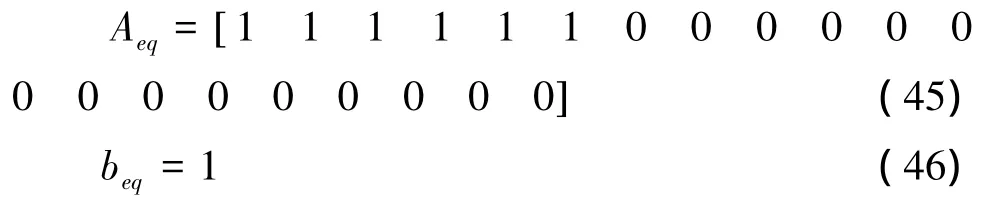
式(34)—(36)转换为linprog函数标准型式(40)，则 lb、ub均为 21×1 矩阵:

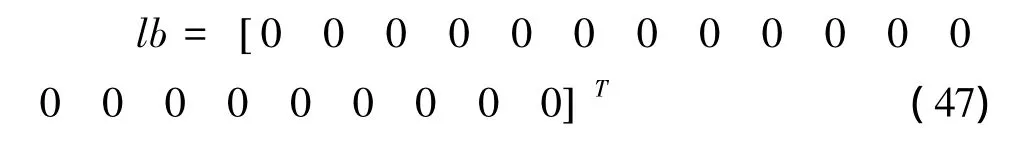
其中inf代表+∞。

综上所述，利用MATLAB 7．0 linprog函数求解方程(43)—(48)最优解，同时将RMAD模型最优解与张鹏(2009)［4］、武敏婷，等(2010)［5］、刘善存，等(2001)［6］最优解比较如表2所示。为衡量金融资产组合的绩效表现，本文采用与康志林(2013)［3］相同评价方法，投资组合绩效=收益/风险。其中武敏婷等(2010)［5］根据投资组合绩效评价方法，从结果中选取最好一组的情况。

表2 投资组合最优解比较分析汇总

根据表2投资组合绩效分析，可以看出，张鹏(2009)［4］组合收益率最高但是风险也最大，投资组合绩效最低，刘善存，等(2001)［6］与武敏婷，等(2010)［5］投资绩效相差不大，而本文所采用的RMAD模型要比以上3种投资组合模型效果显著。

三、结论

本文在Moon和Yao(2011)的基础上，结合我国证券市场的实际情况并且在不失一般性基础上，提出了适合我国投资组合管理的、基于鲁棒优化的简化RMAD模型，填补了关于鲁棒投资组合的研究;并且运用新的求解方法，利用MATLAB对其线性模型求最优解，进一步验证了MATLAN linprog函数求解线性规划模型的有效性和快捷性。同时，将RMAD 模型的最优解与刘善存，等(2001)［6］、张鹏(2009)［4］、武敏婷，等(2010)［5］的结果进行投资组合绩效分析，证明简化RMAD模型从收益与风险角度而言明显优于上述三种模型。

［1］MARKOWITZ H．Portfolio Selection［J］．The journal of Finance，1952，7(1)：77-91．

［2］KONNO H，YAMAZAKIH． Mean-absolutedeviation portfolio optimization model and its applications to Tokyo stock market［J］．Management Science，1991，37(5)：519-531．

［3］康志林．均值—绝对离差投资组合修正模型［J］．华侨大学学报(自然科学版)，2013，33(2)：83-88．

［4］张鹏．均值—平均绝对偏差投资组合模型与优化［J］．统计与决策，2009(1)：14-15．

［5］武敏婷，孙滢，高岳林．基于VaR约束的均值—绝对偏差投资组合优化模型及实证研究［J］．2010(3)：156-158．

［6］刘善存，汪寿阳，邱菀华．一个证券组合投资分析的对策论方法［J］．2001，32(5)：88-92．

［7］TETLOW R，MUEHLEN P．Robust monetary policy with misspecified models：does uncertainty always call for attenuated policy? ［J］．Journal Economical Dynamics Control，2001，25(7)：911-949．

［8］ALIREZA GHAHTARANI，AMIR ABBAS NAJAFI．Robust goal programming for multi-objective portfolio selection problem［J］．Economic Modelling，2013，33(5)：588-592．

［9］COSTAOLV ，PAIVAAC ．Robust portfolio selection using linear-matrixinequalities ［J］．JournalofEconomic＆Control，2002，26(6)：889-909．

［10］DONG ZHENG，XI-KUN LIANG．Optimization of tracking error for robust portfolio of risk assets with transaction cost［J］．iBusiness，2013，(5)23-26．

［11］张春梅，陈志平．基于CVaR的相对鲁棒投资组合问题研究［J］．工程数学学报，2013，30(4)：525-534．

［12］SOYER A L．Convex programming with set-inclusive constraints and applications to inexact linear programming［J］．Operations Research，1973，21(5)：1154-1157．

［13］BEN-TAL A，NEMIROVSKI A．Robust convex optimization［J］．Mathematics of Operations Research，1998，23(9)：769-805．

［14］BERSIMAS D，SIM M ．The price of robustness［J］．Operations Research，2004，52(1)：35-53．

［15］YONGMA MOON，TAO YAO．A robust mean absolute deviation model for portfolio optimization ［J］．Computers ＆Operations Research，2011，38(12)：1251-1258．