基于模糊控制模型的电压暂降监测装置优化配置

唐亚迪，徐永海，洪旺松

（华北电力大学 电气与电子工程学院，北京 102206）

0 引言

电压暂降对敏感设备的影响是国外发达国家最为关心的电能质量问题[1-4]，在国内其关注程度也越来越高[5-6]。安装电能质量监测装置是获取电压暂降信息、进行相关问题分析的重要手段。但从经济性方面考虑，一般只在特定的重要母线上安装电能质量监测装置。因而如何在适当的母线上，在保证不遗漏重要数据的基础上安装最少的监测装置，利用其获取的电压暂降信息，进行全网整体电压暂降特性的分析，是一个重要的问题。

在以往的研究中，文献[7]首先提出了监测点优化配置的概念并且建立了基于可观测区域（MRA）的优化模型，在此基础上文献[8-10]运用各种线性优化方法进行优化，但文献[8-10]中的优化模型完全依赖于严格的暂降阈值，仅以监测点最小个数为目标函数，这样往往得出多个可行方案而无法给出最优结果。文献[11-12]运用故障识别法进行优化模型的建立，将MRA转变为故障可识别矩阵，由于监测目标提高到故障点可定位，可能会使监测装置安装数量较多。

针对电压暂降的监测问题，本文建立了基于模糊模型和离散粒子群优化（BPSO）算法的优化模型，提出了模糊边界的概念，充分利用电压暂降特征值信息，不仅给出了监测点的观测区域，并且给出了每条母线在该区域内的影响值大小，有助于选择最优的配置方案。采用所提出方法，首先基于短路故障分析中得到的数据建立基于模糊边界的电压暂降观测域；建立 Mamdani模糊模型和Sugeno模糊模型，其中Mamdani模型用于计算各个母线的观测指数，Sugeno模型用于构造优化的目标函数，目标函数既能反映监测点数目又能反映方案的优劣；对于建立的目标函数，采用具有收敛速度快、鲁棒性好等性能的BPSO算法进行优化，得到最少监测装置数量和最优安装位置的方案；最后，本文以IEEE30节点系统作为算例，验证了所提出方法的优越性。

1 电压暂降幅值计算

图1 电力系统短路故障计算模型Fig.1 Model of power system short circuit calculation

在电压暂降发生原因中，短路占了绝大多数，本文仅以短路故障来分析计算电压暂降的幅值。如图1所示，假设m为监测点，短路故障发生在电网中线路 g-h上的 f点处，故障阻抗为zf，故障点f和g点的距离为l，定义：

其中，Lgf为节点g与故障点f间的距离；Lgh为线路g-h的总长度。由上式可知当l在0～1之间变化时表示故障点f的位置从节点g向节点h移动。

m与f之间的互阻抗和f的自阻抗分别为：

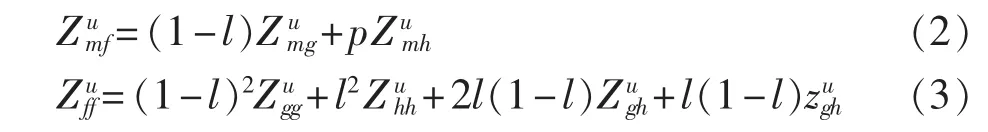
其中，u为阻抗的次序，当u取0、1、2时分别表示该阻抗为零序、正序和负序阻抗；Zumg和Zumh分别为节点m、g和节点m、h之间的互阻抗；Zugg和Zuhh分别为节点g和节点h的自阻抗；Zugh为节点g、h间的互阻抗；为线路g-h的阻抗。

设各节点故障前电压均为1p.u.，f点发生不同类型短路故障时，母线m的电压暂降幅值计算公式如下。

（1）三相短路故障。

（2）单相接地短路故障。

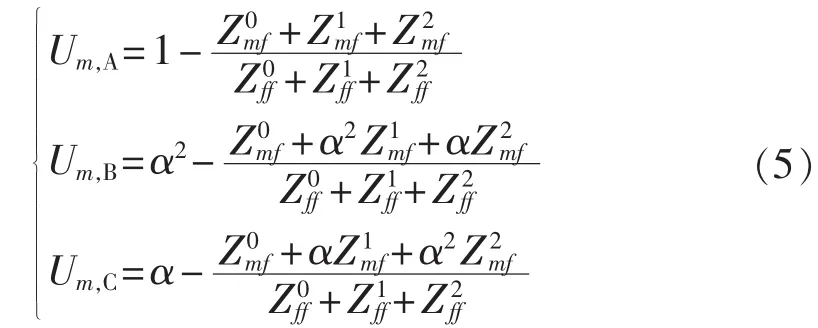
其中，α 为算子，α=ej120°。

（3）两相短路故障。

（4）两相接地短路故障。

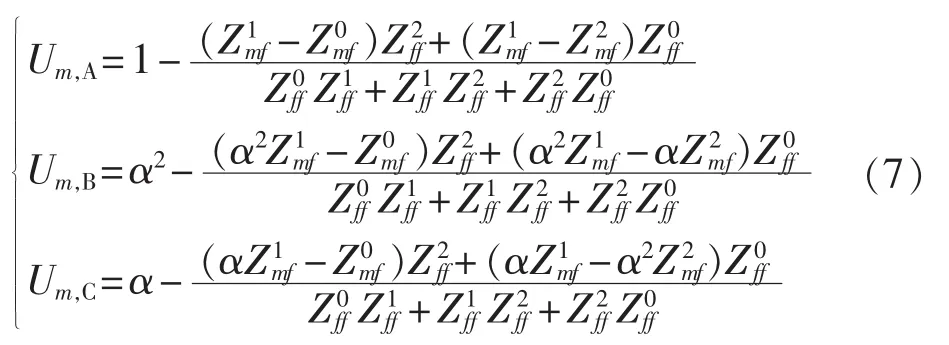
由以上计算方法可得到不同故障类型下的电压凹陷域矩阵。用一个N×F的矩阵表示，N和F分别为系统母线数和故障点数。

2 传统方法的不足和改进

2.1 基于MRA的优化方法及其不足

几乎所有的研究中都依赖一个严格的电压阈值来判别电压是否发生暂降，通过比较阈值和短路计算所得的电压幅值得到电压暂降MRA。MRA是指系统中发生故障时，使某一监测点发生电压暂降的故障点所在区域。MRA实质上是凹陷域的另一种表达形式。与凹陷域矩阵相对应，MRA为一个N×F的矩阵。

其中，i为观测母线，j为故障点；t为故障类型，如上所述，分为三相短路、单相短路、两相短路和两相接地短路故障，每种故障建立一个对应的MRA；Mt，ij表示在某种故障下，故障点j发生故障时，监测点i能否监测到暂降，其值为1表示可监测到暂降，其值为0表示不能监测到暂降；p为电压暂降阈值；Vij为凹陷域矩阵Vdip中第i行第j列的值，表示故障点j发生短路故障时节点i的电压有效值。定义向量X为N维向量，各维xi表示母线i的监测点安装情况。

为了确保每个故障都要被监测点监测到，算法要保证对于MRA中任意第i行元素，X中元素满足以下约束条件：

其中，t为故障类型；bj为每个故障点需要至少被观测到的次数。

传统优化配置中目标函数为监测点数目：

对于电压暂降而言，MRA内发生的能引发该母线电压暂降的短路故障都应该触发该母线上的监测装置，而在监测域外发生的故障则不应该触发该母线上的监测装置。因而这种优化方法得到的监测装置配置依赖电压暂降阈值，并且由于目标函数单一，传统的方法往往会得出多个可行方案，而无法给出最优方案。

为了说明传统优化配置方法的缺点，用传统方法对文献[13]中的13节点系统进行电压暂降监测点的配置，图2所示为三相短路故障时2种配置方案示意图。2种方案均可满足全网暂降可观测，但是传统方法无法给出哪一个方案更好。

根据对该系统短路计算所得的电压暂降幅值可知，图2（a）所示的方案中监测点13的可观测区域内，最大电压暂降幅值为0.89p.u.（故障发生在节点8时）；图2（b）所示的方案中监测点12的最大电压暂降幅值为0.78p.u.（故障发生在节点6时）。由于在实际情况下暂降值会受到各种因素影响（如接地电阻等）而改变[7]，当节点8发生故障时，节点13的电压暂降计算值0.89p.u.接近阈值0.9p.u.，若实际值大于0.9p.u.，则不会触发监测点13，而节点8又不在监测点7的MAR内，最终将导致节点8的故障无法被监测到。然而监测点12的观测域中最大电压暂降值0.78p.u.远小于监测点13的0.89p.u.，说明监测点12几乎不会因为实际暂降值的升高而无法监测到该点故障，因此图2（b）中的方案更加可靠。在本文所提出方法中将根据各个监测点MRA内的电压暂降幅值对监测点进行评估，并通过对目标函数的重新建立，实现配置方案的自主选择。

2.2 模糊边界可观测域建立

本文用一种模糊阈值来替代传统的严格阈值。某监测点的MRA如图3所示，图3中严格的边界仅仅指出了哪些故障点在该母线的观测范围内，而图4中的模糊阈值不仅给出了监测点的MRA还给出了该区域内故障点的影响程度。

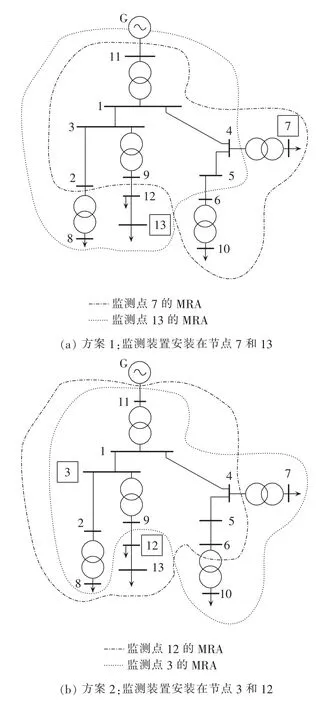
图2 不同的监测点分布方案Fig.2 Different monitoring point arrangements

图3 严格阈值Fig.3 Strict threshold

基于模糊阈值建立的模糊电压暂降可观测区域称为MMRA。每种故障建立一个对应的MMRA。MRA是有明确边界划分的，只有2个部分，元素值为0 或 1。而 MMRA 有 3 个部分，为 I（In）、B（Boundaries）和O（Out），其中In是完全在监测区域的故障点，Boundaries是在模糊阈值区域的故障点，Out包括监测区域之外以及高于传统阈值的点。

图4 模糊阈值Fig.4 Fuzzy threshold

为了说明模糊阈值的含义，上述14节点系统的监测点13的MMRA如图5所示。图中的区域1是监测点13明确的MRA，区域1内故障点引起的监测点13的电压暂降值小于等于0.8p.u.；区域2则是模糊边界域，区域2内故障点引起监测点13的电压暂降值范围为0.8～0.9p.u.。

图5 监测点13的模糊可观测区域Fig.5 MMRA of monitoring point No.13

3 优化模型的建立和算法实现

3.1 目标函数

传统的优化配置方法中通常通过监测点的数量来对比配置结果，没有考虑监测点的观测能力。本文通过运用MMRA，引入监测点观测指数D表示监测点的观测能力。D的大小由MRA内最小的电压暂降值、MRA内电压暂降平均值和MRA内最大的电压暂降值决定。

由2.1节的分析可知，MRA内的电压暂降值越低，该观测点越可靠，受外界干扰越小。因此，监测点的D越小，该点观测能力越好，越不容易忽视导致暂降幅值较大的故障点。

通过建立Mamdani模糊模型[14]计算得到每条母线（候选监测点）的D。一般情况下，监测点发生故障时所能检测到的最小电压暂降幅值均为0（假设故障发生在监测点时接地电阻为0），因此，本文中考虑电压暂降幅值最大值Umax和电压暂降平均值Uave作为输入变量，输出变量就是该监测点的观测指数D。

为了使输入输出量模糊化，本文中输入变量电压幅值最大值Umax和平均值Uave的模糊集采用MMRA中的集合分布：｛I（In），B（Boundaries），O（Out）｝；输出变量 D 的模糊集采用｛TB（真大），WB（弱大），M（中等），WS（弱小），TS（真小）｝。 输入和输出的隶属度函数分别如图6、7所示，模糊规则表如表1所示。

图6 电压幅值最大值和平均值的隶属度函数Fig.6 Membership function of maximum and average voltage amplitudes

图7 观测指数的隶属度函数Fig.7 Membership function of observation index

表1 模糊控制规则表Table 1 Fuzzy control rules

上述模型是基于单一故障类型下建立的，综合考虑各种故障，取某母线在4种故障类型的模型下得到的D的平均值，即可得到该母线的综合观测指数Dgi，且Dgi越小，表示该母线MRA内的整体电压暂降值越低，则监测能力越好。

Sugeno模型[15]能够用较少的规则数描述给定的未知系统，而且其结论部分采用线性模型描述，这使复杂的输入以线性关系输出，因而本文用它来建立目标函数。以监测点个数为输入变量个数，观测指数为变量值，输出为各监测点观测指数的线性函数。该模型可以由1组If-Then的模糊规则来表述，每条规则代表1个线性子系统。假设共有K条模糊控制规则，其中第k条规则Rk可表述为：

模糊系统的输出量为每条规则的输出量的加权平均：

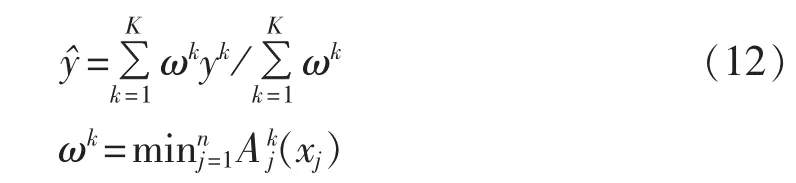
其中，K 为规则数目；n 为输入变量个数；Dg=[Dg1，Dg2，…，Dgn]为n维的输入向量；为系统输出。

输入变量各母线观测指数的模糊集采用｛B（大），M（中），S（小）｝，输入隶属度函数如图8所示。

图8 母线综合观测指数的隶属度函数Fig.8 Membership function of comprehensive observation index for bus

通过模糊控制系统的输出函数，可构造在系统有n个监测点时的优化目标函数为：

该目标函数为2项相乘的复合函数，可以同时反映当前配置方案的监测点个数和方案的好坏程度。从函数中可以看出，即使在监测点个数相同的情况下，不同配置的目标函数也不相同，而且目标函数越小该方案越好，从而可以得到最优方案。

3.2 约束条件

为了保证在任意故障类型下每个故障至少能被1个监测点观测到，建立全局可观测矩阵：

其中，3p、1p、2p和2pg分别表示三相短路、单相短路、两相短路和两相接地短路故障。

则该优化问题应满足以下约束条件：

其中，N为系统母线总数；F为故障点数。

3.3 基于BPSO算法的优化配置

电压暂降监测装置优化配置问题属于典型的离散型、非线性问题。与已有的优化设计模型，如整数线性规划法、遗传算法等相比，粒子群优化算法具有依赖的经验参数少、收敛速度快等优点，但是基本粒子群算法是解决连续性问题的有效方法，不适用于离散问题，因此，本文应用BPSO算法进行优化。

BPSO 算法[13]最早由 Kennedy 和 Eberhart在基本粒子群优化算法的基础上提出，该方法使得粒子群优化算法能够更好地解决离散组合优化问题。

BPSO算法中，粒子向量变为由0和1组成的二进制字符串，即粒子位置的搜索空间变为n维二进制空间。其速度的更新方法与基本粒子群优化算法相同，而位置更新公式变为：

其中，d+1为当前的迭代次数；ρ为0～1的随机数；vij（d+1）为本次迭代中更新后的速度。

由此可见，参数s在0～1间取值的概率取决于粒子速度的大小：若s的值接近于1，则s＞ρ的概率也就越大，其粒子将更可能被选择为1；反之，若s接近于0，则粒子的位置更可能被选择为0。

为了避免BPSO算法易陷入局部最优的缺陷，本文引入自适应惯性权重。小的惯性因子ω′有利于延缓收敛速度，不会出现振荡现象，但是小的惯性因子将缩小搜索空间，容易陷入局部最优；而大的惯性因子可以使粒子的速度增大，增强全局的搜索能力，但容易导致过早收敛。因此，本优化问题中采用一种自适应权重选择法：

其中，minω′、maxω′分别为惯性权重ω′的下限和上限值，一般取值在（0，1）之间；fk为第 k个粒子当前的适应度值；gkd为当前全局最优值；favg为所有个体适应度值的平均值。

BPSO算法中以式（9）给出的N维向量X为状态变量，即粒子群中每个粒子为一个二进制表示的N维向量，每个粒子表示一种配置方案。

本文所提出的电压暂降监测点优化配置流程如图9所示。

图9 电压暂降监测点优化配置流程图Fig.9 Flowchart of optimal voltage-sag monitors allocation

4 算例分析

本文对IEEE30节点系统进行电压暂降监测点的优化配置，IEEE30节点系统接线图如图10所示，该系统包括6个电源、4台变压器、30条母线以及37条输电线路。

图10 IEEE 30节点系统接线图Fig.10 Wiring diagram of IEEE 30-bus system

在电压暂降幅值计算中不能忽略发电机阻抗对短路分析的影响，发电机阻抗通过发电机出力和节点负载计算得到。为了保证优化配置的精度，在每条线路上以等间距取5个故障点作为虚拟故障点。监测装置候选安装点为系统内30条母线。

在MATLAB环境下对该系统进行仿真，BPSO算法中初始种群设为30，最大迭代次数为200次。

IEEE30节点系统各母线监测指数如表2所示，最佳的5个配置方案如表3所示。

从表3可以看出，5个最佳配置方案的监测点个数并不完全相同，前3个方案只需要安装2个监测装置，后2个方案需要3个监测装置。另外，前3个方案只有1个监测点是不同的，即母线7、母线5和母线6，从表2中可以看出，母线7、母线5和母线6的观测指数分别为 0.3650、0.4195和 0.4218，因此，母线7具有更好的观测能力，方案1的目标函数值（即每个粒子的适应度值）也更小，方案1为最优方案。

表2 系统各母线综合监测指数Table 2 Comprehensive observation index of buses

表3 采用本文方法的监测点最优配置结果Table 3 Optimal allocation of monitoring points by proposed method

为了直观地比较方案1和方案2，图11给出了2个方案中不同监测点母线7和母线5在三相短路故障下（由于MRA是在同一故障类型下形成的）的MMRA。

图11 不同监测点在三相短路故障下的模糊可观测区域Fig.11 MMRA of different monitoring points during three-phase short circuit fault

图11（a）和图11（b）所示分别为监测点母线 7和母线5的MMRA。图中各区域含义与图5中相同，区域1内故障点引起监测点母线的电压暂降值小于等于0.8p.u.；区域2是模糊边界域，该区域内故障点引起监测点母线的电压暂降值范围为0.8～0.9p.u.。从两图对比可以看出，图11（a）中分布于区域1的故障点明显多于图11（b），具体故障点分布情况和电压暂降幅值信息如表4所示，表中电压均为标幺值。

从表4可以看出，监测点母线7的MMRA内引起电压暂降的平均值较母线5的平均值小1.183p.u.，最大值也比母线5小。从MRA内引起暂降的故障点数量来看，监测点母线7在区域1内的故障点为62个（包括母线和线路上虚拟故障点），远远多于母线5的18个，即母线7的MRA内引起其电压暂降小于等于0.8p.u.的点集中并且数量很多，这些故障点易被监测，不容易被忽视；而监测点母线7在区域2内的故障点明显少于母线5，即模糊边界内大于0.8p.u.的点较少，产生误判的机会也相对减少。根据2.1节的分析可知，监测装置安装在母线7较母线5有明显的优势。

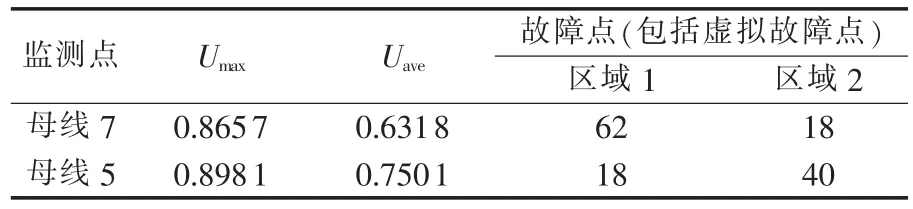
表4 三相短路故障时监测点母线7和母线5可观测域内故障点分布和电压暂降特征量信息Table 4 Fault point distribution and voltage-sag characteristics in MRA of monitoring point Bus 7 and Bus 5 during three-phase short circuit fault

5 结论

本文将模糊控制模型应用到电压暂降监测点优化配置中，充分运用了电压暂降特征值信息，提出了模糊阈值和观测能力指数的概念，并且应用适用于离散问题的BPSO算法实现了优化配置。通过对IEEE30节点标准测试系统的仿真计算以及对结果的分析表明，与传统方法相比，所提出方法对阈值依赖小，并且能够给出配置方案的排序，对于最终的配置方案确定提供了重要依据。