含多微源的微电网离网运行小信号稳定性分析

李 洋，张 辉，苏 冰，贺大为，张玉治，柴建云

（1.西安理工大学 电气工程系，陕西 西安 710048；2.西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710049；3.清华大学 电机工程与应用电子技术系，北京 100084）

0 引言

风力发电和光伏发电等大量功率输出不确定、不稳定且不可调度的微源并入大电网，对电网运行、控制、保护等方面产生了深刻的影响，故包含分布式发电、储能、负荷等的微电网成为国内外研究热点[1-3]。

微电网（尤其是离网模式）能否可靠运行的重要问题之一是能否保持小信号稳定[4]。微电网的小信号模型不仅要考虑传统的同步发电机模型，还需将含有电力电子接口的微源以及网络参数的影响考虑在内，这使得微电网小信号干扰的分析复杂度增大。文献[2]分析了逆变型分布式发电的微电网小信号动态模型，为控制器参数的优化设计提供依据。文献[5]建立了电压源换流器（VSC）的全阶模型，详细阐述了PV控制器的设计方法、P-f下垂控制器及功率限制环节的设计方法和Q-U下垂控制器的设计方法。文献[6]建立了包含光伏电池、燃料电池、微燃机的微电网小信号干扰分析模型，各逆变器首先在本地坐标轴上单独建立模型，然后合并到统一坐标轴上。该模型考虑了逆变器的低频和高频动态、网络和负载动态，并采用灵敏度分析来获取控制参数。文献[7]提出了含同步发电机和逆变器接口的微电网小干扰分析的降阶模型，将各部分统一到公共坐标轴上形成全微电网模型。

本文建立包含同步发电机和VSC接口的微电网小信号干扰机电暂态分析模型；在PQ和PV不同下垂控制策略时，采用特征根分析方法分析网络参数以及控制器参数变化对微电网稳定性及动态特性的影响，构建MATLAB／Simulink时域仿真模型进行仿真研究。

1 微电网建模

1.1 微电网结构

本文构建的典型微电网结构如图1所示。微电网额定电压为380 V，包含的典型微源为风力发电机和储能装置，分别通过同步发电机和VSC并入电网，负载为R-L。

图1 微电网小信号稳定性分析结构图Fig.1 Structure of microgrid for small-signal stability analysis

各微源接入微电网的原理如图2所示，分别通过线路阻抗接入到母线。

图2 微源接入微电网原理图Fig.2 Schematic diagram of microsource connecting to microgrid

由图2可知，各微源接口在同一旋转坐标系下的网络方程为：

1.2 微源坐标变换

将统一参考坐标轴选在PCC，并定义PCC的电压矢量方向为统一坐标轴的d轴方向[8]，如图3所示。

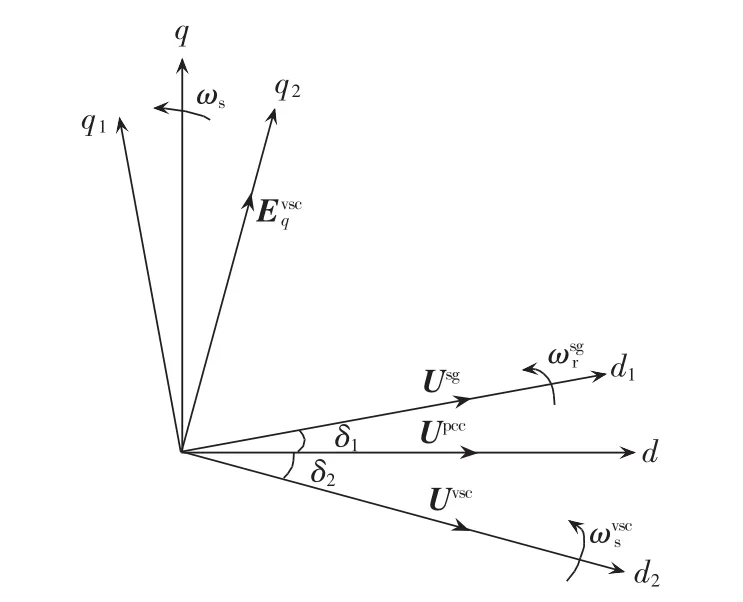
图3 本地坐标轴和统一坐标轴变换示意图Fig.3 Schematic diagram of transformation from local coordinates to unified rotational coordinates

同步发电机的本地坐标轴d1定向在其定子电压Usg上，以转子转速ωsgr旋转。VSC模型采用基于电网电压定向的方式，其本地坐标轴d2定向在VSC网侧电压矢量Uvsc上，以速度ωvscs旋转。

将DG1、DG2本地坐标系的各物理量变换到统一坐标系的变换方程为[6]：

其中，Fg=[FdFq]T为统一坐标系上变量的 d、q 轴分量；Fi=[FdiFqi]T为各微源本地坐标轴上变量的 d、q轴分量；变换阵Ti可表示为式（3）。

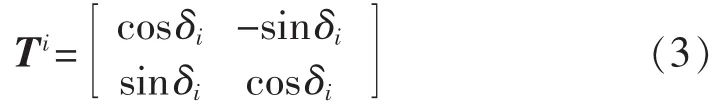
1.3 同步发电机小信号分析模型

进行微电网小信号干扰机电暂态分析时，忽略同步发电机定子绕组电磁暂态，只考虑转子运动方程、励磁控制器电磁暂态，得到同步发电机的微电网分析模型，用同步发电机五阶方程加一阶励磁控制器方程来表示[8]：

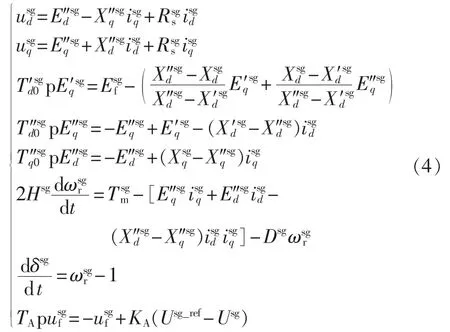
将式（4）在其本地坐标系线性化可将同步发电机的小信号分析模型表示成[7，9]：

1.4 VSC小信号分析模型

微电网中大量的微源如光伏发电、储能装置等都是通过VSC接入电网的。按照不同控制目标，VSC离网运行时的控制策略有U／f控制、PQ下垂控制和PV下垂控制等[10-12]。本文对PQ下垂控制和PV下垂控制进行对比分析，得到2种不同控制策略下VSC小信号稳定性模型。

1.4.1 PQ下垂控制小信号分析模型

当微电网离网运行时，PQ下垂控制算法采样VSC输出电压和频率，并根据下垂曲线计算出有功和无功功率参考值，下垂曲线方程表达为：

其中，P0、Pref和 Q0、Qref分别为有功和无功功率额定值、参考值；U0、U和f0、f分别为电压幅值和频率的额定值、实际值；kpf为P-f下垂曲线的斜率；kqu为Q-U下垂曲线的斜率。

PQ下垂控制框图如图4所示。

图4 PQ下垂控制框图Fig.4 Block diagram of PQ droop control

功率外环状态方程为：

其中，xp、xq分别为有功和无功PI控制器状态变量；Pvsc、Qvsc分别为VSC输出的有功和无功功率。

将方程（6）、（7）联立，并在本地坐标系线性化，得到VSC的小信号分析模型为：

1.4.2 PV 下垂控制小信号分析模型

基于电压调节的PV下垂控制如图5所示，控制VSC的无功功率可调节PCC的电压。当微电网离网运行时，PV下垂控制VSC输出频率和无功功率，并根据下垂曲线计算出有功功率和电压参考值。下垂曲线方程表达为：

其中，kpf、kuq分别为 P-f、U-Q 下垂曲线斜率。

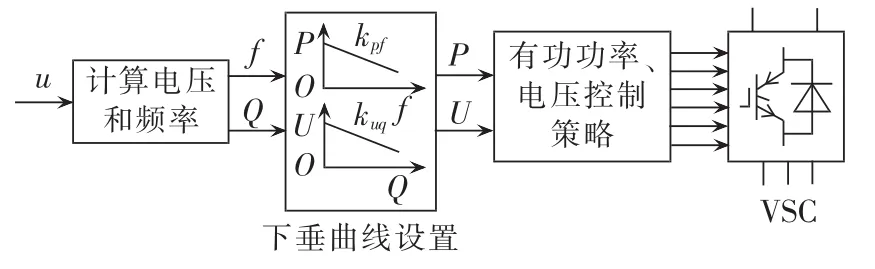
图5 PV下垂控制框图Fig.5 Block diagram of PV droop control

VSC的有功功率和电压外环控制方程为：

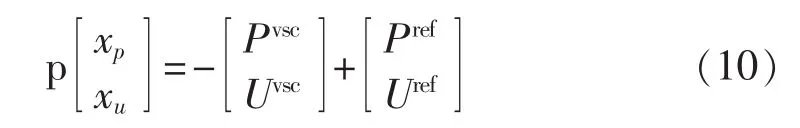
其中，xu为VSC电压外环控制器的状态变量。

将方程（9）、（10）联立，并在本地坐标系线性化，得到VSC小信号分析模型为：

其中，ΔXG2=[ΔxpΔxuΔωvscs]T为 VSC 的 PV 下垂控制状态变量；ΔuG2=[ΔPref2Δuref2]T为 PV 下垂控制的输入变量。

1.5 微电网系统小信号分析模型

本文主要针对微电网离网运行进行分析，微电网离网运行时负载方程为[13-15]：

其中，RL、XL分别为负载等效电阻和电抗；iloadd、iloadq分别为负载电流的d、q轴分量。

由网络结构可得微电网网络方程为：

将网络方程（1）和坐标变换方程（2）以及各微源小信号分析模型式（5）与（8）或（11）联立，消去 Δupcc，化简得到微电网的状态矩阵A和输入矩阵B为：

2 微电网仿真分析

仿真时，同步发电机线路阻抗R1+jX1=0.04+j 0.418 p.u.，VSC 线路阻抗 R2+jX2=0.212+j 0.527 p.u.，额定电压为 380 V／50 Hz。 VSC 的 Pref为 100 kW，Qref为 150 kvar。

2.1 逆变器PQ下垂控制

a.当同步发电机励磁调节器比例系数KA从0.1增至2时，主导特征根轨向左半平面移动，见图6。

图6 PQ控制下KA变化时微电网主导特征根轨迹Fig.6 Trace of system dominant eigenvalue vs.KAunder PQ control

当KA＜0.42时，采用PQ下垂控制的VSC无法保持稳定运行。

利用MATLAB／Simulink构建图1所示的离网运行模型，2 s时在负荷侧施加功率扰动，得到同步发电机输出的有功和无功功率随KA变化的响应，见图7。

当KA较小时，同步发电机输出功率无法维持稳定，输出功率振荡，仿真结果和特征根分析结果一致。这可以从物理上解释：当KA＜0.42时，同步发电机无法输出足够的无功功率维持输出电压恒定，导致微电网不稳定。

图7 PQ控制下 KA变化时的有功功率和无功功率时域仿真波形Fig.7 Time-domain simulative curves of active and reactive powers vs.KAunder PQ control

b.当同步发电机线路阻抗X1从0.0109 p.u.增大至0.7397 p.u.时，主导特征根向右半平面移动，当X1>0.6293p.u.时，主导特征根已位于右半平面，如图8所示，微电网失去稳定。

图9中，当X1较小时，同步发电机的有功功率和无功功率能够稳定输出；当X1>0.6923p.u.时，同步发电机输出的功率振荡。

图8 PQ控制下X1变化时的主导特征根轨迹Fig.8 Trace of system dominant eigenvalue vs.X1under PQ control

图9 X1变化时同步发电机输出有功和无功功率时域仿真图Fig.9 Time-domain simulative curves of active and reactive powers vs.X1

2.2 逆变器PV下垂控制

a.与PQ控制策略类似，KA从0.1增大至2时，主导特征根向左半平面移动，如图10所示。

图10 PV控制下KA变化时的主导特征根轨迹Fig.10 Trace of system dominant eigenvalue vs.KAunder PV control

当KA减小到0.1时，采用PV控制的微电网仍能维持稳定，而采用PQ控制的微电网此时已失去稳定。从图11可看出，在KA变化时，PV控制对微电网输出功率支撑作用优于PQ控制。

图11 PV控制下 KA变化时同步发电机输出的有功和无功功率的时域仿真图Fig.11 Time-domain simulative curves of active and reactive powers vs.KAunder PV control

b.同理，X1从 0.0109增大至 0.7397 p.u.时，主导特征根向右半平面移动，如图12所示。

图12 PV控制下X1变化时主导特征根轨迹Fig.12 Trace of system dominant eigenvalue vs.X1under PV control

当同步发电机X1增大到0.6293 p.u.时，采用PV控制的微电网能维持稳定，而采用PQ控制的微电网此时已失去稳定。从图13可看出，在X1变化时，PV控制对微电网功率支撑作用优于PQ控制。

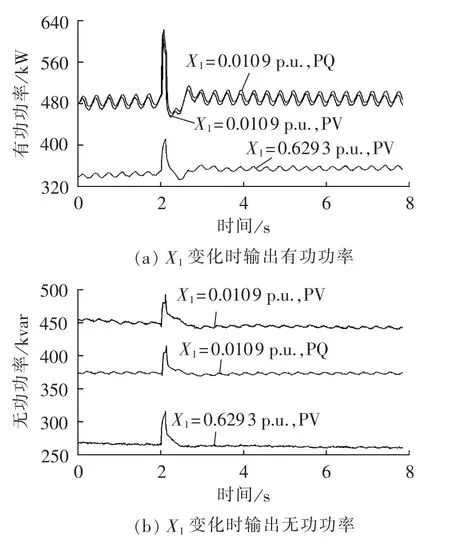
图13 PV控制下X1变化时同步机输出的有功和无功功率的时域仿真图Fig.13 Time-domain simulative curves of active and reactive powers vs.X1under PV control

3 结论

本文研究了含同步发电机和VSC典型接口的微电网小信号模型，分别建立了VSC的PQ下垂控制和PV下垂控制的小信号分析模型。分析不同控制策略下，控制器参数和网络参数变化对微电网稳定性的影响，得出微电网中VSC采用PV下垂控制时，稳定性优于PQ下垂控制的结论，在MATLAB／Simulink中验证了微电网模型建立和特征根分析的正确性。