基于多目标模块度的多层次电压控制分区方法

宋 越，程浩忠，张 健，邵 瑶，孙全才，李诗旸

（1.上海交通大学 电力传输与功率变换控制教育部重点实验室，上海 200240；2.中国电力科学研究院，北京 100192；3.爱荷华州立大学，美国 艾姆斯 50010）

0 引言

法国电力公司提出的三级电压控制模式[1]已在国内外得到广泛应用[2-5]，取得了良好的效果。该模式中，二级电压控制是协调本地控制和全局控制的中间环节，起到了承上启下的重要作用。作为二级电压控制的关键组成部分，电压控制分区受到了诸多学者的关注。电压控制分区问题属于NP（Nondeterministic Polynomial）难题，分区方法主要关注满意解的求取，常用的方法如聚类分析[1，6-8]和智能算法[9-11]等，其中聚类分析因物理意义直观明确而得到了广泛的应用和研究。

电气距离的定义和最优分区的筛选是聚类分析的关键。文献[1]提出了经典的电气距离定义，定义方式简洁、易于计算，在基于凝聚聚类[6]、分裂聚类（如 α 分解[12]）及模糊聚类[13]的分区方法中得到广泛应用，但该定义将所有节点设为PQ节点，没有突出无功源的控制特性；近年来，基于控制空间的电气距离定义[7-8]成为趋势。该定义相比文献[1]的定义更详细地刻画了无功源的电压控制特性，但涉及多维数据。而文献[14]指出，随着系统规模增大，聚类数据的维度增大，该定义对节点耦合程度的辨识能力会变差，导致聚类结果不准确甚至错误，即产生“高维聚类问题”。

最优分区筛选方面，目前多数研究[1，6-7]通过寻找聚类半径与分区数的关系曲线中的“平坦区”确定最优分区方案。该方法在物理意义上符合分区原则，但主观性过强，筛选的准确性受曲线形状的影响较大。部分研究引入了复杂网络理论[15]、证据融合理论[16]等方法评价分区质量，选取质量最高的方案为最优分区，取得了积极的成果，但评价角度不够全面，有待进一步研究。

针对上述问题，本文进行了以下几方面研究：提出了一种评价分区质量的多目标模块度指标，综合衡量方案的区域间解耦性和对故障的鲁棒性；提出了基于“化简-分区-还原调整”的多层次分区方法，其中化简阶段算法有效地处理了基于控制空间的电气距离定义在大系统中遇到的高维聚类问题。该方法的计算效率较高，并保证了区内连通性，避免了过多的人工调整。多个大中型算例结果验证了该方法的有效性和可行性。

1 无功电压控制特性分析

1.1 电压控制分区原则

电压控制分区目的是实现各区域电压控制的解耦。 根据目前研究[1，6，17]，分区应遵循以下原则。

a.中枢节点的代表性：区域中枢节点的电压特性能够反映区域内所有节点的电压特性。

b.区内可控性：区域内有足够的无功备用控制该区域电压。

c.区域间解耦性：区域电压由该区域无功源控制，受其他区域影响很小。

d.对故障的鲁棒性：故障前后，节点间的电气联系变化应较小；否则分区方案可能失去参考价值，该区域的控制优化措施也可能失效。该原则可看作区域间解耦性概念的扩充。

e.区内连通性：区域内部无孤立节点或被其他区域隔开。

f.变压器支路端点一致性：变压器支路两端节点属同一区域。

上述原则中，中枢节点可在得到分区方案后确定[1]，原则e和f将在算法中保证，因此聚类过程应重点满足原则b—d。以下分别对区内可控性和区域间解耦性进行详细分析。

1.2 区域内可控性分析：无功源节点电气距离

无功源（如发电机、SVC）节点对受控节点电压的控制能力可以通过准稳态电压控制灵敏度表征：

其中，ΔQG为无功源节点无功出力变化向量，ΔUL为受控节点电压变化向量；G为无功源节点集；L为受控节点集（包括无功出力已到达上限的无功源节点）；SLG为电压控制灵敏度阵，元素（SLG）ij表示无功源j的无功出力单位变化时受控节点i的电压变化量。为符合准稳态电压控制特性，通过逐次递归法[7]求解，即计算某个无功源节点的控制灵敏度时，其余无功源节点仍设为PV节点。

SLG各列SiLG为各无功源节点对受控节点的电压控制向量。由于电压控制的区域特性，在SiLG中，无功源节点i附近的受控节点对应分量较大，其余分量很小。若无功源节点i、j的电压控制向量相近，则表明二者的无功储备可共同用于控制其附近区域的电压水平，控制耦合度较高。因此可将无功源节点的电气距离定义为：

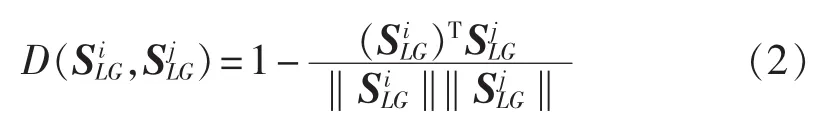
根据式（2），定义分区 s、t的电气距离：

其中，Gs、Gt分别为分区 s、t中的无功源节点集。 若分区s、t电气距离相近，表明分区s、t中无功源的控制作用相近，应在聚类过程中优先归并，以满足区内可控性原则。

1.3 区域间解耦性分析：模块度与最优方案筛选

聚类过程中产生了一系列的分区方案，应选取其中解耦性质最为合理的方案为最优分区方案。Newman等人提出了评价网络划分质量的模块度指标，加权网络的模块度定义为[18]：

其中，A为边权重矩阵，元素Aij为连接节点i、j的边权重；ΦP为分区方案；如果节点i、j属同一分区，则δ（i，j） =1，否则为所有与节点i相连的边权重之和，即节点i的度；为网络中所有边权重之和；为保持节点i、j的度不变而网络随机连接的情况下节点i、j之间边权重的期望值。分析式（4），若要增大M值，则需将权重大于期望值（即联系紧密）的支路两端节点划分至同一区域，权重小于期望值（即联系较弱）的支路两端节点划分至不同区域，显然这是一种合理的划分方式。因此M可用于评价分区质量。实践经验表明，M＞0.3时分区质量较高[18]。

本文将电网看作加权无向连通图，节点和支路分别为图的节点和边，提出2种模块度指标分别衡量分区方案的区域间解耦性和对故障的鲁棒性。

a.区域间解耦模块度M1。根据区域间解耦性原则，合理的分区方案应使区域内部支路两端节点的电气联系紧密，区域边界支路两端节点的电气联系较弱。为体现PV节点和PQ节点的不同特性，本文基于文献[9]的思想对电气距离定义进行改进，并定义M1。

其中，Ui、Qi分别为节点i电压和注入无功；dij为节点i、j的电气联系程度；yij为节点i、j之间的导纳值。若i为受控节点，αij定义为节点j电压单位变化时节点i电压变化量；若i为无功源节点，其电压不变化，αij定义为节点j无功单位变化时节点i无功出力变化量。节点 i、j的电气联系越紧密，αij越大，dij越小，（A1）ij越大。由前文对式（4）的分析可得，M1可以衡量分区方案的区域间解耦性。

b.故障鲁棒性模块度M2。根据分区方案对故障的鲁棒性原则，若支路两端节点的电气联系因支路故障而大幅减弱，则该支路应作为区域边界支路。由于逐一计算支路故障前后的电气联系变化耗时较多，可能出现潮流发散，故采用支路两端节点的电气联系对支路导纳的灵敏度表征支路开断前后支路端点的电气联系变化，并定义模块度M2。

式（7）中的偏导数可通过数值摄动法计算。由式（8）可知，支路鲁棒性越强，则 Δdij值越小，（A2）ij值越大。M2可以衡量分区方案对故障的鲁棒性。

分区方案质量由M1和M2共同表征，定义多目标模块度指标M∑：

其中，ΦPi为第i种分区方案。

M∑综合考虑了分区方案的区域间解耦性和对故障的鲁棒性，选择M∑最大值对应的方案为最优分区方案。

2 多层次电压控制分区方法

2.1 多层次分区思想

本文利用数据降维的思想[19]处理高维聚类问题。在电力系统中，一个节点通常与其附近的若干节点电气联系紧密，可看作一个节点簇。由于每一簇节点的电压特性可由其中枢节点的信息表征，若保留中枢节点的信息而略去其余节点的信息，可大幅降低电压控制向量的维度，从而提高聚类准确性和计算效率。据此本文提出了基于多目标模块度的多层次电压控制分区方法，如图1所示。多层次框架[20]分为以下3个阶段。

a.化简阶段：通过聚类找出节点簇，识别中枢节点，将系统原拓扑 G0=（VT0，E0）（VT0为图 G0节点集，E0为边集）逐步简化至 Gk=（Vk，Ek），电压控制向量维度降至设定水平。

b.分区阶段：基于简化后的系统，首先形成初始分区，再按各分区之间的电气联系逐步凝聚分区，并根据M∑选出最优方案。

c.还原调整阶段：将分区阶段得到的简化后系统分区方案还原为原系统方案，适当调整边界节点的区域归属，进一步优化分区质量，得到最终分区方案。

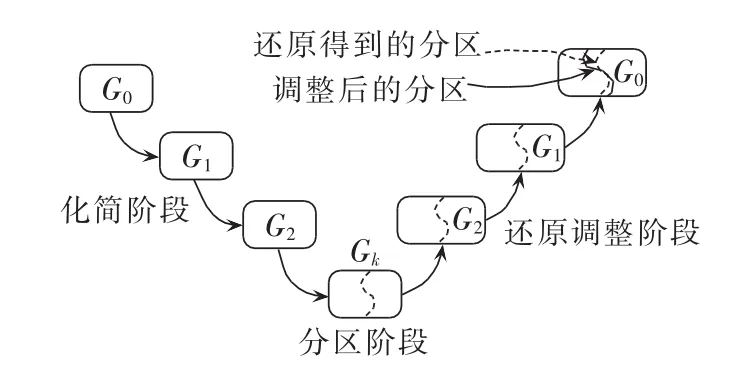
图1 多层次分区方法Fig.1 Multi-level network partitioning

2.2 电压控制分区步骤

2.2.1 化简阶段

a.节点初步聚类。

根据式（5）定义的dij作为节点相似度进行聚类，以快速找出电气联系紧密的节点簇。为保证聚类准确性，选取较底层（如聚类程度小于50%）的聚类结果。为不改变节点簇与外界的连通关系，选取聚合节点集中的连通子集作为节点簇。联络变压器两端的节点也作为节点簇，保证变压器两端节点分区一致性。

b.节点簇中枢节点选择。

对于节点簇Ck，根据簇中各节点间的电气联系，选择处于中心位置的受控节点作为中枢节点[1]：

若Ck中只有2个受控节点，则选取受控灵敏度较大的受控节点作为中枢节点：

c.简化电网拓扑与电压控制向量。

在保持节点簇与外部连通关系不变的情况下，将节点簇归并为一个节点，并将节点簇间的联络支路边权重的平均值作为归并后节点间的边权重。以图2为例，其中左图为原拓扑，图中虚线圈中为节点簇，右图为简化后的拓扑。若节点簇中含有无功源节点和受控节点，则将其等效为1个无功源节点和1个受控节点，二者相连，再与外部连接，如图3所示。此外为保证区内连通性，在分区阶段中规定二者属同一分区，发电机出口变压器两端的节点做相同处理。

图2 电网拓扑简化过程示意图Fig.2 Schematic diagram of network topology coarsening

图3 含无功源节点的节点簇简化示意图Fig.3 Schematic diagram of node cluster coarsening，including var sources

在电压控制向量中保留中枢节点对应维度，略去其余维度。若节点簇中无功源节点数大于1，则将这些无功源节点对应的电压控制向量叠加作为等效。

2.2.2 分区阶段

a.形成初始分区。

无功源的电压控制能力通常由近到远逐渐衰减，以各无功源节点为起点向周围扩展，可形成一系列小规模分区，作为初始分区。为保证区内连通性，本文按各节点的连通层次顺序分配区域编号，形成初始分区。以图4为例，图中节点1、2为无功源节点，其余为受控节点。节点1、2为第1层节点，区号分别为A、B。节点3—5与第1层节点直接相连，为第2层节点。节点5通过变压器与节点2相连，根据化简阶段的规定直接分配至B区。节点3、4则根据无功源1、2对其控制灵敏度的大小和连通情况分配区域归属。第3层和第4层节点的分配方法依此类推。所有节点分配完成后，若某分区只有孤立的无功源节点，则搜索其相连分区中的无功源节点，按式（3）计算距其最近者，归并到该分区。

图4 连通层次顺序说明Fig.4 Node connectivity levels

b.分区凝聚。

初始分区的离散程度较高，若对各区域间的解耦程度进行辨识，逐步归并电气距离相近的区域，可获得质量更高的分区方案。这一过程称为分区凝聚，具体步骤如下：若存在归并后对模块度有正贡献（即ΔM1＞0，ΔM2＞0）的连通区域，则按式（3）找出其中电气距离最近的一对区域（i，j）并归并；若不存在归并后对模块度有正贡献的连通区域，则归并连通区域中电气距离最近的一对。重复上述过程至所有区域归并为一个分区为止。

c.确定最优方案。

由式（9）计算初始分区与凝聚过程产生的各分区方案的多目标模块度M∑，取M∑最大者为最优分区方案。

2.2.3 还原调整阶段

设简化系统的分区方案中某节点属于分区A，而该节点由节点簇Ck归并而来，则将Ck中所有节点的分区号都设为A，由此可得到原系统的分区方案。由于该方案不一定是原系统的最优方案，在保证区内连通性的情况下，以最大化ΔM1+ΔM2为目标，调整该方案中区域边界受控节点的分区归属，得到最终分区方案。

分区算法总体流程如图5所示。算法的3个阶段相互配合、分工明确，计算效率较高。

3 算例分析

3.1 IEEE 118节点系统

对IEEE 118节点系统分区，分区方案与模块度的关系曲线如图6所示。多目标模块度M∑在分区数为7时取到最大值，对应分区方案如表1所示。以区域4和区域5为例分析该方案的合理性。发电机节点49（属于区域4）和发电机节点61（属于区域5）的端电压分别提高0.01 p.u.后区域4和区域5的受控节点电压变化情况（标幺值）如表2所示。可见发电机对本区域的电压控制效果明显，对其他区域的电压控制效果很小，可以忽略。因此该方案具有较强的区内可控性和区域间解耦性。

图5 多层次分区算法流程Fig.5 Flowchart of multi-level partitioning algorithm

图6 分区方案-多目标模块度曲线Fig.6 Curve of multi-objective modularity vs.sub-region quantity

对故障的鲁棒性方面，本文方案中的区域内部支路（开断后导致孤岛的支路除外）共有114条。逐一校验上述支路开断前后的分区方案，其中92%（105条）的支路开断后其两端节点仍属同一分区，这表明故障对区内节点电气联系的影响不大，分区方案对故障的鲁棒性较强。本文方案与文献中方案的对比如表3所示，本文方案的2种模块度指标值均最大，分区方案质量较高。

表1 IEEE 118节点系统分区方案Table 1 Partitioning scheme for IEEE 118-bus system

表2 实施电压控制后各区域节点电压变化Table 2 Bus voltage variations for different sub-regions with voltage control

表3 IEEE 118节点系统分区方案比较Table 3 Comparison of partitioning schemes for IEEE 118-bus system

3.2 大系统算例

以IEEE 2736sp系统为例考察本文方法处理高维聚类问题的有效性。在化简阶段设置不同的电压控制向量维度下降率进行分区。无功源节点的电气距离取值范围为0～1，考虑到电气距离较近（如取值为0～0.3）的节点归并可能性较大，为关键数据，故选取这部分数据进行分析，统计其方差和计算用时（在2GB内存、3.1GHz主频的计算机上运行得到，下文同）如图7所示。为便于比较，图中的数据已归一化，即为该点数值与维度下降率为0情况下的比值。由图7可见，电气距离方差随聚类数据维度的降低呈现变大趋势，这有利于数据辨识，同时计算用时随之减少。表4的分区方案质量对比也表明，化简阶段有效地处理了高维聚类问题，得到了质量更高的分区方案。

图7 IEEE 2736sp系统维度下降率-电气距离方差／计算用时曲线Fig.7 Curve of electrical distance variance／computational load rate vs.dimension reduction rate for IEEE 2736sp system

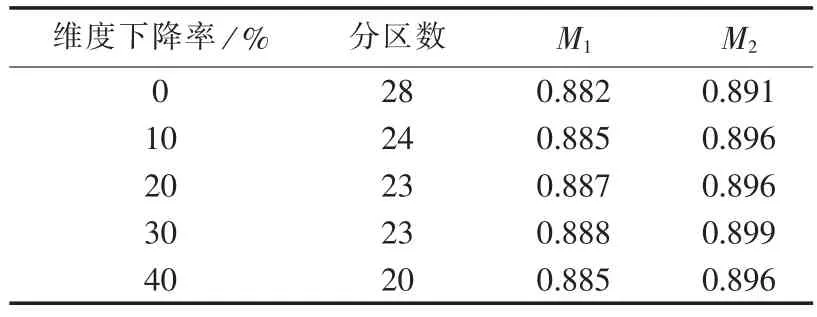
表4 IEEE 2736sp系统不同化简程度下分区质量Table 4 Partitioning quality of IEEE 2736sp system for different coarsening degrees

利用本文方法对若干大中型系统分区（电压控制向量维度均简化40%），分区方案与计算用时（聚类信息的计算时间未计入）如表5所示，可见本文方法在多个大系统中均得到了满意的分区方案。此外在大系统中，计算其电压控制灵敏度和模块度定义中的边权重矩阵的耗时较多，对于在线应用可以考虑预先离线算得这部分数据并在线调用的方法。

表5 若干大系统算例分区情况Table 5 Partitioning scheme for different large-scale systems

4 结论

本文研究了区域电压的可控性和解耦性，提出了无功源节点电气距离定义以及评价电压控制分区质量的多目标模块度指标，在此基础上利用多层次分区方法对系统进行分区。IEEE 118节点系统算例验证了本文方法的有效性，分区方案的区域内部联系紧密，区域间解耦程度较高，保证了区域内部连通性，符合分区原则。若干大系统算例测试表明，通过“化简-分区-还原调整”机制，多层次分区方法可以有效地处理高维聚类问题，降低问题规模，使算法以较高的计算效率得到高质量的分区方案，对于大系统电压控制分区和在线分区等问题有一定价值。