母线负荷异常数据复杂不确定性检测与基于综合云的修正模型

尹星露，肖先勇，孙晓璐

（四川大学 电气信息学院，四川 成都 610065）

0 引言

异常数据检测与修正是进行母线负荷预测的重要基础，已受到国内外重视［1］。导致母线负荷异常的原因很多，数据异常现象具有复杂不确定性，尤其是低压母线负荷的分散性进一步增加了复杂不确定性，异常数据检测困难。通常认为，改善测量、通信等硬件条件可提高数据可靠性［2］，但无法揭示母线负荷异常数据的固有规律，因此，研究母线负荷异常数据的检测与修正方法，仍是当前需要研究的重要课题。

国内外对异常数据检测与修正已开展了大量研究［1-10］。 文献［1，4］提出了基于变化率的判别方法，但对连续异常可能误判或漏判。文献［5-6］利用连续多日同时刻负荷的均值和方差进行检测，但对异常波动的检测效果不佳。文献［7］从负荷的横、纵向连续性出发，提出了基于数据密度的检测方法，但种子吸附阈值确定困难。对于异常数据修正，文献［1，7］提出了相似日同时刻负荷线性组合修正法；文献［8-10］提出了特征曲线调整法。这些方法遵循了负荷连续性原则，但对负荷变化的不确定性考虑不足。事实上，母线负荷变化同时具有连续性和不确定性，数据异常具有复杂不确定性，需针对复杂不确定性提出异常数据检测方法，并可用期望、熵、超熵等数学特征刻画母线负荷的复杂不确定性，采用李德毅院士提出的云模型进行修正。

本文基于聚类分析法，对母线负荷进行相似集划分；从母线负荷的纵向不确定性分布规律和横向连续性出发，研究异常数据的不确定特征，根据多日同时段负荷随机分布规律估算待测负荷在不同时刻的取值区间，检测异常数据，为避免疏漏，以相似日在不同时刻的负荷变化率的正常范围为判据，对剩余待测数据进行检测，从而提出异常数据复杂不确定性检测方法；研究母线负荷的期望、熵、超熵等数学特征，综合利用负荷准周期变化规律和当前趋势，提出基于综合云模型的修正方法，并对算法进行了详细研究。以某实际电网110 kV母线负荷为例，验证了方法的可行性和正确性，并将该方法用于某母线负荷预测系统，证明了其工程适用性。

1 母线负荷相似集划分

1.1 相似集概念与划分依据

合理的聚类可避免由于母线负荷的类别不同而带来的异常数据检测的误判、漏判等问题，也为异常数据修正奠定了良好基础。每15 min采样一次，以96个负荷点构成的日负荷曲线总样本集进行有效聚类，本文采用改进的模糊C均值FCM（Fuzzy C-Means）聚类方法［9-11］：利用减法聚类算法得到聚类数目和聚类中心，作为FCM算法的初始值，按最小距离原则对总样本进行划分，形成母线负荷不同类别的相似集。

1.2 相似集划分方法

a.设 N 天总样本集为 X=｛X1，X2，…，Xi，…，Xj，…，XN｝，Xi=（X（i，1），X（i，2），…，X（i，96）），计算各样本Xi的密度指标Di：

其中，ra为一正数，定义为样本Xi的一个邻域。

将式（1）中密度指标最高的样本Xi作为第一个初始聚类中心c1，对应的密度指标为

b.根据式（3）进行修正，从剩余样本中选取计算结果最大的样本作为下一个聚类中心。对应密度指标为

通常rb=1.5ra，可避免出现距离过近的聚类中心。

d.记g=1，将减法聚类得到的聚类中心c1（g）、c2（g）、…、ck（g）作为 FCM 算法的初始聚类中心。e.计算所有样本与各聚类中心的距离：

其中，μij为样本 Xi属于第 j类的隶属度，定义为式（5）。

其中，dij为样本Xi与第j类的距离；dil为样本Xi与每一类的距离；m一般取2。按最小距离原则将总样本X进行聚类。

f.重新计算聚类中心：

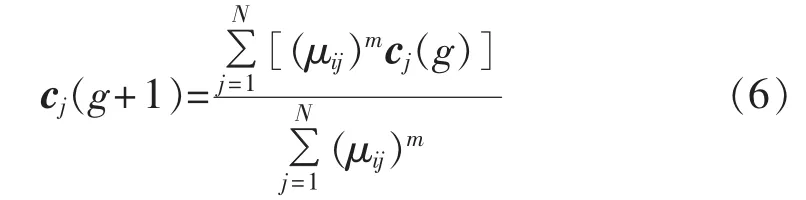
若存在 jє｛1，2，…，k｝，有 cj（g+1）≠cj（g），则 g=g+1，转至步骤e，否则聚类结束。最终形成母线负荷不同类别的聚类中心 c1、c2、…、ck和相似集 G1、G2、…、Gk。

2 异常数据复杂不确定性检测

2.1 异常数据检测基本思路

基于母线负荷纵向分布规律和横向连续性特点，提出异常数据复杂不确定性检测方法。基本思路为：按最小距离原则判别待测日曲线属于哪一个相似集，选取该相似集的n天样本作为待测日的相似日，并提取该相似集的聚类中心作为特征曲线。根据多日同时段负荷随机分布规律估算待测负荷在不同时刻的取值区间，检测得到r个异常数据，为避免疏漏，以相似日在不同时刻的负荷变化率的正常范围为判据，对剩余待测数据进行检测。

2.2 复杂不确定性刻画方法

根据D检验法［13］可证明多日同一时刻的负荷样本近似服从正态分布，以此为本文异常数据检测方法提供依据。假设检验问题为：H0样本服从正态分布，H1样本不服从正态分布。

检验统计量C（Y）为：

当 C（Y）>C（α，n）（可查统计量分布表［13］，α 为显著性水平）时，接受H0；反之，接受H1。由此刻画母线负荷的随机不确定性。

2.3 异常数据检测方法

按最小距离原则判别待测日曲线属于母线负荷哪一个相似集，选取该相似集的n天样本数据作为待测日的相似日，并提取该相似集的聚类中心作为特征曲线，算法如下。

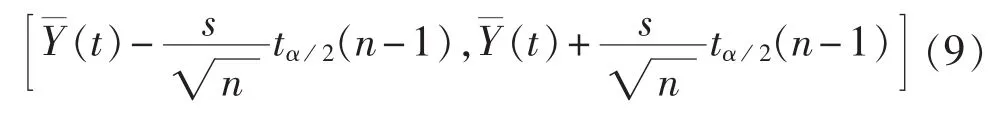
其中，s为标准方差；tα/2（n-1）可通过 t值表查询。

若Y0（t）不在对应时刻可能的取值区间，则判定该时刻的负荷为异常数据。步骤a—c基于母线负荷纵向分布规律，主要针对异常明显的缺失数据和极大、极小值进行检测，为避免其他异常数据疏漏，利用母线负荷横向连续性特点，对余下的96-r（r为步骤c已检测出的异常数据个数）个待测数据进行检测。

d.统计n天相似日在余下数据所对应时刻的负荷变化率的正常范围：

其中，i=1，2，…，n；t=2，…，96-r。

对于计算t=1时刻的负荷变化率时，可利用前一天最后一时刻的负荷值Y（i-1，96）进行负荷变化率运算。

e.计算待测负荷值Y0（t）与特征曲线所对应的Yc（t-1）的负荷变化率 δ（t）：

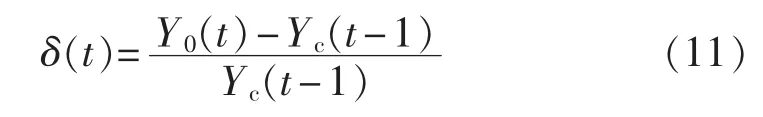
用 Yc（t-1）代替 Y0（t-1）的目的是避免 Y0（t-1）是异常数据而带来的误检。

f.判断 δ（t）是否在式（10）的正常范围，若不在，则说明该时刻的数据为异常数据。

3 母线负荷的数学特征与异常数据修正模型

3.1 母线负荷的数学特征

基于母线负荷变化的不确定性，本文采用云模型进行异常数据修正。云模型是用语言值表示某定性概念与其定量表示之间的不确定性转换模型。其数学特征为：期望Ex、熵En、超熵He。期望Ex刻画云的重心，熵En反映分布不确定性和可接受范围，超熵He刻画云滴的凝聚度，反映离散程度和云的厚度。

由D验证法确定多日同时段负荷的近似正态分布后，可利用普适性最强的正态云模型［14］刻画负荷变化规律，由此确定期望曲线方程：

3.2 异常数据修正的综合云模型

母线负荷曲线以96个负荷点为准周期，将n天相似日的负荷｛L（at，bt）｝（其中 at为时刻，bt为对应负荷）作为历史数据集DH，从整体反映负荷准周期性规律，依据DH中的数据可挖掘得到修正规则集｛A1如表1所示。 其中 Ai、Bi分别为at、bt论域上的定性概念，可由其数学特征（Ex，En，He）来表征。

表1 修正规则集Table 1 Set of correction rules

修正规则集中的Ai和Bi分别表示规则前件和后件语言变量的原子概念，通过判定待修正负荷的时刻at属于前件语言变量中的哪个原子来激活相应规则，令 μ=at，方法如下。

由参数 A1（Ex1，En1，He1）、…、Al（Exl、Enl、Hel）分别构造 μ- 条件下正态云发生器 CG1、CG2、…、CGl，将μ 分别输入云发生器得一系列输出 μ1、μ2、…、 μl，分别反映了μ对A1、A2、…、Al的隶属程度。从中找出最大值说明规则最能反映时刻 at的准周期规律，其后件 Bi相应（ExB，EnB，HeB）作为修正信息，可称为历史修正云Bi。历史修正云推理器的原理如图1所示。

图1 历史修正云推理器Fig.1 Reasoning engine of historic data correction cloud

以待修正数据的n天相似日同时刻at的负荷作为当前时刻数据集 DC，根据DC中的数据分布，用无需确定度信息的逆向云算法［16］得到当前时刻趋势——当前修正云Ii，该信息既有不确定性又遵循当前时刻数据的分布规律，其算法如下：

结合历史修正云Bi和当前修正云Ii，形成综合云修正模型 S（Ex，En，He）：

基于修正综合云模型S所得的修正数据L（at），同时包含了负荷整体特性和当前时刻数据分布规律，具体算法如下。

a.产生一个期望为En、方差为He的正态随机数E′n=NORM（En，He）。

b.以Ex为期望、E′n为方差得到一个正态随机修正数据 L（at）=NORM（Ex，E′n）。

c.检验所得修正值L（at）是否能满足横向连续性和纵向分布规律，计算公式如下：若不满足，转步骤b；若满足，将所得修正值L（at）作为最终的修正结果。

4 异常数据检测与修正算法流程

异常数据检测与修正流程如图2所示。

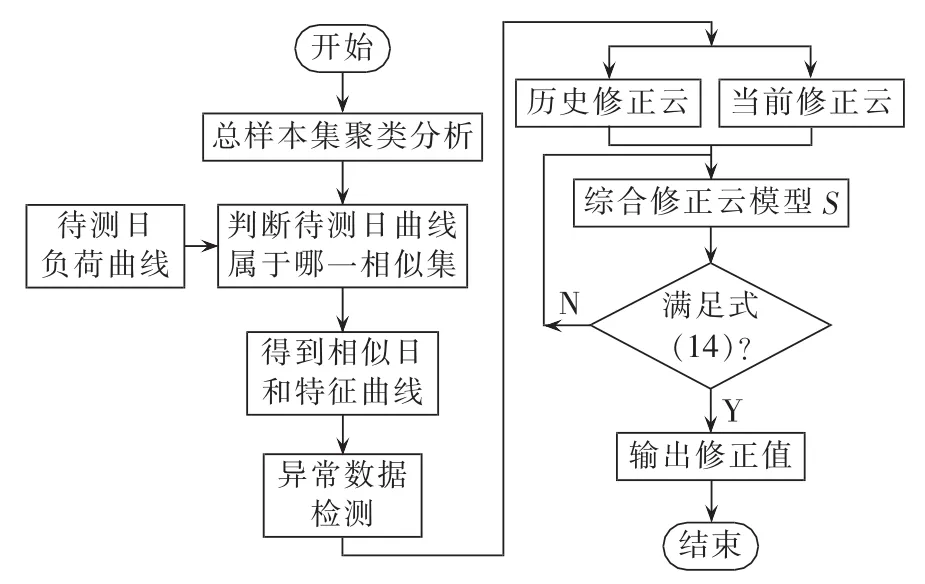
图2 异常数据检测与修正流程Fig.2 Flowchart of abnormal data detection and correction

5 实例分析

以某地区电网某110 kV母线为例，以2012年7月到9月的日负荷为数据源，人为丢失多个数据，并加入连续突变量。用本文方法进行异常数据检测与修正。上述算法均由MATLAB程序实现。

表2 为随机抽取负荷数据的检测结果，可见，本文方法的平均检测正确率为87.63%，高于改进横向法［1］的平均正确率 83.28%。

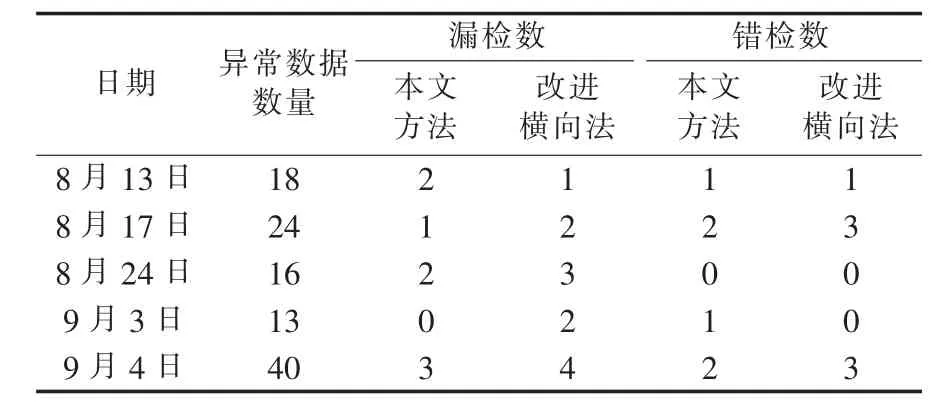
表2 随机抽取负荷数据的检测结果Table 2 Results of detection for randomly extracted load data

分别用加权平均法、特征曲线调整法［11］、综合云修正模型对异常数据进行修正。

加权平均法：选取待修正日的相似日的同一时刻的历史负荷数据作为参考数据，则修正值如式（15）所示。

其中，λj表征第d-j天t时刻负荷对待修正值的影响程度，本文取 λ1=λ2=…=λ5=0.2。

特征曲线调整法：若检测出t1到t2为坏数据，则修正值如式（16）所示。

其中，t=t1，t1+1，…，t2；Lc（d，t）、Lc（d，t1-1）、Lc（d，t2+1）为特征曲线上对应的负荷值；L（d，t1-1），L（d，t2+1）为待修正日曲线对应的负荷值。

以2012年9月3日的负荷曲线为例，修正结果和相对误差分别如表3、表4所示。

表3 异常负荷数据修正结果Table 3 Results of abnormal load data correction

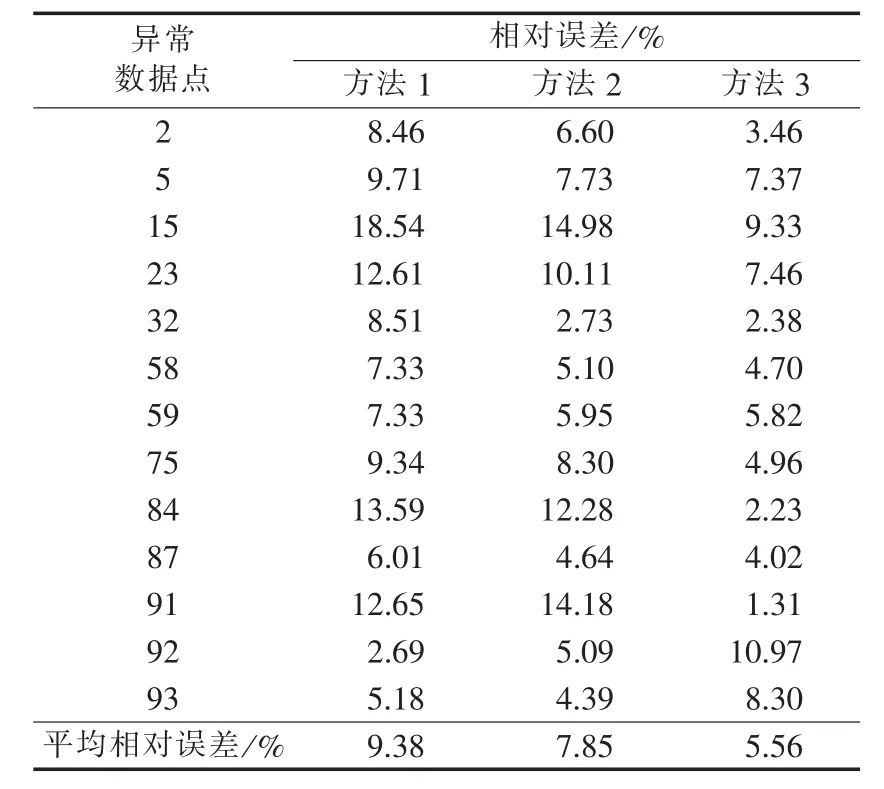
表4 各方法相对误差Table 4 Relative errors of different methods

从表3可知，本文方法所得修正值更接近实际。由表4可见，由于母线负荷的基数相对于系统负荷小，某些点相对误差偏大，用综合云模型修正后的相对误差基本在10%以内，平均相对误差比其他2种方法分别低3.82%和2.29%，明显好于其他方法。

为进一步比较，将以上3种修正方法处理后的样本和未经处理的样本用于某母线负荷预测系统，并以改进灰色模型预测法［18］为例，预测2012年9月10日到9月14日的负荷曲线。依据国网公司下达的《电网母线负荷预测工作考核管理办法》中的相关考核指标，母线负荷在t时刻的预测误差定义为：

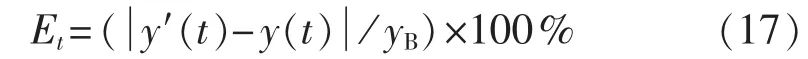
其中，y′（t）为实际值；y（t）为预测值；yB为负荷基准值，对应110 kV电压等级的yB=114 MW。日母线负荷预测准确率为：

如表5所示，用本文方法处理后的样本进行预测，平均预测准确率较其他2种方法处理后的平均准确率分别提高了0.23%和0.13%，较未处理时平均准确率提高了0.83%。

表5 母线负荷预测准确率对比Table 5 Comparison of bus load forecasting accuracy

6 结论

a.考虑母线负荷的纵向不确定性分布规律和横向连续性，采用异常数据复杂不确定性检测方法，其结果正确率高，可满足工程应用需要。

b.基于历史修正云和当前修正云的母线负荷异常数据综合云修正模型，同时考虑了不同时间粒度的变化规律，所得修正结果更符合实际。

c.本文方法在某地区电网母线负荷预测系统中的应用表明，采用本文方法后，母线负荷预测的准确率得到了明显提高，能更好地满足实际需要。

结合实际系统中母线负荷影响因素和变化规律，进一步考虑气象因素、计划检修、负荷计划性转移等的影响，是值得研究的课题。