贝叶斯网络法与盲数相结合的配电网可靠性评估

陈骥群，赵书强，马燕峰，胡永强

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

配电网可靠性评估常见的方法有故障模式后果分析法［1］、最小路法［2-3］、等值法［4］、混合型算法［5-7］等。此外还有新发展的人工智能算法如人工神经网络法［8-9］、模糊评估方法［10］等。但这些方法评估可靠性均是基于元件可靠性参数为确定值的假设，实际上天气的好坏、地理因素、统计资料的限制或者缺乏统计资料的新元件的投入等都会使元件的故障率、修复时间等具有不确定因素［11］。为了使评估结果真实反映出实际运行情况，应充分考虑参数的不确定性。考虑不确定性的一般方法是将可靠性参数作为区间数处理［12］，来评估负荷及系统的区间可靠性指标［13］。

贝叶斯网络［14］是20世纪80年代后期兴起的一种人工智能方法，利用推理模式将其应用到电网的可靠性评估中［15］，不仅能得到负荷及系统的可靠性指标，而且可以辨识出负荷及系统的薄弱环节，提出具有针对性的改进措施［16］。

基于贝叶斯网络法特有的双向推理模式，且计及元件可靠性参数的不确定性，本文将盲数［17-18］与贝叶斯网络相结合，应用贝叶斯网络建立含不确定因素的结构层次清晰的配电网模型。该方法全面考虑分支线保护、隔离开关、备用电源等的影响，综合考虑了配电网可靠性原始参数存在的随机性、模糊性、未确知性等众多不确定问题。建立系统的模型后，将元件参数的不确定性信息用盲数来表示，最终不仅得到系统的可靠性指标的范围及其对应可能性的分布情况，提供了比区间数更加全面的信息，而且定量给出了网络中特定部分对整个配电网可靠性的影响，识别出系统的薄弱环节。该方法可为工程技术人员提供更为丰富实用的信息。

1 模型建立

1.1 贝叶斯网络法简介

贝叶斯网络［14］是一种对概率关系的图解描述，它是一个有向无环图，其节点用随机变量标识，节点间的弧代表父节点与子节点之间的概率关系。已知一个系统的条件概率分布和网络的拓扑结构可得到系统的联合概率分布，应用贝叶斯网络推理的实质就是计算概率的过程。图1为一个简单的贝叶斯网络。

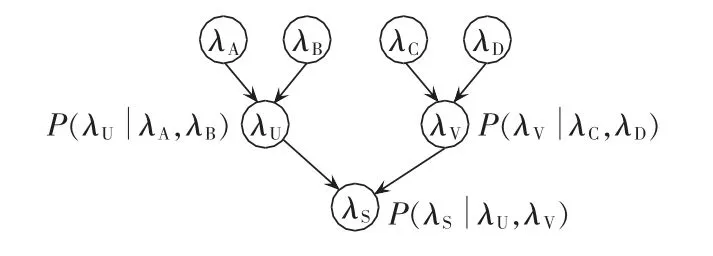
图1 简单贝叶斯网络Fig.1 Simple Bayesian network

假设图1表示一个可靠性系统，λA、λB、λC、λD是表征系统各元件状态的变量，λU、λV表征元件组合的状态，λS表征系统状态。状态量取“0”表示正常工作，取“1”表示故障。 根节点 λA、λB、λC与 λD分别具有先验概率分布 P（λA）、P（λB）、P（λC）、P（λD）。剩余节点具有条件概率表，例如 P（λU|λA，λB）表示节点 λU在父节点λA和λB下的条件概率［19］。图1表达了一个联合概率的分布：

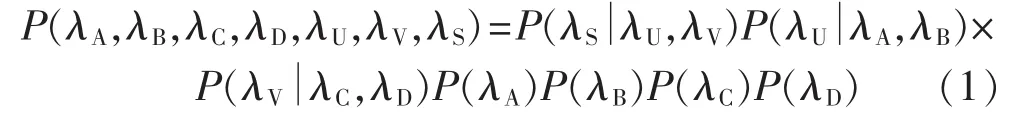
系统故障概率为：

若已知系统出现故障，则可根据已知的信息更新网络中其他节点的后验故障概率：即系统出现故障时，可后向推理出系统中的元件对该事件影响程度的大小，找出系统中影响此事件概率最大的即为系统的薄弱环节。

1.2 盲数模型

通过对原始数据的收集及对设备未来运行状况的预测得到影响配电网可靠性参数的因素（设备的故障率、修复时间等）集为 X＝ （x1，x2，…，xm），其中 xi（i=1，2，…，m）为可靠性参数的可能区间，本文采用自然断点法得到该区间。自然断点法就是将数据集中不连续的地方作为分级的依据，将数据集合进行分级。例如若需要处理p个数据，先将p个数据进行从小到大进行排序，区间中任意数据s1与sj需要满足sj-s1≤δ，其中δ为dj=sj-s1的平均值。以不满足约束的数据作为断点，从小到大依次化为m个区间，组成区间序列，即为可靠性参数的盲数的数值区间。

X为建立盲数模型提供了区间灰数值，该模型为m阶的盲数模型。为得到配网可靠性参数的盲数模型，还需xi对应的可信度αi。αi表示各个区间出现的可能程度，利用文献［20］中的判断矩阵法求得盲数对应的可信度。该方法首先要构造出指标因素集对可靠性的相对评价向量矩阵，然后两两比较评价因素得到判断矩阵，求解判断矩阵的最大特征根对应的特征向量，此特征向量即为所求盲数对应的可信度。

经过上述2步处理可得到盲数模型为：

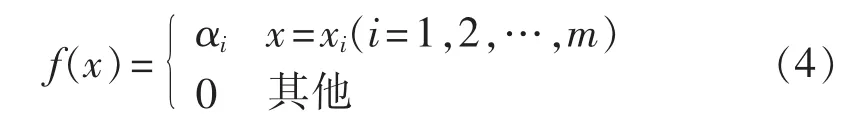
若某元件故障率出现在 x1=［a1，b1］，x2=［a2，b2］，x3=［a3，b3］，xi⊂X（i=1，2，3），3 个区间上可信度分别为0.1、0.6、0.3，则该元件故障率的盲数模型为：

可见盲数模型包含多种不确定性信息，可较全面地描述配电网可靠性评估中的不确定性信息，为评估具有不确定性信息的配电网可靠性奠定了基础。

2 贝叶斯网络与盲数相结合的配电网可靠性评估算法

将盲数与贝叶斯网络法相结合的配电网可靠性评估与传统贝叶斯网络评估方法相比，公式的形式相同，区别在于公式中的不确定性参数用盲数形式表示，用盲数运算代替实数运算。具体算法步骤如下。

a.根据不同时间、地区电力部门统计的资料及相关参考文献等，收集配电网可靠性原始数据。

b.建立配电网的盲数模型。通过对原始数据的收集及对设备未来运行状况的预测，得到设备的故障率为p个值；用自然断点法得到可靠性参数的盲数区间集；最后用判断矩阵法得到盲数区间对应的可信度。

c.结合贝叶斯网络法计算负荷点的可靠性指标。

对于组成配电网的元件节点，因其无父节点，它们的条件概率就是其先验概率。对于线路元件，其正常工作的概率为：对于变压器、断路器、负荷开关元件，其正常的工作概率为：

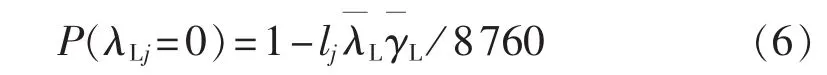
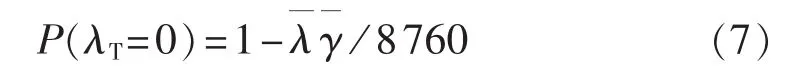
其中，lj为线路 j的长度为元件的故障率为元件的故障修复时间。本文均用形如的形式表示盲数。

负荷点i的停运概率PLPi为：

在实际运算过程中，为避免运算阶数增长过快，每次仅处理2个盲数，并对得到的结果按区间降阶［21］，例如2个3阶盲数进行运算会得到1个9阶盲数，而这个9阶盲数的取值会有交叉的现象，首先要除去交叉，即将交叉的部分分裂为新阶，对应的可信度也以同样的方式进行分配处理，然后根据所需要的阶数重新进行数据分配，降阶后再进行下一次运算。用该方法进行计算，计算量仅为点值贝叶斯网络的常数倍，该常数仅依赖于盲数的阶数。只要合理控制盲数的阶数，计算量并不是很大，得出的结果更具参考价值。

d.计算盲数形式的配电网可靠性评估指标，各个指标的贝叶斯网络形式的表达式如下。

系统平均停电频率（SAIFI，单位次/（用电用户·a））：

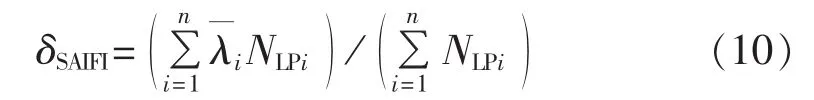
系统平均停电持续时间（SAIDI，单位h/（用电用户·a））：

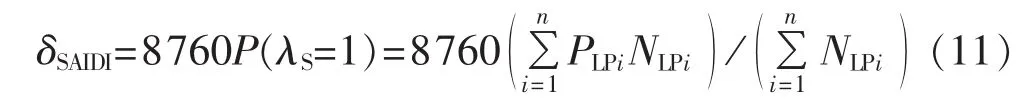
用户平均停电持续时间（CAIDI，单位h/（断电用户·a））：

平均供电可用度（ASAI，单位%）：

系统总电量不足指标（ENS，单位 MW·h/a）：

其中，ALPi为负荷点i的平均负荷；n为系统中负荷点的个数；NLPi为负荷点 i的用户数；P（λS=1）为系统出现故障的概率。

e.用贝叶斯的后向推理找到系统的薄弱环节，在系统故障已知的情况下，元件e0（其状态为λe0，其他类似）发生故障的概率为：

该概率取决于元件的可靠性参数，其故障率与修复时间的积最大的元件最可能是造成系统故障的元件，该元件就可能为负荷点的薄弱环节。

仅利用上述概率对负荷点进行薄弱环节分析难以识别整个配电网的薄弱环节，因为若元件的可靠性参数相同，因其在配电网中位置或周围开关的配置不同，其故障的影响也可能不同。所以用系统总电量不足指标来分析，根据分摊电量确定配电网薄弱环节，此方法更符合实际情况。第k个元件的分摊电量为：

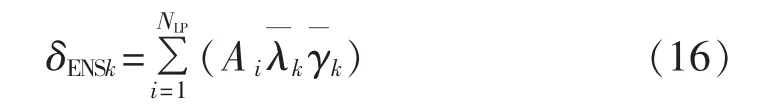
其中，Ai为负荷点i的负荷为第k个元件的故障率为第k个元件故障时负荷点i的缺电时间。

最后的评估结果可根据需要将盲数形式的可靠性指标转化为盲数期望值的形式，或直接取可信度较高的区间值的期望值作为可靠性指标进行参考。

3 算例分析

各种类型配电网均以单一的辐射型馈电系统运行。辐射型系统是由一组串联元件包括线路、隔离开关、分支线保护、变压器等组成。以某10 kV辐射型配电网为例，如图2所示，其中A、B、C、D为主干线路，a、b、c、d 为分支线路，考虑有隔离开关、分支线保护（r1—r4）及备用电源的影响的运行方式。

图2 辐射型配电网接线图Fig.2 Wiring diagram of radial distribution network

3.1 原始参数处理

设4个负荷点的用户数均为1，倒闸操作时间为0.5h，备用电源投入时间为1h，4台变压器参数相同，各主干线长度均为3 km，分支线长度1 km。由2006—2013年配电线路的故障率，将其转化为盲数形式。

表1 中数据经dj=sj-s1得到故障率差值，并取故障率差值的平均值作为断点处，可得δ=3.1，将此处作为断点，划分配电线路故障率盲数区间见表2。

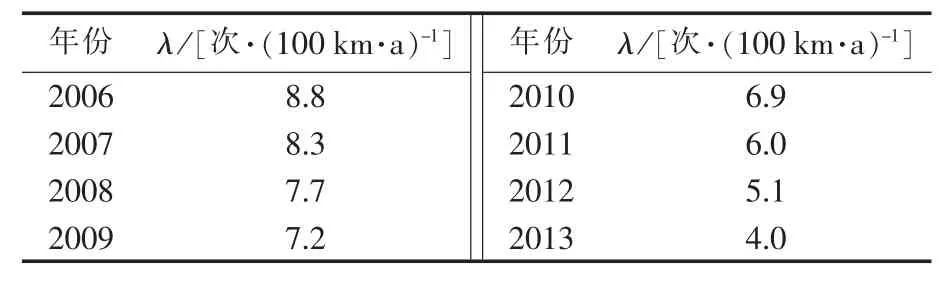
表1 配电网线路故障率Table 1 Line failure rate of distribution network

表2 配电线路故障率的盲数形式Table 2 Line failure rate of distribution network in blind number form

同理，通过对收集到的数据进行处理、分析，可得到各电气设备可靠性参数的可能区间，并用判断矩阵法得到各区间的可信度，进而得到参数的盲数模型。近几年的修复时间变化范围并不是很大，为减少计算，可以直接取最大最小值组成盲数的区间，对应的可信度为1。根据近8 a提供的配电网元件可靠性参数，用上述方法对其进行处理，结果如表3所示。

表3 中压配电网各种元件可靠性参数Table 3 Reliability parameters of different elements in medium-voltage distribution network

3.2 计算负荷点及系统的可靠性指标

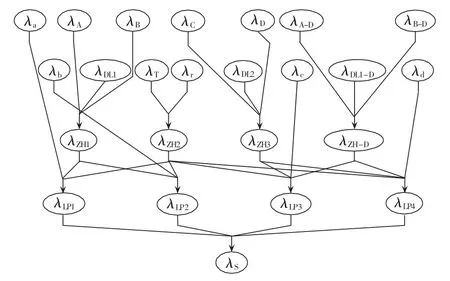
图3 配电网完整贝叶斯网络Fig.3 Complete Bayesian network of distribution network

建立贝叶斯网络模型如图3所示，图中λr为图2中分支线保护状态；λA-D、λB-D、λDL1-D为计及备用电源时，与备用电源有关的节点状态；λZH1、λZH2、λZH3、λZH-D为元件的组合节点状态（为减少贝叶斯条件概率表而设置的中间节点状态）。

用本文提出的方法计算负荷点的停运概率及系统的可靠性指标。用等值法［4］的评估结果做对比，等值法采用的可靠性参数为统计值的平均值。评估结果如表4、表5所示。

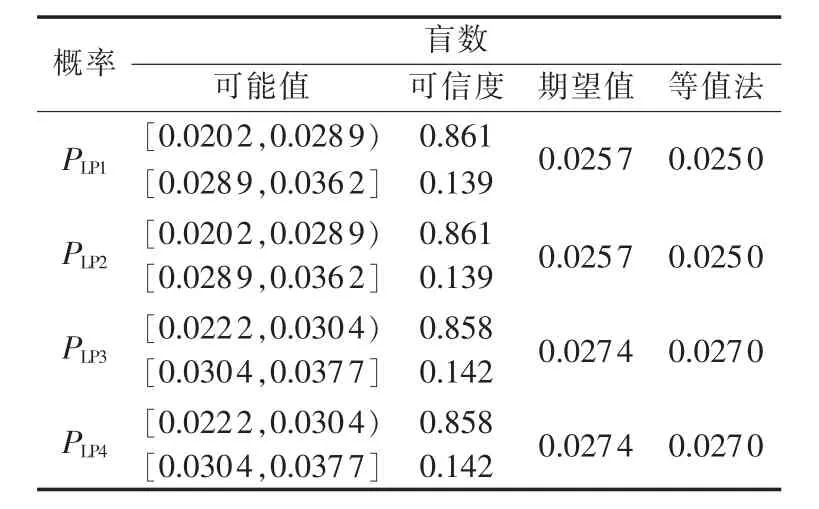
表4 负荷点的停运概率Table 4 Load node failure probability

表5 系统可靠性指标Table 5 Reliability indices of distribution network

通过表4、表5的结果可知，等值法的点值均落在了可信度较高的区间内，即盲数包含了点值方法计算的结果。盲数的期望值反映的是评估指标的整体期望，侧重于整体性，而传统方法得到的结果仅反映出该指标其中的一种情况。通过对比可以看出，传统方法评估结果没有反映出原始参数的不确定性对可靠性评估结果的影响，而运用本文提出的方法反映出参数不确定性的影响，评估结果既有区间形式及其对应可信度，又有以期望值表示的点值结果。可见盲数形式更符合实际情况，包含更丰富的信息。

3.3 配电网薄弱环节的分析

假设LP1—LP4的负荷均值分别为 0.535 MW、0.535 MW、0.454 MW、0.400 MW。 根据式（16）计算δENSk，分摊电量最大者为系统最薄弱环节。

根据计算可知：线路A、B分摊的系统总电量不足指标最多，为配电网最薄弱的环节。增加系统薄弱环节的可靠性可以比较高效率地提高整个配电网的可靠性。在实际配电网中，可综合考虑系统及负荷点的薄弱环节、负荷点的重要程度等因素，采取更加经济有效的提高系统可靠性的措施。现给出系统最薄弱环节的盲数形式作为参考，如表6所示。

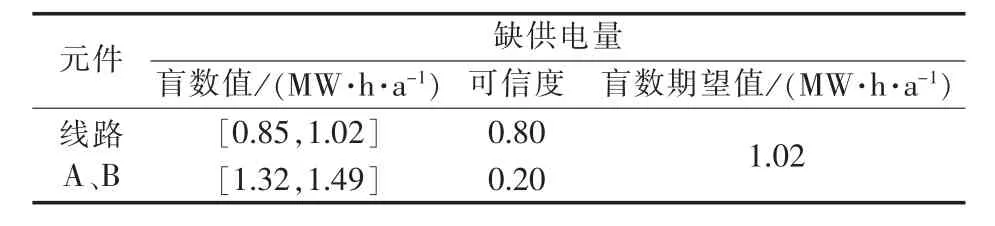
表6 系统的最薄弱环节Table 6 Weakest part of distribution network

4 结论

在配电网实际运行中，为尽可能考虑各类不确定因素对配电网可靠性原始参数的影响，本文将盲数与贝叶斯网络相结合，形成了一种新的可靠性评估方法。该方法计算出的可靠性指标包含了影响配电网可靠性评估的不确定性信息，并且描述出系统可靠性的真实程度（通常的灵敏度分析法、区间算法、模糊可靠性评估方法等均无法综合反映出这些信息）及辨识出系统的薄弱环节，为可靠性优化、电网规划等问题提供更加细致的数据，有利于做出最优决策，与实际情况结合紧密。通过算例验证了该方法的有效性。