基于负荷无功电压响应的切负荷控制决策优化

李 晔，张保会

（西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

电压稳定性、频率稳定性和功角稳定性是系统稳定性的3个主要方面，电压和频率作为衡量电能质量的重要指标，其稳定性已得到国内外的广泛关注［1-3］。然而，由于传统低频减载和低压减载装置还存在分散配置、缺乏信息交换、未考虑频率变化率等缺点，在严重故障下可能造成负荷的过切或者欠切。几起国际上的大停电事故也说明了传统的减载方案在保障极端故障情况下电力系统的电压稳定性和频率稳定性方面还存在着一些不足之处［4-5］。

目前，随着同步相量测量技术［6-7］在广域测量系统 WAMS（Wide-Area Measurement System）中的应用和不断发展，已有不少学者提出了综合考虑电压和频率响应的自适应减载方案。文献［8］基于WAMS，利用频率变化率获得系统有功缺额，并根据所提出的电压稳定性指标VQS进行切负荷量的分配。文献［9］将实际有功缺额与系统能承受的最大有功缺额进行比较，确定自适应减载方案的总切负荷量，并利用导纳矩阵和电压相量构建了电压稳定性判别指标L以确定切负荷地点和切负荷量。文献［10］提出暂态电压稳定性判别指标VSRI，并根据有功缺额的不同设计了2套自适应减载方案。文献［11］使用潮流追踪法，利用频率偏移量和电压稳定性判别指标VQS分别确定负荷的有功切除量和无功切除量，构建了综合考虑频率与电压响应的自适应减载方案。

然而，上述方案的切负荷量计算过程往往过于复杂，所需信息量大，对通信技术的要求较高。另外，上述方案没有充分计及感应电动机负荷对电压稳定性和频率稳定性的影响。通过文献［12-14］的分析可知，当系统发生严重故障时，感应电动机在负荷中所占比例越大，系统越可能发生负荷电压失稳以及频率过高等问题。因此，在充分计及感应电动机负荷特性，综合考虑系统频率与电压响应的基础上进行切负荷极有必要［15-16］。然而，如何得知节点负荷中感应电动机所占比例却是一个难题。

本文从感应电动机一阶等效模型出发，推导了计及负荷无功功率变化和电压偏移程度的切负荷量分配指标，该指标在物理意义上相当于负荷等效电纳变化量，指标大小不仅能衡量不同负荷模型对暂态电压稳定性的影响程度，同时还能反映感应电动机在该节点负荷中所占比例大小。本文利用该指标分配各节点的切负荷量，构建了综合考虑系统频率、负荷电压及无功响应的自适应减载方案。

1 切负荷量分配指标

电力系统的电压稳定性问题与发电、传输系统以及负荷特性有着密切联系，传输网络的强度和功率传输水平、发电系统无功和电压调节的限制、负荷和无功补偿设备的电压特性等共同决定着系统的电压稳定水平［5］。系统发生暂态电压失稳主要与系统传输能力受限和负荷特性的影响有关。目前，随着感应电动机动态负荷的日益增加，由负荷动态特性导致暂态电压失稳的可能性也随之加大［17-19］。本节将从感应电动机模型出发，推导由负荷无功和电压变化量构成的切负荷量分配指标，通过该指标来反映负荷特性对电压稳定性的影响。

图1为感应电动机一阶等效模型，图中，U为机端电压；Rs+jXs为定子阻抗；Rr/s+jXr为转子阻抗，s为感应电动机转差率；Xm为磁化电抗；P+jQ为感应电动机吸收的功率。

图1 感应电动机一阶等效模型Fig.1 Equivalent first-order model of induction motor

根据图1，忽略磁化电抗Xm，可得感应电动机所吸收无功功率的表达式为：

式（1）中转差率s对应的转子运动微分方程如下：

其中，H为惯性常数；Tm为机械转矩；Te为电磁转矩，其大小与U2成正比。

忽略式（2）中转差率s对机械转矩Tm和电磁转矩Te的影响，当感应电动机机端电压U下降时，电磁转矩Te将迅速减小，导致转差率s增大；根据式（1）可知，虽然无功Q随着U下降而减少，但s增大会造成电动机无功功率在扰动初期减少后又迅速增加［13］，加剧电压失稳过程。因此，转差率s的增加可以反映节点负荷暂态电压扰动大小和负荷稳定程度。然而，在实际系统中，负荷构成无法预测，感应电动机的转差率变化也难以获得。故将式（1）等号左右同除以U2得：

如式（3）所示，可通过测量 Q/U2的变化（可测量）来反映转差率s（不可测量）的变化，进而反映暂态电压稳定性和负荷稳定性。Q/U2从物理意义上看相当于感应电动机的等效电纳，本文即以等效电纳的变化量ΔQ/U2构成如下Y指标来进行切负荷量的分配：

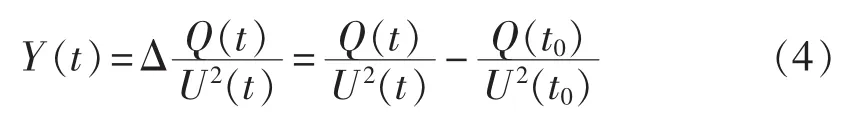
其中，Y（t）为扰动后t时刻的切负荷量分配指标大小；Q（t）和 Q（t0）分别为扰动后 t时刻以及扰动瞬间负荷吸收的无功功率；U（t）和 U（t0）分别为扰动后 t时刻以及扰动瞬间的负荷电压。Y指标与负荷吸收无功成正比，与负荷电压的平方成反比，在负荷无功需求增加或者电压跌落的情况下该指标将迅速增大，扰动后，节点的Y指标越大，则该节点的暂态电压稳定性越差。

对于感应电动机，将式（3）代入式（4）可得其Y指标为：

其中，s（t）和 s（t0）分别为扰动后 t时刻和扰动瞬间感应电动机的转差率。当s增大时，相应的Y指标也增大。

电力系统的负荷中除了感应电动机，还包括恒阻抗负荷、恒电流负荷以及恒功率负荷。由这3种负荷类型构成的节点负荷，其有功、无功功率可用式（6）和（7）所示多项式模型（ZIP模型）描述：

其中，AP、AQ分别为恒阻抗负荷在该节点的有功和无功负荷中所占比例；BP、BQ分别为恒电流负荷所占比例；CP、CQ分别为恒功率负荷所占比例；U0为负荷的额定电压；P0、Q0分别为负荷的额定有功功率和额定无功功率。将这3种负荷模型的无功表达式分别代入式（4）可得，恒阻抗负荷、恒电流负荷及恒功率负荷的Y指标分别如式（8）—（10）所示。

其中，RZ+jXZ为恒阻抗负荷的阻抗；Ic和sinφc分别为恒电流负荷的电流和阻抗角正弦大小；Qc为恒功率负荷的额定无功功率。

ZIP模型中，恒功率负荷对电压稳定性影响最严重，恒电流负荷次之，恒阻抗负荷对电压稳定性影响最小。当系统发生扰动时，恒功率负荷的Y指标与电压平方成反比，恒电流负荷的Y指标与电压的一次方成反比，恒阻抗负荷的Y指标始终为0。因此，对于恒阻抗负荷、恒电流负荷以及恒功率负荷，其对电压稳定性影响越大，发生扰动时相应的Y指标也升高越快。

将ZIP模型与感应电动机比较，由式（7）可知，对于ZIP模型，当电压跌落时，其无功功率不变或者减少，相应的Y指标增长较小；而对于感应电动机，由前述分析已知，其机端电压跌落时会造成转差率升高，使得负荷所吸收的无功功率增加，形成正反馈，从而进一步加快电压跌落，其Y指标增长迅速，在相同故障下感应电动机的Y指标将大于ZIP模型的Y指标。

综上所述，对于不同负荷模型（感应电动机、恒阻抗、恒电流、恒功率模型），Y指标大小差异明显。Y指标大小不仅能衡量不同负荷模型对暂态电压稳定性的影响程度，还能反映感应电动机在该节点负荷中所占比例大小。扰动后负荷节点的Y指标越大，则该节点的暂态电压稳定性越差，即该节点应切除更多的负荷。

2 基于负荷无功电压响应的切负荷控制决策优化

当系统出现严重扰动时，系统频率与负荷电压往往发生迅速跌落甚至崩溃，而传统减载方案仅根据本地信息进行切负荷，各减载装置间缺少信息交换，减载后可能无法保障系统稳定性。因此，设计一套综合考虑系统频率和负荷无功电压响应的自适应减载方案具有重要价值。本文基于切负荷量分配新指标，构建了如下自适应减载方案。

2.1 系统有功缺额计算

当系统频率与电压跌落时，通过WAMS将各发电机组的频率变化率传输到系统的控制中心，控制中心按照式（11）即可计算扰动发生瞬间全网的实际有功缺额：

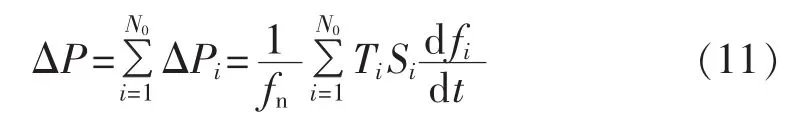
其中，i为各机组序号；N0为机组数量；ΔPi为第i台机组测得的有功缺额；Ti为第i台机组惯性时间常数；Si为第i台机组额定容量；fn为额定频率50 Hz；dfi/dt为第i台机组在扰动发生瞬间的频率变化率。

2.2 各节点切负荷量计算

系统需要切除的负荷量与全网有功缺额相等。若在全网进行切负荷，在获得了全网有功缺额之后，则可根据式（12）计算扰动后 0.5 s（即 t=0.5 s）时各节点负荷的Y指标大小。此处0.5 s的延时设置一方面是为了保证负荷的电压和无功功率在该段时间内有一定的变化量从而使得不同负荷节点的Y指标有较明显的差异，另一方面是为了与短路等故障造成的电压骤降相区别，不影响继电保护装置的动作。而后，根据式（13）将总切负荷量按一定比例分配到各个负荷节点。

其中，j为负荷节点序号；Yj（t）为扰动后 t时刻第 j个负荷节点的 Y 指标；Qj（t）和 Qj（t0）分别为扰动后 t时刻和扰动瞬间第j个负荷所吸收的无功功率；Uj（t）和Uj（t0）分别为扰动后t时刻和扰动瞬间第j个负荷的节点电压；ΔPj为第j个负荷节点的切负荷量；N为负荷节点总数可由 WAMS 实时获得。

然而，全网切负荷方案并未充分考虑各负荷母线电压失稳程度的差异，因此，本文利用式（14）作为切负荷地点选择判据，即将各负荷节点按照电压从小到大进行排序，并且仅选择母线电压不高于0.9 p.u.的负荷节点作为减载地点。

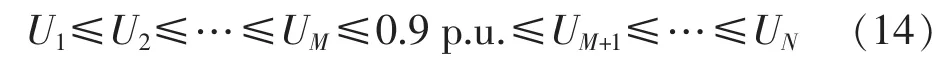
其中，M为母线电压不高于0.9 p.u.的负荷节点总数。这M个切负荷节点的切负荷量由式（15）计算得到：

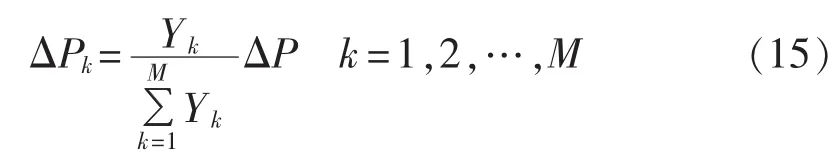
其中，k为各负荷节点序号；ΔPk为第k个负荷节点的切负荷量；Yk为第k个负荷节点在扰动后0.5 s的Y指标。

式（14）和（15）给出了切负荷地点选择和切负荷量计算的方法，即本文所提出的自适应减载方案。该方案选择电压跌落严重的节点进行负荷切除，并按照切负荷量分配指标（Y指标）的大小分配各节点的切负荷量，充分考虑了负荷电压的时空分布特性，能同时保障系统在严重故障下的暂态电压稳定性和频率稳定性。

3 算例仿真分析

3.1 失稳场景1

图2 为IEEE 39节点系统，系统各负荷节点所采用模型由感应电动机电磁暂态模型、恒阻抗模型、恒电流模型与恒功率模型并联构成，仿真在电力系统分析综合程序PSASP（Power System Analysis Software Package）上进行。失稳场景为31号机组在0.5 s时故障跳开，损失有功520 MW，并且6-11和4-14这2条输电线路同时跳闸。如图3所示（图中电压为标幺值），该扰动将造成大面积电压崩溃，并且由于电压快速跌落导致感应电动机发生堵转，负荷有功功率迅速减少，使得系统各机组频率升高至50.4 Hz，且振荡过程中最高机组频率超过50.6 Hz（如图4所示）。

图2 IEEE 39节点系统Fig.2 IEEE 39-bus system

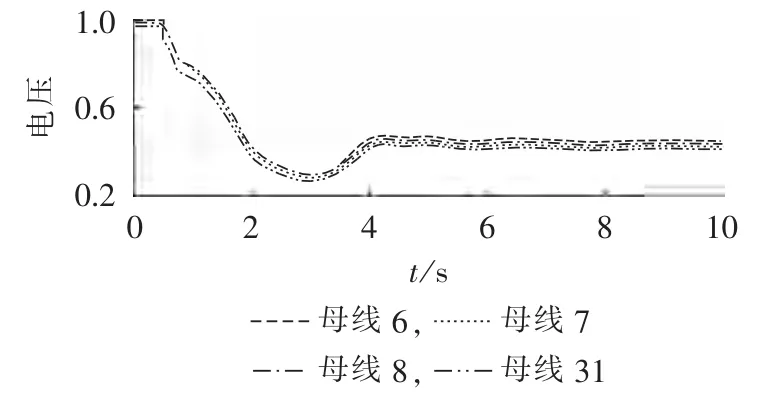
图3 负荷电压Fig.3 Load voltage

图4 发电机频率Fig.4 Generator frequency

3.2 Y指标分析

表1 为该失稳场景下故障后1 s时，母线8连接不同负荷模型时该节点负荷的电压偏移量（标幺值）、无功增量（标幺值）及相应的Y指标大小。

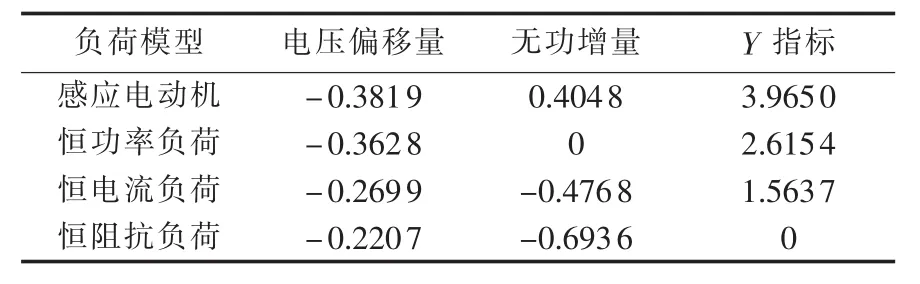
表1 不同负荷模型的Y指标对比Table 1 Comparison of index Y among different load models

如表1所示，对4种负荷模型进行比较可得如下结论。

a.恒阻抗负荷、恒电流负荷、恒功率负荷以及感应电动机负荷的电压偏移量绝对值依次增大，吸收的无功功率也依次增大，即不同负荷模型对电压稳定性的影响不同，感应电动机对电压稳定性影响最大，恒功率负荷次之，恒阻抗负荷对电压稳定性影响最小。

b.4种负荷模型的电压偏移量虽有差别但并不十分明显，而本文所提出的Y指标则可以明显区分出不同的负荷模型；从表1中可以看出，发生扰动时，感应电动机由于无功的增加，其对应的Y指标要明显高于恒功率负荷和恒电流负荷，而对电压稳定性影响最小的恒阻抗负荷，其对应Y指标在扰动过程中始终为0。

图5 故障后不同负荷模型的Y指标变化Fig.5 Variation of index Y after fault for different load models

图5 为表1所对应的不同负荷模型的Y指标变化曲线，易看出，故障后Y指标变化迅速，不同负荷模型的Y指标变化过程相差较大，Y指标大小不仅能反映不同负荷模型对电压失稳的影响程度，还能反映各节点负荷中感应电动机所占比例。因此，通过比较故障后各节点负荷Y指标大小则可快速筛选出对电压稳定性影响较大的负荷并对其进行控制。

3.3 减载效果对比

将本文的基于Y指标的自适应减载方案与按照负荷电压偏移量ΔU分配切负荷量的经典自适应减载方案进行比较。表2为4种减载方案的对比。表中，方案1为本文的自适应减载方案，即在负荷电压不高于0.9 p.u.的节点按照Y指标分配切负荷量；方案2在全网各节点按照Y指标分配切负荷量；方案3在负荷电压不高于0.9 p.u.的节点按照ΔU大小分配切负荷量；方案4为经典自适应减载方案，即在全网各负荷节点按照ΔU大小分配切负荷量；ΔUj为第j个负荷节点的母线电压偏移量。4种方案均在扰动发生后0.5 s进行切负荷。图6—8为4种减载方案的控制效果对比图（图中电压均为标幺值）。

表2 4种减载方案Table 2 Four load shedding schemes

由4种方案的对比结果可以看出，利用本文Y指标的切负荷方案（方案1和2），其减载结果要优于利用负荷电压偏移量ΔU的切负荷方案（方案3和4）；局部切负荷方案要优于全网切负荷方案（方案1优于方案2，方案3优于方案4）。

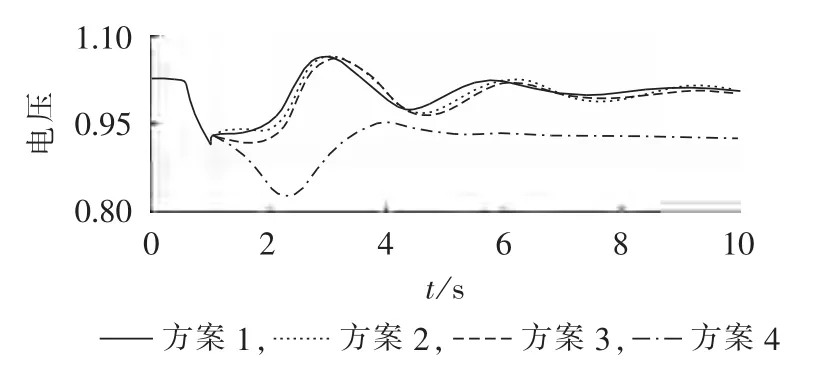
图6 减载后系统平均负荷电压Fig.6 Average load voltage after load shedding

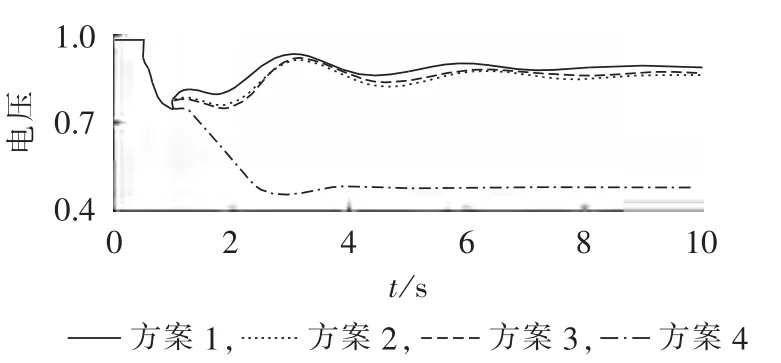
图7 减载后母线31电压Fig.7 Voltage of bus 31 after load shedding

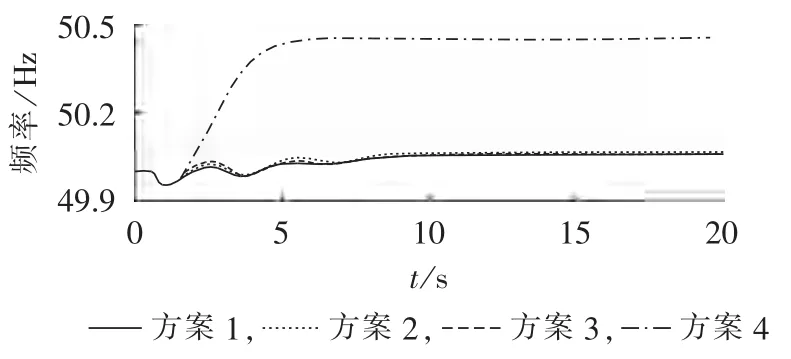
图8 减载后系统等效惯性中心频率Fig.8 Frequency of equivalent inertia center after load shedding

若采用方案4（经典控制方案），则减载后全网平均负荷电压比故障前下降约10%，而且局部地区仍会出现暂态电压失稳，其中负荷母线31的电压为全网最低电压，在故障后2 s内跌落至0.5 p.u.以下，另外，系统等效惯性中心频率将升高至50.45 Hz，超出了系统正常运行所能接受的频率最高值。

方案1、2、3均能保障系统的暂态电压稳定性和频率稳定性。其中，方案2（利用本文Y指标的全网切负荷方案）与方案3（利用ΔU的局部切负荷方案）效果相近，说明利用Y指标即使是在全网进行切负荷量分配，其减载效果也优于利用负荷电压偏移量在局部区域进行切负荷的方案，表明Y指标在反映负荷电压稳定性方面优于ΔU指标。

另外，方案1（本文的自适应减载方案）具有最佳的减载效果，减载后全网平均电压能够迅速恢复到1.0 p.u.，负荷母线31的电压即全网最低电压能迅速恢复至接近0.9 p.u.，并且系统等效惯性中心频率波动在±0.05 Hz范围内。

3.4 失稳场景2

失稳场景为39号发电机在0.5 s时故障跳闸，损失有功出力1 000 MW，该故障将导致发电机频率降低和全网大面积电压崩溃，而且由于电压的跌落使得频率在短时下降后迅速升高至50.5 Hz以上。采用如表2所示4种减载方案进行切负荷控制，本文的自适应减载方案仍具有最佳的减载效果，减载后全网平均电压能够迅速恢复到额定值，且频率偏移量最小。此处限于文章篇幅，故不再赘述。

4 结论

本文从感应电动机一阶等效模型出发，推导了计及负荷无功变化和电压偏移程度的切负荷量分配新指标，该指标从物理意义上看相当于负荷等效电纳变化量，在故障后该指标增长迅速，指标大小不仅能衡量不同负荷模型对暂态电压失稳的影响程度，同时还能反映该节点负荷中感应电动机所占比例大小。本文利用该指标分配各节点的切负荷量，构建了综合考虑系统频率、负荷电压和无功响应的自适应减载方案。相较于经典的自适应控制方案，本文所提出方案更能够有效地防止频率失稳和暂态电压崩溃，从而保障系统在大扰动下的频率稳定性和暂态电压稳定性。