多级检修模式下电网计划检修周期协调优化
赵 渊,张 煦,王 洁,范 飞,耿 莲
(重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
1 电力设备计划检修模型
电力设备故障率变化在整个寿命周期内呈浴盆曲线特性[1-2]。传统文献认为,电力设备在稳定运行期的故障率恒定,但实际上受零部件老化、磨损和隐藏故障等因素影响,故障率随时间呈升高趋势[3-4],进而导致系统风险不断攀升。计划检修是延缓设备劣化过程、降低故障检修成本、使系统恢复到一定可靠性水平的有效措施和重要手段。
就计划检修模型而言,通常假设设备经计划检修后以一定概率“修复如新”或“修复如旧”,两者的概率之和为1[5],对应检修方式分别称为完全检修和最小检修方式。但实际检修恢复效果与检修强度有关,往往介于“修复如新”和“修复如旧”之间,称该方式为不完全检修[6-7]。目前,基于不完全计划检修建模可分为3类:基于设备有效役龄模型[8],该模型便于快速计算检修后瞬时故障率函数值;基于故障率函数模型[9-10],该模型便于反映检修对故障率增长速率的影响;混合模型[11-12],该模型综合了上述2类模型的优点,因而被广泛应用于计划检修决策研究中。3 种模型如图1所示,其中 λ(k)(t)为第 k-1 至 k 次计划检修间的故障率函数,a(k)、b(k)分别为第 k 次计划检修对故障率和有效役龄影响因子,T为计划检修周期。
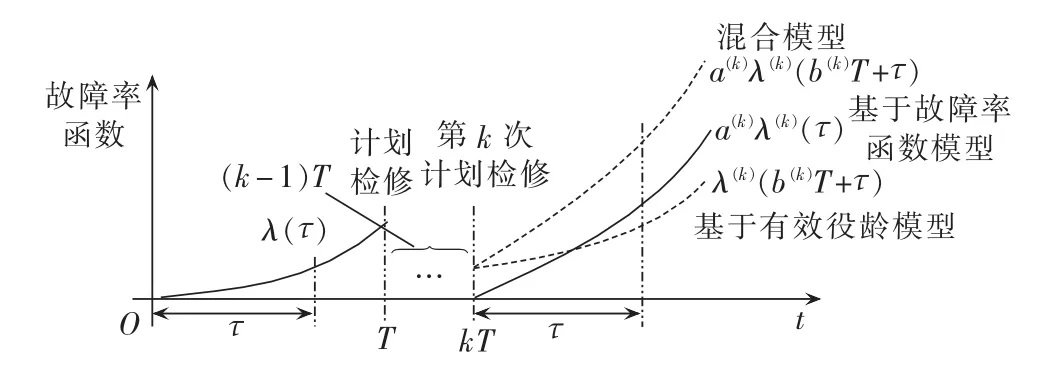
图1 不完全计划检修模型示意图Fig.1 Schematic diagram of imperfect preventive maintenance model
电力设备检修导则[13-15]将计划检修划分为A、B、C、D 4个等级,其中A级检修对设备进行全面解体检查和修理,检修最为彻底,但周期最长,一般为4~6 a;B级检修针对设备存在的问题,对其部分部件进行解体检查和修理,周期为2~3 a;C级检修根据设备的磨损、老化规律,有重点地对其进行检查、修理和少量零件的更换等,通常每年检修1次;D级检修是在设备总体运行良好的情况下,对其附属系统进行消缺检修。由于导则中各级检修周期相对固定,未考虑设备类型、容量、自身可靠性变化规律以及设备在电网拓扑中的位置等因素,极易导致“过检修”或“欠检修”现象。考虑到C级检修为目前电网进行的年度性常规检修,对系统可靠性影响显著,而A级检修最为全面和彻底,显著影响系统经济性,因此选取A、C 2个重要检修等级,并计入设备故障率变化规律及网络拓扑等因素,从系统层面开展多级检修模式下电网计划检修周期协调优化。
电力设备进行一定次数C级检修后会施行A级检修,设A/C级检修周期比率为N(整数),则电网A/C级计划检修周期优化问题变为包含C级检修周期和N的混合整数非线性规划(MINLP)问题。目前求解MINLP通常采用动态规划、遗传算法等方法,但这些方法均存在计算量大、效率低等问题。本文考虑到灵敏度指标能够反映连续型决策变量在给定值附近微小调整对决策目标的影响大小,而差分指标能够反映调节整数型决策变量对决策目标的影响程度,基于此,提出融合灵敏度和差分思想的电网多级计划检修协调优化启发式迭代算法。最后,针对RBTS和IEEE-RTS79系统开展A/C级计划检修协调优化研究,并探讨C级检修恢复因子变化对A/C级计划检修优化的影响规律。
2 计及多级检修的故障率模型
受老化、磨损等因素影响,电力设备故障率随时间呈升高趋势,部分文献对故障率增长效应进行了描述,如文献[2,16]采用阶梯函数,文献[17]采用指数分布函数,文献[18]采用威布尔函数来描述老化等因素对故障率的影响规律。本文采用β1=1的二重威布尔函数[19]描述电力设备随时间的增长效应,如式(1)所示,其中 αi≥0、βi≥0(i=1,2)为 i重威布尔分布的尺度参数和形状参数。
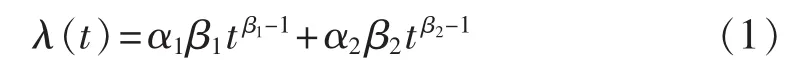
本文视C级检修为不完全检修方式,A级检修为使设备“恢复如新”的完全检修方式,事后检修为使设备“修复如旧”的最小检修方式,则A/C级计划检修下设备故障率曲线如图2所示。
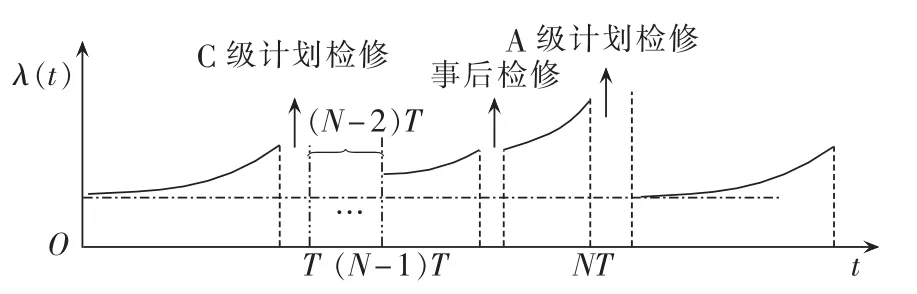
图2 A/C级计划检修方式下设备故障率曲线Fig.2 Curve of device failure rate in A/C-level preventive maintenance mode
假设电力设备A/C级检修周期比率为N,即每进行N-1次C级检修后进行1次A级检修。设电力设备C级检修周期为T,第i次C级检修前的有效役龄为y(i),第i-1至i次C级检修间的故障率函数为 λ(i)(t),故障率恢复因子为 a(i-1),役龄回退因子为 b(i-1),a(i-1)和 b(i-1)受设备 C 级检修次数等因素影响,随着检修次数的增大,改善效果逐渐变差,即:1=a(0)≤a(1)≤…≤a(N-1),0=b(0)≤b(1)≤…≤b(N-1)≤1。则有:
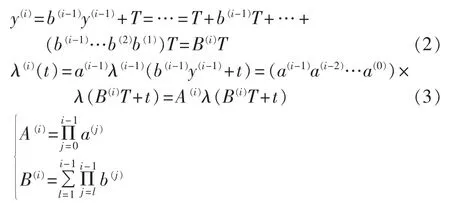
其中,i=1,2,…,N。
式(3)建立了元件故障率函数与C级检修周期和A/C级检修周期比率N的函数关系。
3 计及多级检修的系统可靠性、经济性指标
由第2节可知,元件每进行N-1次C级检修后进行1次A级检修,则元件A级检修周期内平均停运时间TD为:
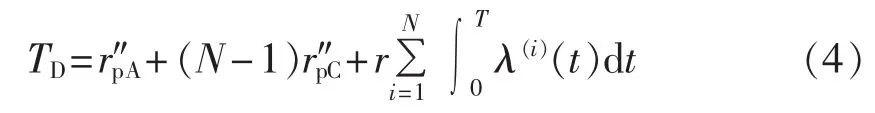
其中,r″pA为平均A级计划检修时间;r″pC为平均C级计划检修时间;r为平均事后检修时间。T、TD、r″pA、r″pC、r 的单位均为 h,λ(i)(t)单位为次 /h。
根据平均无效度概念,其定义为给定时间TT内平均不可用时间 TD与 TT的比值,结合式(2)、(3),可得元件平均无效度U为:
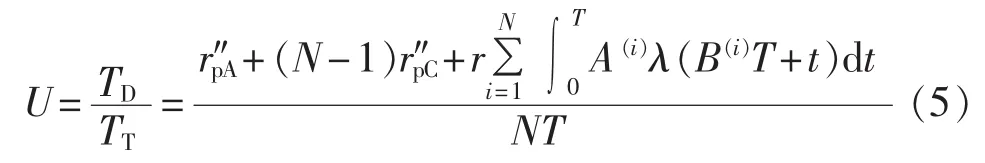
设M个元件组成的系统,元件状态相互独立,分别为 S1、S2、S3、…、SM,Sk=0 表示元件 k 处于正常状态,Sk=1表示其处于故障状态,则该系统状态x的概率可表示为:
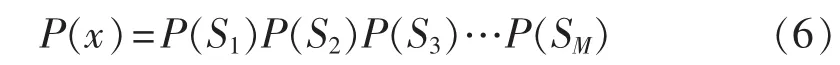
则多级检修模式下系统可靠性指标:系统失负荷概率δLOLP、电量不足期望δEENS的解析表达式分别如式(7)、(8)所示。

其中,Uk为元件k的平均无效度;X为系统状态集合;If(x)=0 表示系统正常状态,If(x)=1 表示系统故障状态;LC(x)为系统故障状态x下为使系统恢复到静态安全运行所需要的最小削负荷量。
系统总成本包括检修成本和停电成本,设单位停电成本为 CL(万元 /(MW·h)),则系统停电成本Closs可表示为:
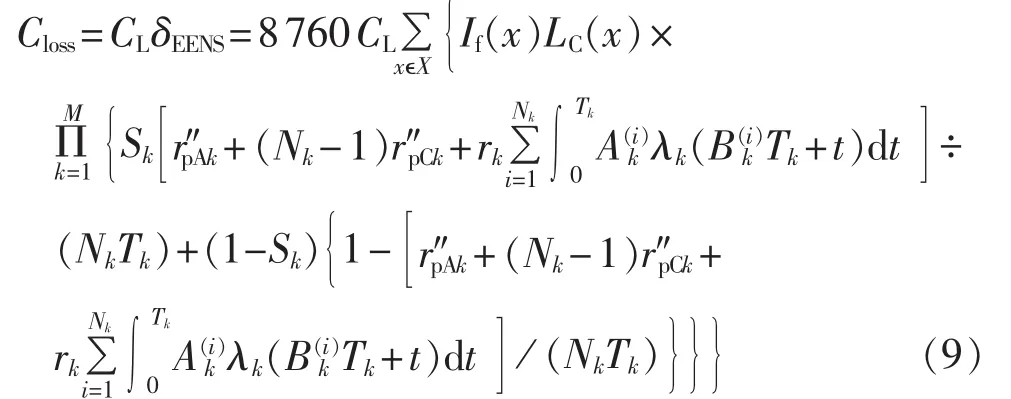
检修成本包括两部分,即检修材料费和施工费。设单位施工费为 CW(万元 /h);1 a 内元件 k(k=1,2,…,M)的期望事后检修次数为NCk,单次事后检修成本为CCk,其中事后检修材料费CCMk;A级检修次数为NpAk,单次A级检修成本为CpAk,其中A级检修材料费为CpAMk;C级检修次数为NpCk,单次C级检修成本为CpCk,C级检修材料费为CpCMk;单位停电成本为CL(万元 /(MW·h)),系统总成本为 Ctotal。 则有:
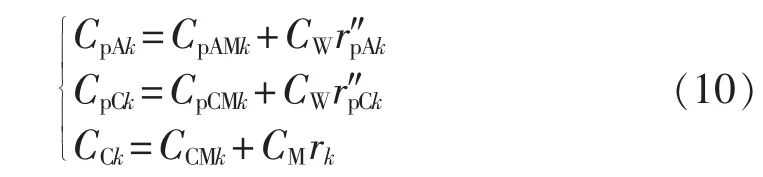
设备计划检修成本包括1次A级检修、N-1次C级检修,故系统A级检修成本、C级检修成本系统总检修成本Cplan表示为:
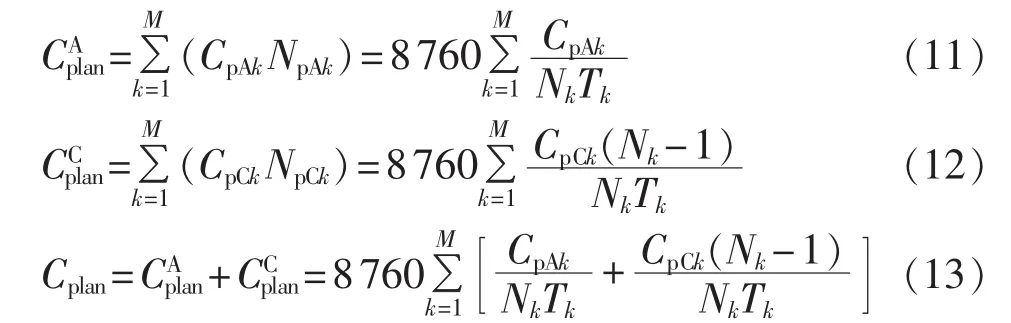
系统事后检修成本Ccor为:
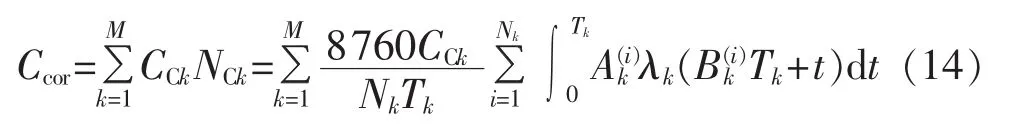
综上可得系统总成本Ctotal为:
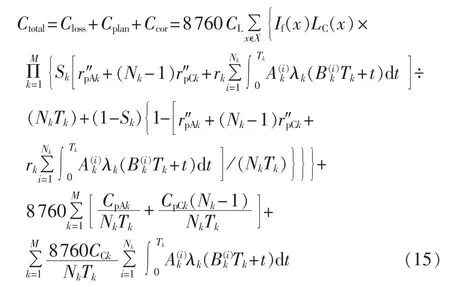
4 基于灵敏度和差分思想的电网多级计划检修优化启发式迭代算法
4.1 基本思想
鉴于灵敏度指标能够反映出连续型决策变量在给定值附近微小变化对决策目标的影响大小,而差分指标反映的是调整离散型决策变量对决策目标的影响程度,本文分别推导了系统总成本相对于C级计划检修周期的灵敏度公式和系统总成本相对于A/C级检修周期比率N的前向 /后向差分公式,以分别反映各元件C级计划检修周期调整、A/C级检修周期比率N调整对系统总成本的影响大小,从而指示2类决策变量的最优调整方向,最终寻求两者的协调优化。
设系统总成本相对于各元件C级计划检修周期灵敏度为 βse=(βse1,βse2,…,βseM),系统总成本相对于各元件A/C级检修周期比率N的前向差分ΔDe=(ΔDe1,ΔDe2,…,ΔDeM)和后向差分ΔDe=(ΔDe1,ΔDe2,…,ΔDeM)。其中灵敏度指标正值/负值最大分别表示缩短/延长对应元件C级计划检修周期对降低系统总成本最有效,从而确定了C级计划检修周期的最优调整方向。前向差分ΔDe、后向差分ΔDe分别反映的是各元件增大或降低A/C级检修周期比率N对系统总成本的影响。有以下几种情况:
① 当ΔDei>0、ΔDei>0时,表示增大元件i的A/C级检修周期比率Ni会增大系统总成本;
② 当ΔDei<0、ΔDei<0时,表示增大元件i的A/C级检修周期比率Ni会降低系统总成本;
③ 当ΔDei>0、ΔDei<0时,表示增大或降低元件i的A/C级检修周期比率Ni都会增大系统总成本,这种情况表明Ni是给定情形下元件i的最优A/C级检修周期比率;
④ 当ΔDei<0、ΔDei>0时,这种情况不存在,原因在于系统总成本是关于元件A/C级检修周期比率Ni的凹函数。
由于情况④不存在,情况③本身处于最优状态,因此只需考虑情况①和②下的A/C级检修周期比率调整方式。对于情况①,寻找中的最大值,降低对应元件A/C级检修周期比率对减小系统总成本最有效;对于情况②,寻找ΔDe中的最小值,增大对应元件A/C级检修周期比率对降低系统总成本最有效。
通过上述灵敏度和差分方式探寻C级计划检修周期和A/C级检修周期比率N的最优调整方向,能有效确保每次迭代过程的最优搜索方向,最终实现2类决策变量的快速协调优化,如图3所示。
4.2 计及多级检修的灵敏度公式
元件状态概率相对于其C级检修周期的灵敏度详细推导过程如下。
由于:
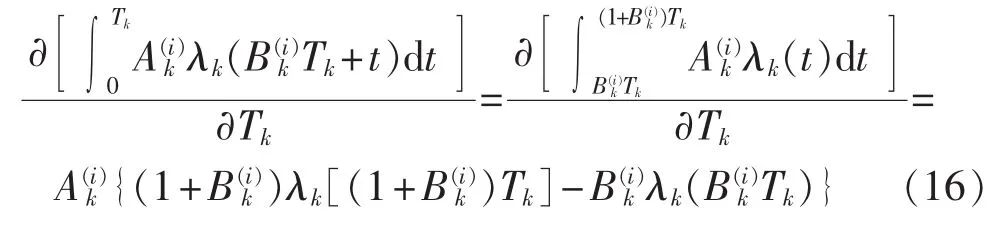
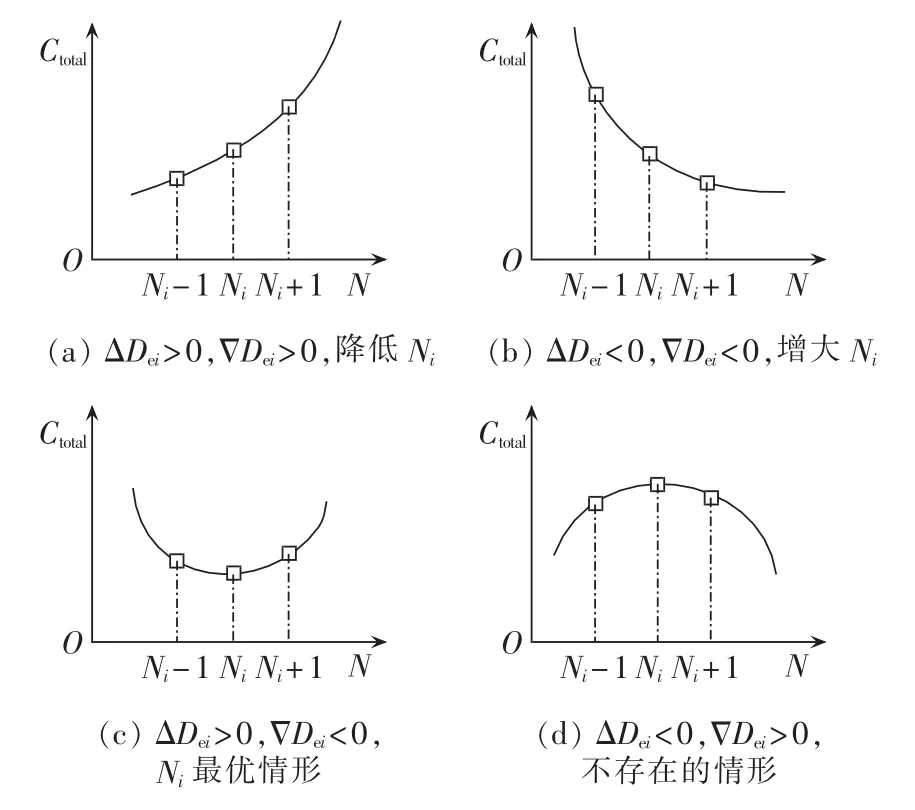
图3 各情形下A/C级检修周期比率的调整方向判别Fig.3 Adjustment direction of A/C-level maintenance cycle ratio for different situations
所以:
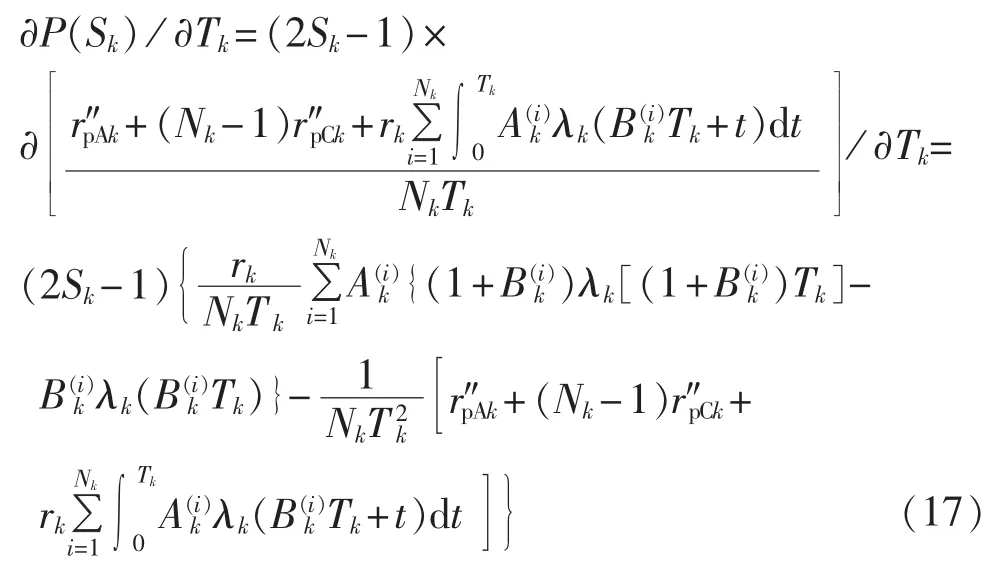
由于元件状态相互独立,则元件i的事后检修费用和计划检修费用只与元件i的计划检修周期有关,而与元件 j(i≠j)的计划检修周期无关,则可得式(18):
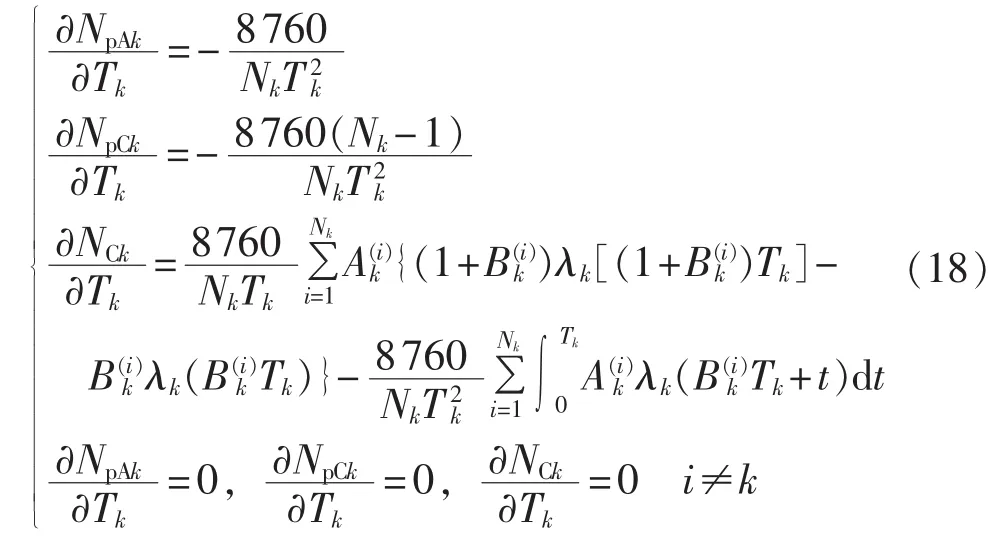
∂NCk/∂Tk的详细推导过程如下。
由于:
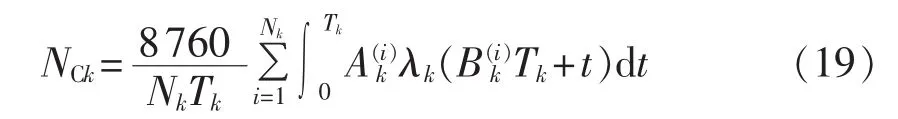
与式(16)推导过程相同,可得:
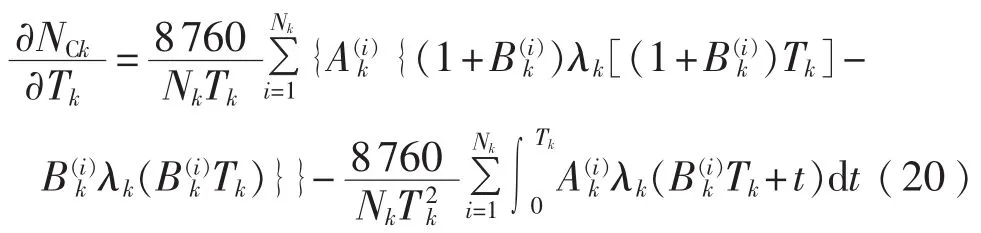
则系统停电成本对C级检修周期的灵敏度:
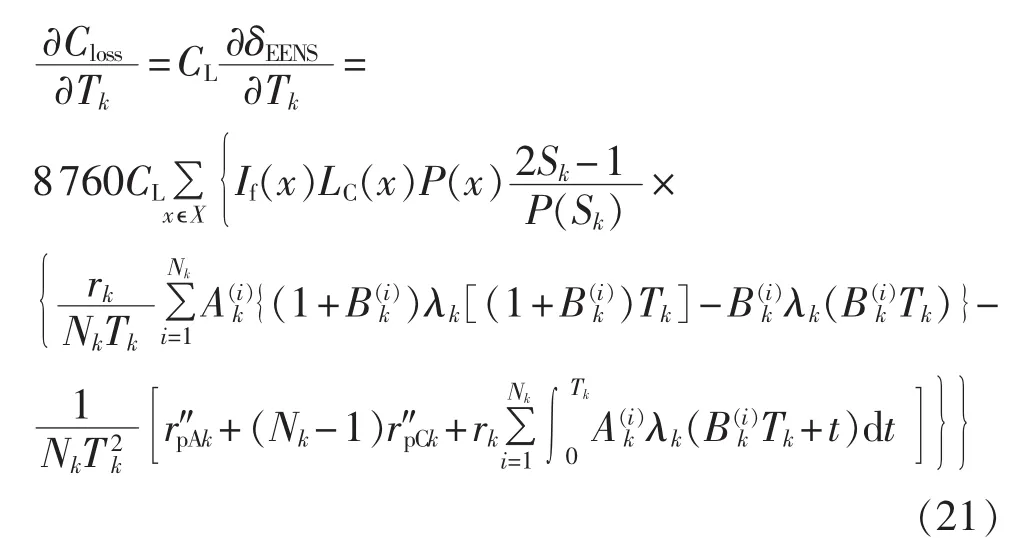
系统计划检修成本对C级检修周期的灵敏度:
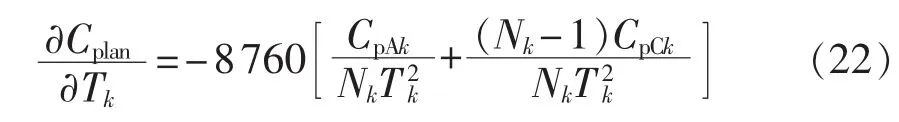
系统事后检修成本对C级检修周期灵敏度:
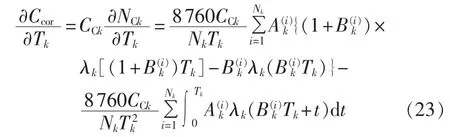
则系统总成本对C级检修周期的灵敏度:
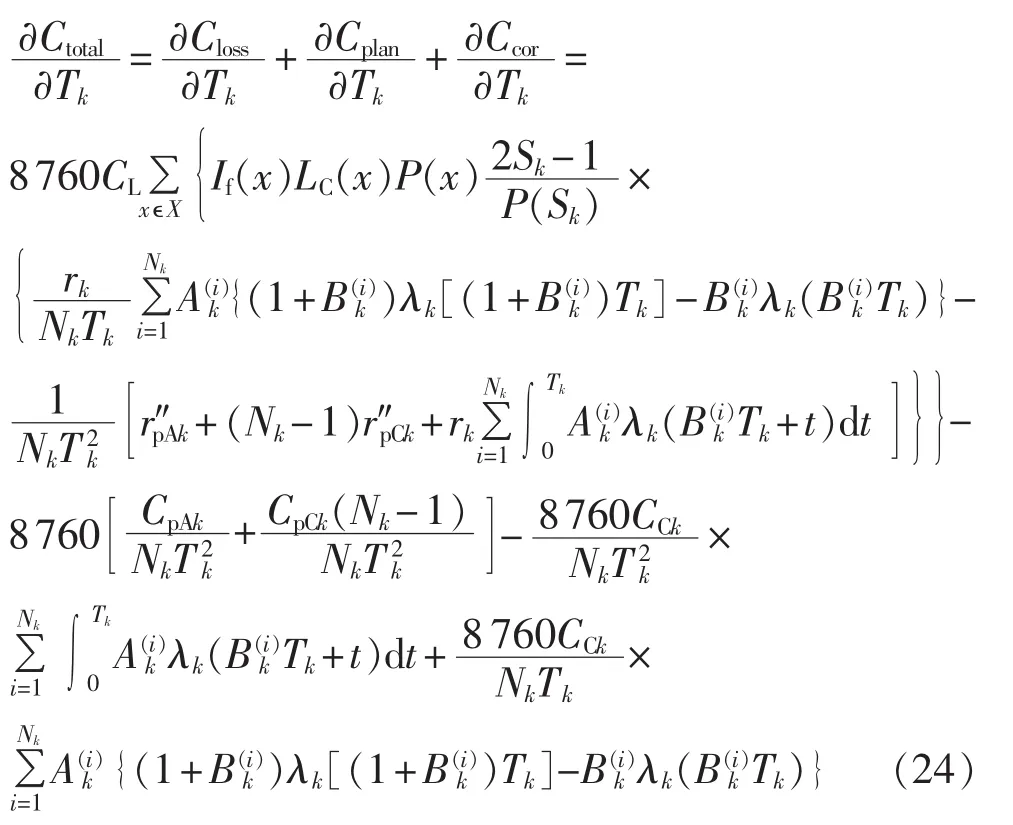
4.3 计及多级检修的差分公式
元件k状态概率P(Sk)相对于其A/C级检修周期比率Nk的前向差分、后向差分公式见式(25)、(26)。由此可推得停电成本Closs前向差分、后向差分公式如式(27)、(28)所示。
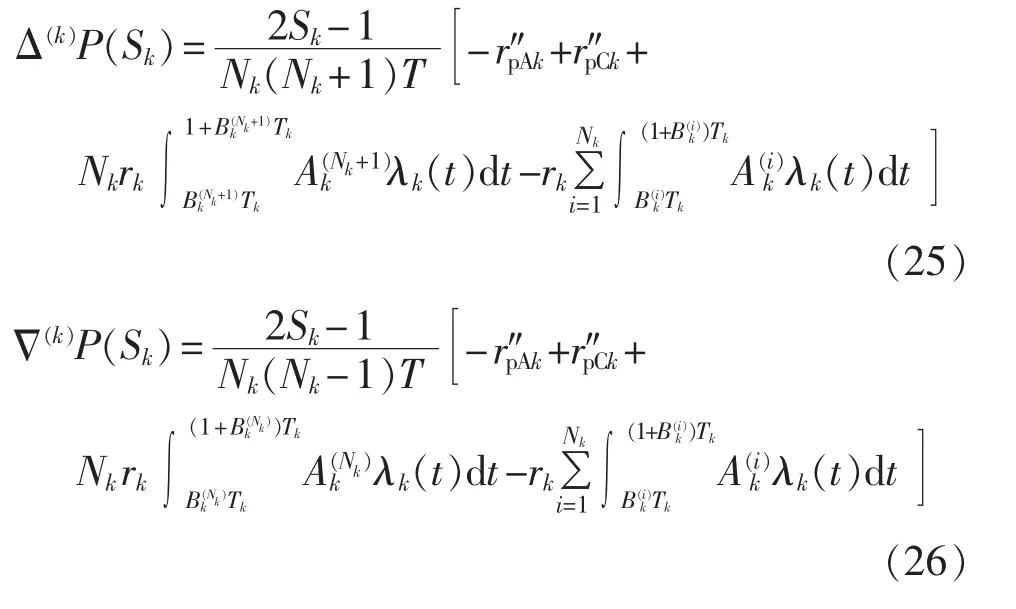
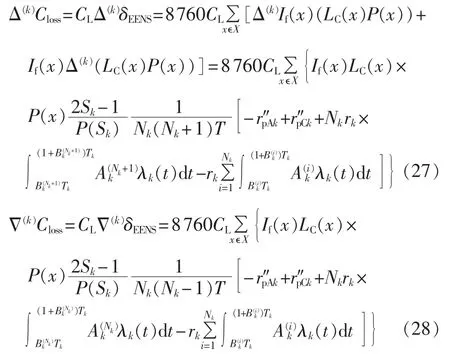
计划检修成本Cplan前向差分、后向差分公式:
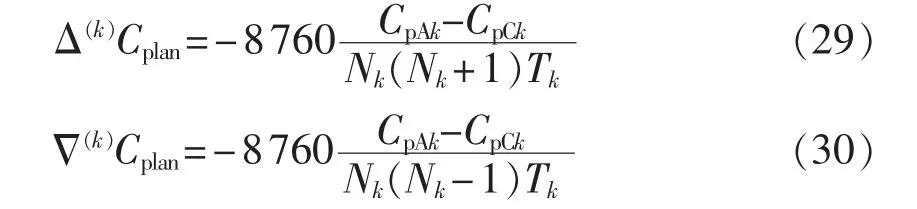
事后检修成本Ccor前向差分、后向差分公式:
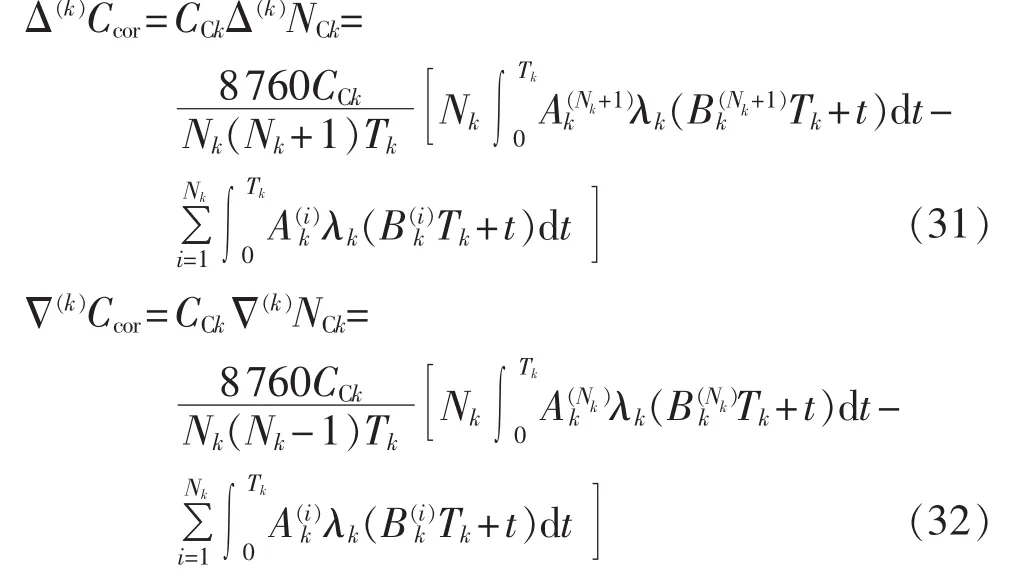
则系统总成本Ctotal前向差分、后向差分公式如式(33)、(34)所示。

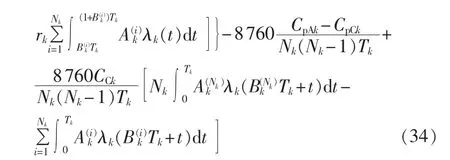
4.4 基于灵敏度和差分思想的电网多级计划检修优化启发式迭代算法
以系统停电损失和检修成本之和最小为目标,基于系统总成本相对于C级检修周期的灵敏度分析及系统总成本相对于A/C级检修周期比率N的前向差分和后向差分指标,对系统各设备的A/C级检修周期进行启发式协调优化。具体算法流程如下。
a.采用状态枚举法枚举电力系统故障状态,并基于直流潮流最优削负荷模型[20],计算各枚举状态下的系统最小削负荷量,若削负荷量大于0,则记录该系统状态及对应的削负荷量,最终得到一组系统故障状态(X1,X2,…,Xm)以及对应的削负荷量(Lc1,Lc2,…,Lcm),其中m为枚举到的故障状态数。
b.输入系统中各设备故障率模型参数和各设备修复时间、初始 C 级检修周期(T1,T2,…,TM)和 A/C级检修周期比率(N1,N2,…,NM),其中 M 为电力系统元件数目。
c.根据元件故障率函数和C级检修周期、A/C级检修周期比率,按式(5)求取各元件平均无效度,结合步骤a得到的m个削负荷状态及对应削负荷量,按式(7)、(8)求得系统可靠性指标 δLOLP、δEENS,按式(9)计算系统停电成本,按式(11)—(15)计算 A、C级计划检修成本、事后检修成本及系统总成本。
d.按式(24)计算系统总成本相对于各元件C级计划检修周期的灵敏度 βse=(βse1,βse2,…,βseM)。
e.若所有元件的灵敏度绝对值都不大于预设门槛值kesp,则转入步骤f。否则选出βse中最大和最小值所对应的元件序号分别计为h1、l1,做如下处理:若满足灵敏度 βseh1>kesp,令 Th1=0.99Th1;若 βsel1<-kesp,令Tl1=1.01Tl1,转入步骤 c。
f.按式(30)、(31)计算系统总成本相对于各元件A/C级检修周期比率N的前向差分ΔDe=(ΔDe1,和后向差分设其中“·”表示进行点乘运算。 若满足SDE中所有元素都小于0,则迭代算法结束。否则,做如下处理:找出SDE中大于0的元素对应的元件序号集合记为向量 p,寻找 ΔDe(p)中最小值和Δ最大值对应元件序号,分别计为令处理完毕后转步骤c。A/C级计划检修协调优化程序流程图如图4所示。
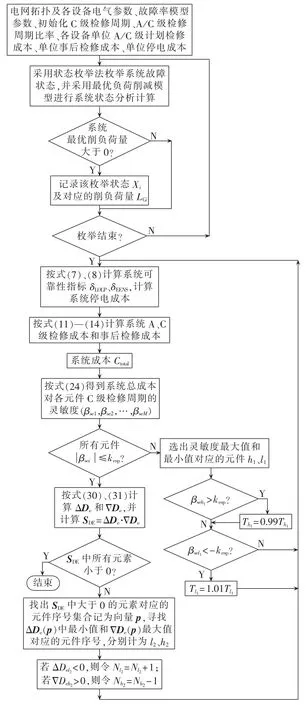
图4 A/C级计划检修协调优化程序流程图Fig.4 Flowchart of coordination and optimization of A/C-level preventive maintenance
5 算例分析
本文针对RBTS、IEEE-RTS79系统开展A/C级计划检修优化研究。
5.1 参数设置
设发电机C级检修材料费用与其类型和容量有关,如表1所示①中国华电集团公司安全生产部.中国华电生[2007]1653号.中国华电集团公司检修费、材料费限额标准,2007.。输电线路进行1次C级检修的材料费设为0.1万元/km。同时设α1、α2分别取原有故障率的60%和30%数值,β2取值为3。设施工费CW=0.012 万元 /h,单位停电成本 CL=0.05 万元/(MW·h),事后检修材料费取为C级检修材料费的1/3,A级检修材料费取为C级检修材料费的2.5倍。设C级检修的故障率恢复因子、役龄回退因子分别为a(i)=1+i/(8i+6),b(i)=i/(8i+6)。

表1 火/水电机组C级检修材料费参考标准Table 1 Material cost reference of C-level maintenance for thermal/hydro generation units
5.2 计划检修优化结果
5.2.1 RBTS系统计划检修优化
RBTS系统拓扑图如图5所示,其发电机位置如表2所示。
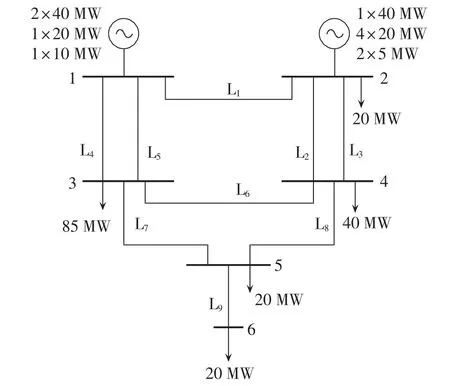
图5 RBTS系统拓扑图Fig.5 Topology of RBTS system
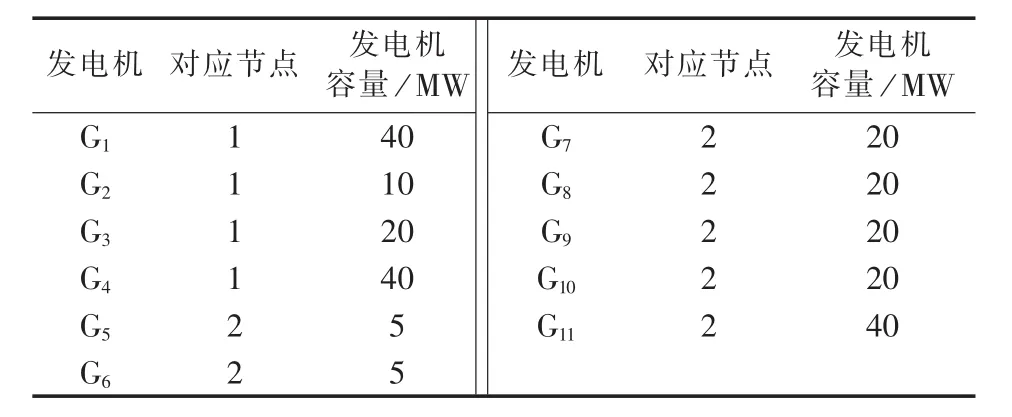
表2 RBTS发电机位置Table 2 Generating uint locations of RBTS
首先定义2种检修方式:方式Ⅰ为传统A/C级检修模式,即每年进行1次C级检修,5 a进行1次A级检修;方式Ⅱ为以检修成本和停电成本之和最小的A/C级优化检修方式。假设RBTS系统[21]发电机A和C级检修时间分别为事后检修时间的1.2倍和1.0倍,输电线路的A/C级检修时间为事后检修时间的1.5倍/1.2倍。计划检修优化结果如表3、图6—9所示。
从图6—9、表3可以得到以下几点结论。
a.从表3可以看出,方式Ⅱ相对方式Ⅰ总成本有所降低,而系统可靠性水平则大幅提升。其主要原因是方式Ⅱ下合理调整了A、C级计划检修成本,特别是A级检修成本的增加,显著提高了系统可靠性,事后检修成本和停电成本大幅降低,系统可靠性收益的增加大于计划检修成本的增大,使得系统总成本降低。
b.从图6、7可看出,除少数发电机、输电线路外,检修优化后各元件C级检修周期有所延长,A/C级检修周期比率则有所降低;从图8、9可看出,C级检修成本普遍降低,除线路L4—L8外,A级检修成本均有所增加。表明RBTS系统计划检修优化后更侧重于A级检修,以获得更大的检修效益。其中L4、L5本身可靠性较高,而L6—L8除本身可靠性较高外,其停运对系统充裕度影响也较小,因而L4—L8都降低了A级检修投入,以节约检修成本。
c.图8、9 中部分设备(如 G1、G3、G4)C 级检修周期缩短,而C级检修成本反而降低,原因在于C级检修成本由C级检修周期和A/C级检修周期比率N共同决定(如式(12)所示),虽然C级检修周期变短,但N降低导致平均每年分摊到的C级检修成本减少。
d.不同类型、容量和可靠性的电力设备对电网充裕度影响程度不同,优化后其最优C级检修周期和A/C级检修周期比率也不同,相应的A/C级计划检修投入也不一样。方式Ⅱ根据电力设备对电网充裕度贡献的大小对其A/C级检修周期进行了优化调整,加大了对电网充裕度贡献大的设备计划检修投入。如G1、G4为系统内大机组,其停运与否显著影响系统电源充裕度,因而优化后缩短了其A、C级检修周期,以换取更优的可靠性收益。
e.即使是完全相同的设备,其所在电网拓扑中位置不同,最优C级检修周期和A/C级检修周期比率也不一致,原因在于最优负荷削减模型中计入了网络拓扑信息,不同位置元件停运对电网充裕度影响不一致,优化将加大对系统内处于重要拓扑位置的设备计划检修投入。如线路L6—L9具有相同的电气和可靠性参数,但由于L9为负荷节点6单供线路,其停运直接导致节点6停电,因而优化后L9的C级检修周期和A/C级检修周期比率较L6—L8显著降低以提高其可靠性,降低失负荷风险。

表3 RBTS系统优化前后系统可靠性和系统各成本对比Table 3 Comparison of system reliability and costs between before and after optimization for RBTS system
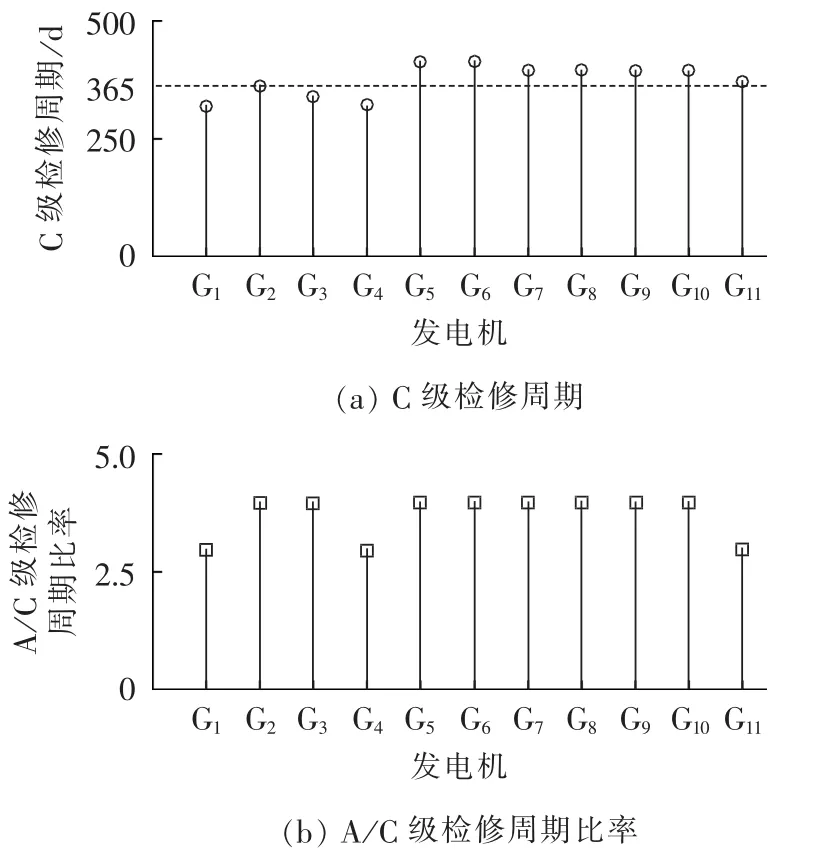
图6 发电机优化后C级的检修周期及A/C级检修周期比率Fig.6 C-level maintenance cycle and A/C-level maintenance cycle ratio after generator optimization
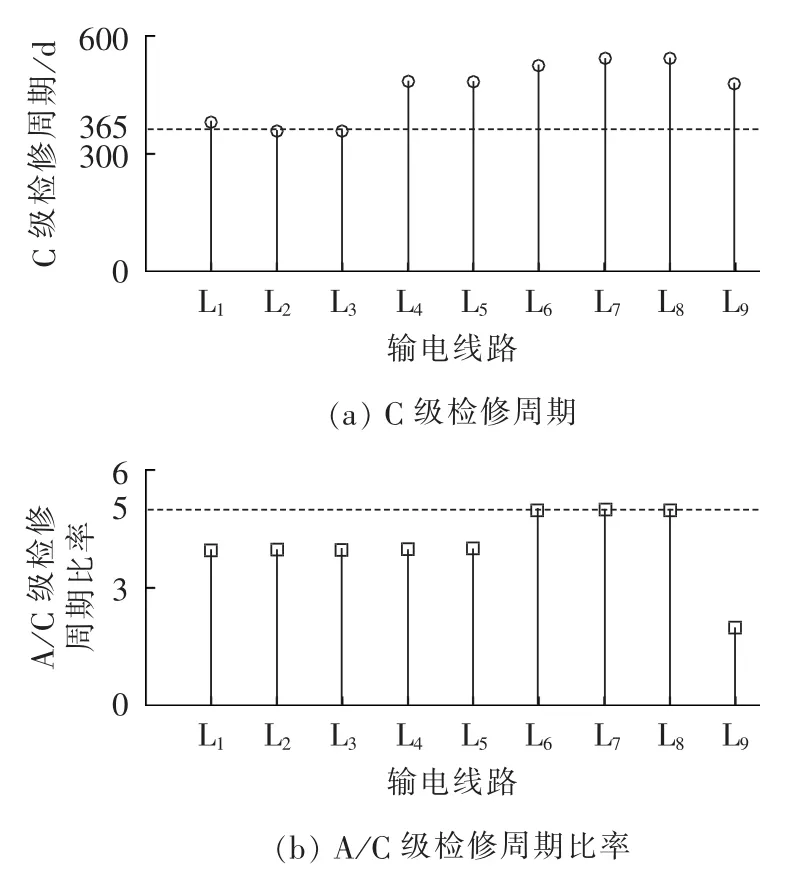
图7 输电线路优化后C级的检修周期及A/C级检修周期比率Fig.7 C-level maintenance cycle and A/C-level maintenance cycle ratio after transmission line optimization
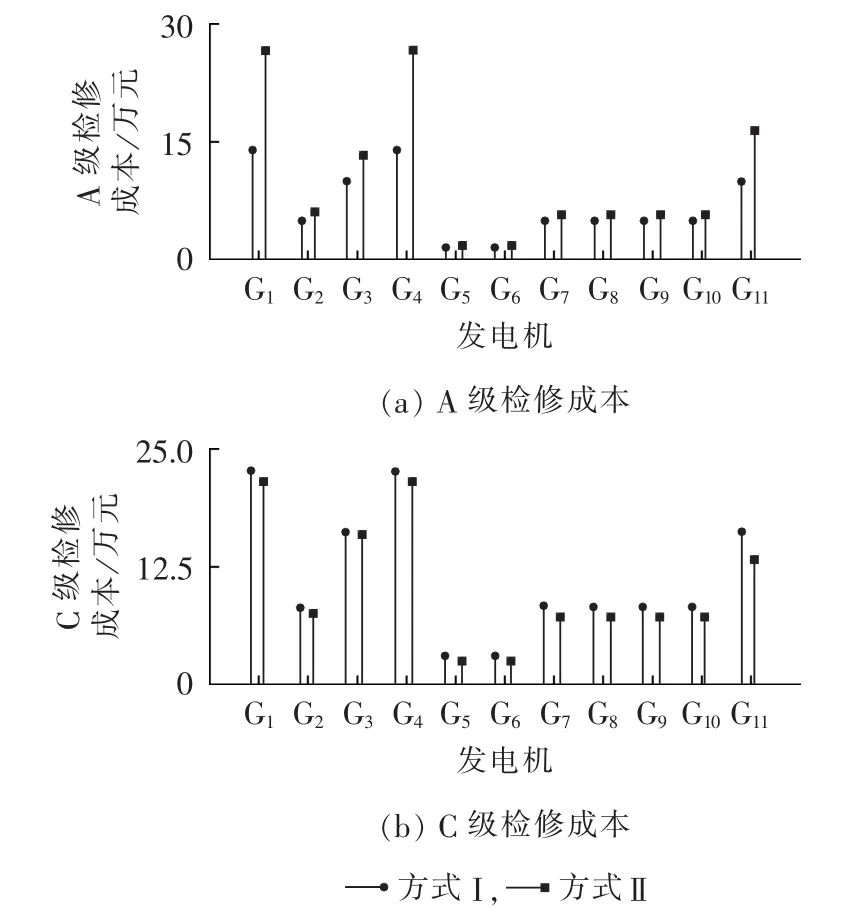
图8 发电机优化后A/C级的检修成本Fig.8 A/C-level maintenance cost after generator optimization
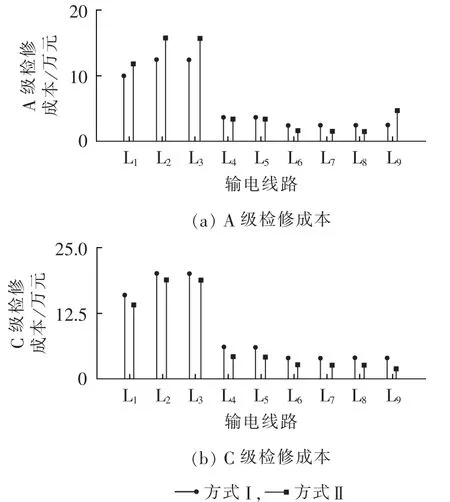
图9 输电线路优化后A/C级的检修成本Fig.9 A/C-level maintenance cost after transmission line optimization
5.2.2 IEEE-RTS79系统计划检修优化
IEEE-RTS79系统拓扑图如图10所示,其发电机位置如表4所示。
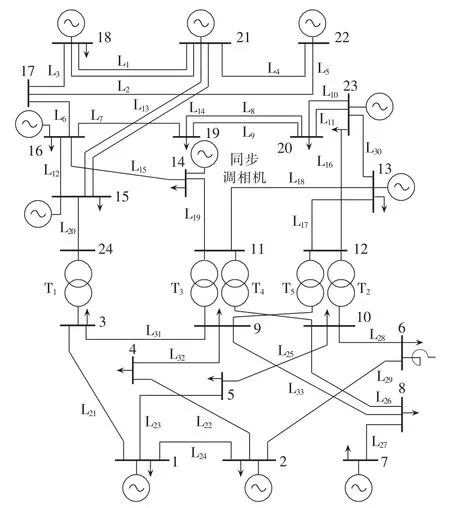
图10 IEEE-RTS79系统拓扑图Fig.10 Topology of IEEE-RTS79 system
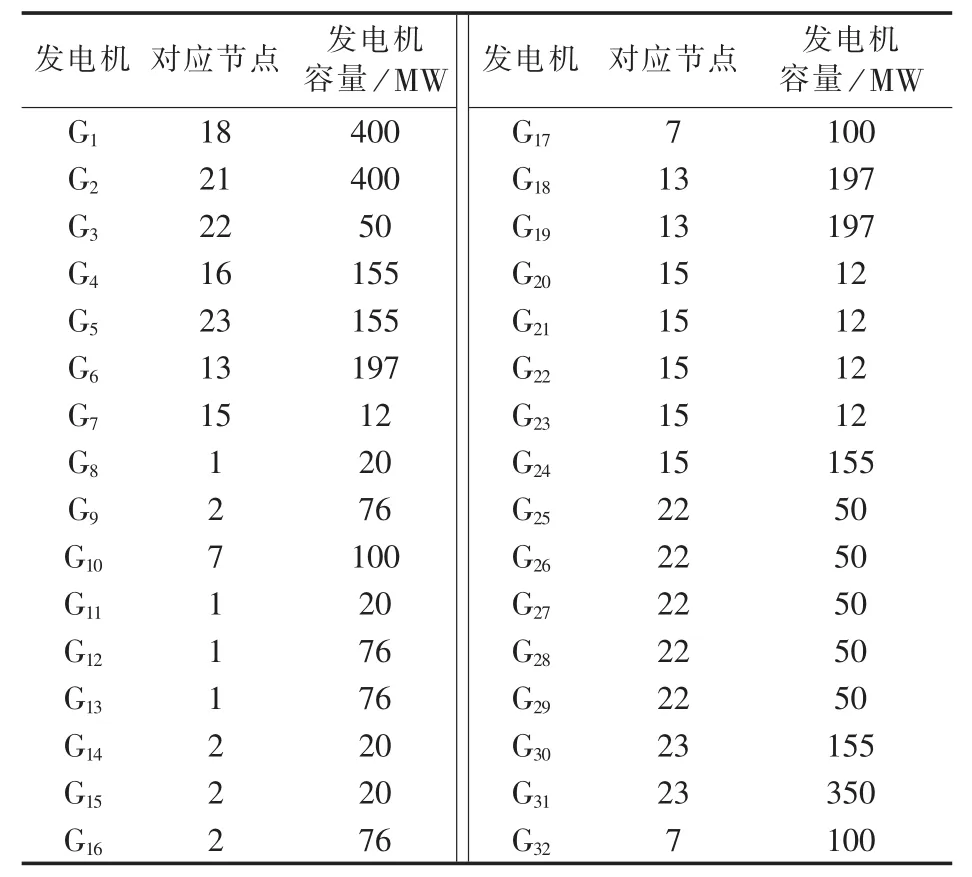
表4 IEEE-RTS79系统发电机位置Table 4 Generating uint locations of IEEE-RTS79 system
设 IEEE-RTS79 系统[22]发电机的 A/C 级检修时间为事后检修时间的1.6倍/1.4倍,输电线路的A/C级检修时间为事后检修时间的1.2倍/1.0倍,变压器A/C级检修时间为事后检修时间的80%/60%,其他假设和方式Ⅰ、Ⅱ定义与RBTS系统相同。
从表5和图11—13可以得到以下结论。
a.从表5可见,IEEE-RTS79系统计划检修优化后,系统总成本显著降低,降幅达13.34%;可靠性显著提高,其中 δEENS减少 59 019.82 MW·h,减少停电成本达2 950.99万元。其原因在于优化后合理调整了A/C级检修成本,特别是大幅增加了A级检修投入,使得系统可靠性显著提高,从而系统事后检修成本、系统停电成本显著降低。

表5 IEEE-RTS79系统优化前后系统可靠性和系统各成本对比Table 5 Comparison of system reliability and costs between before and after optimization for IEEE-RTS79 system
b.从图11—13可以看出,IEEE-RTS79系统经过计划检修优化后,发电系统大部分发电机C级检修周期有所缩短,A/C级检修周期比率普遍降低,尤其是对电源充裕度影响较大的系统内大容量机组G1、G2、G31表现最为显著,其 A/C 级检修交替进行;而输电系统中变压器和输电线路C级检修周期均有较大幅度的增大,除少数线路外A/C级检修比率保持不变或有所增加。原因在于IEEE-RTS79输电系统强大,少数输电元件故障对系统充裕度影响微小,且输电设备自身可靠性较高,因而优化后重点增加对系统充裕度影响较大的发电系统的计划检修投入以获得较高的可靠性收益。
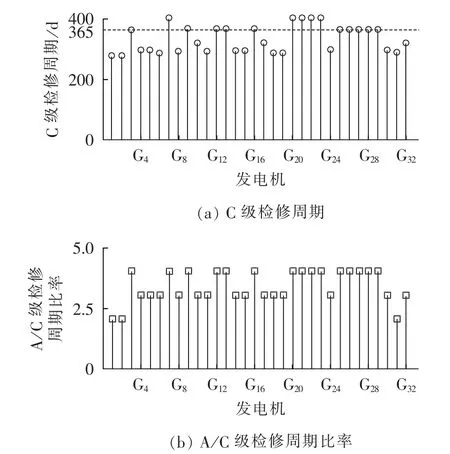
图11 发电机C级检修周期及A/C级检修周期比率Fig.11 C-level maintenance cycle and A/C-level maintenance cycle ratio of generators
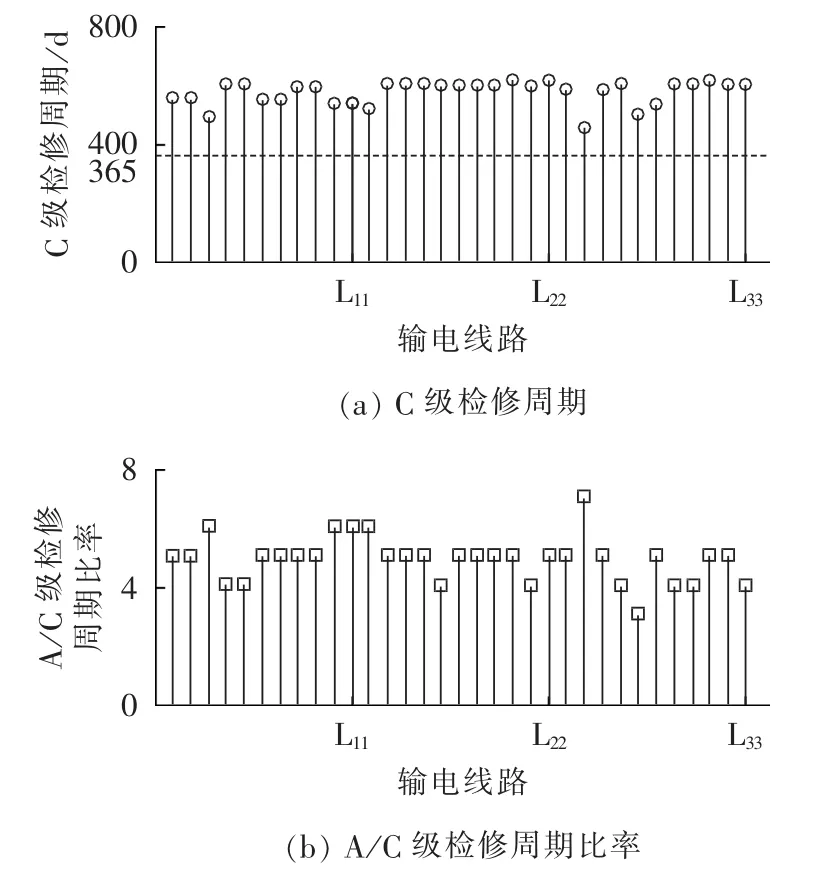
图12 输电线路C级检修周期及A/C级检修周期比率Fig.12 C-level maintenance cycle and A/C-level maintenance cycle ratio of transmission lines
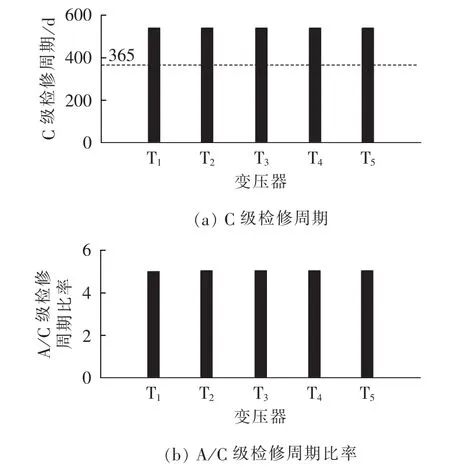
图13 变压器C级检修周期和A/C级检修周期比率Fig.13 C-level maintenance cycle and A/C-level maintenance cycle ratio of transformers
5.3 恢复因子变化对多级计划检修优化的影响规律
故障率恢复因子 a(i)和役龄回退因子 b(i)反映了电力设备进行第i次C级计划检修后的可靠性恢复效果,这里将(a(i),b(i))统称为恢复因子。 恢复因子越大,表明计划检修后元件可靠性恢复效果越差。本节通过逐步增大恢复因子,探索其对电网计划检修优化的影响规律。图14—16为恢复因子从初始值增大到初始值的1.8倍时,RBTS发电系统A/C级检修周期变化规律。
从图14—16看出,随着恢复因子的提高,优化后各发电机组C级检修周期大致呈增大趋势,而A级检修周期呈减小趋势,A/C级检修周期比率逐渐减小。原因在于,恢复因子越高,表明C级计划检修效率降低,故延长C级计划检修时间、减少C级检修次数以节约检修成本,而把资源投入到更有效的A级计划检修中,以获得最优的检修效益。此外,图16中G5、G6在恢复因子增大到1.2倍时A级检修周期相对于1.0倍时增大,原因在于G5、G6属于系统内最小容量机组,其停运与否对系统充裕度影响微小,在恢复因子处于1.0~1.2时,其对系统总成本影响的主导因素是机组本身的检修成本的变化,因而延长了其A/C级计划检修周期,以节约检修成本。
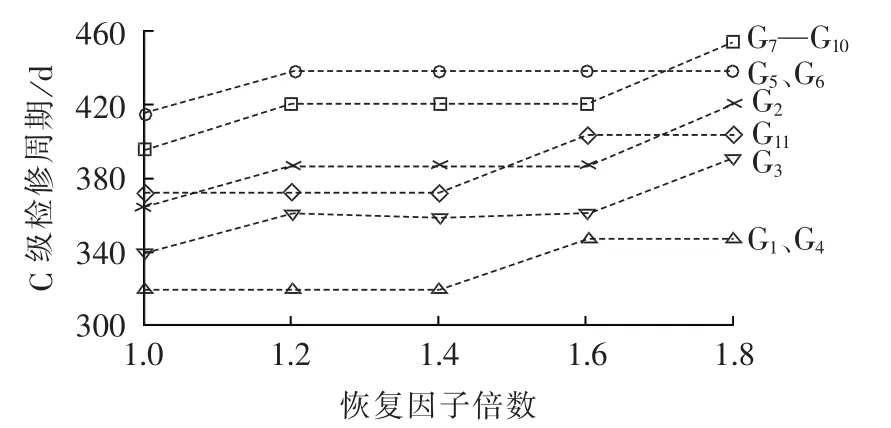
图14 各发电机C级检修周期随恢复因子倍数变化规律Fig.14 Relationship between C-level maintenance cycle and recovery factor for different generators
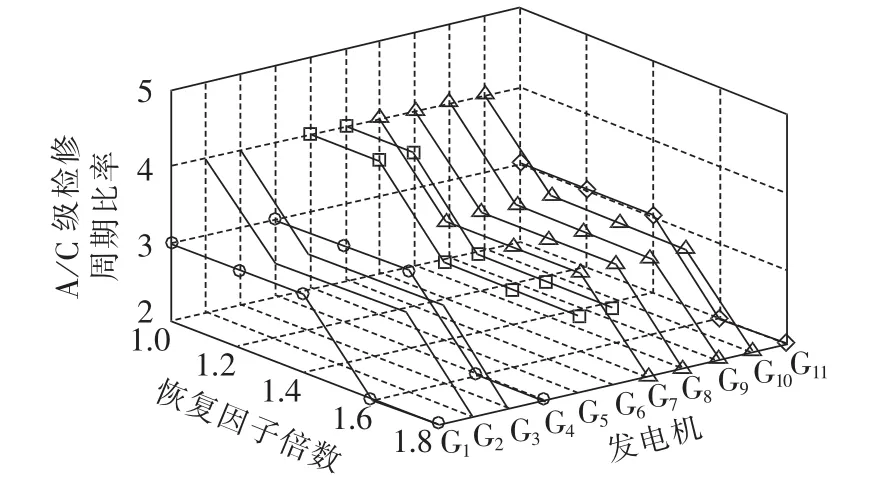
图15 各发电机A/C级检修周期比率随恢复因子倍数变化规律Fig.15 Relationship between A/C-level maintenance cycle ratio and recovery factor for different generators
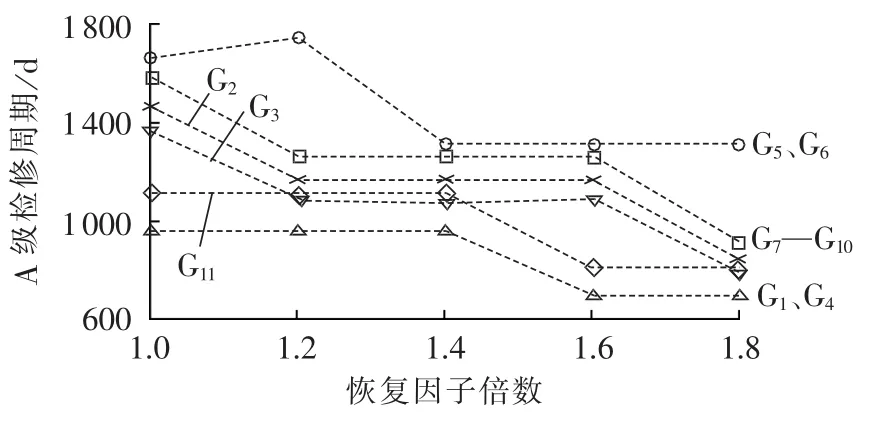
图16 各发电机A级检修周期随恢复因子倍数变化规律Fig.16 Relationship between A-level maintenance cycle and recovery factor for different generators
6 结论
本文计及电力设备故障率的时间增长效益,基于故障率函数和有效役龄建立了电力设备多级计划检修模型;建立了系统可靠性/经济性指标关于C级计划检修周期和A/C级检修周期比率的解析表达式;提出了融合灵敏度和差分思想的电网A/C级计划检修优化启发式迭代算法;通过RBTS、IEEE-RTS79系统验证了该算法的有效性,并对比分析了传统计划检修模式,探讨了C级检修恢复因子对计划检修优化的影响。分析得出以下结论。
a.基于灵敏度和差分思想的电网A/C级计划检修优化启发式迭代算法充分利用了灵敏度指标指示C级计划检修周期(连续型决策变量)最优调整方向,利用前向/后向差分指标指示A/C级检修周期比率N(整数型决策变量)最优调整方向,协调2类决策变量进行启发式迭代优化;此外,在整个优化过程只需进行1次最优削负荷计算,迭代过程直接通过解析表达式计算C级检修周期或A/C级检修周期比率调整后的系统可靠性指标,节省了大量计算时间。因此,该算法具有搜索效率高、计算速度快的特点。
b.不同类型、容量和可靠性的电力设备对电网充裕度影响程度不同,优化后其最优C级检修周期和A/C级检修周期比率也不同。即使是相同的设备,其所在电网拓扑中位置不同,由于最优负荷削减模型中计入了网络拓扑信息,最优C级检修周期和A/C级检修周期比率也不一致,优化将加大对系统内处于重要拓扑位置的设备计划检修投入。
c.探讨了C级检修恢复因子变化对A/C级计划检修优化结果的影响规律,结果表明C级检修恢复因子越高(C级检修效率越低),导致优化后更侧重于对元件可靠性恢复更有效的A级计划检修投入,以提高计划检修效益。

