多馈入直流系统的特高压直流接入方式优选方法

徐 箭 ，张华坤 ，孙 涛 ，王 甜 ，蒋一博 ，林常青

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.国网湖北省电力公司，湖北 武汉 430077）

0 引言

随着晋东南—南阳—荆门1000 kV特高压交流试验工程以及±800 kV向家坝—上海特高压直流工程的成功投运和安全稳定运行，我国进入了特高压交直流快速发展的新阶段。我国电网逐渐形成了交直流混联的格局，特别是华中、华东等受端电网将形成多回直流馈入特高压交流电网的运行方式，使得电网运行方式更加多样，电源安排更加灵活，对我国的能源资源优化配置具有重大作用。

多回直流馈入特高压交流电网使电网的结构更复杂，引起了一系列稳定性问题［1-2］：单个交流故障或直流故障有可能引发多回直流相继出现换相失败，严重时甚至会导致直流闭锁；直流一旦出现换相失败，在功率恢复过程中，需要交流系统提供大量的无功功率以确保足够的换相电压；多馈入直流系统还会使受端电网结构更加密集，加重受端的潮流和短路电流水平［3-7］。选择合适的直流落点和接入方式可减弱这些影响，使电网运行得更加安全、可靠、经济。

文献［8］兼顾交直流系统的稳定性和经济性，以线性加权法对单直流落点问题进行了研究；文献［9］以多馈入短路比为基础，通过建立整体性、均衡性、干扰性和安全裕度为指标的评价体系，采用二项加权系数法确立了多直流落点选择的方案；文献［10］定义了反映直流在交直流影响中的权重，基于多馈入短路比，对多馈入直流落点问题进行了研究。但是，这些研究都没有涉及特高压直流的接入方式问题。随着特高压交流网架的逐步建立，特高压直流接入交流电网的方式将有更多选择。目前对于特高压直流接入方式的研究还比较少，文献［11］从理论上分析了不同的特高压直流接入方式对多馈入短路比的影响，给出了特高压直流接入方式的参考，但是忽略了接入方式对其他指标的影响。

特高压直流接入方式的选择由受端电网的网架结构、安全稳定水平、经济性等多目标共同决定，各目标间的性质和量纲不同而无法统一比较，因此特高压直流接入方式优选属于典型的多目标决策MODM（Multiple Objective Decision Making）问题。MODM的求解有层次分析法、模糊优选［12-14］等。在求解的过程中，合理赋予权重是优选的关键。为了克服传统的只考虑主观权重而对主观经验依赖性较强或者只考虑客观权重而对数据依赖性较强的缺陷，近年来提出了考虑主客观权重的组合赋权方法［15-17］，但在组合系数的选取方面缺乏合理有效的方法。

本文不涉及特高压直流落点选择问题，仅对落点区域存在特高压交流变电站情况下直流的接入方式问题进行研究。文中首先建立了适用于多馈入直流系统的特高压直流接入方式的评价指标体系，该指标体系从网损、静态安全性、多馈入短路比等多个方面对特高压直流接入方式进行评价；然后分析了G1法和熵权法确定主客观权重的方法，并以主客观加权属性值一致化为目标求取了最优组合权重；在此基础上，以相对贴近度对特高压直流接入方案进行了优选；最后将该方法运用于“十三五”期间蒙西—武汉特高压直流接入方式的优选决策案例。

1 评价指标体系

1.1 评价指标选取原则

合理选择评价指标体系是正确决策的前提条件。因此在建立多馈入直流系统特高压直流接入方式评价指标体系时，指标选取应遵循一定的原则。

a.系统性。评价指标体系要能从各个角度系统地反映不同直流接入方式对系统运行特性的影响。

b.可量化性。应尽量选取能够量化或模糊量化的指标，便于优选。

c.典型性。应能够突出重点，把握问题的主要方面，同时评价指标间要有差异性和可比性。

在构建评价指标体系之前，首先要确定核心评价指标。核心评价指标的选取应该在遵循上述原则的前提下，突出问题的主要方面，并且易于计算分析。结合以上多馈入直流系统特高压直流接入方式的特点和目的，本文主要从经济性、安全性以及远景适应性3个方面选取了核心评价指标，构建了包含网损、静态安全、多馈入短路比、断面传输功率极限以及交流故障极限切除时间暂态稳定性指标的多馈入直流系统特高压直流接入方式的评价指标体系。

1.2 网损指标

网损反映特高压直流不同接入方案的运行成本，是经济性的重要指标。一般以式（1）进行计算。

其中，PG为所考察电网区域的总发电功率；PLD为所考察区域的总负荷功率。实际计算中，直接根据网络拓扑结构和运行方式，考察区域内的潮流水平，求取网络损耗。

1.3 静态安全性指标

静态安全性是指系统中线路、变压器等设备因故退出运行时电网设备的过载程度。静态安全性指标从潮流的角度反映了电网的安全供电能力。特高压直流不同接入方式下，网络内的潮流分布会发生变化，潮流过重会存在静态安全风险。当系统发生“N-1”故障时，可能导致部分线路功率超过其热稳极限。为了考核不同接入方案下的静态安全性，定义静态“N-1”安全性指标如式（2）和式（3）所示。

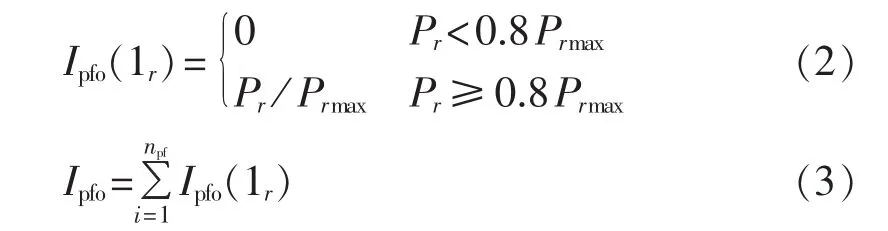
其中，Ipfo（1r）为静态“N-1”故障下第 r条线路静态安全值；Pr为第r条考核线路在静态“N-1”下的功率；Prmax为第r条考核线路的热稳极限；npf为考核线路总数；Ipfo为特高压直流不同馈入下的静态安全系数值。静态安全系数值越大，说明静态“N-1”下线路过载程度越大，静态安全裕度越小，静态安全性越差。

1.4 多馈入短路比指标

基于多端口戴维南等值的多馈入直流系统简化模型如图1所示。

图1 多馈入直流等值系统Fig.1 Equivalent multi-infeed DC system

多馈入短路比指标反映了受端交流电网对多馈入直流的电压支撑能力，可以用来衡量多馈入直流系统的电压稳定性［18］。交流系统对直流系统的电压支撑能力主要取决于受端交流系统与所连直流系统的容量的相对大小，即短路比指标［5，7，19］。 然而传统的短路比指标没有考虑多回直流之间的相互影响，所得结果往往偏于乐观。为了克服这个缺陷，2007年国际大电网会议（CIGRE）提出了多馈入短路比的概念［20］。其表达式如下：

其中，Mi为第i回直流所对应的多馈入短路比；Saci为第i回直流线路逆变侧母线的短路容量；Pdi、Pdj分别为第i、j回直流线路所传输的有功功率，MIIFji为直流线路相互影响因子，其定义为当换流母线i投入小容量的三相对称电抗器或电容器导致换流母线j电压变化ΔUj与换流母线i电压变化ΔUi的比值。

单回直流线路分层接入1000 kV及500 kV交流电网方式如图2所示［11］。对于分层接入方式，多馈入短路比同样适用，只是要分别求取单回直流线路所对应的2个换流母线的多馈入短路比。K回分层接入方式的直流线路就对应2K个多馈入短路比值。

图2 特高压直流分层接入方式Fig.2 Hierarchical UHVDC connection mode to AC

1.5 断面传输功率极限指标

断面传输功率极限指标反映了不同接入方式下特高压直流断面的可利用程度。断面输送功率极限越大，说明特高压直流断面的可利用程度越高，输送功率能力越强，断面抗干扰能力也越强，同时满足未来经济发展需要的传输裕度也越大。

本文定义断面传输功率极限指标值为：

其中，Plim为考虑系统静态和稳定性约束的特高压直流传输功率的极限值，可以用连续潮流算法计算得出；P0为特高压直流规划初始传输功率。

1.6 交流故障极限切除时间暂态稳定性指标

交流故障极限切除时间可以作为衡量多馈入直流系统暂态稳定性的重要指标。特高压直流接入区域附近重要母线出现三相短路故障时，会导致直流线路逆变侧换流母线电压下降，当其低于某一个值时，直流系统会出现换相失败，故障持续时间较长还会导致换流器因连续的换相失败而闭锁。直流线路闭锁会导致交直流系统损失较多有功，进而威胁系统安全稳定运行。交流故障极限切除时间值越大，多馈入直流系统抵御严重暂态故障的能力越强，暂态稳定性越好。

本文定义特高压直流不同接入方式下交流故障极限切除时间暂态稳定性指标tMDC为：

其中，NF为考察的特高压落点附近的故障母线总数；tMDC，i为母线i三相短路故障时能保持系统稳定的极限切除时间。

本文建立了多馈入直流系统特高压直流接入方式评价指标体系，具体为：网损指标Ⅰ，静态安全性指标Ⅱ，多馈入短路比指标Ⅲ，断面传输功率极限指标Ⅳ，交流故障极限切除时间暂态稳定性指标Ⅴ。其中，指标Ⅰ、Ⅱ为越小越优型指标，指标Ⅲ、Ⅳ、Ⅴ为越大越优型指标。

2 基于主客观最优组合赋权的优选方法

2.1 评价指标的规格化矩阵

设多目标系统是由n个方案组成的决策集，评价指标个数为m，可以形成方案决策矩阵如下：

其中，i=1，2，…，m；j=1，2，…，n；xij为决策方案 j指标i的值。

由于各评价指标之间存在量纲和级别上的差异，为了消除量纲和级别带来的不可公度性，决策之前首先将评价指标进行规格化处理［21］。

在优选决策过程中，取第i个评价指标的最大值与最小值分别作为上、下界限的相对值，引入相对优属度。 其中，最大值为 ximax=max（xi1，xi2，…，xin），最小值为 ximin=min（xi1，xi2，…，xin）。

对于越大越优型评价指标，其相对优属度为：

对于越小越优型评价指标，其相对优属度为：

由式（8）、（9）可得多目标决策的规格化矩阵R：

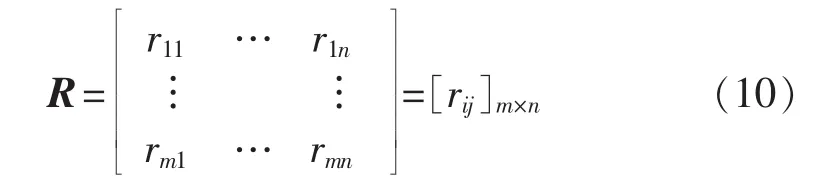
2.2 基于主客观加权属性值一致化的组合赋权

由于每个决策指标的重要性往往不同，需要为每个评价指标确定一个权值来代表其对决策方案的影响程度，权值的科学合理性会直接影响优选的结果，因此权值的确定非常关键。为了使权值既能反映决策者的主观愿望，又能体现决策的客观性，本文采用G1法确定主观权重，熵权法确定客观权重，并以主客观加权属性值一致化为目标求取主观权重和客观权重的加权系数，进而得到组合权重。

2.2.1 G1法主观赋权

设评价指标集为 D= ｛d1，d2，…，dm｝，G1 法通过逐次从D中选取最不重要指标，进而可唯一得到评价指标之间重要性的排序可以有效避免传统的层次分析法一致性检验错误的缺陷，同时对元素的个数没有限制，具有保序性［22］。

为书写方便且不失一般性，把重要性排序仍记为 d1>d2>…>dm。

专家关于评价指标dk-1与dk的重要性程度之比ωk-1/ωk的理性判断可以表示为：

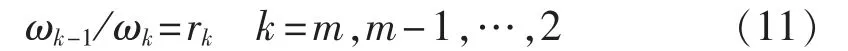
其中，ωk为评价指标dk的权重。

指标数量较大时，可以取最不重要的指标rm=1，为了使二元定量对比中rk更易于按我国的语言习惯给出定量标度，建立语气算子与定量标度之间的对应关系，如表1所示。一般情况下，最多需9个标度来区分事物之间质的差别或重要性程度的不同。

表1 语气算子与定量标度的对应关系Table 1 Corresponding relation between mood operator and quantitative scale

在给出rk的值之后，可确定指标的权重为：

ω=［ω1，ω2，…，ωm］即为指标的权向量。

2.2.2 熵权法客观赋权

在评价指标中所获得客观信息的多少，是评价精确和可靠的重要因素。熵是数据所含有效信息量的度量。通过熵来确定权重，就是根据各项评价指标值之间的差异程度，来确定各评价指标的权重［23］。

针对含m个评价指标的n个决策方案的决策问题，第i个评价指标的熵定义为：

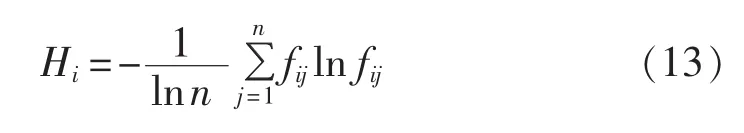
第i个评价指标的熵权ωi定义为：

从以上定义可以推出，决策方案的同一评价指标值相差越大，则熵值越小，熵权越大，表明该评价指标给决策者提供的有用信息越多；反之，决策方案的同一指标值相差越小，则熵值越大，熵权越小，该评价指标给决策者提供的有用信息越小。特别地，当评价指标值相等时，该项指标熵值为1，熵权为0，表明不提供任何决策有用信息，可以剔除。因此，熵权的大小并不是决策问题中评价指标真正意义上的重要性系数，它代表的是该评价指标在决策问题中所提供有效信息量的多寡程度，是主要依赖客观数据的客观评价方法。

2.2.3 基于主客观加权属性值一致化的组合赋权

在多目标决策方案中，各方案的优劣排序主要是由加权属性值决定。为了使主观信息和客观信息在方案排序中都能得到充分体现，本文建立了由主观权重确定的加权属性值与客观权重确定的加权属性值一致化的优化模型［24］。

方案j评价指标i的加权属性值分别为αω′irij、βω″irij，则方案j的主客观属性值偏离程度为：

为了使主客观加权属性值趋于一致，可建立优化模型如下：

由于各个方案之间是公平竞争关系，利用线性加权法可以把式（17）等价为如下模型：

通过对上述模型（18）进行求解，可求得评价指标主客观权重的加权系数。

2.3 基于相对贴近度的决策方案优选

在求取组合权重 ω=［ω1，ω2，…，ωm］之后，可求得加权属性矩阵G：

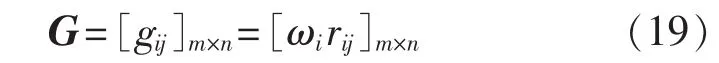
加权属性矩阵的理想点P*和负理想点P-分别为 P*=［p1，p2，…，pi，…，pm］、P-=［0，0，…，0，…，0］，其中

定义 Gj= ［g1j，g2j，…，gmj］，则各决策方案相对理想点的贴近度Tj为：

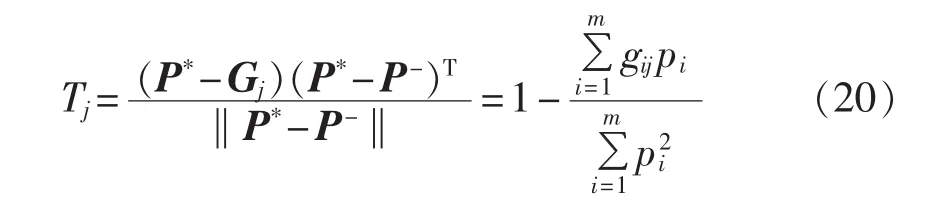
根据各方案算出的Tj值进行优选排序，Tj值越小则越优。

至此，本文建立了多馈入直流系统的特高压直流接入方式的评价指标体系以及最优组合赋权的优选方法，具体优选决策流程如图3所示。

图3 多馈入直流系统的特高压直流接入方式优选流程Fig.3 Flowchart of optimal connection mode selection of UHVDC to multi-infeed DC system

3 算例分析

华中电网作为我国主要的受端电网之一，需要接受大量外来电力。根据国家电网公司规划，“十三五”期间，华中电网将形成南阳—荆门—长沙、驻马店—武汉—南昌、万县—荆门—武汉的特高压交流网架，同时馈入直流线路5回，其中高压直流线路2回，特高压直流线路3回，构成了一个多馈入直流的系统。同时，为了满足蒙西风电外送以及鄂东经济发展的需要，蒙鄂±800kV特高压直流将落点武汉，输送功率8000 MW。根据规划，特高压直流接入受端电网的方案有3种，即接入500 kV交流网架，分层接入500kV和1000kV交流网架，以及接入1000kV交流网架，如图4所示。

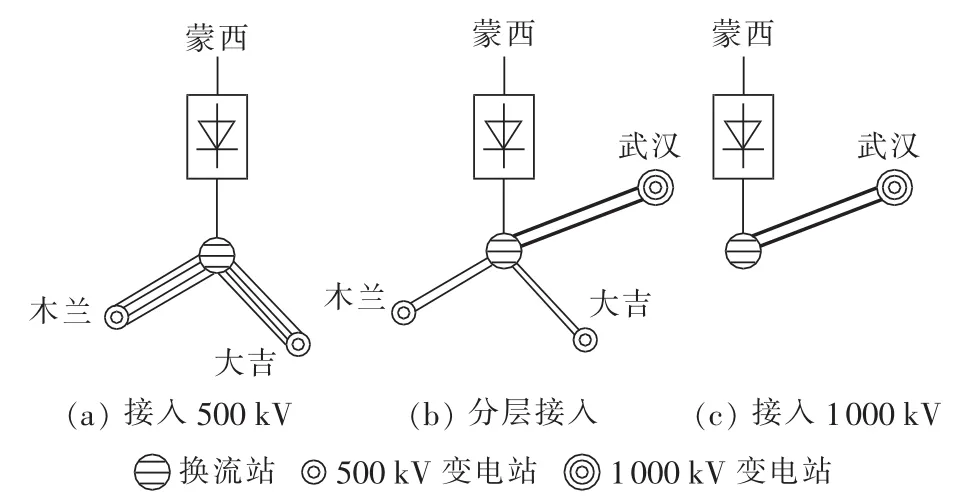
图4 蒙西—武汉特高压直流不同接入方式Fig.4 Different connection modes of West Mongolia-Wuhan UHVDC

将本文所提的多馈入直流系统特高压直流接入方式评价指标体系和优选方法应用到蒙西—武汉特高压直流接入方式选取中，可以确定m=5，n=3。

基于PSASP6.282建立蒙西—武汉特高压直流接入方式的3种仿真计算模型。各优选决策方案的网损指标Ⅰ、静态安全性指标Ⅱ、多馈入短路比指标Ⅲ、断面传输功率极限指标Ⅳ、交流故障极限切除时间暂态稳定性指标Ⅴ值如表2所示。其中分层接入方式多馈入短路比取500 kV换流母线和1000 kV换流母线多馈入短路比的平均值。

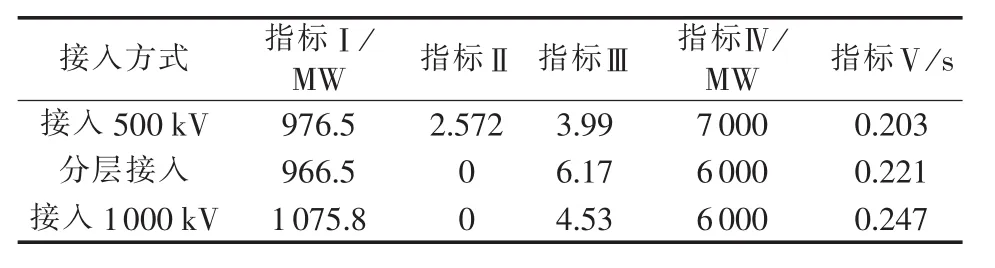
表2 不同接入方案的指标值计算结果Table 2 Calculated indexes for different connection modes

将指标值规格化处理后可得接入方式目标优属度矩阵为：

3.1 组合权重的计算

根据多馈入直流系统特高压直流接入对电网的影响，可以确定评价指标的重要性排序为多馈入短路比指标Ⅲ>静态安全性指标Ⅱ>交流故障极限切除时间暂态稳定性指标Ⅴ>网损指标Ⅰ>断面传输功率极限指标Ⅳ。结合G1法比较指标间的重要性，可得评价指标的主观权重向量为ω′=［0.137 6 0.231 2 0.3237 0.1147 0.1927］，由式（13）、（14）可得基于熵权法的评价指标的客观权重向量为 ω″=［0.002 6 0.9428 0.0406 0.0064 0.0077］。

解模型式（18）可得主客观权重组合系数分别为α=0.7015、β=0.2985，于是可求得组合权重向量为ω=［0.0973 0.4436 0.2392 0.0824 0.1375］。

3.2 决策方案的相对贴近度

基于组合权重向量和优属度矩阵可求得加权属性矩阵为：

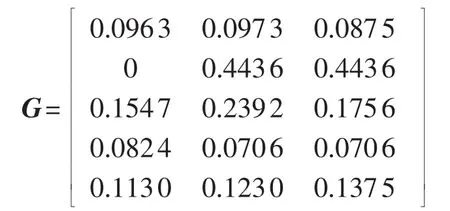
对3个决策方案分别求其对理想点的相对贴近度，可得 T1=0.7624，T2=0.0103，T3=0.0593。 因此方案2即特高压直流分层接入方式最优。

表3 给出了分别基于线性加权和法［8］、灰色综合方法［14］、模糊优选方法［16］的特高压直流接入方式优选结果。

表3 基于不同优选方法的特高压直流接入方式优选结果Table 3 Results of optimal connection mode selection for different selection methods

本文的优选结果与表3中采用各种方法所得优选结果一致，验证了本文方法的有效性。同时，对特高压直流分层接入方式下的电网进行各种安全稳定性校核仿真，结果表明此种方式下电网潮流分布均匀合理，线路变压器等均未过载，静态安全分析能够通过，单一故障暂态稳定校核（即“N-1”暂态稳定校核）和严重故障暂态稳定校核（即“N-2”暂态稳定校核）均能达到安全稳定标准，验证了分层接入方式的合理性以及本文所提方法的可行性。因此，“十三五”期间，蒙西—武汉特高压直流接入方式可优先考虑分层接入500 kV和1000 kV交流网架。

4 结论

随着我国特高压交直流的快速发展，多馈入直流的电网越来越多，特高压直流的接入方式也不再局限于受端500 kV交流网架，研究特高压直流的接入方式具有重要的实际应用价值。本文建立了一套考虑电网的网损、静态安全稳定性、多馈入短路比等重要因素的评价指标体系，全面考虑了特高压直流接入对电网的影响。分析了以主客观加权属性值一致化为目标的最优组合权重求取方法，并以相对贴近度指标来量化评估各接入方案。最后，将所提的优选方法应用于“十三五”期间蒙西—武汉特高压直流接入方式的优选中，得出最优接入方案为分层接入500 kV和1000 kV交流网架。

本文所提评价指标概念明确，全面考虑了特高压直流接入的影响，优选方法简单，易于实现。所提方法也可以为多馈入直流系统多回特高压直流接入方案的优选决策提供一定的参考。