区域交通网络的最优配置问题研究

张其强，常玉林，2，邱大为，张 鹏

(1.江苏大学 汽车与交通工程学院，江苏 镇江 212013;2.东南大学城市智能交通重点实验室，南京 211189;3.重庆育才成功学校，重庆 400051)

区域交通网络的最优配置问题是近年来交通领域的研究热点之一，研究区域交通网络的最优配置问题为区域交通网络配置的科学、合理规划提供理论支撑，同时进一步丰富了最优化理论与方法的内涵。

近年来，许多研究人员对区域交通网络的优化配置问题进行了大量的研究，取得了一定的研究成果。文献［1］以公交公司总效益最大、乘客的总出行时间最短和对环境的影响为优化目标建立公交线网模型，并给出了与优化目标相对应的约束条件;文献［2］建立了交通方式划分与交通分配组合模型，优化了经济圈范围内的客运多方式的交通网络结构，并通过建立与该均衡条件等价的变分不等式模型来研究乘客的交通方式选择问题;文献［3］构建了区域公路交通预测模型，提出了“线－面－体”预测方法，建立了干线公路网等级结构优化模型，给出了公路网交通评价的指标及方法。

现有文献中的研究成果对区域交通网络最优配置的研究还存在一些不足:大量研究集中在公交公司发车数量最少的问题上，而忽略了公交车的拥挤程度;在考虑缩短乘客的候车时间的具体问题上，没有涉及候车乘客流失对公交公司效益所造成的损失;在追求公交公司总效益时，没有考虑到社会总效益。本文运用机理分析方法建立多目标的交通优化模型，并用非线性规划理论优化多目标整式模型。本文的研究是对公交车的载客量有一定限制，从而降低拥挤程度;对乘客的候车时间及上下车时间作出了限制，考虑了超出限制范围的候车乘客流失对公交公司效益所造成的损失，并在此基础上得到公交车票价的求解方式。由乘客的候车时间和上下车时间求得乘客的总逗留时间;由各条公交线路各个站点在单位时间内的上下车人数为基本数据，得出公交车拥挤程度;从而建立以公交公司效益最大、乘客的逗留时间最短以及公交车拥挤程度最低的多目标优化模型。

最后，以重庆两江新区为例，利用Matlab软件对模型进行数值实验，从而获得优化模型以及区域交通网络配置的最优方案，继而解决区域交通网络配置的实际问题，并满足社会需求。

1 交通网络配置相关因素分析

综合调查分析表明:近些年来，随着城市经济快速发展，城市化进程加快，交通需求日益增长，交通问题日显突出，特别是道路客运交通问题。下面对区域交通网络配置中的一些相关因素进行分析。

1)路网布局不合理。道路客运线路受城市发展不均衡和道路网结构不合理的影响。这种不合理制约了经济的发展，降低了道路的服务水平。

2)公交线网功能单一，缺乏明确的的层次结构。公交线路缺乏功能或等级上的划分，各线路功能一致，不能充分地利用各自的资源条件。

3)站点数量不足，站点布局不合理，导致车辆配置不能满足居民出行需求。不利于协调客运车辆运营和开发城市用地。受用地条件限制，公交线路缺乏港湾停靠站，导致客运车辆占道停靠现象严重，造成道路通行能力下降。

4)客运车辆运力投入不足，运力分配不合理。在交通高峰时段，客运车辆运力的不足和分配的不合理性，导致部分线路抢客、赖站现象严重，而部分地区居民乘车又困难。

5)公交公司对公交车超载没有限制，使得服务质量下降。公交公司对公交车超载率无限制，导致上车人数无节制，从而使乘客的满意度降低。

随着城市的发展，其交通网络配置应满足社会需求。一个地区的经济发展带动区域经济的发展、人流量的增加，导致乘坐公交车的人数增加。针对这种情况，公交公司应该协调好现在的客流需求与车辆配置，以适应并满足未来人口增长、交通工具多样化等区域交通网络配置的最新需求。

2 区域交通网络配置指标分析

2.1 基本假设

1)公交公司内同一路线各辆车的规格相同;

2)同一线路的公交车行驶每公里的成本为固定值;

3)公交车各条线路独立运行，相互之间无影响;

4)公交车匀速行驶，不考虑塞车和行车事故等情况;

5)公交公司有足够多的车辆，可以服从任一公交线路调度;

6)乘客出行选择固定公交线路;

7)每个乘客来到车站是相互独立的，乘客到达车站后开始排队，在各个车站候车乘客的数量服从泊松分布;

8)当车到达时，排队等车的乘客以先到先上的原则按顺序上车，下车的乘客也是按顺序下车。乘客上下车服从指数分布。

2.2 符号说明

本文涉及的主要变量和参数如下:

k:公交车路线条数;

a:单位时段的时间长度(min);

ni:第i条线路每天运行的时段数;

pi:第i条线路各站点上车乘客票价的期望(元)，i=1，2，…，k;

c:未能上车的乘客与当时段候车人数的比值;

ai:第i条线路第1段的最大站点数，i=1，2，…，k;

bi:第i条线路第2段的最大站点数，i=1，2，…，k;

ci:第i条线路第3段的最大站点数，i=1，2，…，k;

ti:第i条线路每天通车的总时间(min);i=1，2，…，k;

μib:在b时段第i条线路乘客平均上下车时间(min/人);i=1，2，…，k，b=1，…，ni;

tijbmax:在b时段第i条线路第j站点乘客的最长等待时间(min)，是公交公司承诺的服务标准，i=1，2，…，k，j=1，2，…，Ai，b=1，…，ni;

mi:第 i条线路的总站点数(个)，i=1，2，…，k;

Di:第i条线路起点到终点的总路程(km)，i=1，2，…，k;

Mi:第i条线路的每辆公交车的标准载客量(人)，i=1，2，…，k;

Mimax:第i条线路的每辆公交车的最大载客量(人)，i=1，2，…，k;

Mimin:第i条线路的每辆公交车的最小载客量(人)，i=1，2，…，k;

U:公交公司所获收入(元);

Ui:第 i条公交车所获收入(元)，i=1，2，…，k;

Vi:第i条公交车每运行每公里的单位成本(元)，i=1，2，…，k;

VF:公交公司每天的固定成本(元);

VFi:第i条公交线路每天的固定成本(元)，i=1，2，…，k;

V0:公交公司的总营运成本(元);

W:因乘客流失而造成的损失(元);

R1:社会总效益;

R0:公交公司的总效益;

N:城市公交车辆标台数;

P:城市人口数;

Nib:第i条线路在b时段的发车数量(辆)，i=1，2，…，k，b=1，…，n;

T:乘客的总逗留时间(min);

Tib:第 i条线路在 b时段起点站发车周期(min/辆)，i=1，2，…，k，b=1，…，ni;

Ti:第i条线路高峰期起点站发车周期(min/辆)，i=1，2，…，k，b=1，…，ni;

αimax:第i条线路公交车的最大满载率;

Qijb(x):第i条路线第b时段第j个站点到第j+1个站点期间拥挤程度，x为公交车上的人数，i=1，2，…，k，j=1，2，…，Ai，b=1，…，ni;

Q:公交车总拥挤程度;

li:公交线网中第i条公交线路的长度(km)。

2.3 区域交通网络公共交通定价标准

一般认为乘客上车之后，在之后的每个站点下车的概率是相等的，满足均匀分布。将第i条交通线路的票价分为以下4种情况:① 乘客上车之后在前ai个站点下车的票价;②乘客上车之后在第ai+1个站点到第bi个站点下车的票价;③乘客上车之后在第bi+1个站点到第ci个站点下车的票价;④乘客上车之后超过ci个站点下车的票价(i=1，2，…，k)。

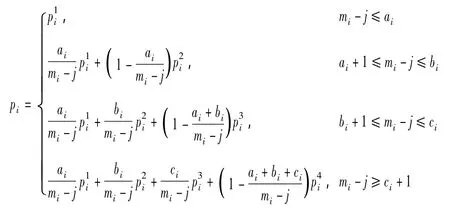
2.4 区域交通网络公共交通总效益

区域交通网络系统的总效益函数为:

其中，U是公交公司的营运收入，为所有上车人数乘以公交公司规定票价，

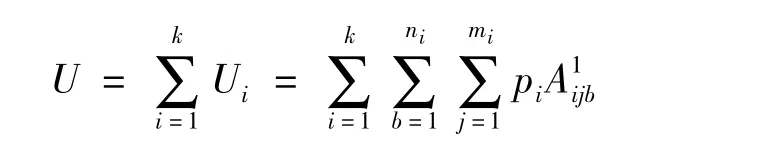
V0是公交公司的营运成本，为运行总距离(km)乘以每公里单位成本加上每天固定成本，

W是候车人离去而造成的损失，为总候车人数与总上车人数之差乘以乘客应付票价

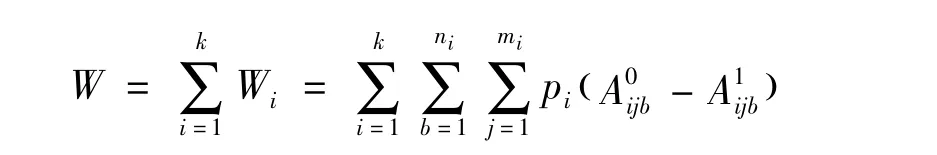
将以上所得代入式(1)得区域交通网络系统的总效益函数如下:

2.5 不同时段区域交通网络公共交通系统逗留时间

乘客在站点的逗留时间包括候车时间和上下车时间。计算乘客的逗留时间，用以下定理。

根据以上定理，乘客于第i条路线第b时段第s辆车进站的到达时间是一个分布在(sTib，(s+1)Tib)上的均匀随机变量，s=1，2，…，Nib，即乘客候车时间(排队时间)的期望为:

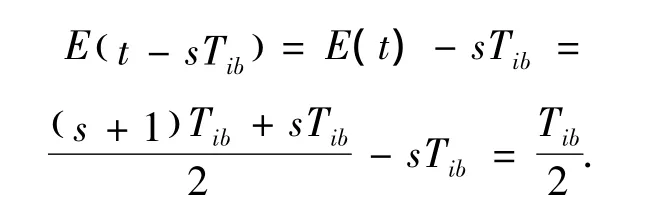
在第i条路线第b时段，当车当达时，乘客开始上车和下车，这个过程服从参数为μib的指数分布，则每个乘客上下车的期望为1/μib。因此，一个乘客在上下车时浪费的时间为

又因为第i条路线第b时段的发车次数Nib与起点站的发车周期Tib之间的关系为

因此，每位乘客的逗留时间等于候车时间和上下车的时间，为

2.6 区域交通网络公共交通拥挤程度

通过拥挤程度来刻画当公交车出现超载时就会拥挤。下面定义第i条路线第b时段第j个站点到第j+1个站点期间拥挤程度与车上乘客数之间的关系满足如下:

1)当公交车上乘客数不超过该公交车的标准载客数Mi:Qijb(x)=0;

2)当公交车上乘客数为该公交车的最大载客数Mimax:Qijb(x)=1。

当公交车上乘客数从超过该公交车的标准载客数到乘客数为该公交车的最大载客数时，公交车上乘客数与拥挤程度呈线性关系，则通过1)与2)可得:

通过上述函数可得出第i条路线第b时段第j个站点到第j+1个站点期间公交车上的人数为

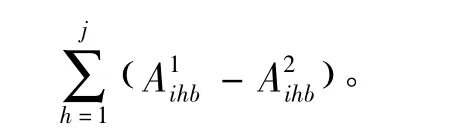
则一天之中所有公交车的总拥挤程度为:

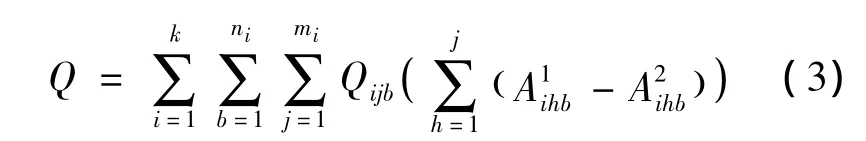
2.7 区域交通网络主要约束

一方面，乘客逗留时间的约束为:第i条路线第j个站点第b时段乘客的逗留时间应小于tijbmax(即公交公司承诺的服务标准)，则乘客逗留时间应满足

联合式(2)，则第i条路线第b时段的发车次数应满足

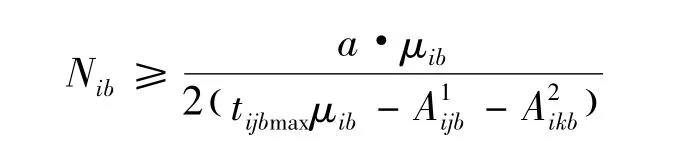
另一方面，公共交通载客量约束为:第i条线路第b时段公车第h站到第h+1站期间在车上的人数与该时段发车次数应该满足

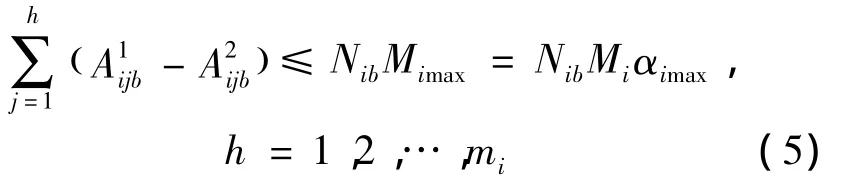
再者，每辆公交车的平均载客量不应低于最小载客量。在第i条线路中，利用公交车从第h站到第h+1站期间在发车的累加人数除以发车次数来刻画平均载客量，则有

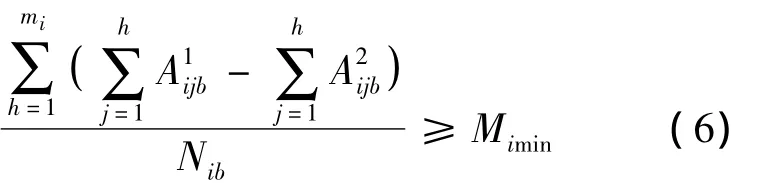
3 区域交通网路系统最优配置多目标优化模型

区域交通网络是区域发展的重要影响因素之一。因此，区域交通网络的配置对区域发展起至关重要的作用。凯恩斯在《通论》中指出，一个部门的新增投资，不仅会使该部门的收入增加，而且会通过连锁反应引起其他有关部门的收入增加，同时可通过连锁反应，引起其他有关部门追加新投资获得新收入，致使国民收入总量的增长若干倍于最初那笔投资，这就是所谓的乘数效应［5］。结合乘数效应原理考虑区域公共交通配置给区域发展带来的综合效益，建立区域公共交通网络配置对区域乘客的服务能力、公交公司效益、区域经济发展协调程度的最优化模型，从而使三方的利益达到充分均衡［6］。

建立多目标优化模型:

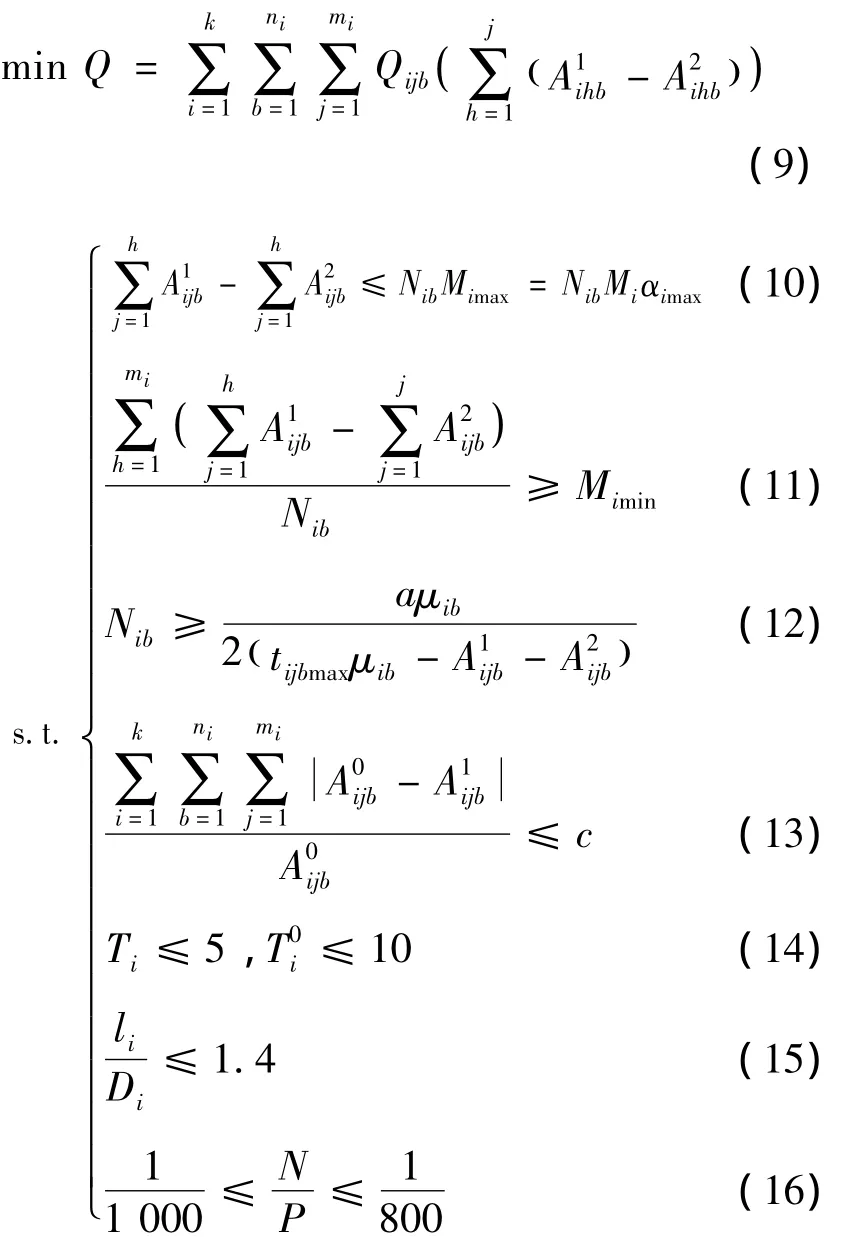
约束条件(10)、(11):b时段第i条路线在第j个站点的运载乘客数量范围;

约束条件(12):通过第i条路线第j个站点第b时段乘客的逗留时间应小于tijbmax(即公交公司承诺的服务标准)，计算得出的第i条路线第b时段的发车数量(辆);

约束条件(13):b时段第i条路线在第j个站点处未能上车的乘客数量与b时段第i条路线在第j个站点的候车总人数比值应不大于某一个较小的常数。

约束条件(14):在平常时段乘客侯车时间一般不超过10 min，在高峰时段一般不超过5 min。

约束条件(15):公共交通线路长度与起、终点空间直线距离之比，称为公交线路的非直线系数。结合实际特点，线路非直线系数可采用线路的行程长度与起、终点间可通行公交的城市道路的最短长度之比来衡量。

约束条件(16):根据《规范》中的要求，大城市的公交车辆保有量的满足范围。

4 模型数值实验结果

1)针对重庆两江新区目前的综合效益，其交通网络最优配置

通过调查收集各公交线路的上下车人数、各线路的各站点处每位乘客的逗留时间、个人票价、公交公司固定成本以及公交公司的潜在收入等数据，综合分析区域公共交通网络给区域创造总效益，利用Matlab软件进行数值实验，算出最大协调程度下的最优值。

表1 发车周期对总效益、逗留时间、拥挤程度的影响

通过考虑因素、计算结果评价区域公共交通的服务能力，提炼出最优模型。

2)2015年针对区域综合效益，两江新区交通网络的最优配置

了解目前两江新区的交通方案网路，分析其动态发展，并结合其未来发展规划给出2015年针对区域综合效益，两江新区交通网路的最优配置方案:

表2 2015年两江新区交通网络的最优配置

5 结束语

本文研究有关区域交通最优配置的问题，追求的效果是尽量缩短乘客的候车时间，降低公交车的拥挤程度，减少公交公司派出的车辆数。要使乘客的候车时间缩短、公交车拥挤程度降低，则公交公司需缩短发车间隔，从而必然导致派出的车辆数增加、公共公司的经济效益下降。这说明候车时间、拥挤程度与发车数量存在矛盾，即一个量的减少(增加)必然会导致另一个量的增加(减少)。本文正是在一定条件下给出区域交通网络最优配置与最优规划的方案，从而使客流需求与车型配置协调程度最大化。研究区域交通网络的最优配置问题具有十分重要的理论意义和应用价值。

［1］王胜辉.城市公交线网的优化设计［J］.科技信息，2006(6):69－71.

［2］李爽，邓卫，吕宜生.经济圈客运交通方式分担与交通分配组合模型［J］.东南大学学学报:自然科学版，2009，39(4):854 －858.

［3］裴玉龙，张树升.区域干线公路网规划理论的研究［J］.哈尔滨建筑大学学报，1995(2):106 －114.

［4］姜启源.数学模型［M］.2版.北京:高等教育出版社，1993.

［5］约翰·梅纳德·凯恩斯.就业、利息和货币通论［M］.魏埙，译.西安:陕西人民出版社，2011.

［6］GB50220—95.城市道路交通规划设计规范［S］.北京:中华人民共和国建设部，1995.