基于BP神经网络的电控发动机故障诊断研究

李志鹏，邵宪友，张东兴，杨传英

(东北林业大学交通学院，哈尔滨 150040)

为突破传统的以技艺与经验为主的汽车发动机故障诊断技术的瓶颈，建立以现代技术为基础的故障诊断新理论，逐渐完善诊断系统的科学理论体系成为当今发动机故障诊断领域的重要发展趋势。

人工神经网络(artificial neural network，ANN)是对生物或人脑神经网络的抽象表现，建立的模型以类似自然界生物的交互方式适应环境，具备从周围环境学习的能力。以认知神经科学和脑科学理论为基础的神经网络为实现自动化控制、处理复杂问题提供了更多有效的途径。其中BP神经网络能够以任意计算精度逼近控制系统的非线性函数，因而得到了非常广泛的应用［1－9］。同时，BP网络还能以较高的运算效率对所接受信息并行处理，自我学习能力、组织性以及创造性较强，且具有很好的鲁棒性和容错性，在汽车故障诊断领域具有广阔的发展前景。

1 BP神经网络结构及原理

BP(Back-Propagation)神经网络算法不仅包括输入与输出节点层，而且还有隐含节点层，其中隐含层可以是单层，也可以是多层。只要具备充分多的隐含层单元数，就能够以任意计算精度逼近任意有限维函数。图1为3层 BP神经网络模型［10］。

图1 3层BP神经网络模型

设输入层神经元有 n个，xi(i=1，2，…，n)表示其输人，隐含层内有l个神经元，bh(h=1，2，…，l)表示隐层的输出，输出层内有m个神经元，yj(j=1，2，…，m)，网络的输入矢量 X=(x1，x2，…，xn)，中间层输出矢量为 B=(b1，b2，…，bl)，则有

式中:vhi为输入层到隐含层的权值;θi为隐层的阈值。输出层的输出矢量Y=(y1，y2，…，ym)，则有

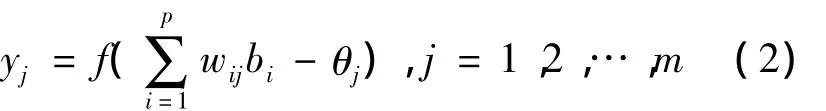
式中:wij为隐含层到输出层的权值;θj为输出层的阈值。

式(1)、(2)中 f(·)为激活函数。一般情况下，f(·)不能为线性函数，否则神经网络不能实现非线性映射特性。选取Sigmoid函数(简称S函数)，其表达式为，系数λ取决于函数的压缩程度。

BP算法的基本原理:网络的学习过程由信号的正向传播与误差的反向传播组成。正向传播时，输入样本从输入层输入，经各个隐含层处理后传向输出层。如果输出层的实际输出与期望的输出不符，则算法转入误差反向传播阶段。误差反向传播阶段是将输出误差以某种形式经过隐含层向输入层逐层反传，并将误差分摊给各层的所有神经元，从而获得各层神经元的误差信号。此误差信号被作为修正各个神经元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程周而复始地进行，权值也在不断地调整，这就是网络的学习训练过程［11］。BP网络学习的实质就是求取误差函数最小值的问题。该算法采用学习规则，按误差函数的负梯度方向修改权值。

2 BP网络训练仿真程序

在无负荷怠速(800 r/min左右)和加速工况(1800 r/min左右)的两种状态下，以韩国现代公司生产的Grander系列V63000汽油发动机为实验对象，人为设置发动机常见的6种故障类型，即无故障(正常状态)、空气流量传感器故障、节气门位置传感器故障、氧传感器故障、点火线圈故障、喷油器故障。利用X－431诊断仪和AUTO5－1型尾气分析仪测量传感器故障数据流与尾气排放故障的信息。

训练样本集(即故障征兆集)应适用于对网络进行学习训练，其对故障诊断起着关键的作用。训练样本集不仅应全面涵盖所选故障模式类的数据，还应具有一定的代表性，并且还必须保证学习的有效性。表1是各类故障对应的理想输出值。

当相应的故障发生时，其故障模式位输出代码为1。

本文采用传统的3层BP神经网络对电控发动机故障进行诊断，输入数据为提取的相应数据流信号特征值，输出是对故障原因进行的相应编码。以发动机转速、节气门开度传感器、空气流量传感器、氧传感器、空气温度传感器及发动机的排放信息的特征值作为网络的输入值，以理想的输出作为网络输出值。执行器、传感器故障特征因素及故障原因如表2所示。

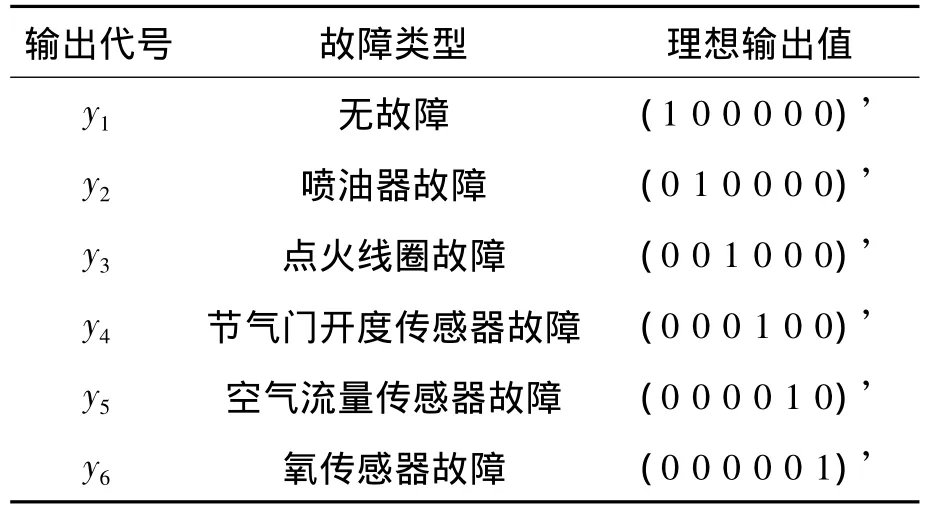
表1 各种故障对应的理想输出值

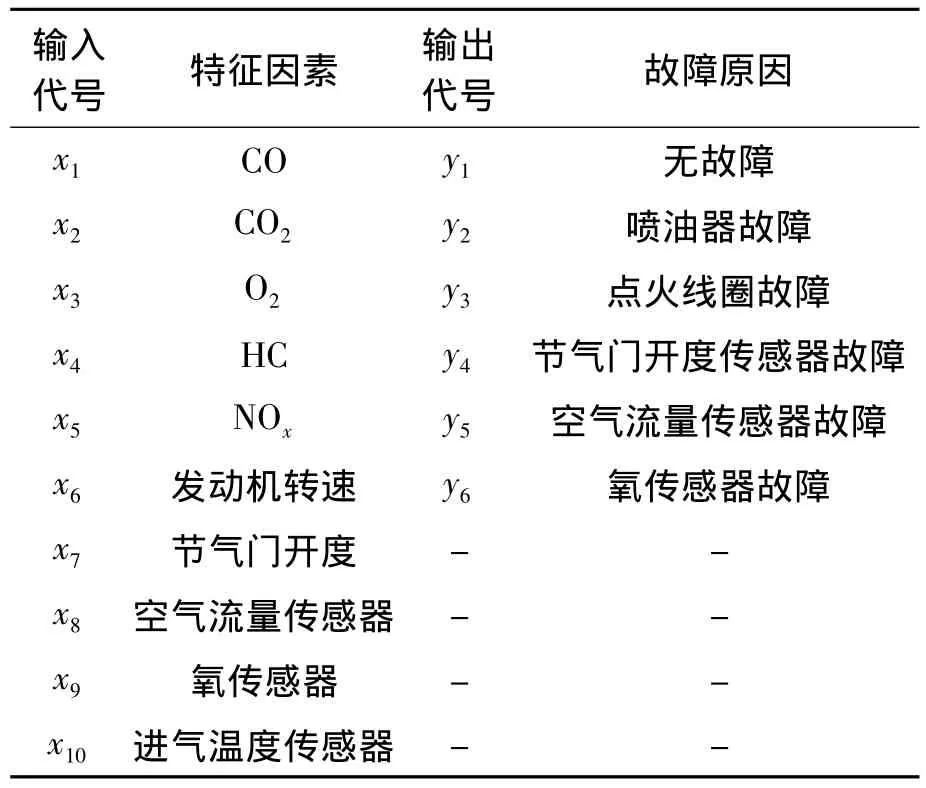
表2 故障特征因素及故障原因

以故障原因Y=(y1y2y3y4y5y6)T作为输出，y1，y2，y3，y4，y5，y6分别代表发动机无故障、喷油器故障、点火线圈故障、节气门开度传感器故障、空气流量传感器故障、氧传感器故障。输出节点数等于所能识别的故障类型数，所以取6个输出节点，相应的故障类型对应输出神经元的输出结果。以故障参数X=(x1x2x3x4x5x6x7x8x9x10)T作为样本输入，x1，x2，x3，x4，x5，x6，x7，x8，x9，x10分别代表 CO(10－2)，CO2(10－2)，O2(10－2)，HC(10－6)，NOx(10－6)含量和发动机转速、节气门开度、空气流量传感器、氧传感器、进气温度传感器的数值信号。以多组不同故障类型下的样本来训练所搭建的神经网络，从而建立起故障类型与故障模式之间的映射关系。

对于一般的模式识别及故障诊断问题［12］，3层BP神经网络就可以很好地解决。根据故障样本的特点，设置输人节点数为10，隐含层节点数为17，输出层节点数为6。建立BP神经网络，并且设定其歩长、目标、显示间隔、学习率等。用train函数来对网络进行训练，相应的训练语句如下:

程序运行完毕出现如图2所示的BP神经网络模型训练界面。

图2 BP神经网络模型训练界面

3 BP网络的故障诊断

为更好地提高数据的有效性，在无负荷怠速(800 r/min左右)和加速工况(1800 r/min左右)两种状态下，采集6种常见故障的多组各10个发动机的样本数据，从中随机选出两组(表3、4)。由于大部分相对于测量值比较大的波动会破坏神经网络的学习过程，使其不能反映小测量值变量的变化，而且网络是通过调整各层权值的大小来学习变量相对重要性的。若输入变量幅值相差太大，则网络完成学习时权值之间的大小相差很大，导致诊断结果偏差过大，所以对其样本数据进行归一化处理，所得数据如表5、6所示。

利用表5、6中已经归一化的数据样本进行训练。在训练函数trainglm的训练下其网络训练误差平方和随训练步数的变化曲线如图3所示。从图3(a)中可见:在怠速状态下，在模型训练迭代到第24步时，训练误差平方和为0.000057463，此时达到最小值;在加速状态下，迭代到第13步时，训练误差平方和为0.0000149。两者都在期望误差0.001范围内，且训练时间很短。这说明BP神经网络训练步数和训练时间少、收敛速度快，利用此神经网络能快速诊断出发动机故障。

利用己经训练好的神经网络权值，将采集的待诊断样本数据进行归一化处理，再输入到BP网络中进行仿真，以此来验证BP神经网络诊断故障的准确性。待诊断数据经归一化处理后见表7、8，其诊断结果如表9、10所示。

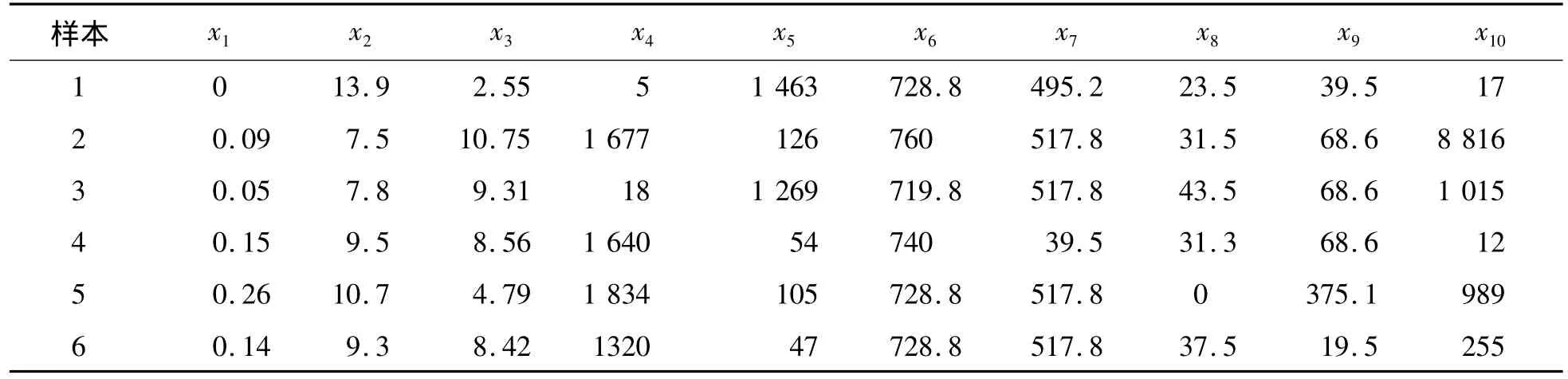
表3 怠速状态下的故障样本数据

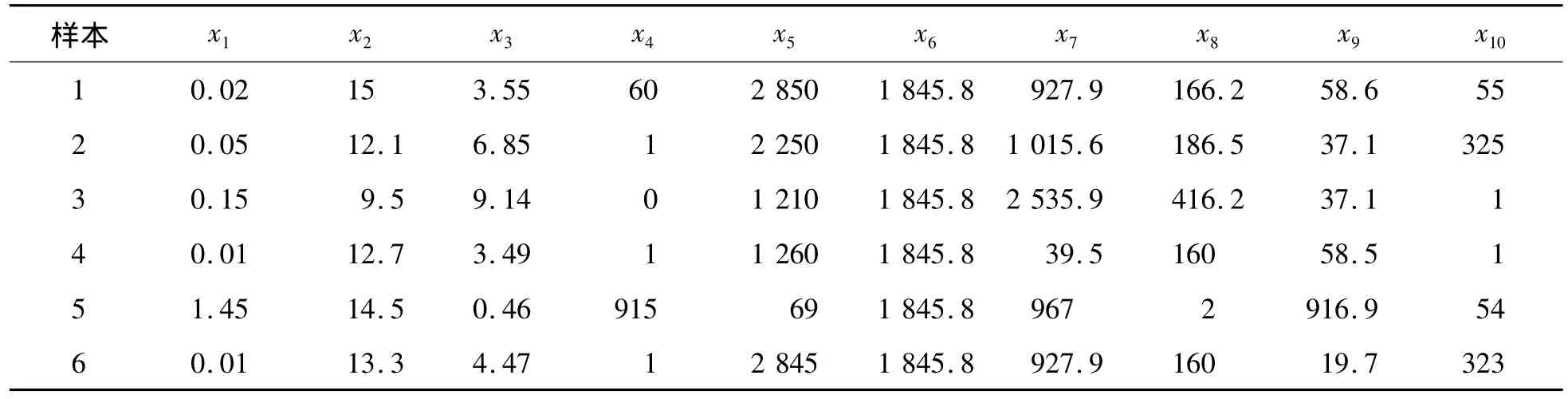
表4 加速状态下的故障样本数据

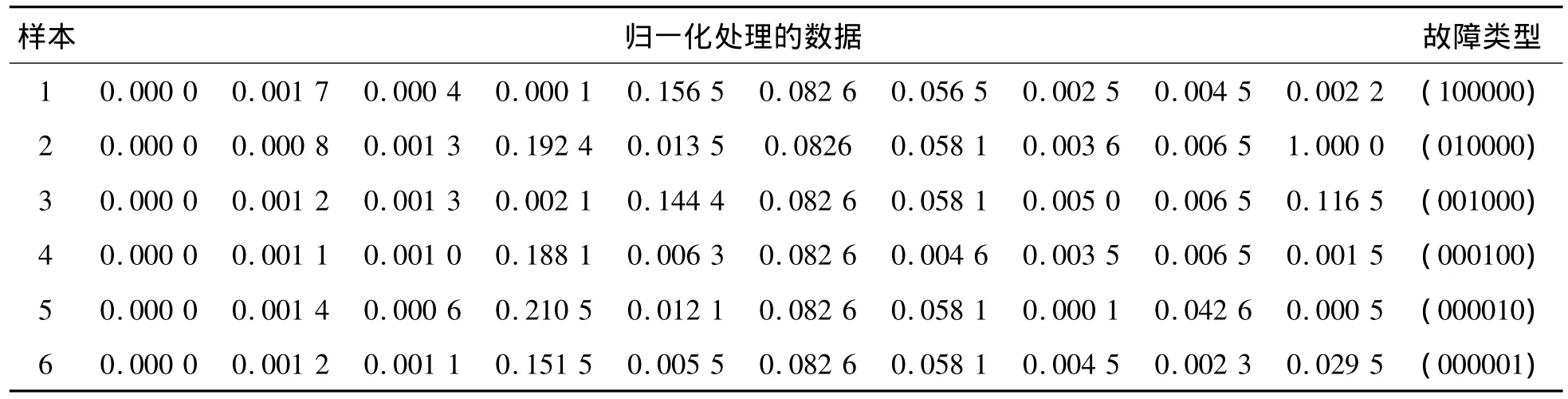
表5 怠速状态下的训练样本

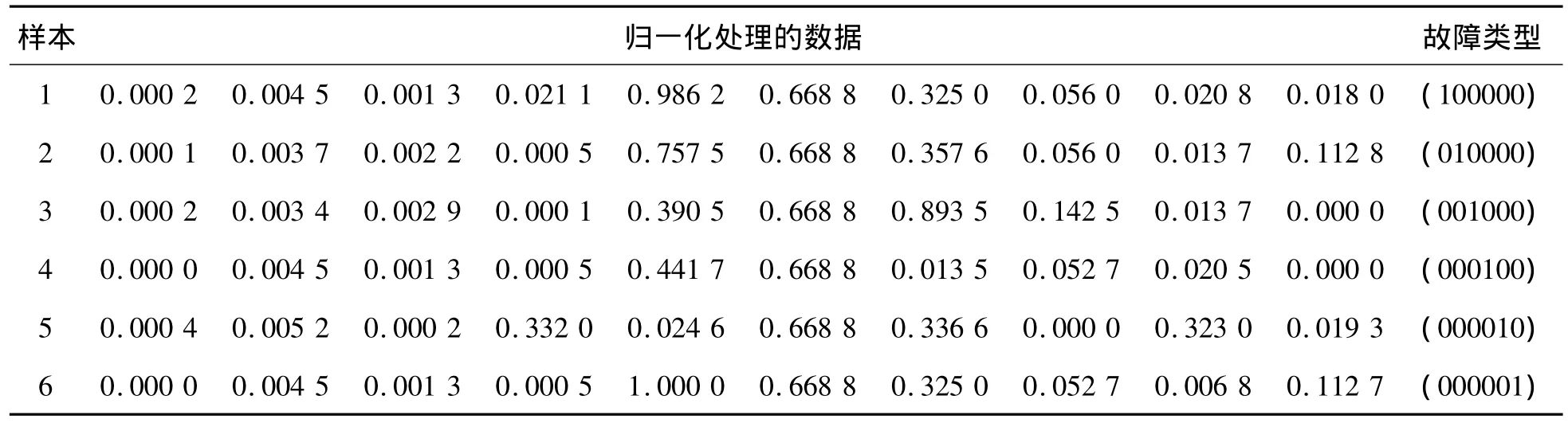
表6 加速状态下的训练样本

图3 BP神经网络训练误差平方和随训练步数的变化曲线

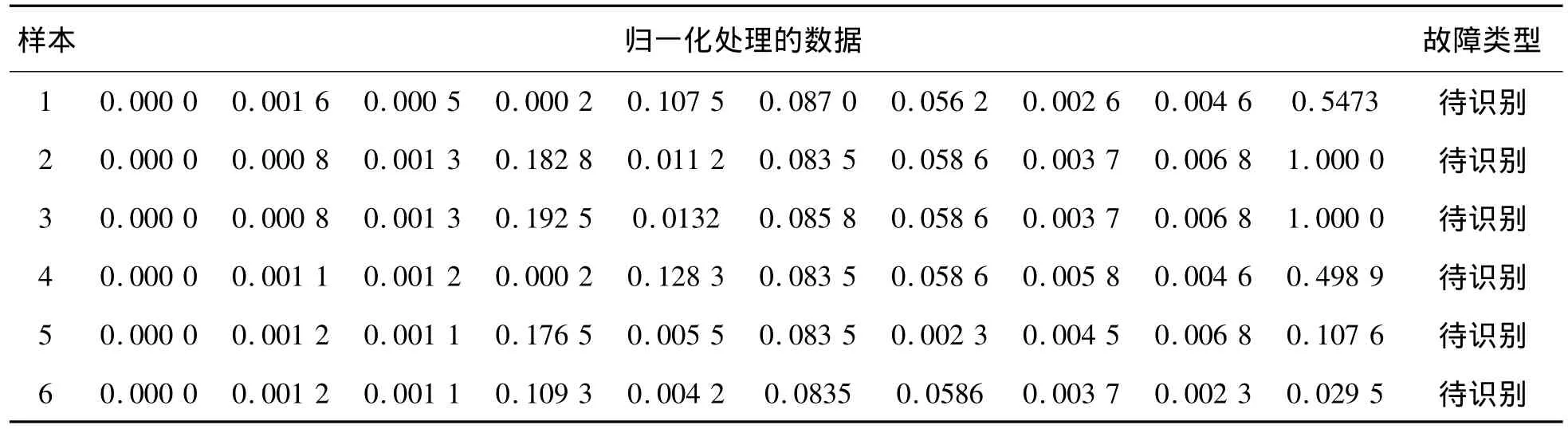
表7 怠速状态下验证数据

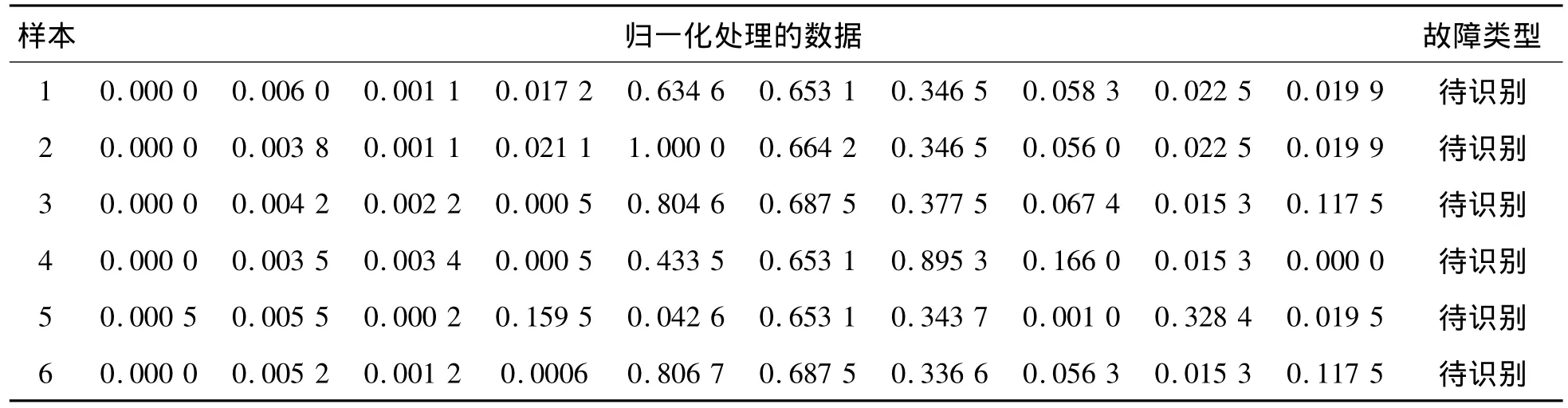
表8 加速状态下验证数据

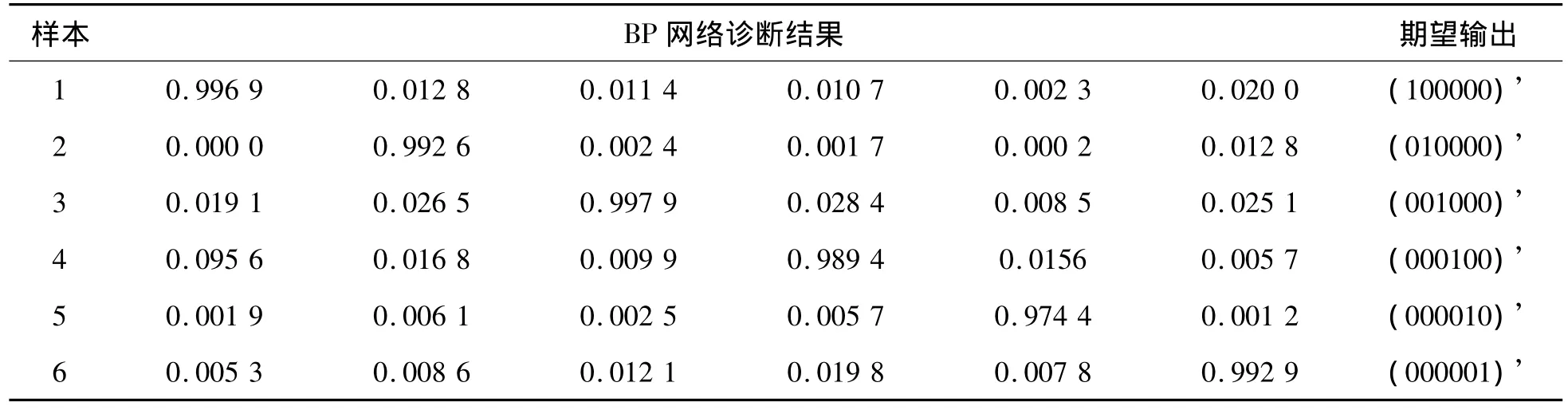
表9 验证诊断结果1

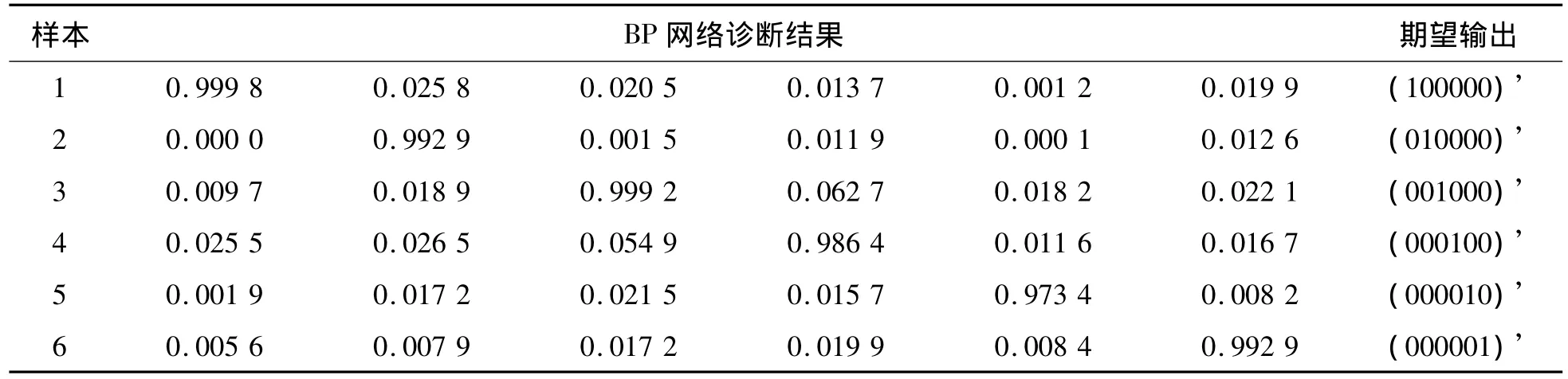
表10 验证诊断结果2

4 结论

1)对比怠速和加速两种状态下的验证诊断结果，实际输出值与期望输出值很接近，验证了所建神经网络模型的准确性及有效性。

2)通过训练后的BP神经网络能准确诊断电控发动机的故障，可进一步完善后将其理论运用到汽车尾气分析仪中，使分析仪不仅检测尾气参数，还可根据尾气值的数量关系判断发动机的相应故障，降低故障检测的劳动强度和成本，提高故障诊断效率。

［1］董长虹.Matlab神经网络与应用［M］.北京:国防工业出版社，2005.

［2］陈瑜，胡毅.基于BP神经网络的发动机故障诊断研究［J］.计算机应用技术，2008(1):81.

［3］李书明，黄燕晓，程关兵.应用BP神经网络方法的民航发动机故障诊断［J］.中国民航大学学报，2012，25(1):40.

［4］兰胜坤.遗传算法优化BP神经网络的说话人识别系统［J］.重庆理工大学学报:自然科学版，2013(10):91－95.

［5］钟宇平，王丽丹，段书凯，等.基于神经网络及强化学习的智能控制系统［J］.西南大学学报:自然科学版，2013(11):172－180.

［6］江雷，任德奎，张宁，等.BP神经网络在装备保障性评估中的应用［J］.四川兵工学报，2014(10):74－76.

［7］郑丹平，朱名日，刘文彬，等.基于BP神经网络的冷极射频消融凝固灶预测研究［J］.激光杂志，2014(11):95－97.

［8］郭阳明，冉从宝，姬昕禹，等.基于组合优化BP神经网络的模拟电路故障诊断［J］.西北工业大学学报，2013(1):44－48.

［9］罗学东，范新宇，代贞伟，等.BP神经网络模型在露天矿爆破振动参数预测中的应用及修正［J］.中南大学学报:自然科学版，2013(12):5019－5024.

［10］Jian-Ping Wang，Xiao-Min Li，Yong Hang.Motor failure diagnosis based on ant colony algorithm and BP neural network［M］.Noise:Vibration Worldwide，2011.

［11］肖云魁.汽车故障诊断学［M］.北京:北京理工大学出版社，2001.

［12］Kosmas Kosmidis，Antonios Stavropoulos.Corporate failure diagnosis in SMEs:A longitudinal analysis based on alternative prediction models［J］.International Journal of Accounting and Information Management，2014(6):221.