教育“无痕” 精彩“有迹”

徐 斌 江苏省特级教师，中学高级教师，江苏“人民教育家工程”培养对象，教育部“国培计划”首批特聘专家，人大复印资料《小学数学教与学》编委。

1992年获江苏省小学数学优质课比赛第一名，2000年获全国小学数学观摩课评比一等奖。曾应邀为全国第五届小学数学学术年会上观摩课，在《小学数学教师》等20余家刊物发表论文400余篇，应邀到全国20多个省、市、区讲学400余次。教育事迹在《人民教育》“名师人生”栏目作专题报道，《中国教育报》曾七次连载了“徐斌教育教学艺术系列报道”。出版专著《追寻无痕教育》《为学生的数学学习服务》《推敲新课程课堂》《另类课堂》及“中国名师”系列教学光盘。其教育主张是无痕教育，课堂教学风格稳健厚实。

无痕，从字面上讲，就是没有痕迹，不留印记，一切如初。“痕”本意是指创伤痊愈后留下的疤痕，也泛指斑迹。无痕，常被作为一种美学境界被众多文人墨客所描绘。贾岛《江亭晚望》：“鸟归沙有迹，帆过浪无痕。”苏轼《与潘郭二生出郊寻春》：“人似秋鸿来有信，事如春梦了无痕。”杜甫的《春夜喜雨》更是描绘了一幅无痕美景：“随风潜入夜，润物细无声。”

无痕被用于教育，早已有之。无痕教育，是指“把教育意图与目的隐蔽起来，通过间接、暗示或迂回的方式，给学生以教育的一种教育方式”（卢克谦《无痕教育：具有美学韵味的教育方式》）。无痕教育的提出，虽来源于德育领域，但其所彰显出来的人性化和科学性光辉，足可以指导一切学科教学行为。苏霍姆林斯基曾说，“造成教育青少年困难的最重要原因，在于把教育目的在学生面前以赤裸裸的形式进行”“把教育意图隐蔽起来，是教育艺术十分重要的因素之一”。杜威在论述什么是教育时指出：“一切教育都是通过个人参与人类的社会意识而进行的。这个过程几乎是出生时就在无意识中开始了。”“由于这种不知不觉的教育，个人便渐渐分享人类曾经积累下来的智慧和道德的财富。”无痕教育不仅是一种教育方式，更是一种教育思想，是一种教育心理学的规律和原则，是一种教育的美学和哲学境界，是一种对教育本原的追寻。

在小学数学教学中，如何实施“无痕教育呢”？笔者以“解决问题的策略”的教学为例，谈几点体会。

一、不知不觉中开始

让学生在不知不觉中开始学习，是无痕教育追寻的基本境界。不知不觉中开始，从教育心理学角度看，是确立合适的学习起点，即明确学生“现在在哪里”。有了对教学内容的整体把握，就有了对学生原有认知与学习状态的准确了解，就有了对学生生活经验与思维体验的适度掌握。有了这样的教学前提，就能够进一步明确把学生“将要带向哪里”以及“如何走向那里”，从而无痕地将学生引向新知的边缘，让学生对新知学习的需求油然而生。

【案例1】《解决问题的策略：一一列举》的课堂引入

师：请看，在我们日常生活当中，经常会遇到这样的现象——飞镖游戏，玩过吗？

生：玩过。

师：这是飞镖的靶子，如果让我们全班每人都来投一镖，大家有可能得多少环呢？

生：有可能是10环，8环，6环。

师：（相应板书）还有其他可能吗？

生：可能是0环。

师：对，可能连靶子都没有射上，那就是0环。

师：这些都是可能的结果，现在老师把它们都——

生：列举出来了。

师：说得很好！（板书：列举）列举就是一种策略，那刚才为什么要把它们列举出来呢？

生：我觉得应该是要知道它一共有多少种可能。

师：对，把每一种可能都列出来，那不是一般的列举，叫作一一列举。今天这堂课，我们就来学习一一列举的策略。

上述教学片段，从学生十分熟悉的飞镖游戏引入，从探索“每人都投一次，可能得多少环”这一问题入手，让学生从生活现象中发现数学问题，从而引出“一一列举”的策略。这样的新课引入，学生似乎在回忆生活经历，又似乎在体验游戏活动，又似乎在探寻数学规律，学生在不知不觉中自然地把生活经验与数学方法联系起来，从而生发出对一一列举策略的探究欲望。

可见，在课堂学习的起始阶段，从学生熟悉的生活问题出发，让学生捕捉数学信息，发现数学问题，提出数学问题，使学生了解知识的产生源头，能沟通起数学与生活的密切联系，为数学模型的建立打下现实基础。

二、潜移默化中理解

“教是为了更好地学。”对知识和方法的理解是学习的重要目标。小学阶段，儿童的认知水平处于皮亚杰指出的“具体运算思维”阶段，其最大特点是思维离不开具体事物的支持，这也导致小学生的感知觉、观察力和记忆均处于初步发展水平，其学习数学的动机和兴趣很不稳定。在这样的前提之下，儿童学习数学的过程，需要充分借助形象直观的教学手段，充分利用新旧知识的相互作用，以顺应儿童的学习心理，让儿童在不露痕迹中获得新知，在潜移默化中理解数学本质。

【案例2】《解决问题的策略：替换》的建模过程

例题：小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。小杯的容量是大杯的。小杯和大杯的容量各是多少毫升？

变式：小明把720毫升果汁倒入6个小杯和1个大杯，正好都倒满。大杯的容量比小杯多20毫升。小杯和大杯的容量各是多少毫升？

结合学生的探索逐步完成板书：

1+6720+620]

师：变式题与刚才的例题在解法上有什么不同？

生1：替换依据不同。例题中，两个数量是倍数关系；变式题中，两个数量是相差关系。

生2：替换后的总量不同。例题中，替换后总量还是720毫升；变式题中，替换之后的总量发生了变化，变多了或者变少了。

师：是啊！由于替换的依据不同，替换后的总量会不一样。如果我们观察替换前后杯子的个数，你有什么发现？

生1：倍数关系的替换，替换之后杯子的总个数变化了。

生2：相差关系的替换，替换之后杯子的总个数没有变化。

师：同学们观察得真仔细！数学就是这么奇妙！在变与不变中存在着内在的联系。

上述案例在帮助学生理解和建立替换策略的数学模型时，首先让学生分别探索和经历了倍数关系和相差关系的替换过程，然后对两种典型替换进行对比，使学生发现两种替换的异同点，并沟通起两种关系替换的内在联系，对替换策略的数学模型有深入的认识，促进学生良好认知结构的形成。这样的学习过程，不是把解题策略灌输和传递给学生，而是让学生动手实践与自主探索、观察对比与联系内化，在潜移默化中理解替换策略的本质，并对两种典型的替换类型有深刻的认识。

可见，学生建立数学模型的过程，一方面需要让学生运用数学语言和符号分析问题，另一方面也需要让学生在建立数学模型的同时获得结构化的理解。因此，数学模型的建立过程，需要让学生充分经历、体验和探索，在潜移默化中获得对模型丰富性和深刻性的认识。

三、循序渐进中掌握

学生学习数学的过程，既是在教师引导下的意义建构过程，也是在自身需求发展中的自主建构过程。无痕教育视野下的学生数学学习过程，更主要地体现为教师精心设计学生的学习进程，从某种意义上说是一种“进”与“退”的艺术。通过适当的“退”和必要的“进”，能使学习过程成为学生潜移默化地掌握知识和技能的过程。在课堂上，“进”“退”之间体现的是一种行云流水般的从容节奏，是一种水乳交融般的无痕状态。

【案例3】《解决问题的策略：画图》的练习片段

原题——“张庄小学原来有一个长方形操场，长50米，宽40米。”让学生首先在脑中画图，然后逐步变化条件和问题，不断让学生脑中画图猜测，并在纸上画图验证结果。

变式之一：“在修建时，长增加8米，面积增加多少平方米？”学生很快在脑中画图，甚至不需要在纸上画图，即可用手势比划出图像（图1），并列出算式40×8=320（平方米）。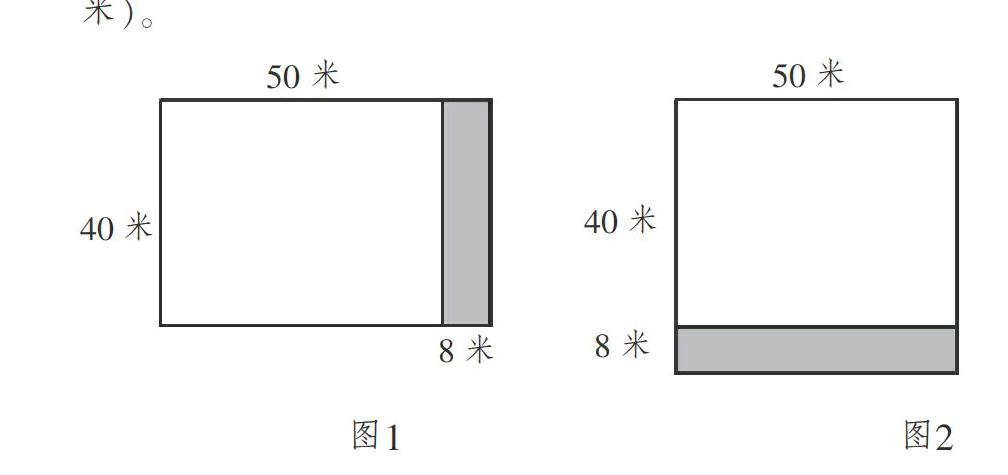

变式之二：“在修建时，宽增加8米，面积增加多少平方米？”有了前面的经验，学生更加熟练地脑中画图（图2），并列式解决问题50×8=400（平方米）。

变式之三：“在修建时，长和宽各增加8米，变成新的长方形。面积增加多少平方米？”老师刚出示完题目，不少学生即快速抢答：“面积增加720平方米，列式是320+400=720。”

在学生画图列式之后，教师再次提出：经过头脑里画图猜想和在纸上画图验证，大家发现面积增加的部分是720平方米吗？这是什么缘故呢？同时结合学生的画图进行展示和解释，从而突破学习难点（从图3逐渐演变为图5）。 有了以上三次变式，学生积极性高涨，对画图策略的探索兴趣更浓，教师继续出示了以下三次变式：

变式之四——“修建时，长和宽各减少8米，操场的面积减少多少平方米？”

变式之五——“修建时，长增加8米，宽减少8米，面积改变吗？为什么？”

变式之六——“修建时，长减少8米，宽增加8米，面积改变吗？为什么？”

以上教学设计和组织，让学生边画图边思考，边猜测边验证，边对比边讨论，不断发展学生的几何直观水平，使学生不断体验到画图策略的价值所在。这种一题多变的方式，紧紧围绕画图策略，让学生不断猜测、验证、联想、推理，经历不同情形下的数形变化过程，探究图形变化中的内在规律，引导学生在数学思维活动中逐步积累数学活动经验，让学生在运用画图策略解决实际问题的过程中深入探索变化规律，享受数学思维活动的快乐。

可见，“进”与“退”的过程，是学生潜移默化地掌握知识技能的过程，是学生不露痕迹中培养思维能力的过程，是学生淡墨无痕中发展数学思维的过程。从这个意义上说，数学教学的智慧就在于教师能在“进”与“退”之间游刃有余。

四、春风化雨中提升

课堂是师生人生中一段重要的生命经历，课堂是充满无限魅力的地方，课堂是学生充分发展的天空。无痕教育理念指导下的数学课堂，是学生享受教师服务的过程，也是学生自主学习、主动发展的过程。这样的过程，学生的学习经历应是充实快乐的，学习结果是充分有效的，学习过程是充满智慧的。理想的课堂教学过程，似雪落春泥，悄然入土，孕育和滋润着生命。虽无痕，却有声有色，有滋有味；虽无痕，却如歌如乐，如诗如画。

【案例4】《解决问题的策略：转化》的新知展开

（1）回顾公式推导的经历。

启发思考：其实，在我们小学阶段的数学学习中，比如说一些图形面积公式、体积公式的推导，就常常用到转化的策略，你们能想起来吗？

反馈交流（根据学生的回答，课件相机呈现公式的推导过程）。

（2）感受转化策略的作用。

回顾：我们在推导平行四边形、三角形和梯形的面积计算公式时，是先知道哪个图形的面积计算公式的？接下来我们是如何研究图形之间的面积关系的？我们又是把哪些图形转化成平行四边形（三角形、梯形）的？长方体、圆柱和圆锥的体积计算公式呢？

感受：在刚才应用转化策略推导出这些公式时，你们发现它们都有什么共同的特点？（转化前这些问题都是我们面临的新问题，而我们都是把它转化成曾经学习过的旧知识。）

（3）拓展转化策略的应用。

想一想：在学习认数和计算时，哪些地方用到过转化的策略呢？

练一练：计算+++。

提问：你能运用转化的策略来解决这一问题吗？

上述案例中，主要从三个层面让学生经历转化策略的形成过程：（1）图形面积、体积方面的应用；（2）图形周长、内角和方面的应用；（3）数与计算方面的应用。在转化策略的形成过程中，遵循学生的心理规律，逐步深入展开，首先让学生经历直观的单一图形的转化，接着让学生经历形与形之间的转化，然后再让学生经历数与计算方面的转化。不同层面的转化策略，思维含量是不一样的，分类让学生经历转化策略的形成过程，符合学生“感知—表象—抽象”的认知规律。

可见，建立数学模型之后，为了让学生对初建模型有充分的感性积累，应该让学生运用数学模型解决同类数学问题，在解决数学问题的过程中，积累数学活动经验，获得对数学模型的深刻理解，形成初步运用数学模型的相关技能，提升学生的数学思想，培养学生的数学素养，为进一步解决实际问题打下坚实基础。?