十字交叉法错误题分析

吴孙富+肖柏林

摘要：从数学的角度探讨了用十字交叉法解题导致增解和漏解的原因，指出错解某例题是由于解题者错误地使用了氢碳原子个数比，进一步分析证明错解的深层次原因在于该题使用的数据有问题。强调题目编制过程中应重视科学性，尤其要注意错题在教学中的破坏作用。

关键词：化学计算；十字交叉法；二元一次方程组法；氢碳比

文章编号：1005–6629（2015）6–0080–04 中图分类号：G633.8 文献标识码：B

1 问题的提出

李薇老师原创了一道例题（下文所说例题均指此题）如下：

相邻两种烷烃的混合物20mL，完全燃烧后生成30mL的CO2，48mL的H2O。求该烷烃的可能组合及体积比。

在“十字交叉法应用中的常见问题及解析”[1]一文中，李薇老师先求出了混合烃的平均分子式为C1.5H4.8，再根据C1.5H4.8确定两种烷烃为CH4和C2H6，然后用氢碳比的十字交叉法进行求解得甲烷与乙烷的体积比为1：2（具体解法请参看文献[2]和下文）。

在“对一道错题的剖析——兼析十字交叉法的应用”[3]一文中，万辉霞和钟辉生两位老师用二元一次方程组解答了此例题。两位老师在求出平均分子式为C1.5H4.8、确定例题中两种烷烃分别为CH4和C2H6之后，根据混合烃的体积与CO2的体积、混合烃的体积与H2O的体积分别列出了两组二元一次方程组进行求解。两位老师先用两组二元一次方程组解出两组甲烷与乙烷的体积，然后再将两组体积分别求比值得两组体积比分别为1：1和3：2（具体解法可参看文献[4]和下文）。由于两组方程组的求解结果不同，所以两位老师得出了例题无解、例题是错题的结论，笔者赞同该结论。

例题无解，但李薇老师用十字交叉法所求例题的解为1：2。由于李薇老师用十字交叉法所求的解为错解，所以万、钟二位老师将李薇老师得出错解的原因归咎于十字交叉法。笔者认为，李老师得出错解的原因不在于十字交叉法，而在于例题本身提供的数据不科学。

2 十字交叉法的“增解”和“漏解”

2.1 十字交叉法及其在数学上的“增解”和“漏解”

万、钟两位老师之所以将李薇老师对例题的错解归咎于十字交叉法，是因为两位老师认为李老师的错解是用十字交叉法解题导致的增解。在此，笔者特先探讨一下十字交叉法的“增解”和“漏解”问题。

由此可见，C1.5H4.8是一个鸡鸭的总个数与总脚数不相匹配的组成，C1.5H4.8不能代表任何以比例组成的甲烷和乙烷混合物。从主观上说，李薇老师错解例题的原因在于使用了氢碳比；从客观上说，由于C1.5H4.8中的数据源于题给的数据，所以李薇老师错解例题的客观原因在于题目本身的数据不科学。

上述探讨还给我们这样一个重要的启示：在涉及分子式或化学式中原子个数的计算时，我们要慎用原子个数的比值。

4 例题存在的问题及相关的教学反思

4.1 例题存在的两个问题

由上述探讨可见，例题存在的第一个问题是数据不科学。实际上在“相邻两种烷烃”的前提下，例题只需要提供混合烃的总体积和二氧化碳的体积就可以求解，例题如果只提供混合烃的总体积和水的体积也可以求解（可参看文献[1，3]及笔者的上述解法）。当然，例题亦可以同时提供混合烃的总体积、二氧化碳和水的体积，只是在同时提供三者的体积时必须考虑各体积间的科学匹配性。当例题同时提供科学匹配的各物质的体积时，李老师与万、钟两位老师及笔者的上述解法就会得出一致的结论，且各解法的结果之间可以相互验证。对于平均组成为C5/3H16/3的甲烷和乙烷混合物来说，用各解法所求的结果均是n（CH4）：n（C2H6）=1：2。

例题存在的第二个问题是完全忽视了反应条件与物质状态间的关系。题目在没有任何反应条件的前提下，给出了混合烃、二氧化碳和水的体积，几位老师解题时都毫不犹豫地把混合烃和水当成了气态进行解答。大家都知道物质状态与外界条件是密切相关的，可这几位老师在编题和解题时都完全忽视了外界条件，这充分反映出了在教学中只追求结果、不顾及科学逻辑的缺点。这个缺点应该引起广大中学化学教师的高度重视。

4.2 关于例题的教学反思

在存在上述两个问题的情况下，如果不加思考地把此例题作为训练题交给学生解答的话，将会出现些什么情况呢？笔者预计会有三种情况。一种情况是部分优秀的学生可能会感到难以下手，因为他们在解题时首先会考虑到混合烃和水的状态，不明确混合烃和水的状态，就难以解答此题。当这些学生对此提出疑问时，会不会有教师武断地肯定混合烃和水为气态呢？笔者不敢肯定说“没有”。第二种情况是部分学生把混合烃和水都当成气态进行解答，在解题思路和运算过程均正确的情况下，学生可能会得出三种互不相同的结果。当三种结果呈现在教师面前时，会不会有教师武断地否定其中的两个结果或者束手无策呢？笔者亦不敢肯定说“没有”。第三种情况是有学生经过讨论解答后得出“题目错误”或“此题无解”的结论，会不会有教师因毫无准备而敷衍了事呢？笔者亦不敢肯定说“没有”。

想想这些可能的情况，我们自然就会明白这样一个道理：一道化学错题对于我们化学教学既可能是很好的机会和挑战，也可能产生很大的破坏作用。为了避免此种破坏作用，我们应该认真地、科学地编写每一道原创题。我们还应该深入地研究包括错题在内的例题和习题，灵活科学地应对教学中出现的科学问题，改善我们的教学。

我们可不可以把这样一道错题变成好题呢？完全可以，笔者研究后把例题改编成了如下选择题。

在110℃、1大气压下，相邻两种气态烷烃的混合物20mL，完全燃烧后恢复到原温度和压强，测得CO2的体积为30mL、H2O的体积为48mL。该混合烃的可能组成为（ ）。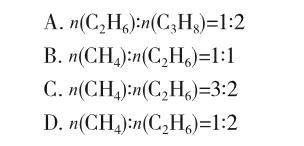

E.无解

改变后的选择题既可以起到巩固学生基础知识、提升学生基本技能的作用，又可以起到发散学生思维、启发学生探究的作用。相比之下，此题由错题变化而来，其教学价值远高于普通的训练题。

参考文献：

[1][2]李薇.十字交叉法应用中的常见问题及解析[J].化学教学，2012，（5）：65.

[3][4]万辉霞，钟辉生.对一道错题的剖析——兼谈十字交叉法的应用[J].化学教学，2013，（3）：78～79.