吉布斯效应在信号处理课程教学中的仿真分析
王凤随 王冠凌 瞿成明 赵 发
安徽工程大学电气工程学院 安徽芜湖 241000
吉布斯效应在信号处理课程教学中的仿真分析
王凤随 王冠凌 瞿成明 赵 发
安徽工程大学电气工程学院 安徽芜湖 241000
为帮助学生更直观地理解信号处理中出现的吉布斯效应,借助于计算分析软件MATLAB对信号处理中的信号分解与合成以及滤波器设计中出现的吉布斯现象进行了仿真,分析并探讨了吉布斯效应产生的原因及减少效应影响的方法。仿真结果可更加直观和深刻地认识吉布斯效应,对信号分析与系统设计有着重要的作用。
吉布斯效应;信号合成;滤波器;仿真分析
MATLAB是一种高性能的科学计算和可视化软件,它具有使用方便,运算高效,功能丰富,界面友好等诸多优点,已成为教学和科研中不可或缺的工具。其完备的信号处理能力及丰富的应用工具箱,使其在电子信息类课程教学中被频繁地应用。
在信号处理类课程中,信号的分解与合成以及设计滤波器不可避免地会受到吉布斯(Gibbs)效应的影响,在通常的教学中,仅对其进行理论分析与推导,只给学生一个抽象的印象,不能直观而形象地看到该现象的形成过程。基于MATLAB分析软件对信号处理中的吉布斯效应进行仿真,改变了传统的教学模式,实现了该效应的动态分析与可视化,有助于学生理解吉布斯效应的产生。
1 吉布斯效应
1.1 吉布斯效应的定义
任何非正弦的周期信号在满足一定条件时,都可以展开成为一系列不同频率的正弦信号。反之,可将不同频率的各次谐波进行合成得到该周期信号。在对具有跳变点的周期信号进行傅里叶级数展开时,如果仅选取无穷级数中的有限项合成原周期信号,那么在周期信号的不可导点位置将出现较大的误差(峰起)[1]。当选取的项数越多,在所合成的波形中出现的峰起越靠近原信号的不连续点。当选取的项数很大时,该峰起值趋于一个常数,大约等于总跳变值的9%,这种现象称为吉布斯效应。
1.2 吉布斯效应的实例
(1)周期信号的合成与分解
周期信号在满足狄利克雷条件时,可分解为直流和不同频率的正弦信号分量之和。若f(t)的周期为T1,角频率ω1=2π/T1,频率f1=1/T1,则周期函数f(t)的傅里叶级数如式(1)所示:
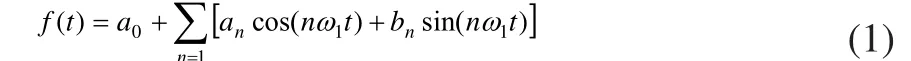
若取傅里叶级数的前2N+1项来逼近周期函数f(t),则傅里叶级数如式(2):

这样通过有限项傅里叶级数的和来逼近原信号,必然存在误差。通过计算机仿真实验,改变谐波分量的项数,可以演示信号分析中的吉布斯现象[2,3,4]。
(2)FIR滤波器设计
在利用窗函数设计FIR滤波器时,由于用有限长的序列代替无限长单位取样序列,这种截断近似势必带来误差,表现在频域就是Gibbs效应,这种吉布斯效应是由于对单位取样序列直接截断所引起的[5]。在频谱跳变点所产生的泄漏效应致使主瓣能量的丢失,使低频段出现了高频段的滤波结果。这种效应会引起通带内和阻带内的波动性,尤其是使阻带的衰减变小,从而导致技术实现上的困难。
2 吉布斯效应的仿真
2.1 周期信号的合成
不失一般性,以周期性方波为例进行说明,设周期T=2π,幅度为1,具有奇对称特性,其傅里叶级数展开式为:
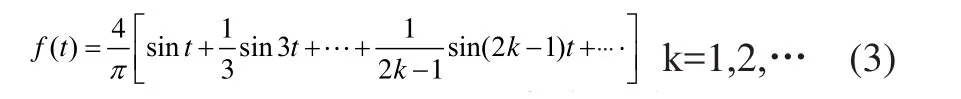
利用MATLAB语言编写程序实现各次谐波合成情况,从而演示吉布斯效应。k分别取1,2,3,5,10,50项,其仿真结果如图1所示。
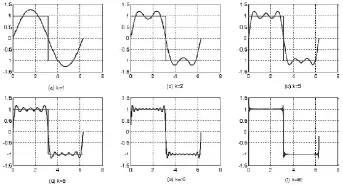
图1 周期方波吉布斯效应仿真结果
从仿真结果不难看成,周期方波合成时有如下显著特点:(1)随着所取项数的增加,合成的波形越逼近原始方波信号。(2)当所取项数增大时,合成波形的峰起向方波间断点靠近,然而峰起值并未明显减小,峰起所包围的面积减少,MATLAB仿真可清楚地展现此Gibbs效应。(3)信号的低频分量对应的幅度较大,在方波中居主体地位,主要影响波形的顶部;信号的高频分量对应的幅度偏小,主要对波形的细节和跳变沿影响较大。
2.2 FIR滤波器设计
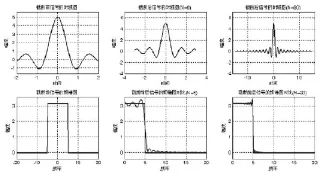
图2 滤波器设计中吉布斯效应的仿真结果
通过MATLAB获取峰起点坐标可以计算出:当N=6时,峰起总跳变幅度为(3.411-3.142)/3.142=8.56%,第一峰起到间断点的距离4.913-4.091=0.822;当N=30时,峰起总跳变幅度为(3.423-3.142)/3.142=8.94%,第一峰起到间断点的距离4.913-4.751=0.162。
从仿真结果可以看出:(1)窗函数长度N越大,通带和阻带内波动越快。(2)加大窗函数长度,可以使滤波器过渡带变窄,但带内波动幅度并没有明显改善,加大N并非减少Gibbs效应的有效方法。(3)减少吉布斯效应影响的方法只能从窗函数的形状角度考虑,如选择能量更加集中的升余弦窗,然而这样做通常要牺牲过渡带宽度为代价。减小过渡带宽度和增大阻滞衰减是一对矛盾,一般很难同时得到满足,在实际的滤波器设计中,通常根据技术指标在二者之间折中。
3 结束语
通过对信号处理中吉布斯现象的仿真分析,将抽象的现象变得具体而直观,使学生很容易理解吉布斯效应的成因及抑制措施,提高了学生对课程学习的积极性。计算机软件辅助教学是科学技术发展的必然结果,可实现系统的可视化,有助于提高教学质量,是值得大力推广的一种教学模式。
[1] 吴大正,杨林耀.信号与线性系统分析[M].第4版.北京:高等教育出版社,2005.
[2] 王怀兴.基于LabVIEW的周期信号分解与合成实验研究[J].湖北第二师范学院学报,2010,27(8):52-53.
[3] 郝艳华.基于Matlab周期信号的分解与合成[J].计算机与现代化,2011(9):156-158.
[4] 王宏伟,张文凯.MATLAB在信号分解与合成实验教学中的应用[J].科技创新导报,2013(22):165-166.
[5] 高西全,丁玉美.数字信号处理[M].第3版.西安:西安电子科技大学出版社,2008.
Simulation Analysis of Gibbs Effects in the Course Teaching for Signal Processing
Wang Fengsui, Wang Guanling, Qu Chengming, Zhao Fa
Anhui Polytechnic University, Wuhu, 241000, China
In order to help the students intuitively understand Gibbs effects in signal processing, Gibbs effects appearing in signal decomposition and synthesis and filter design for signal processing were simulated by using MATLAB analysis software. The cause of Gibbs effects was analyzed and the methods for reducing the influence of Gibbs effects were discussed. Simulation results are able to more intuitively and profoundly understand the Gibbs effects. It plays an important role for signal analysis and system design.
Gibbs effects; signal synthesis; filter; simulation analysis
2014-07-16
王凤随,博士,讲师。
安徽工程大学引进人才科研启动基金(编号:2014YQQ006);安徽省高等学校教学研究项目(编号:2012jyxm275);安徽工程大学校级电子信息类专业拔尖人才培养模式创新实验区项目、安徽工程大学2010电子信息工程校级特色专业建设项目。

