减小投影长度变形值方法的研究

韩 冬

（锦州铁道勘察设计院有限公司，辽宁 锦州 121000）

随着时代的进步，对测量的技术标准提出了更高的要求，很多测量规范中都对平面控制网的坐标系统投影变形提出了不大于25mm/km的要求，而我国高铁更是提出了投影变形值不大于10mm/km的要求，而国家统一的3度带高斯正行投影平面直角坐标系存在较大的边长投影变形，在投影边缘地带投影变形值达到了340mm/km，这导致在采用坐标测量定位方法进行施工测量时，由坐标反算的边长值与现场实测值每公里有340mm的误差值，远远不能满足工程建设的要求。因此合理的设计选定坐标系，有效的控制投影变形对工程建设的影响，是保证设计、施工的顺利实施和工程质量的重要前提。

1 投影变形

众所周知，地图是平面的，而我们测量的元素是在地球椭球面上的，也就是说地球椭球面上诸元素必须通过数学方法投影到某个平面，以实现地图投影。由于地球椭球面是不可展曲面，为使不产生裂口和重复，不论采用哪种常规投影方式，必然会产生一定的投影变形。

测量是在地面上进行的，而大地计算是在参考椭球面上进行的，因此，必须把地面上的观测值换算到参考椭球面上，然后再从参考椭球面上投影到平面上，所以投影变形主要包括两部分：

（1）地面换算至参考椭球面，即高程归化变形。

（2）参考椭球面投影到高斯平面，即高斯正行投影变形。

1.1 高程归化变形

实测边长归化至参考椭球面上时，近似关系式为：

式中：

D——归算边的长度；

H——归算边高出参考椭球的平均高程；

R——归算边方向参考椭球法截弧的曲率半径。

由式（1）中看出△D总为负值，这表明地面观测长度归化到参考椭球面总是变短的，而且变形值与归算边高出参考椭球的平均高程成正比。

1.2 高斯正行投影变形

参考椭球面长度归化归化至高斯平面上的长度变形关系式为：

式中：

ym——归算边两端点横坐标平均值；

R——参考椭球面在归算边中点的平均曲率半径。

由式（2）中看出△D总为正值，这表明参考椭球面上的长度归化至高斯平面上总是变长的，而且变形值与横坐标平均值的平方成正比。

1.3 投影变形综合分析

通过以上分析表明，投影变形主要由两部分组成，因此长度综合变形值为

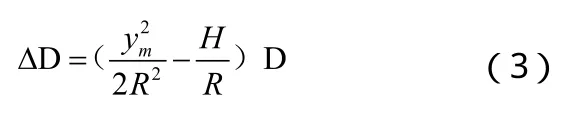
由式（3）中我们可以看出，高程归化投影变形与高斯正行投影变形符号相反，所以在一定区域内，两种变形可以相互抵偿。

2 减小投影变形值的方法

2.1 选择适当的投影面

不改变测区的中央经线，而是针对测区的平均高程，选择合适的高程参考面作为抵偿投影面，使得在该高程参考面上，高程归化投影变形抵消高斯正行投影的变形。

令△D =0，由式3可求得

该方法的优点是不改变国家统一的高斯正行投影的中央子午线，缺点是测区高程变化较大的地区，使用统一的参考面，不能使所有的地区投影变形都能满足要求。

2.2 选择适当的中央经线

不改变测区的高程投影面，而是对中央经线作适当移动，以抵消高程归化投影变形。

令△D =0，由式3可求得

该方法的优点是不改变归化高程面，只改变测区的中央经线，缺点是在东西走向跨越较大的测区往往很难令投影变形满足要求。

2.3 选择适当的投影面和中央经线

通过既改变测区的高程参考面，又移动中央经线来抵消两项投影变形。

令D=0，即

如果测区基本为东西走向，肯定不能采用国家统一的高斯正行投影3度带平面直角坐标系，单独的使用前两种方法也满足不了要求，这时，则可以采用本方法，同时改变测区的高程参考面和移动中央经线，选择中央子午线为经度的整度数，带宽取1度，其高程投影面选在设计高程以下，中央子午线附近不低于159米，边缘地区在59~376m范围内，二者共有范围为59~159m。这样不论在中央子午线附近，或者在中央子午线边缘，其投影变形都能满足要求。在实际应用时，1度带宽往往不能覆盖测区，这时，需要设立第二坐标系甚至第三坐标系，相邻坐标系应设置10km的重叠区，以保证设计及施工的顺利进行。

显然，这种方法综合了前两种方法的长处，这种坐标系能更有效、更灵活的实现两种投影变形的抵偿。

结语

随着各种工程项目对勘测设计和施工放样的精度要求越来越严格，对投影变形的要求越来越高，因此对坐标系统的选择显得尤为重要。本文对投影变形的产生及解决方法提出了几种方法，具有一定的实际意义。但是，我们通过这种方法求得的坐标可能与当地坐标存在一定的间隙，工程项目与外部衔接的时候应引起注意

[1]孔祥元，郭际明，刘宗泉.大地测量学[M].武汉：武汉大学出版社，2001.

[2]高成发. GPS测量[M].北京：人民交通出版社，2000.

[3]TB10101-2009，铁路工程测量规范[S].