双kicked棘轮模型中粒子香农熵演化的研究

陈 磊，肖 进，赵 宇，杜文汉

（常州工学院 电气与光电工程学院，江苏 常州 213002）

双kicked棘轮模型中粒子香农熵演化的研究

陈 磊，肖 进，赵 宇，杜文汉

（常州工学院 电气与光电工程学院，江苏 常州 213002）

Delta-kicked模型是可以实现棘轮效应的哈密顿型量子模型。在双kicked型棘轮模型中，2个频率不同的闪烁势交替作用于1个具有均匀零动量初态的粒子，在量子共振被激发的条件下，模型中便出现棘轮效应。在不同的量子共振下，粒子香农熵演化出现了不同的规律。研究表明从香农熵演化的角度分析，可以更好地判断量子共振是否被激发。

双kicked棘轮模型；量子共振；香农熵

1　双kicked棘轮模型研究背景

棘轮效应是很有趣的现象，它是指在没有平均定向力的作用下出现了粒子的定向运动。这个效应源于人们试图从热涨落里提取能量做功［1］。棘轮效应在许多技术和器件领域里都有着重要的潜在应用价值，例如整流器、电子泵、分子开关、粒子分离器件以及其他微观和介观输运器件［2］。费曼的思维实验［3］表明，由于热力学第二定律的限制，棘轮效应不可能出现在热平衡系统中。因此为了实现棘轮效应，就要通过额外的扰动来打破系统的热平衡状态。另外，系统的对称性会阻止定向粒子流的出现，所以系统的对称性也要被破坏［4-5］。满足条件的棘轮模型有很多种类型，早期的棘轮模型中噪声是必要因素，后来陆续出现了许多不含噪声的棘轮模型，如耗散混沌动力学型棘轮模型、纯哈密顿型棘轮模型。

棘轮效应在量子领域同样存在。例如利用光晶格可以很容易地在实验上实现量子势（quantum delta-kicked势，QDK势），基于QDK势的量子棘轮模型已经有所研究［6-7］。在这个模型中，1个双频非对称光晶格周期性地作用于1个粒子。当量子共振发生时（有效普朗克常数取一些特殊值），可以出现定向的粒子流动，即棘轮效应。此外，利用2个单频的闪烁势周期性交替作用于具有对称初态的粒子也可以实现棘轮效应［8］。这个模型就是双kicked模型。熵是对系统混乱度（无序度）的度量。通常系统在演化时，其熵值总是要增加的，这就是著名的熵增加原理。在研究双kicked模型中粒子在波数空间中的香农熵演化规律时，我们发现粒子香农熵的演化特征，与量子共振是否被激发以及棘轮效应是否出现有着密切的联系。以下介绍了几种不同的量子共振条件下，粒子香农熵演化的具体规律，并给出了相应的理论解释。

2　粒子香农熵演化的具体规律

双kicked棘轮模型的含义：原先的双频棘轮势sin （x）+αsin（2x）被替换为2个单频势sin（x）和sin（2x），这2个势交替作用于粒子。该模型中粒子遵从的薛定谔方程为：

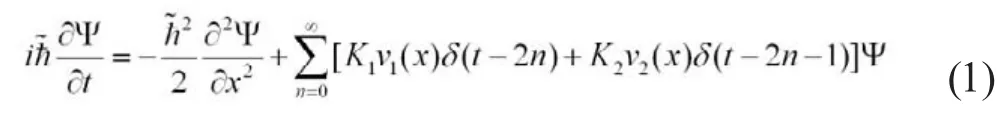
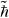
在双kicked模型中，系统的时间周期变为原先的QDK模型［6］时间周期的2倍。粒子态矢量的演化过程可以描述为：

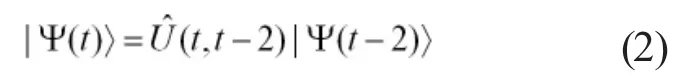
这里

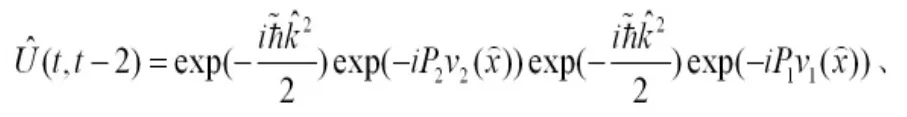
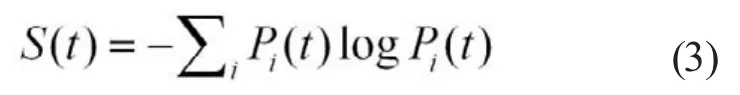
理论上求和指标i是有无穷多个的，但在实际计算中取有限项，只要求和项的数目大到一定程度即可。在实际计算中我们还会用n替换t，只计算在一些离散的时刻粒子香农熵的值，并进而分析粒子香农熵演化的规律。另外粒子的初态设为零动量态。

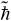
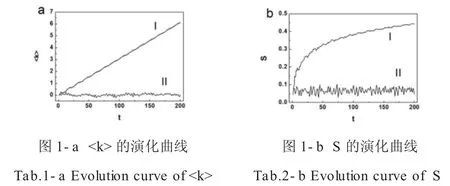
图1　双kicked模型中粒子的与S随时间演化的曲线

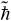
图2　4种量子共振被激发的条件下，双kicked模型中粒子的与S随时间演化的曲线

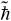
3　结论

本文对双kicked模型中粒子香农熵的演化进行了描述和分析。在这个模型中，2个闪烁势以等时间间隔的形式交替作用于初态为零动量态的粒子。在量子共振被激发的条件下，棘轮效应出现，同时粒子香农熵的演化比较剧烈。通过对几种不同的量子共振条件下，棘轮效应的特征以及粒子香农熵演化特征的分析，我们发现相对于从棘轮效应是否发生的角度分析，从粒子香农熵演化的角度，可以更全面地对量子共振是否被激发进行判断。

［1］ VON SMOLUCHOWSKI M.,Experimentell nachweisbare,der üblichen Thermodynamik widersprechende Molekular ph？nomene［J］.Physik.Zeitschr. 1912,（13）：1069-1080.

［2］ H？GGI P.,MARCHESONI F.,Artificial Brownian motors：Controlling transport on the nanoscale［J］.Rev.Modern Phys.2009,（81）：387-443.

［3］ FEYNMAN R.P.,LEIGHTON R.B.,SANDS M.,The Feynman Lectures on Physics（Vol.I）［M］,Addison-Wesley,Reading,MA,1966,pp.46.1-46.9 （Chapter 46）.

［4］ FLACH S.,YEVTUSHENKO O.,ZOLOTARYUK Y.,Directed current due to broken time-space symmetry［J］,Phys.Rev.Lett.2000,（84）：2358-2361.

［5］ YEVTUSHENKO O.,FLACH S.,ZOLOTARYUK Y.et al.Rectification of current inac-drivennonlinearsystems andsymmetry propertiesof the Boltzmannequation［J］.Europhys.Lett.2001,（54）：141-147.

［6］ LUNDH E.,WALLIN M.,Ratchet Effect for Cold Atoms in an Optical Lattice ［J］.Phys.Rev.Lett.2005,（94）：110603-110606.

［7］ KENFACK A.,GONG J.B.,PATTANAYAK A.K.,Controlling the Ratchet Effect for Cold Atoms［J］.Phys.Rev.Lett.2008,（100）：044104-044107.

［8］ CHEN Lei,XIONG Chao,YUAN Hong-chun,et al.,A delta-kicked model for the quantum ratchet effect［J］.Physica A 2014,（398）：83-85.

［9］ RYU C.,ANDERSEN M.F.,VAZIRI A.,et al.Strongly Correlated States of Ultracold Rotating Dipolar Fermi Gases［J］.Phys.Rev.Lett.2006,（99）：160403-160406.

Study on the Evolution of the Shannon Entropy in the Double Kicked Ratchet Model

CHENLei,XIAOJin,ZHAOYu,DUWen-han
（College ofElectrical And Optical Engineering,Changzhou Institute ofTechnology,Changzhou 213002,China）

The Delta-kicked model is a Hamiltonian model of the ratchet effect.In the double ratchet ratchet model,two different frequencies of the flashing potential alternately with a uniform zero momentum initial state of particles in a，excited in the quantum resonance conditions，model appeared ratchet effect.Under different quantum resonances,the evolution of the Shannon entropy of the particles has different rules.The study shows that the quantumresonance is excited bythe analysis ofthe Shannon entropyevolution.

Double kicked ratchet model；Quantumresonance；Shannon entropy

TP211+.6

A

1674-8646（2015）12-0006-03

2015-08-17

国家自然科学基金项目（项目编号：11247323、11447002）

陈磊（1982-），男，安徽六安人，博士，讲师，主要从事量子信息与薄膜太阳能电池研究。