在数学学习中培养举一反三的能力

林琳

在数学学习中，培养创新思维能力的途径是多渠道的，有效地进行举一反三学习是培养创新思维能力的有效途径之一.举一反三能够让我们在无限的空间里实现思维的飞跃，有助于开启我们的应变力、想象力、创造力之门；举一反三以问题探究为中心，通过研究一个问题的多种解法或同一类型问题的相似解法，拓展我们思维的广度和深度；举一反三重在培养我们探究性学习的意识，激发我们的创造性学习的激情. 青少年的天性是好奇和求异，凡事喜欢问个究竟和另辟蹊径. 因此，我们要敢于求异，勇于创新.

我们都知道，数学是人类从事计量、建筑等行业必不可少的工具学科. 进入21世纪以来，社会更加需要具有探究能力和创新精神的人才，更加需要能够举一反三的人才. 因此，我们必须注重培养自己的探究能力，培养举一反三的能力，只有这样，才能适应新时代的发展，让我们在走向社会后也能继续学习.

那么如何在初中数学学习中培养自己举一反三的能力呢？

1. 成为课堂的主人

我们是课堂教学的主体，学习主要是我们自己的事情，老师只能是一个引导者和促进者. 传统教学模式中，我们习惯认为：老师讲得越多、越细、越深、越透，我们学得就越快、越好，老师带领我们探索，总比我们自己摸索要来得更快一些. 实际上，这样做容易造成我们思维的惰性. 如在学习“三角形面积”时，经常是老师演示，证明三角形等于和它等底等高的平行四边形面积的一半，使我们获得感性认识，并反复强调“等底等高”这个前提条件，从而推出三角形面积的计算公式.这种学习我们是知识的被动接受者，大大减少了我们自己思考的机会，从而使我们的思维空间越来越狭窄，不要说“反三”了，“举一”也举不好. 因为在课堂学习中，我们不需要思考，而在解答问题需要思考的时候，我们往往不知如何去思考. 我们对所要掌握的知识，没有经过自己的思考、探究，就似是而非地“知道了”，其实是一知半解，从而导致我们运用知识去理解和解答有关问题的能力不强，造成我们思维的惰性.要改变这一现状，我们就应该根据自己的体验，用自己的思维方式，自主地去探究，去发现有关的数学知识. 要做到：我们能独立思考的，不靠老师提示；我们能独立操作的，不靠老师代替；我们能独立解决的，不靠老师示范. 这样才能培养我们独立思考和“举一反三”的能力.

2. 树立正确的自信心

我们要相信自己，要相信能通过自己的努力，学好数学知识.基础较好的同学可以在“举一”的基础上“反三”甚至“反四”，中等的同学可以“反一”“反二”，基础不太好的同学把“一”举好就行了. 另外，我们可以在自由讨论中做到“生帮生”，从而促进大家的共同进步.

举一反三是培养我们创新思维能力的有效途径之一. 下面结合学习实践，谈谈在学习中诱发举一反三的几种做法.

1. 变换题设或结论

即通过对习题的题设或结论进行变换，而对同一个问题从多个角度来研究.这种训练可以增强我们解题的应变能力，培养思维的广阔性和深刻性，从而培养创新思维的品质.

2. 变换题型

即将原题重新包装成新的题型，改变单调的习题模式，从而训练我们解各种题型的综合能力，培养我们思维的适应性和灵活性，有助于我们创新思维品质的形成.

那么如何做到以上两点呢？下面以应用题为例一起探讨. 应用题是初中数学的一个重要部分，也是难点所在.

列方程解应用题一般步骤为：（1） 审题：理解题意，弄清题目中的数量关系，找出其中的相等关系；（2） 设未知数：用字母表示题目中的未知数，并用这个字母和已知数一起组成表示各数量关系的代数式；（3） 列方程；（4） 解方程；（5） 答：检查所求的解是否使方程成立，是否使实际问题有意义，写出答案.

列方程解应用题时，应根据题意灵活设未知数，一般情况下，用直接设元法设出未知数，但有时为了解题的方便，采取间接设元法；注意检验方程的解是否符合实际情况，对于不符合题意的解，一定要写明舍去的理由；注意答案的语言要明确完整，不能过于简单或省略不写.

现在就以其中常见的类型——行程问题与大家一起探讨.

1. 基本量是：路程、速度和时间.

2. 基本关系是：

3. 基本类型：相遇问题、相背问题、追及问题、行船（风速）问题、环形跑道问题等.

4. 解此类题的关键是抓住甲、乙两个对象的时间关系或所走的路程关系，一般情况下问题就能迎刃而解. 分析中还常常借助画线段图进行分析，理解行程问题.

5. 行船（风速）问题是行程问题中的一种特殊情况，其速度在不同的条件下会发生变化：

①顺水（风）速度=静水（无风）速度+水流速度（风速）；

②逆水（风）速度=静水（无风）速度-水流速度（风速）.

下面就让我们一起进入行程问题的世界：

例1 A、B两地相距1 260千米，慢车以50千米/小时的速度从A地出发，同时一列快车以70千米/小时的速度从B地出发相向而行，当两车相距60千米时，两车行驶了（ ）.

A. 9.5小时

B. 10小时

C. 11小时

D. 10小时或11小时

【分析】题中两车相距60千米，没有说明是在两车相遇前相距60千米，还是在两车相遇后背向行驶时相距60千米，所以此题有两种情况. 可以借助线段图（如图1）理清情况，并列出方程解答.

解：设当两车相距60千米时，两车行驶的时间为x小时，1 260-60=50x+70x或1 260+60=50x+70x.

得到两种情况的结果分别是10小时和11小时，答案选择D.

例2 汽车以72千米/时的速度在公路上行驶，开向寂静的山谷，驾驶员按一下喇叭，4秒后听到回声，这时汽车离山谷多远？已知空气中声音的传播速度约为340米/秒. 设听到回声时，汽车离山谷x米，根据题意，列出方程为（ ）.

A. 2x+4×20=4×340

B. 2x-4×72=4×340

C. 2x+4×72=4×340

D. 2x-4×20=4×340

【分析】此题相当于是一个相遇问题，按喇叭后汽车还在向前行驶，而声音的速度快，声音到达山谷后又“回来”与汽车“相遇”. 可以从线段图（如图2）中这样理解，在4秒的时间时，声音“所走的路程”与汽车行驶的路程总共等于汽车揿喇叭时离山谷的距离的两倍. 但这里也有要注意的地方，第一，问题中的x米是听到回声时汽车离山谷的路程；第二，条件中两个单位不统一，要化为一致后才能列方程.

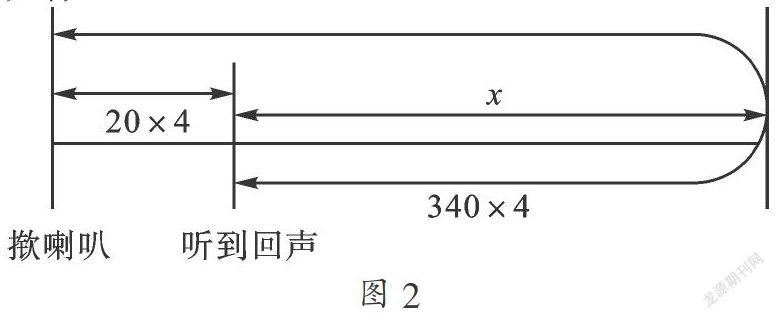
72千米/时=20米/秒.

解：设听到回声时，汽车离山谷x米.

2x=4×340-4×20.

通过比较可以得到答案应该选择A.

例3 如图1所示，两人沿着边长为90 米的正方形， 按A→B→C→D→A……的方向行走. 甲从A点以65米/分钟的速度、乙从B点以74米/分钟的速度行走，当乙第一次追上甲时，将在正方形的________边上.

【分析】此题类似于环形跑道问题，也是一个追及问题. 要充分把握好两者出发时的相距路程，追及过程中的路程与时间关系. 虽说是环正方形的行程问题，但我们也可以在线段图中体现出等量关系. 值得注意的是，本题不适合直接设，应间接设乙从出发到追上甲所用的时间为x分钟 . 求出时间后再解决问题.

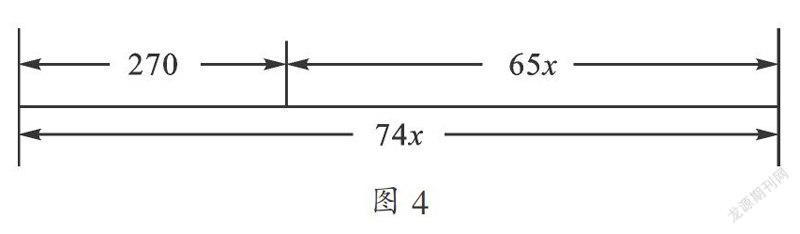
解：设乙从出发到追上甲所用时间为x分钟，

74x-65x=270，

x=30，

30×74÷360=37/6，相当于乙走了6圈多了60米，从解答可知当乙第一次追上甲时，将在正方形的BC边上.

通过以上几道例题的讲解，我们能够看出解行程问题的主要方法就是画出线段图，分析出其中的等量关系.如果同学们在解应用问题时都能找到合适的方法整理出等量关系，那么应用问题就会迎刃而解.

举一反三能够有助于开启我们的应变力、想象力、创造力之门；举一反三以问题探究为中心，通过研究一个问题的多种解法或同一类型问题的相似解法，拓展我们思维的广度和深度. 举一反三重在培养我们探究性学习的意识，激发我们的创造性学习的激情.

（作者单位：江苏省如皋市实验初级中学）